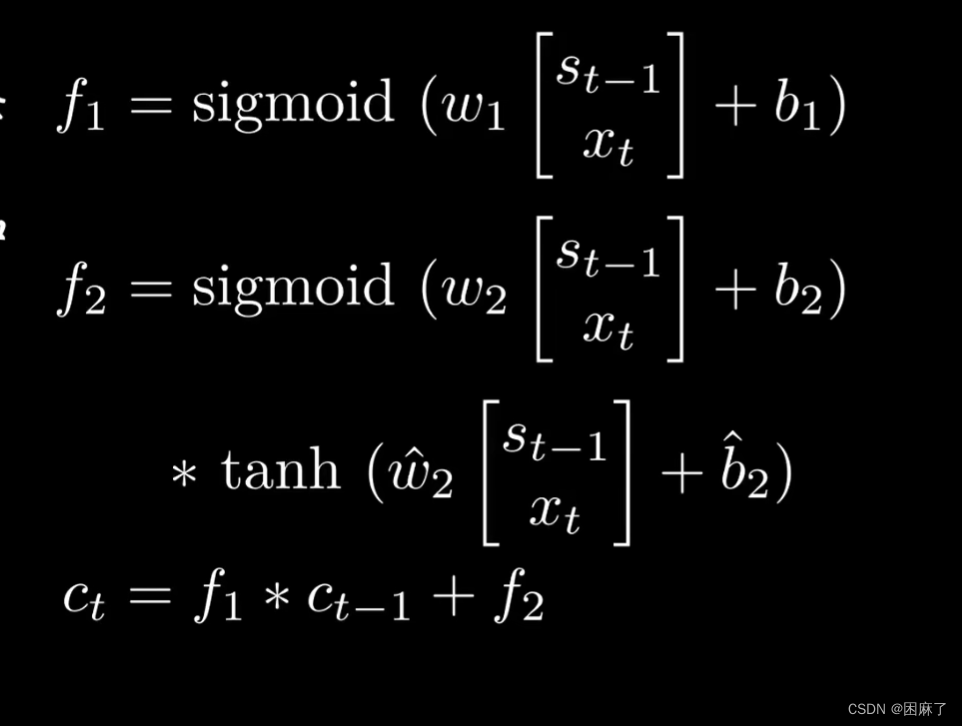给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。

每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说，如果你在 nums[i] 处，你可以跳转到任意 nums[i + j] 处:

• 0 <= j <= nums[i] 
• i + j < n

返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。

示例 1:

输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是2。
从下标为 0 跳到下标为 1 的位置，跳1步，然后跳3步到达数组的最后一个位置。

示例 2:

输入: nums = [2,3,0,1,4]
输出: 2

提示:

• 1 <= nums.length <=
• 0 <= nums[i] <= 1000
• 题目保证可以到达 nums[n-1]

---

分解题目：

• 目标：求解跳到最后一个位置的最小跳跃数
• 依赖于：存在一个位置能跳到最后一个位置（题目已经保证此项）
                跳到这个位置的最小跳跃数。
• 如果用 i 来表示最后一次跳跃，i - 1表示的倒数第二次跳跃，很明显，求解 i 的最小跳跃数可以转换为求解 i - 1的最小跳跃数。

至此，可以用动态规划进行解决。

定义：dp[ i ]表示跳跃到第 i 个位置的最小跳跃数。dp[n - 1]即为所求，边界值dp[0] = 0。

对于第 i 个位置，可能有多个前置的位置可以跳跃到达，我们需要找到其中的最小值，即：

j from 0 to i
if(nums[j]+j>i)  dp[i]=min(dp[i],dp[j]+1); 

完整代码：

class Solution {
public:
    int jump(vector<int>& nums) {
        int n = nums.size();
        vector<int> dp(n,n);
        dp[0] = 0;
        for(int i = 1;i < n;++i){
            for(int j = 0; j < i;++j){
                if(nums[j] + j >= i){
                    dp[i] = min(dp[i],dp[j] + 1);
                }
            } 
        }
        return dp[n-1];
    }
};

然而这里的动态规划反而引入了更多的重复计算。

如果换成贪心算法：

class Solution {
public:
    int jump(vector<int>& nums) {
        int jumps = 0;
        int end = 0;
        int farthest = 0;
        for (int i = 0; i < nums.size() - 1; i++) {
            farthest = max(farthest, nums[i] + i);
            if (i == end) {
                jumps++;
                end = farthest;
                if (end >= nums.size() - 1) {
                    break;
                }
            }
        }
    return jumps;
    }
};

• jumps是跳跃的次数，end是当前的终点，farthest是当前点跳跃能够到达的最远点。
• 遍历数组，除了最后一个元素，因为最后一个元素的位置不需要跳跃，自己就能到达自己。
• 我们时刻维护从当前点到达的最远距离，当我们到达了当前终点，就把最远距离设置成终点，这里体现贪心的思想。
• 同时，当到达了end时，也说明需要进行一次跳跃。

即：每次在上次能跳到的范围（i，end）内选择一个能跳的最远的位置（也就是能跳到farthest位置的点）作为下次的起跳点。

对于初学者，这看上去非常的反直觉，这是不是局部最优？为什么是全局最优？如果出现当前跳的最远，但是下下步跳得近了怎么办？

这里需要理解end的作用，如果把end抽象成一个分隔符，所谓跳跃过程就是在数组内插入分隔符的过程，使最终分出的子数组数量最小。

而fareset的作用是，保留上一个end到当前end这个区间范围内可以达到的最远值。

注意区间范围这个点。

在贪心算法中，每一步的end都是当前范围能到达的最远点，也即最大值farest，所以最终分出的间隔就会更少。

下面用一个具体图例做进一步解释，初始状态，进行第一次跳跃：

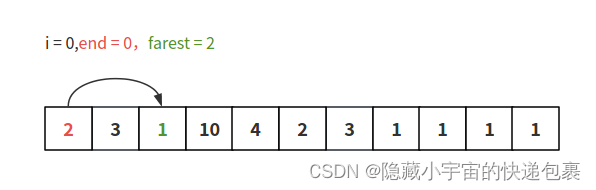
 跳跃后在区间内遍历维护最远值farest：

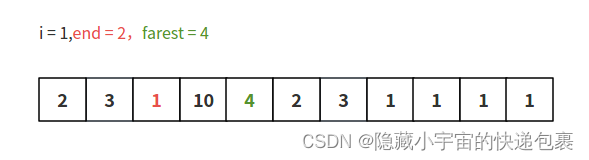
这里有人可能会说，看起来像恰好1就跳到了较大值10。那如果我们把这里的1换成0会发生什么？

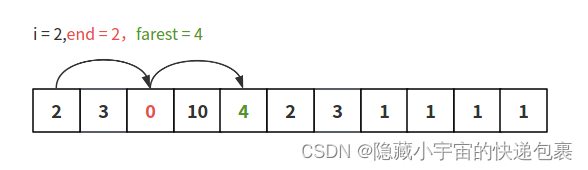
可以看到维护的farest，才是起到关键作用的值。和nums[end]中的值并无全部关系。 这也是上面提到的，保留上一个end到当前end这个区间范围内可以达到的最远值。

图中箭头描述的是end变化的过程，真实的跳跃过程和end的变化过程数量相同，但是路径不一定相同。（每条end箭头仅对应一条跳跃，比如这里是从2跳到3跳到10。）

继续遍历：

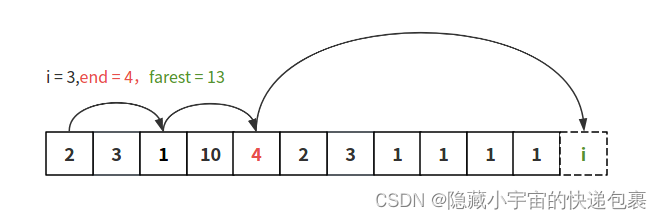
只要理解了end表示间隔且和真实跳跃一一对应，farest表示一个区间内跳到的最远距离这两个概念，这里的贪心算法就很好理解了。