RNN
RNN简介
我们来看一看百度百科给的解释
下面是循环神经网络的一部分
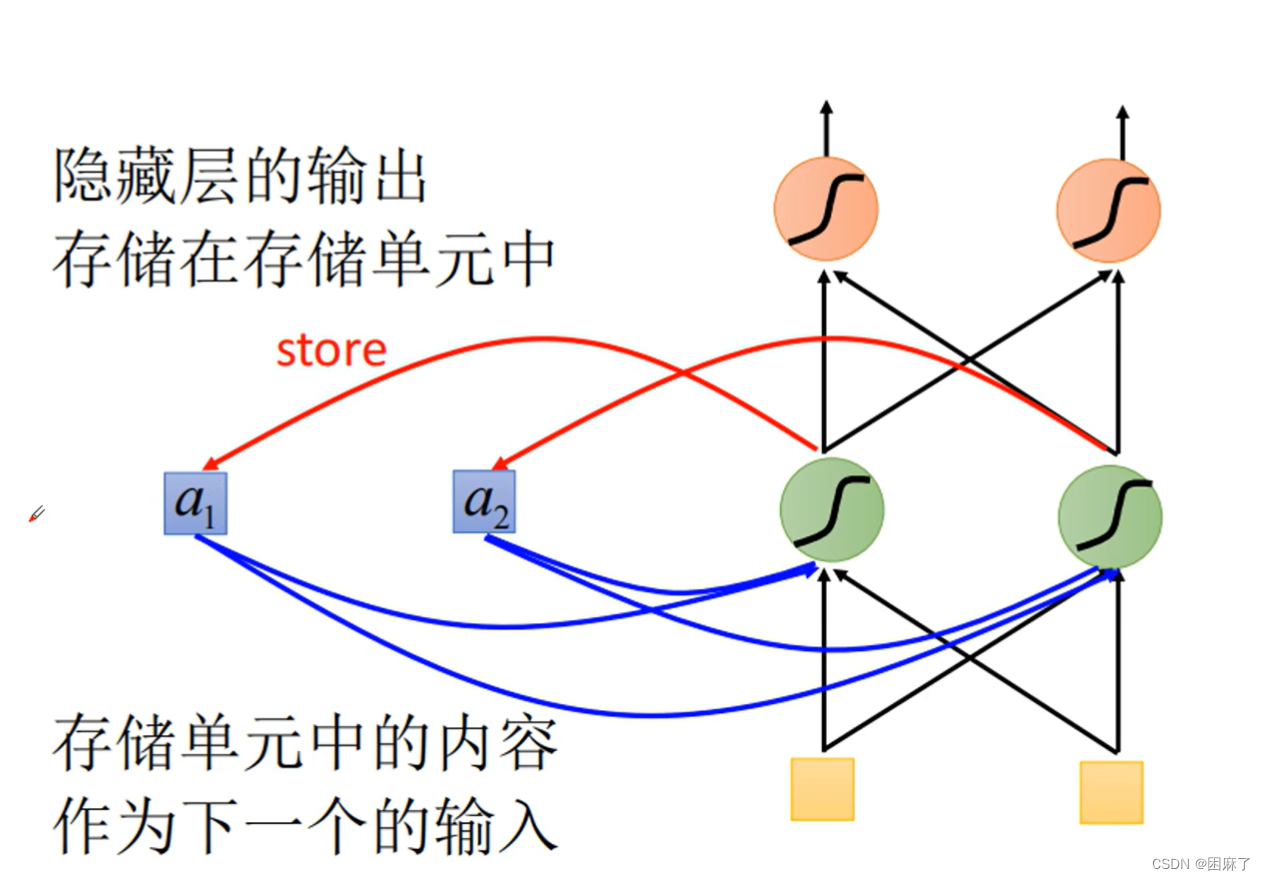
黑色直线代表权重，a1，a2代表存储单元，黄色框框代表输入，曲线是激活函数
RNN常用领域
- 语言建模（Language Modeling）：RNN可以根据前文预测下一个单词或字符，用于自动文本生成、拼写纠错等任务。
- 机器翻译（Machine Translation）：RNN可以将输入语言的序列转换为输出语言的序列，实现自动翻译。
- 文本分类（Text Classification）：RNN可以对文本进行情感分析、垃圾邮件过滤等分类任务。
- 命名实体识别（Named Entity Recognition）：RNN可以识别文本中的人名、地名、组织名等实体。
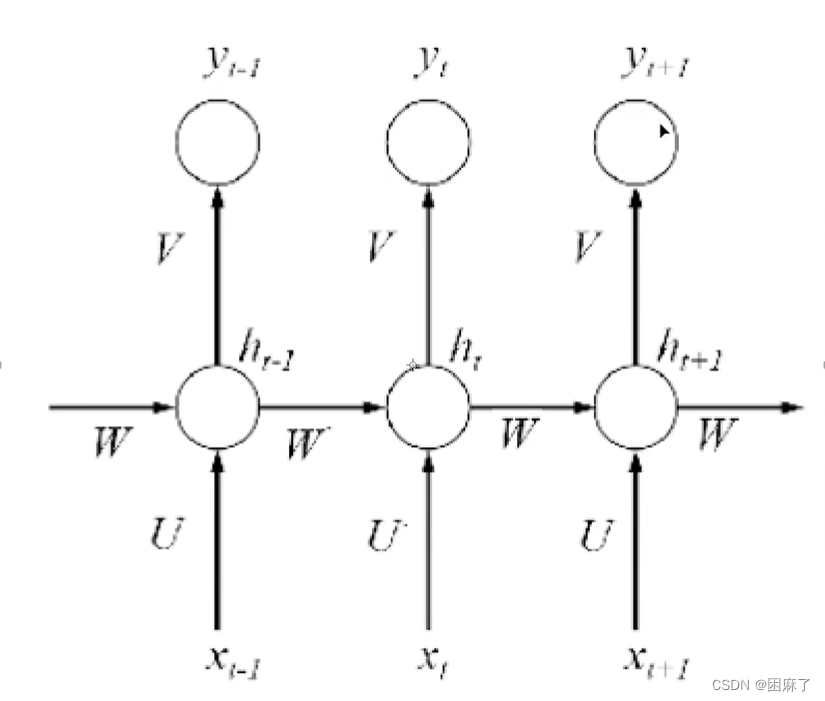
RNN结构
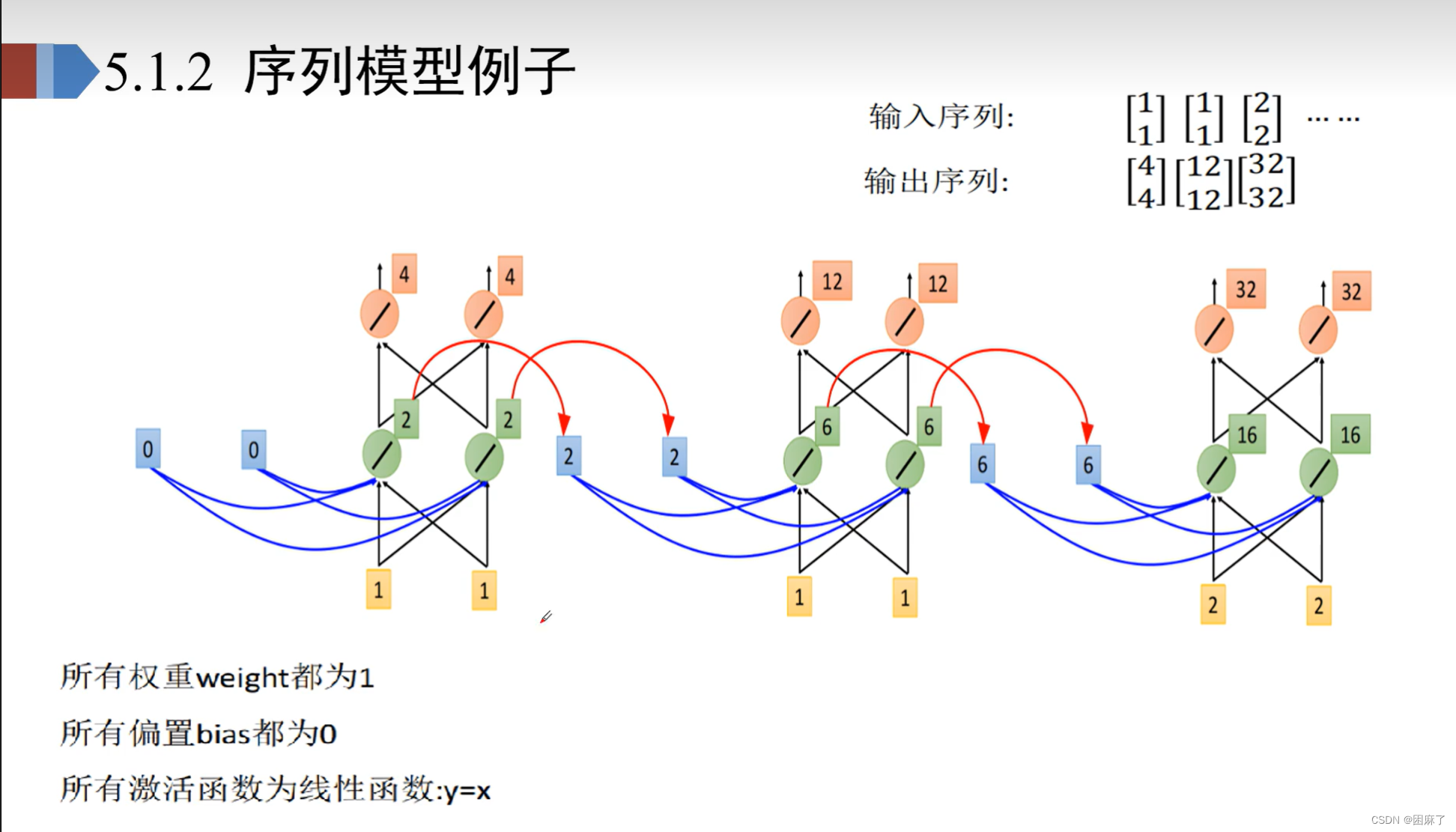
这是一个序列模型的例子。
我们可以看出， 这个是模型是由很多个相同的网络结构结成的，因此也称它为循环神经网络。
我们将这个网络的结构进行抽象，然后展开，就得到了以下内容：
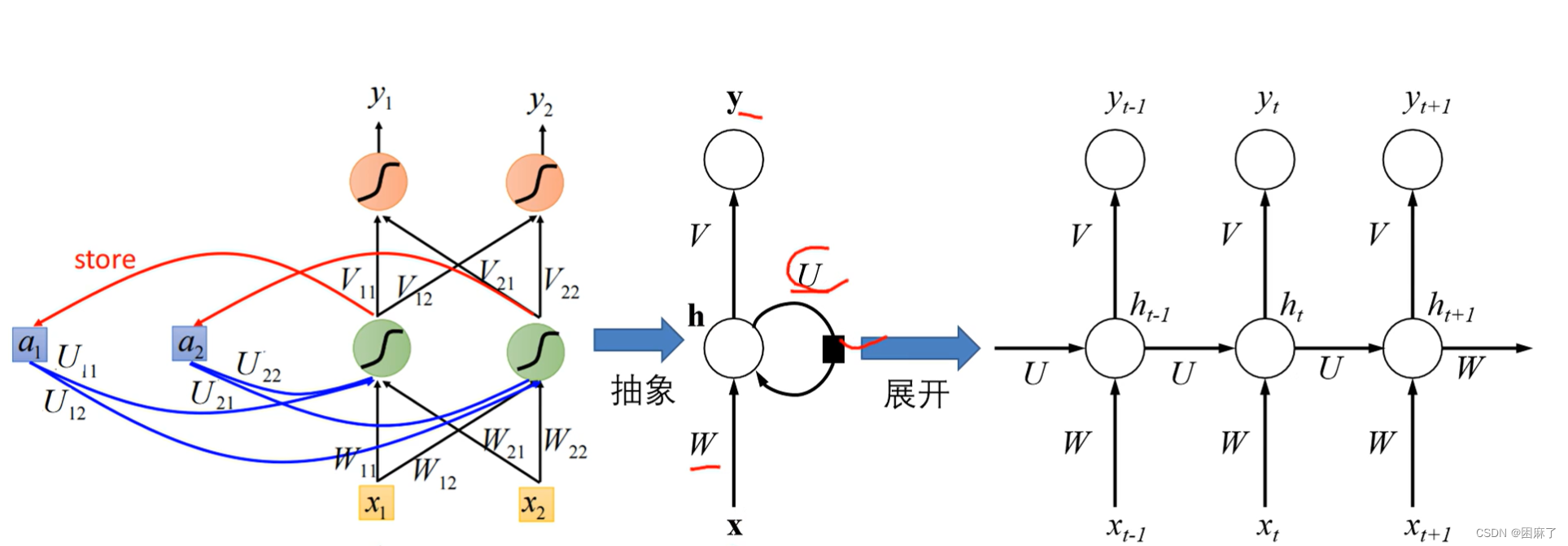
RNN的工作原理
循环神经网络的工程原理其实就是它的训练算法，一种基于时间的反向传播算法BPTT.
BPTT算法是针对循环层设计的训练算法，它的工作原理和反向传播BP的工作原理是相同的，也包含同样的三个步骤:
1.前向计算每个神经元的输出值。
2.反向计算每个神经元的误差项值，它是误差函数对神经元的加权输入的偏导数。
3.计算每个权重的梯度，用随机梯度下降法更新权重。
以下是加权输入的含义：
现在，我们就对RNN有了大致的了解，下面就让我们来具体学习它的各个部分的内容。
RNN的前向传播
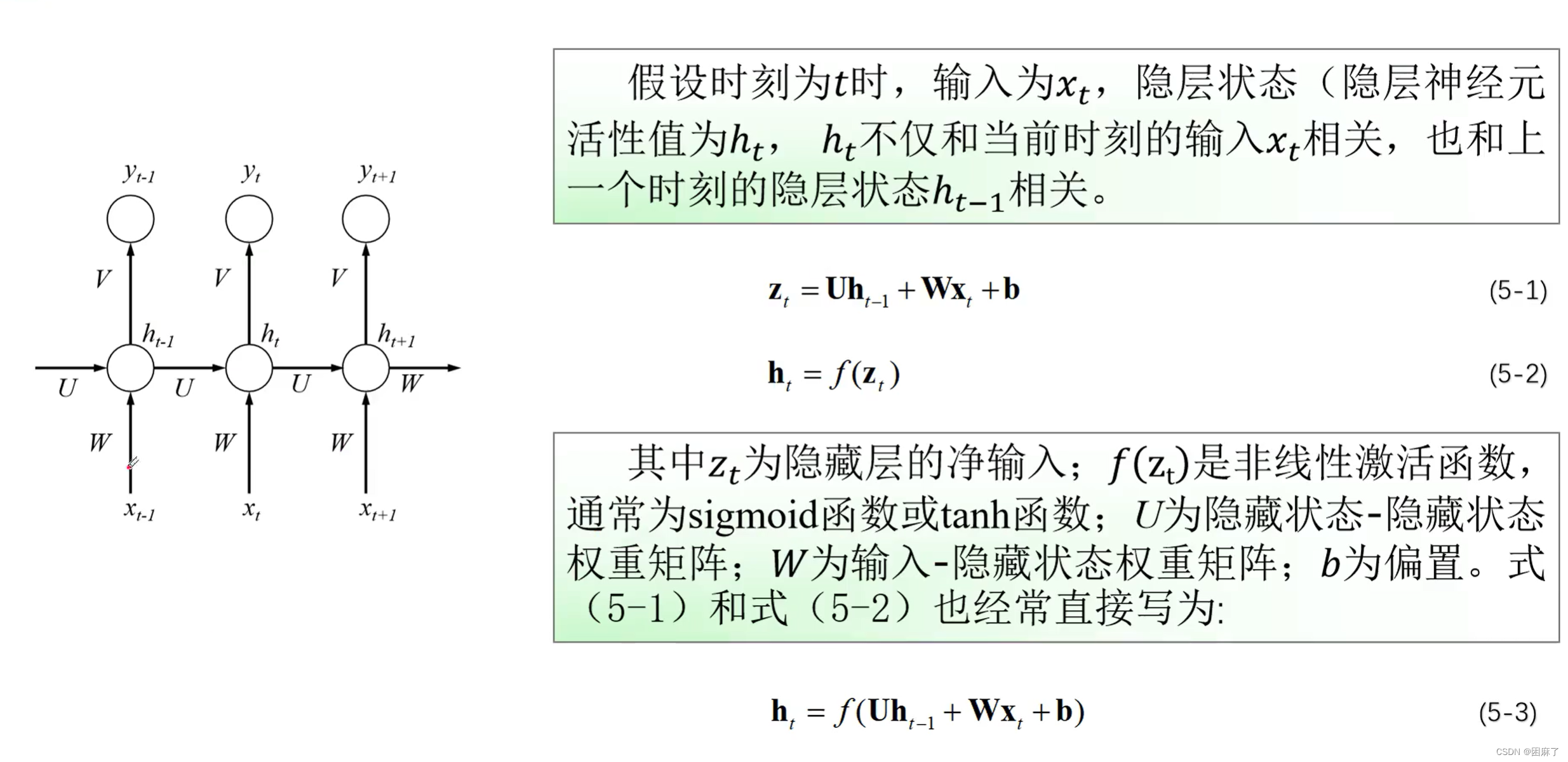
我们主要观察中间那层，b我们设为0，可以忽略不计
中间结果z=前一层即隐藏层的值*隐藏层权重U+这一层的输入值*权重W
我们对z加上激活函数得到h，我们这在这里用到的是Tanh激活函数
这是隐藏层中间结果的表示方法。
输出层y的表示方法。
V在这里表示的也是权重。
g()是使用Softmax激活函数。
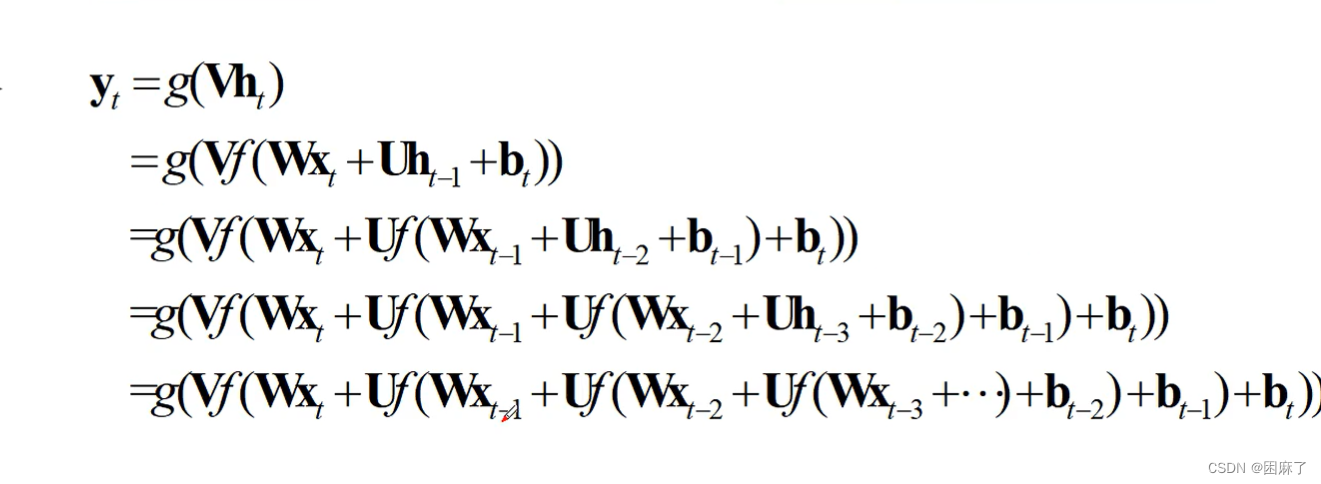
这是我们的输出值的最终函数，也就是一个嵌套的循环函数。
接下来，我们对应公式来书写代码
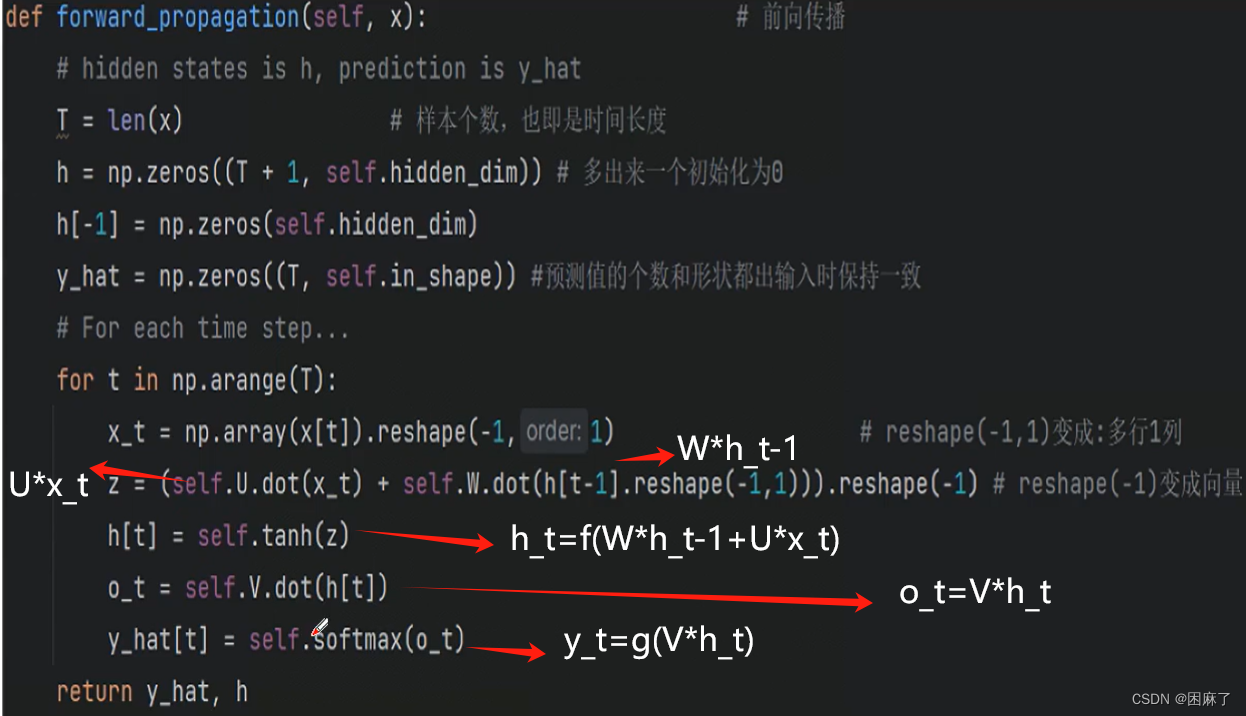
代码
import numpy as np
def forward_propagation(self,x):
T=len(x) # T为输入序列的长度
# 初始化
h=np.zeros((T+1,self.hidden_dim))
h[-1]=np.zeros(self.hidden_dim)
y_pre=np.zeros((T,self.in_shape))
for t in np.arange(T):
x_t=np.array(x[t]).reshape(-1,1)
z=(self.U.dot(x_t)+self.W.dot(h[t-1].reshape(-1,1))).reshape(-1)
h[t]=self.tanh(z)
o_t=self.V.dot(h[t])
y_pre[t]=self.softmax(o_t)
return y_pre,hRNN的后向传播
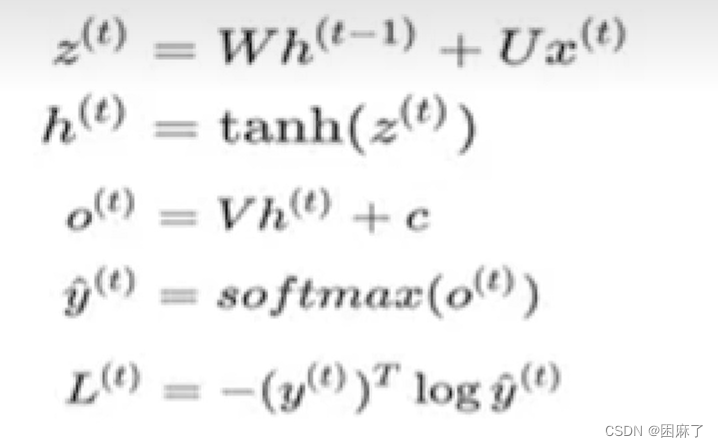
这是我们的公式。
最后的L_t是对预测值求交叉熵损失函数，是一个标量。
c为偏置，不存在的话可以不写。
我们先要了解两部分知识：
必备知识
标量对多个矩阵的链式求导法则
要注意的是，这里要进行转置。
标量对多个向量的链式求导法则
z为标量，x为向量
对权重的求导
对V求导
对W求导
我们可以对照公式进行理解。
第一部分
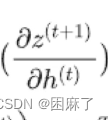这一部分如下
因为
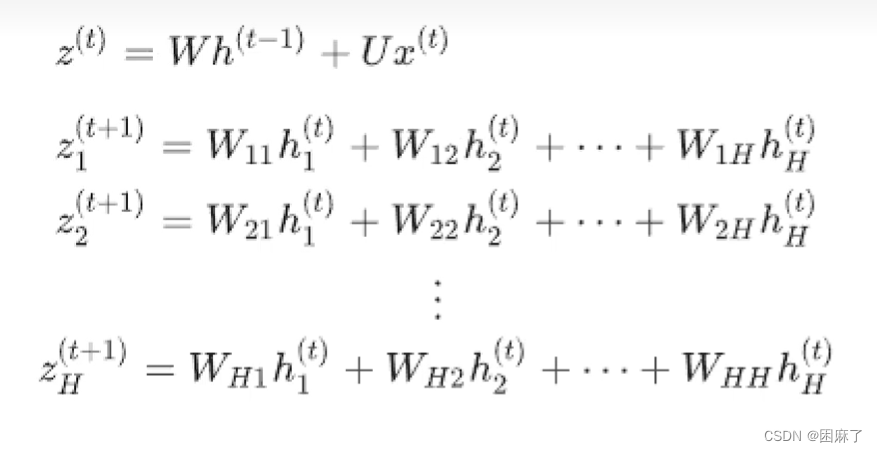
所以就有了
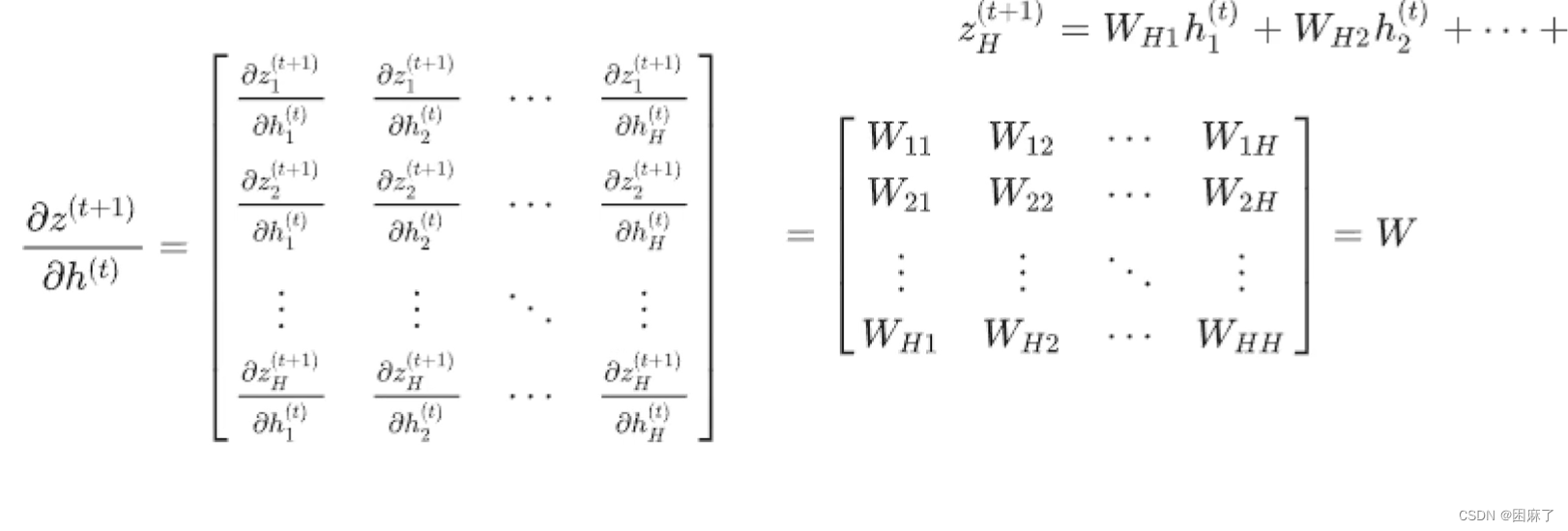
第二部分
然后是下一个部分
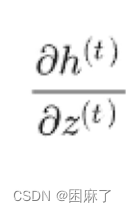它是怎么求的呢？
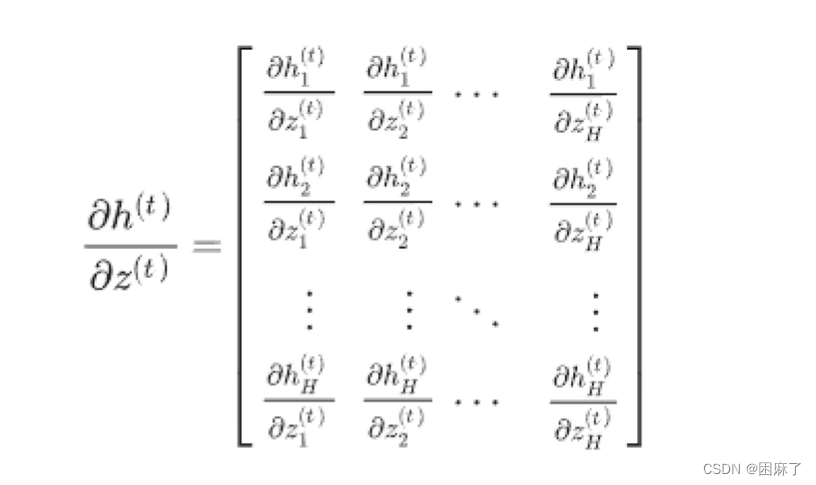
因为h1只和z1有关，h2只和z2有关，所以上面变为了对角矩阵：
第三部分
这一部分：
我们先要知道tanh的求导公式：
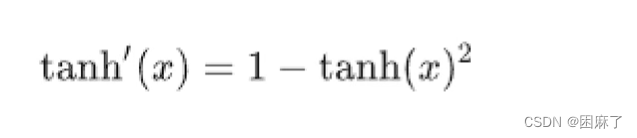
然后我们就得到了以下结果
对U求导
与对W求导是一样的
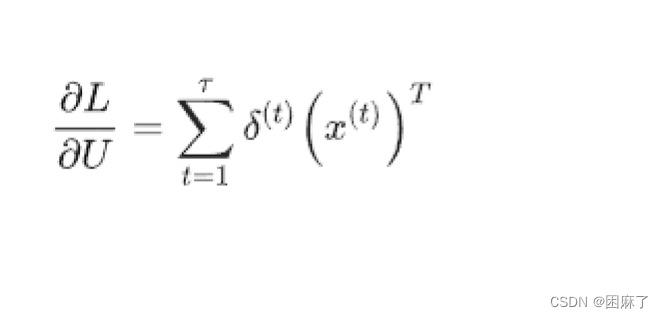
RNN的梯度更新
通过后向传播，我们可以得到以下公式：
既然我们得到了公式，我们就可以写出相对应的代码了：
这里是用纯python写的
import torch
import numpy as np
class RNN(torch.nn.Module):
def __init__(self,input_size,output_size,hidden_dim,n_layers):
super(RNN,self).__init__()
self.hidden_dim = hidden_dim
self.n_layers = n_layers
self.rnn = torch.nn.RNN(input_size,hidden_dim,n_layers,batch_first=True)
self.linear=torch.nn.Linear(hidden_dim,output_size)
def forward(self,x):
batch_size = x.size(0)
hidden= torch.zeros(self.n_layers,batch_size,self.hidden_dim)
out,hidden=self.rnn(x,hidden)
out = self.linear(out)
return out,hidden我们在这里简单了解一下就好了，。
RNN的pythorch框架代码实现
在这里，我们需要先了解一些函数
torch.nn.RNN
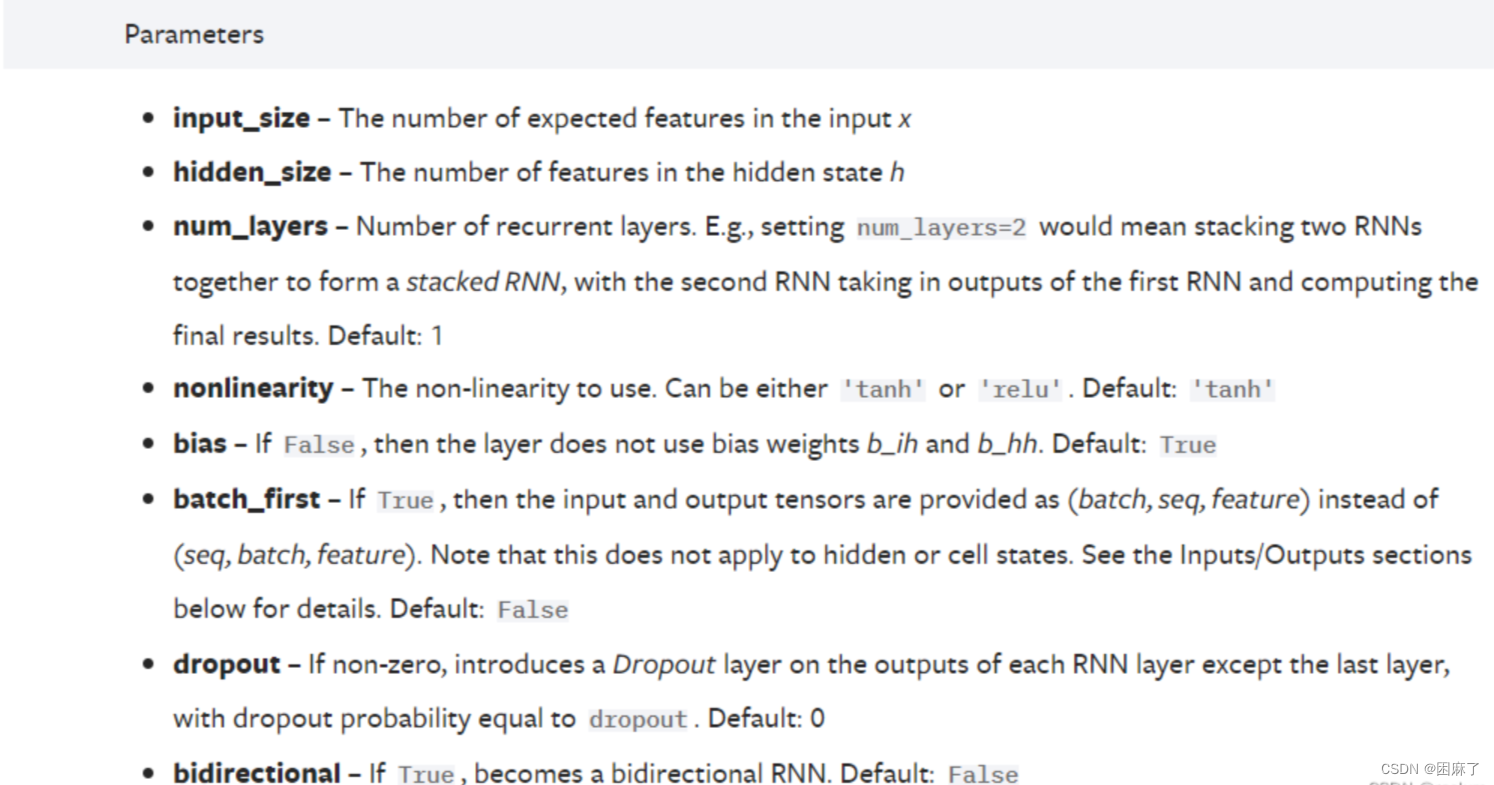
参数说明
input_size：即 d ；
hidden_size：即 h ；
num_layers：即RNN的层数。默认是 1 层。该参数大于 1 时，会形成 Stacked RNN，又称多层RNN或深度RNN；
nonlinearity：即非线性激活函数。可以选择 tanh 或 relu，默认是 tanh；
bias：即偏置。默认启用，可以选择关闭；
batch_first：即是否选择让 batch_size 作为输入的形状中的第一个参数。当 batch_first=True 时，输入应具有 N × L × d这样的形状，否则应具有 L × N × d 这样的形状。默认是 False；
dropout：即是否启用 dropout。如要启用，则应设置 dropout 的概率，此时除最后一层外，RNN的每一层后面都会加上一个dropout层。默认是 0 ，即不启用；
bidirectional：即是否启用双向RNN，默认关闭。
torch.nn.Linear
torch.nn.Linear(in_features, # 输入的神经元个数
out_features, # 输出神经元个数
bias=True # 是否包含偏置
)
实际上，他进行的是y_pre=w*x+b的线性变换，从而得到预测值y_pre。
torch.zeros
torch.zeros(
*sizes, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False
)
参数说明
*sizes：一个或多个整数，用于指定张量的形状（shape）。可以传递多个参数来创建一个多维张量。
out：可选参数，用于指定输出张量的位置。
dtype：可选参数，用于指定输出张量的数据类型。默认为 None，表示使用默认数据类型。
layout：可选参数，用于指定张量的布局。默认为 torch.strided。
device：可选参数，用于指定张量的设备（CPU 或 GPU）。
requires_grad：可选参数，指示是否为张量启用梯度计算。默认为 False。
代码
在这里，我们仍需对照图像进行理解
import torch
import numpy as np
class RNN(torch.nn.Module):
def __init__(self,input_size,output_size,hidden_dim,n_layers):
super(RNN,self).__init__()
self.hidden_dim = hidden_dim
self.n_layers = n_layers
self.rnn = torch.nn.RNN(input_size,hidden_dim,n_layers,batch_first=True)
self.linear=torch.nn.Linear(hidden_dim,output_size)
def forward(self,x):
batch_size = x.size(0)
hidden= torch.zeros(self.n_layers,batch_size,self.hidden_dim)
out,hidden=self.rnn(x,hidden)
out = self.linear(out)
return out,hidden在前向传播中，
batch_size=x.size(0) 这行代码获取输入张量x的第一个维度的大小;
在这里，hidden是形状为（
self.n_layers,batch_size,self.hidden_dim
）的全零张量
RNN的缺点：梯度爆炸和梯度消失
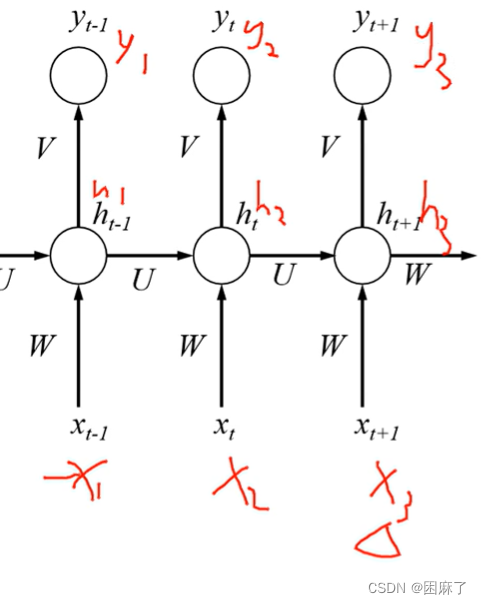
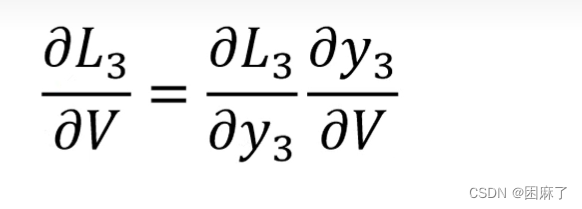
L3是第三个时间点的交叉熵损失函数
在这里我们是L3对V求偏导，通过图像我们可以得到上面的结果，然后再通过结果可以看出，对V求偏导并没有长期依赖。
我们再来看下面的对U和W求偏导
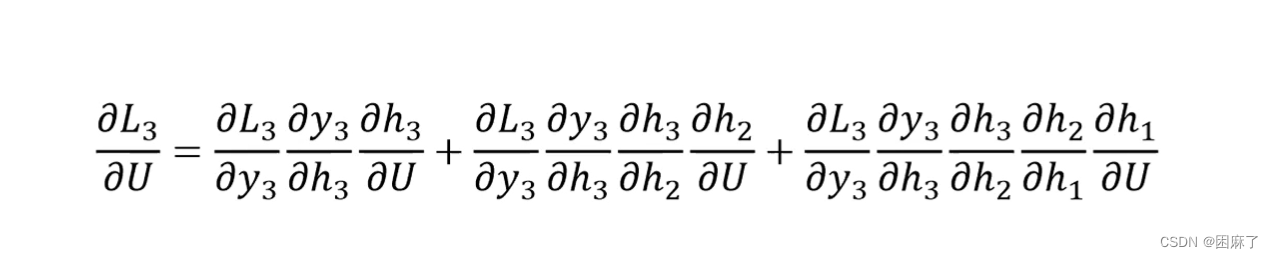
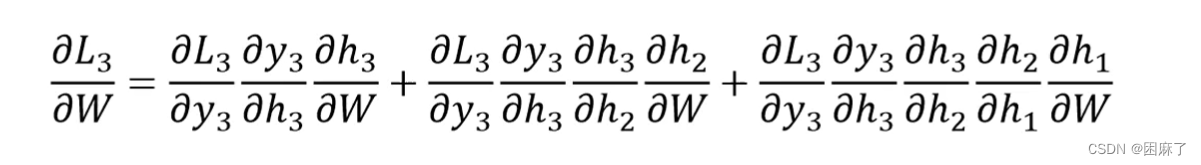
推导过程上面已经提到了，这里就不多说了。
我们可以看出，对U和W求偏导的式子都特别长，对它们求偏导会随着时间序列产生长期依赖
我们可以把上面的式子写成下面的形式：
然后再加上激活函数
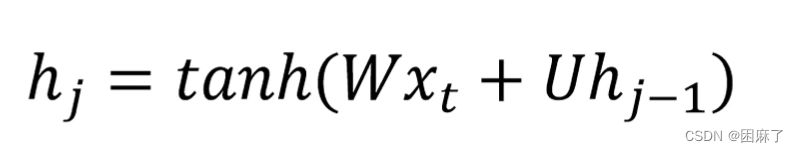最终得到
下面是f(x)=tanh部分的图像
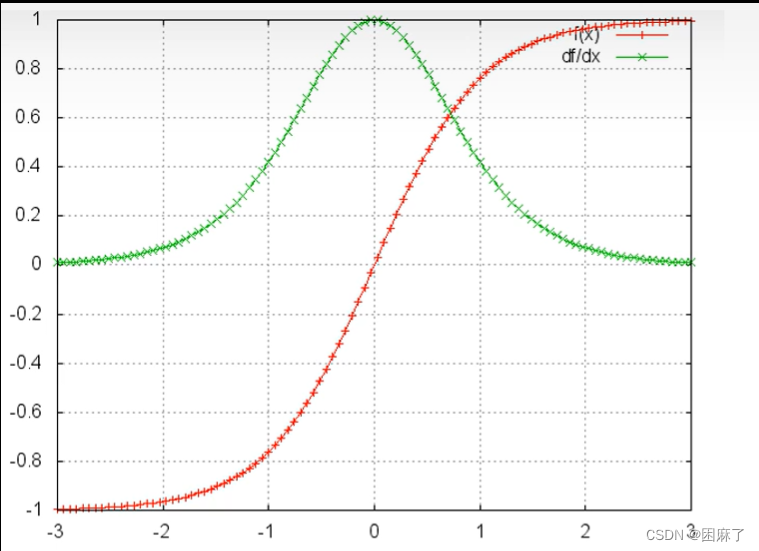
通过上面这张图片，我们可以得到 f（x）的导数的值域是在0到1之间的。
训练过程中，大部分情况tanh的导数都是小于1的，那么如果U也是一个大于0小于1的值，当t很大即时间序列很大时，梯度值就会趋近于0，造成 ；
同理，当U很大时，梯度时就会趋近于无穷，造成梯度爆炸。
那么RNN怎么解决梯度爆炸和梯度消失呢，就是用到了LSTM
LSTM
前向传播
这里的
指的是进行了Sigmoid激活函数
我们可以把图和公式对应起来，进行理解
反向传播
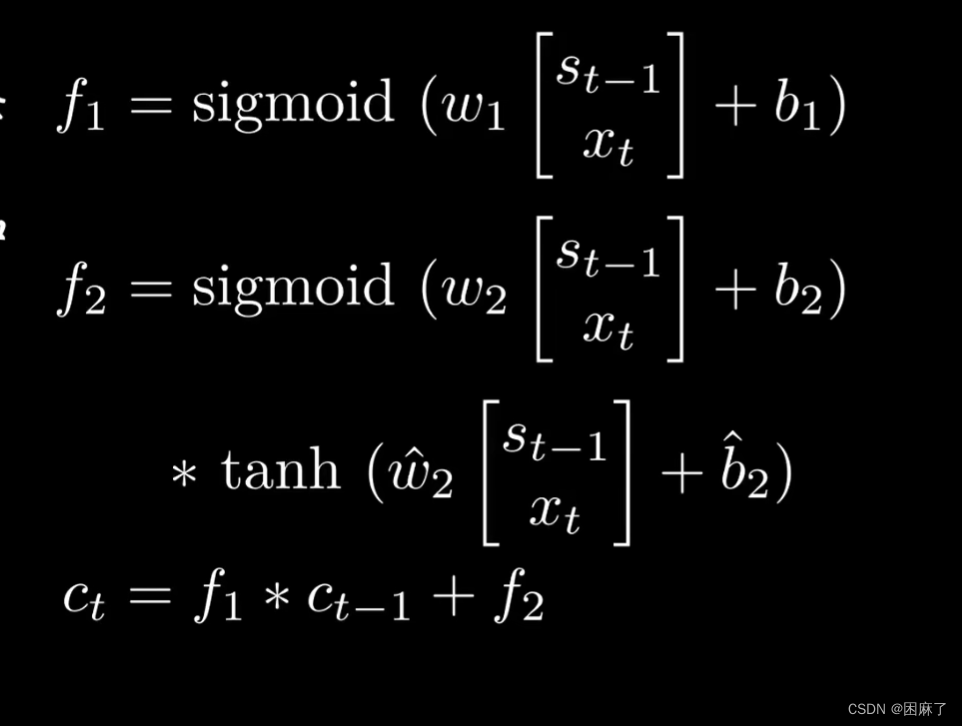在这里，f1是指遗忘门的内容，f2是指输入门，ct表示新的记录，而ct-1就表示上一条记录。
f1，遗忘门，我们这里可以理解为橡皮，对f1进行sigmoid,相当于把不重要的信息删除掉，保留重要的信息。
f2，输入门，我们可以理解为铅笔，同样进行sigmoid后，再*tanh，相当于对所有信息进行一个梳理
pytorch代码
import torch
import numpy as np
class LSTM(torch.nn.Module):
def __init__(self, input_size, hidden_dim, output_size,n_layers):
super(LSTM, self).__init__()
self.input_size = input_size
self.hidden_size = hidden_dim
self.output_size = output_size
self.n_layers = n_layers
self.lstm = torch.nn.LSTM(input_size, hidden_dim, n_layers, batch_first=True)
self.fc = torch.nn.Linear(hidden_dim, output_size)
def forward(self,x):
h0=torch.zeros(self.x.size(0), self.n_layers,self.hidden_size).to(x.device)
c0 = torch.zeros(self.x.size(0), self.n_layers, self.hidden_size).to(x.device)
out,hidden=self.lstm(x,(h0,c0))
out = self.fc(out[:,-1,:])
return out,hidden在LSTM模型中，最核心的部分也就是前向传播的部分了。
核心代码解析
h0=torch.zeros(self.x.size(0), self.n_layers,self.hidden_size).to(x.device) c0 = torch.zeros(self.x.size(0), self.n_layers, self.hidden_size).to(x.device)
需要注意的是，在上面的__init__中，由于我们将batch_first设为Ture，输入和输出的张量的形状就是(batch, seq_len, input_size)，
其中batch是批处理大小，seq_len是序列长度，我们在这里用的是n_layers，input_size是特征维度。
如果batch_first=False（默认值），则输入张量的形状为(seq_len, batch, input_size)。
所以，在zeros中，传入的参数依次为 self.x.size(1), self.n_layers,self.hidden_size
由于 batch_first=True，batch 的大小就是张量的第一个维度 ，也就是 x.size(0)
最后面的 to(x.device)用来确保这些张量位于与输入张量x相同的设备上（例如，CPU或GPU）
out = self.fc(out[:,-1,:])
在这里我们用到了一个截取的操作
python矩阵的切片（或截取）-CSDN博客
我们可以通过这个文章来复习一下。
这是指在最后的结果中，我们截取每个样本（第一个维度）中的最后一个时间步（-1）的所有特征（第三个维度）。
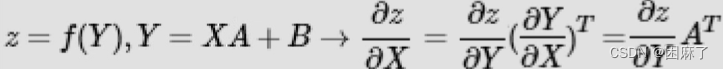
![[iOS]CocoaPods安装和使用](https://img-blog.csdnimg.cn/direct/cc42417e4af84707b6741df16c17fe91.png)
