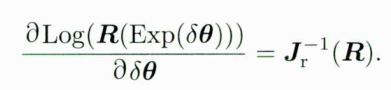IMU&GNSS的误差状态卡尔曼滤波器(ESKF)---更新过程
- ESKF的更新过程
ESKF的更新过程
前面介绍的是ESKF的运动过程,现在考虑更新过程。假设一个抽象的传感器能够对状态变量产生观测,其观测方程为抽象的h,那么可以写为
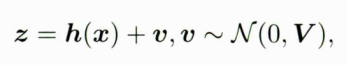
其中z为观测数据,v为观测噪声,V为该噪声的协方差矩阵。
在传统的EKF中,可以直观地对观测方程线性化,求出观测方程相对与状态变量的雅克比矩阵,进而更新卡尔曼滤波器。而在ESKF中,当前拥有名义状态变量x的估计和误差状态变量delta x的估计,且希望更新的是误差状态,因此要计算观测方程相对于误差状态的雅克比矩阵:
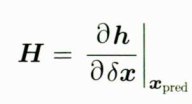
然后计算卡尔曼增益,进而计算误差状态的更新过程:
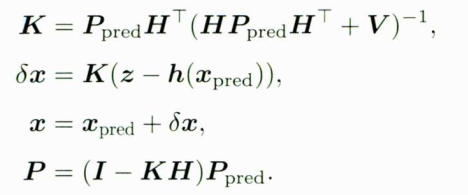
其中,K为卡尔曼增益,Ppred为预测的协方差矩阵,最后的P为修正后的协方差矩阵。
下面就是如何计算H,大部分的观测数据是对名义状态的观测。此时H可以通过链式法则来生成:
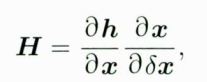
其中第一项只需对观测方程进行线性化;第二项,根据之前对状态变量的定义,可以得到
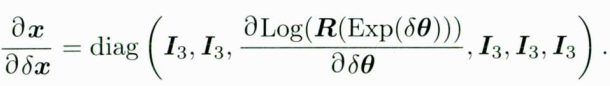
其它几项都是平凡的,只有旋转部分,因为 delat theat 定义为R的右乘,用右乘的BCH即可