一、SlidingWindowMaximum(滑动窗口最大值)
前置题,155.最小栈
参考K神155. 最小栈 - 力扣(LeetCode)
做完最小栈的题能更好的理解这道题
鄙人想到了开辟空间来保存最小值,使用的HashMap;K神用的是栈+逻辑优化
class MinStack {
private Stack<Integer> stack;
private Stack<Integer> min_stack;
public MinStack() {
stack = new Stack<>();
min_stack = new Stack<>();
}
public void push(int val) {
stack.push(val);
if (min_stack.isEmpty() || val <= min_stack.peek())
min_stack.push(val);
}
public void pop() {
if (stack.pop().equals(min_stack.peek()))
min_stack.pop();
}
public int top() {
return stack.peek();
}
public int getMin() {
return min_stack.peek();
}
}
参考239. 滑动窗口最大值 - 力扣(LeetCode)
- 使用双端队列保存每个窗口的最大值
- 左指针 > 0,也就是左指针 "存在"的时候,每次滑动窗口都要将队列第一个元素删除,保持和窗口一致
- 右指针在添加新元素的时候会判断队列中所有元素是否小于该元素,小于的部分将被删除
- 如果队列中所有元素都小于该新增元素,那么新增元素就是最大的元素
- 如果队列中存在元素 >= 该新增元素,停止移除元素,push该元素,我们会发现这个队列是 非严格递减(单调不增),与最小栈压辅助栈是相同的原理
- 单调不增,不递增 -> 有两种可能,递减或相等
滑动窗口不分阶段
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
if(nums.length == 0 || k == 0) return new int[0];
Deque<Integer> deque = new LinkedList<>();
int[] res = new int[nums.length - k + 1];
//左指针i,右指针j,为了保证每次循环的条件相同(即Carl哥讲的循环不变量),这里我们发现K写的代码右指针是从0开始遍历的,而左指针则是 0 - (k - 1) = 1 - k开始遍历的
for(int j = 0, i = 1 - k; j < nums.length; i++, j++) {
// 删除 deque 中对应的 nums[i-1]
if(i > 0 && deque.peekFirst() == nums[i - 1])
deque.removeFirst();
// 保持 deque 递减,
// 循环停止 1.deque为空,表示nums[j]是当前最大的值,deque最后剩一个值
// 2.deque.peekLast() >= nums[j],表示小于等于deque中的剩余元素
while(!deque.isEmpty() && deque.peekLast() < nums[j])
deque.removeLast();
deque.addLast(nums[j]);
// 记录窗口最大值
if(i >= 0)
res[i] = deque.peekFirst();
}
return res;
}
}
滑动窗口分阶段
- 因为不分阶段时左指针的起始索引为 1-K < 0 ,没在数组区间内,因此没形成窗口
- 当左指针 >= 0 时,窗口就在数组中了,即已经形成窗口
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
if(nums.length == 0 || k == 0) return new int[0];
Deque<Integer> deque = new LinkedList<>();
int[] res = new int[nums.length - k + 1];
// 未形成窗口
for(int i = 0; i < k; i++) {
while(!deque.isEmpty() && deque.peekLast() < nums[i])
deque.removeLast();
deque.addLast(nums[i]);
}
res[0] = deque.peekFirst();
// 形成窗口后
for(int i = k; i < nums.length; i++) {
// i = k,i此时是右指针,左指针为0,右指针为 k - 1
//i = k 为新的右指针,原左指针为 i - k(多减了一个1),如果原左指针等于队列中最大值,则将队列中最大值删除(这步是判断被移除的元素是否是原来的窗口的最大值)
if(deque.peekFirst() == nums[i - k])
deque.removeFirst();
//保持 deque 递减
while(!deque.isEmpty() && deque.peekLast() < nums[i])
deque.removeLast();
deque.addLast(nums[i]);
// i - (k - 1) 是当前的左指针
res[i - k + 1] = deque.peekFirst();
}
return res;
}
}
二、前K个高频元素
前置知识:
简单写一下堆的知识,便于理解优先队列,已经了解的朋友转到逻辑部分
参考8.1 堆 - Hello 算法 (hello-algo.com)
-
堆:是一种满足特定条件的完全二叉树,主要可分为两种类型
- 小顶堆(min heap):任意节点的值 ≤ 其子节点的值。
- 大顶堆(max heap):任意节点的值 ≥ 其子节点的值。
-
堆作为完全二叉树的一个特例,具有以下特性。
- 最底层节点靠左填充,其他层的节点都被填满。
- 我们将二叉树的根节点称为“堆顶”,将底层最靠右的节点称为“堆底”。
- 对于大顶堆(小顶堆),堆顶元素(根节点)的值是最大(最小)的。
实际上,堆通常用于实现优先队列,大顶堆相当于元素按从大到小的顺序出队的优先队列。从使用角度来看,我们可以将“优先队列”和“堆”看作等价的数据结构。
-
堆的存储与表示
- “二叉树”章节讲过,完全二叉树非常适合用数组来表示。由于堆正是一种完全二叉树,因此我们将采用数组来存储堆。
- 当使用数组表示二叉树时,元素代表节点值,索引代表节点在二叉树中的位置。节点指针通过索引映射公式来实现。
- 给定索引 i ,其左子节点的索引为 2i+1 ,右子节点的索引为 2i+2 ,父节点的索引为 (i−1)/2(向下整除)。当索引越界时,表示空节点或节点不存在。如图
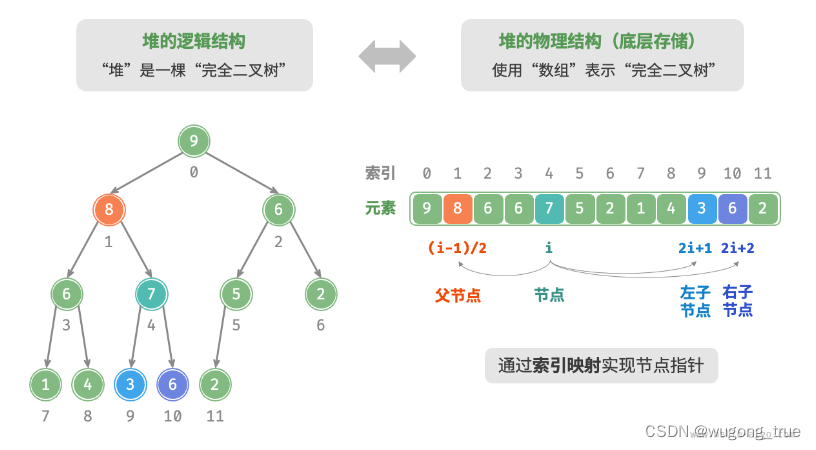
-
建堆操作
- 借助入堆操作实现,设元素数量为 n ,每个元素的入堆操作使用 n(logn) 时间,因此该建堆方法的时间复杂度为时间复杂度O(nlogn)
- 通过遍历堆化实现
- 将列表原封不动添加到堆当中,此时还没有满足堆的性质
- 倒序遍历堆(层序遍历的倒序),依次对每个非叶节点执行“从顶至底堆化”。
- 复杂度
- 假设完全二叉树的节点数量为 n ,则叶节点数量为 (n+1)/2 ,其中 / 为向下整除。因此需要堆化的节点数量为 (n−1)/2 。
- 在从顶至底堆化的过程中,每个节点最多堆化到叶节点,因此最大迭代次数为二叉树高度 logn。
- 将上述两者相乘,可得到建堆过程的时间复杂度为O(nlogn) 。但这个估算结果并不准确,因为我们没有考虑到二叉树底层节点数量远多于顶层节点的性质。
- 作者进行更精确的数学计算之后,时间复杂度为O(n)
逻辑部分
一、堆解法
代码中见注解
class Solution {
public int[] topKFrequent(int[] nums, int k) {
//key为num,value为出现的次数
Map<Integer, Integer> occurrences = new HashMap<Integer, Integer>();
for (int num : nums) {
occurrences.put(num, occurrences.getOrDefault(num, 0) + 1);
}
// int[] 的第一个元素代表数组的值,第二个元素代表了该值出现的次数
//PriorityQueue是优先队列,按照比较器(Comparator)的逻辑来比较元素
//若要实现升序排序,当第一个参数 < 第二个参数时返回负数,相等时返回 0;
//若要实现降序排序,当第一个参数 > 第二个参数时返回负数,相等时返回 0。
//也可以简单理解成 return出的参数和compare中参数相对位置一致是升序,相反是降序
//这里是 第一种情况升序
PriorityQueue<int[]> queue = new PriorityQueue<int[]>(new Comparator<int[]>() {
public int compare(int[] m, int[] n) {
return m[1] - n[1];
}
});
//entrySet()放回map中的每个键值对组成的集合
for (Map.Entry<Integer, Integer> entry : occurrences.entrySet()) {
int num = entry.getKey(), count = entry.getValue();
//如果queue大小已经等于k,判断队列第一个元素的[1]也就是最小出现频率是否大于当前count
if (queue.size() == k) {
//当前count > peek()[1],弹出队首元素,将当前数字及频率创建数组添加到queue中
if (queue.peek()[1] < count) {
queue.poll();
queue.offer(new int[]{num, count});
}
} else {
queue.offer(new int[]{num, count});
}
}
//创建大小为k的数组,保存最后结果
int[] ret = new int[k];
for (int i = 0; i < k; ++i) {
ret[i] = queue.poll()[0];
}
return ret;
}
}
索引排序
- 适用于map和value都是Integer类型
- 在1的前提下巧妙之处是将map的key和value调换
- 那么索引在
public List<Integer> topKFrequent(int[] nums, int k) {
List<Integer>[] bucket = new List[nums.length + 1];
Map<Integer, Integer> frequencyMap = new HashMap<Integer, Integer>();
for (int n : nums) {
frequencyMap.put(n, frequencyMap.getOrDefault(n, 0) + 1);
}
for (int key : frequencyMap.keySet()) {
int frequency = frequencyMap.get(key);
if (bucket[frequency] == null) {
bucket[frequency] = new ArrayList<>();
}
bucket[frequency].add(key);
}
List<Integer> res = new ArrayList<>();
//出现频次高的在列表后面,使用倒序遍历,
//停止条件为 pos >= 0,有可能数组里面数字的种类凑不齐k个数
//res.size() < k表示res已经记录了出现频次最高的k个数字
for (int pos = bucket.length - 1; pos >= 0 && res.size() < k; pos--) { //不为空的添加到列表中
if (bucket[pos] != null) {
res.addAll(bucket[pos]);
}
}
return res;
}
相似习题
692. 前K个高频单词 - 力扣(LeetCode)
451. 根据字符出现频率排序 - 力扣(LeetCode)
(bucket[pos]);
}
}
return res;
}
#### 相似习题
[692. 前K个高频单词 - 力扣(LeetCode)](https://leetcode.cn/problems/top-k-frequent-words/description/)
[451. 根据字符出现频率排序 - 力扣(LeetCode)](https://leetcode.cn/problems/sort-characters-by-frequency/)
显然这两道题,区别在于存储出现频率时,key为String/Character,value为Integer,其他的逻辑部分大差不差,具体实现不同需要自己补充了解