一、训练开发测试集

在配置训练、验证和测试数据集的过程中做出正确决策会在很大程度上帮助创建高效的神经网络。训练神经网络时，需要做出很多决策，例如：

• 神经网络分多少层
• 每层含有多少个隐藏单元
• 学习速率是多少
• 各层采用哪些激活函数

通常将样本分成训练集，验证集和测试集三部分，数据集规模相对较小，适用传统的划分比例，数据集规模较大的，验证集和测试集要小于数据总量的20%或10%。后面我会给出如何划分验证集和测试集的具体方法。

• 没有测试集也不要紧，测试集的目的是对最终所选定的神经网络系统做出无偏估计，如果不需要无偏估计，也可以不设置测试集。

• 所以如果只有验证集，没有测试集，我们要做的就是，在训练集上训练，尝试不同的模型框架，在验证集上评估这些模型，然后迭代并选出适用的模型。因为验证集中已经涵盖测试集数据，其不再提供无偏性能评估。
  

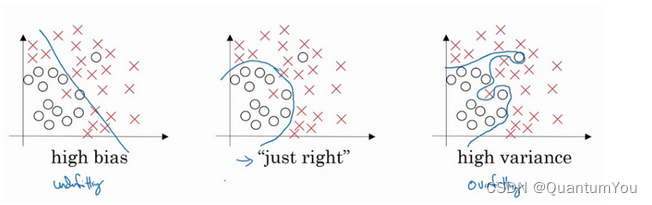
关键看蓝色曲线

• 假设这就是数据集，如果给这个数据集拟合一条直线，可能得到一个逻辑回归拟合，但它并不能很好地拟合该数据，这是高偏差（high bias）的情况，我们称为“欠拟合”（underfitting）。

• 相反的如果我们拟合一个非常复杂的分类器，比如深度神经网络或含有隐藏单元的神经网络，可能就非常适用于这个数据集，但是这看起来也不是一种很好的拟合方式分类器方差较高（high variance），数据过度拟合（overfitting）。

• 线性高偏差，过度拟合高方差

理解偏差和方差的两个关键数据是训练集误差（Train set error）和验证集误差（Dev set error）

二、机器学习基础

在机器学习中，偏差（Bias）和方差（Variance）是用来衡量模型预测性能的两个关键指标。

• 偏差：它描述的是模型预测值与真实值之间的差异程度，即模型的预测准确度。一个高偏差的模型意味着它的预测结果通常会偏离真实值，这通常是因为模型本身的拟合能力不足。
• 方差：它则描述的是模型对于训练数据集中的微小变动所做出的预测结果的变化程度，即模型的稳定性。一个高方差的模型对数据中的噪声非常敏感，导致在不同训练集上训练得到的模型性能波动很大。

偏差：训练集 方差：验证集

高偏差说明模型泛化能力差，换个数据集就不行了

这是我在训练神经网络时用到地基本方法，初始模型训练完成后，首先要知道算法的偏差高不高，如果偏差较高，试着评估训练集或训练数据的性能。如果偏差的确很高，甚至无法拟合训练集，那么要做的就是选择一个新的网络，比如含有更多隐藏层或者隐藏单元的网络，或者花费更多时间来训练网络，或者尝试更先进的优化算法。

三、 正则化初步介绍

• 深度学习可能存在过拟合问题——高方差，有两个解决方法，一个是正则化，另一个是准备更多的数据
  

• 在Python编程语言中， λ 是一个保留字段，编写代码时，我们删掉 α ，写成 lambd ，以免与Python中的保留字段冲突.
  L1和L2正则化是机器学习中用于避免过拟合的技术，它们通过在损失函数中加入一个正则项来实现。

L1正则化，也称为Lasso回归，通过在损失函数中加入权重参数的绝对值之和来限制模型复杂度。这通常会导致一些权重参数变为零，从而实现特征选择的效果。其公式可以表示为：
$$L=E_{in}+\lambda \sum _j|w_j|$$
其中，$E_{in}$ 是未包含正则化项的训练样本误差，$\lambda$ 是正则化参数。

L2正则化，也称为岭回归，它在损失函数中加入权重参数的平方和。这种方式使得权重参数接近于零但不完全为零，得到的解比较平滑。其公式可以表示为：
$$L=E_{in}+\lambda \sum _j{w}_j^2$$
同样，$E_{in}$ 是未包含正则化项的训练样本误差，$lambda$ 是正则化参数。

这两种正则化方法的选择取决于具体问题和数据特性。L1正则化适用于特征选择，当某些特征对模型几乎没有贡献时，L1正则化可以将对应的权重参数压缩为零。而L2正则化适用于当所有特征都对模型有所贡献，但它又希望建立一种相对平稳的权重分布时。

感觉有点迷糊

正则化就是让参数的梯度更快的下降，只不过更快的程度取决于参数本身，区别于一个固定的使梯度下降更快的值

为什么正则化有利于预防过拟合？

• 弗罗贝尼乌斯范数是矩阵范数的一种，用于衡量矩阵大小或长度的度量。

具体来说，弗罗贝尼乌斯范数（Frobenius Norm）通常定义为矩阵中所有元素的平方和的平方根。如果有一个 m×n 的矩阵 A，其元素为 a_ij，则 A 的弗罗贝尼乌斯范数可以表示为：

$$\Vert A{\Vert }_F=\sqrt{\sum _{i=1}^m\sum _{j=1}^n|a_{ij}{|}^2}$$

此外，对于复数矩阵，弗罗贝尼乌斯范数还考虑了共轭转置，即矩阵 A 与其共轭转置 A* 的元素乘积之和的平方根。这个定义在数学上更为严格，尤其是在涉及到复数域时。

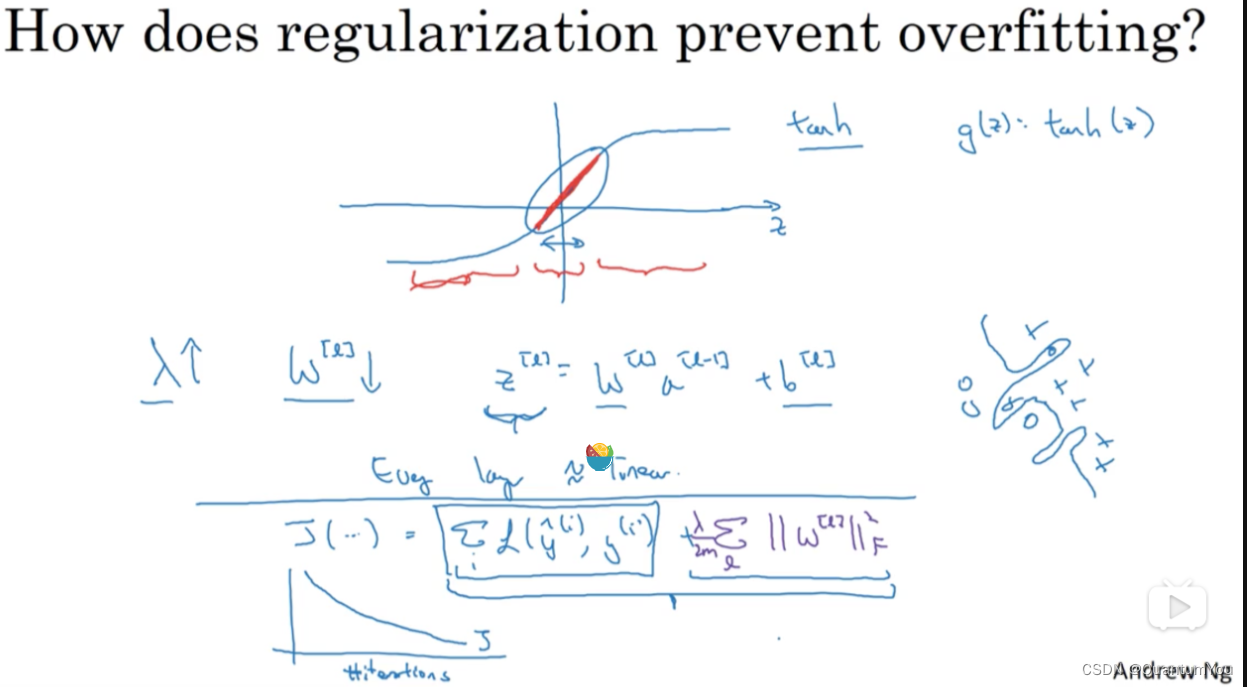
• 直观上理解就是如果正则化 λ 设置得足够大，权重矩阵 w 被设置为接近于0的值，直观理解就是把多隐藏单元的权重设为0，于是基本上消除了这些隐藏单元的许多影响。如果是这种情况，这个被大大简化了的神经网络会变成一个很小的网络，小到如同一个逻辑回归单元，可是深度却很大，它会使这个网络从过度拟合的状态更接近左图的高偏差状态。但是 λ 会存在一个中间值，于是会有一个接近“Just Right”的中间状态。

假设我们使用双曲线激活函数，并考虑L2正则化（这是最常见的正则化形式之一），正则化项通常是这样的形式：λ * ∑|w_i|^2，其中λ是正则化系数，w_i是模型的权重参数。当λ增大时，正则化项在损失函数中的权重也增大，从而促使优化算法在寻找最小损失时，更倾向于选择权重较小的模型。

λ增大 w 减小

• tanh 图像，用 g(z) 表示 tanh(z) ,那么我们发现，只要 z 非常小，如果 z 只涉及少量参数，这里我们利用了双曲正切函数的线性状态，只要 z 可以扩展为这样的更大值或者更小值，激活函数开始变得非线性。
  
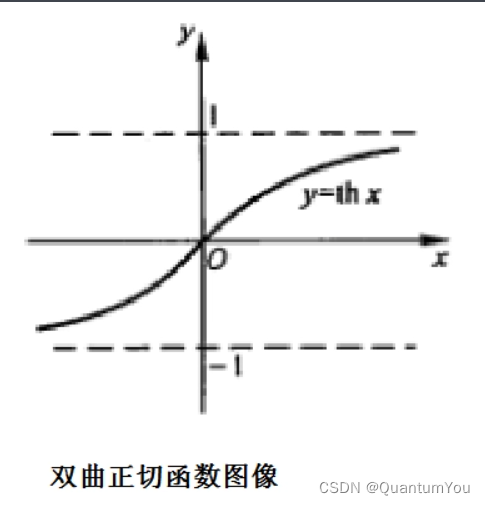
• 如果正则化参数 λ 很大，激活函数的参数会相对较小，因为代价函数中的参数变大了，如果 w 很小，

z=wa+b ,总结一下，如果正则化参数变得很大，参数 w 很小，z 也会相对变小，此时忽略 b 的影响，z 会相对变小，实际上，z 的取值范围很小，这个激活函数，也就是曲线函数 tanh 会相对呈线性，整个神经网络会计算离线性函数近的值，这个线性函数非常简单，并不是一个极复杂的高度非线性函数，不会发生过拟合。

• 这里d3是一个矩阵，表示第三层输出中，由一堆0和1组成，这表示将输出矩阵的某些部位设为0，也就是抹除掉，也就达到了前面dropout的目的，这里的对比是通过这个元素乘法实现的

四、Dropout 正则化

除了 L2 正则化，还有一个非常实用的正则化方法——“Dropout（随机失活）

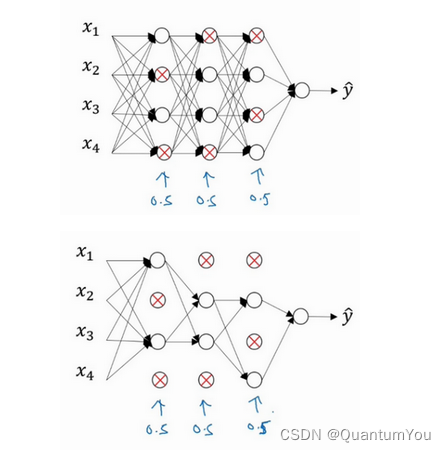
• 假设你在训练上图这样的神经网络，它存在过拟合，这就是dropout所要处理的，我们复制这个神经网络，dropout会遍历网络的每一层，并设置消除神经网络中节点的概率。假设网络中的每一层，每个节点都以抛硬币的方式设置概率，每个节点得以保留和消除的概率都是0.5，设置完节点概率，我们会消除一些节点，然后删除掉从该节点进出的连线，最后得到一个节点更少，规模更小的网络，然后用backprop方法进行训练。
• 这是网络节点精简后的一个样本，对于其它样本，我们照旧以抛硬币的方式设置概率，保留一类节点集合，删除其它类型的节点集合。对于每个训练样本，我们都将采用一个精简后神经网络来训练它，这种方法似乎有点怪，单纯遍历节点，编码也是随机的，可它真的有效。不过可想而知，我们针对每个训练样本训练规模极小的网络，最后你可能会认识到为什么要正则化网络，因为我们在训练极小的网络。

Dropout是一种正则化技术，在深度学习中被广泛用于防止神经网络过拟合。它的工作原理是遍历神经网络的每一层，并为每一层的节点设置一个保留概率（keep_prob），即这些节点在训练过程中被保留的概率。通常，这个概率值介于0和1之间。例如，如果keep_prob设置为0.5，那么在每次训练迭代中，每一层的每个节点都有50%的概率被随机“丢弃”或失活。

Dropout的主要目的是使神经网络不会过于依赖任何一个特定的节点，从而防止模型过拟合。通过随机地“关闭”一部分节点，模型被迫学习更为鲁棒的特征表示，因为它不能总是依赖同一组节点来做出预测。这有点类似于L2正则化，都是通过限制模型的复杂度来减轻过拟合。

然而，在测试阶段，我们通常不使用dropout，因为我们希望模型的输出是稳定的，而不是随机的。因此，为了补偿训练阶段由于dropout造成的权重缩放，我们引入了“反向随机失活”（Inverted Dropout）的概念。

在Inverted Dropout中，每个节点的输出不是直接乘以keep_prob，而是在丢弃节点之后，将剩余的节点输出除以keep_prob。这样做的目的是确保在训练阶段，即使一部分节点被丢弃，神经网络的每一层的输出期望值（均值）仍然保持不变。这样，在测试阶段关闭dropout时，模型的输出可以与训练阶段保持一致，无需进行额外的调整。

例如，假设第三层有50个神经元，在某一次迭代中，平均有10个神经元被dropout归零。如果我们不调整剩余神经元的输出，那么第三层的输出将减少20%。为了弥补这一差距，我们需要将剩余神经元的输出除以0.8（即1-0.2），以确保第三层的输出期望值与没有dropout时相同。

总之，Inverted Dropout是一种技巧，它允许我们在训练时使用dropout来防止过拟合，同时在测试时保持模型的输出稳定，无需进行额外的调整。

dropout一大缺点就是代价函数 J 不再被明确定义，每次迭代，都会随机移除一些节点，如果再三检查梯度下降的性能，实际上是很难进行复查的。定义明确的代价函数 J 每次迭代后都会下降，因为我们所优化的代价函数 J 实际上并没有明确定义，或者说在某种程度上很难计算，所以我们失去了调试工具来绘制这样的图片。我通常会关闭dropout函数，将keep-prob的值设为1，运行代码，确保J函数单调递减。然后打开dropout函数，希望在dropout过程中，代码并未引入bug。我觉得你也可以尝试其它方法，虽然我们并没有关于这些方法性能的数据统计，但你可以把它们与dropout方法一起使用

五、其他正则化方法

数据增强

图像裁剪、图像镜像

early stopping
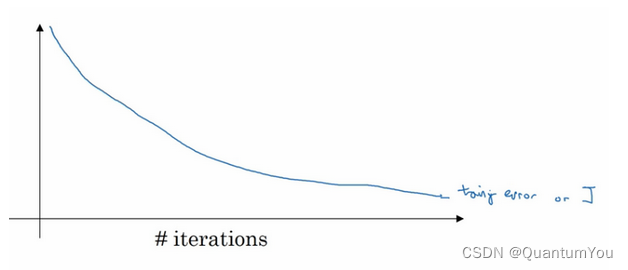
运行梯度下降时，我们可以绘制训练误差，或只绘制代价函数的优化过程，在训练集上用0-1记录分类误差次数。呈单调下降趋势，如图。

• 因为在训练过程中，我们希望训练误差，代价函数 J JJ 都在下降，通过early stopping，我们不但可以绘制上面这些内容，还可以绘制验证集误差，它可以是验证集上的分类误差，或验证集上的代价函数，逻辑损失和对数损失等，你会发现，验证集误差通常会先呈下降趋势，然后在某个节点处开始上升，early stopping的作用是，你会说，神经网络已经在这个迭代过程中表现得很好了，我们在此停止训练吧，得到验证集误差，它是怎么发挥作用的？

• 当你还未在神经网络上运行太多迭代过程的时候，参数 w 接近0，因为随机初始化 w 值时，它的值可能都是较小的随机值，所以在你长期训练神经网络之前 w 依然很小，在迭代过程和训练过程中 w 的值会变得越来越大，比如在这儿，神经网络中参数 w 的值已经非常大了，所以early stopping要做就是在中间点停止迭代过程，我们得到一个 w 值中等大小的弗罗贝尼乌斯范数，与 L2 正则化相似，选择参数 w 范数较小的神经网络，但愿你的神经网络过度拟合不严重

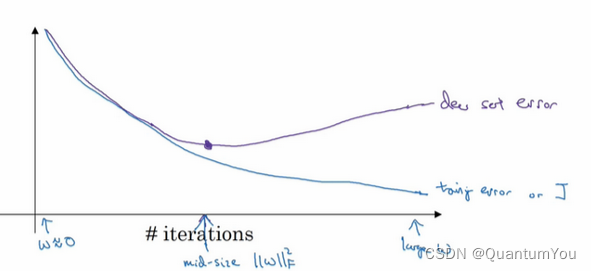
• 缺点：就是不能独立地处理这两个问题，因为提早停止梯度下降，也就是停止了优化代价函数 J ，因为现在你不再尝试降低代价函数 J ，所以代价函数 J 的值可能不够小，同时又希望不出现过拟合，你没有采取不同的方式来解决这两个问题，而是用一种方法同时解决两个问题，这样做的结果是我要考虑的东西变得更复杂。

如果不用early stopping，另一种方法就是 L2 正则化，训练神经网络的时间就可能很长。我发现，这导致超级参数搜索空间更容易分解，也更容易搜索，但是缺点在于，你必须尝试很多正则化参数 λ 的值，这也导致搜索大量 λ 值的计算代价太高。

• 优点：只运行一次梯度下降，你可以找出 w 的较小值，中间值和较大值，而无需尝试 L2 正则化超级参数 λ 的很多值。

六、归一化输入介绍

深度学习归一化是一种数据预处理技术，主要用于将输入数据转换为一定的分布，以便更好地适应深度学习模型的训练。在深度学习中，归一化主要解决输入数据的量纲差异问题，避免输入数据分布过于偏斜或稀疏，从而提高模型的训练效果。

归一化的具体作用可以归纳为：

1. 归纳统一样本的统计分布性，使得数据更容易被模型学习。
2. 统一数据到特定的分布范围，如[0,1]或[-1,1]，或者转换为均值为0、标准差为1的分布（即z-score归一化）。
3. 加快模型训练时的收敛速度，使模型训练过程更加稳定，避免梯度爆炸或梯度消失。

常见的归一化方法包括：

1. Min-Max归一化：将数据缩放到特定的范围内，如[0,1]或[-1,1]。
2. 标准化（Standardization）：通常指将数据转换为均值为0、标准差为1的分布，也称为z-score归一化。
3. Batch Normalization（BN）：2015年提出的数据归一化方法，通常用在深度神经网络中激活层之前。它的作用可以加快模型训练时的收敛速度，使模型训练过程更加稳定，避免梯度爆炸或梯度消失，同时起到一定的正则化作用。

在深度学习中，代价函数（Cost Function）或损失函数（Loss Function）$J(w,b)$用于衡量模型预测值与实际值之间的差异，其中$w$和$b$分别代表模型的权重和偏置项。代价函数的具体形式取决于问题的类型和模型的结构。

对于回归问题，常见的代价函数是均方误差（Mean Squared Error, MSE），其公式为：

为什么我们想要归一化输入特征，回想一下 代价函数
$$J(w,b)=\frac{1}{2m}\sum _{i=1}^m(h_{w,b}(x^{(i)})-y^{(i)}{)}^2$$

其中：

• $m$ 是训练样本的数量。
• $x^{(i)}$ 是第 $i$ 个训练样本的特征。
• $y^{(i)}$ 是第 $i$ 个训练样本的实际标签。
• $h_{w,b}(x^{(i)})$ 是模型使用权重 $w$ 和偏置 $b$ 对第 $i$ 个样本的预测值。

对于分类问题，特别是当使用逻辑回归或神经网络进行二分类时，常用的代价函数是交叉熵损失（Cross-Entropy Loss）：

$$J(w,b)=-\frac{1}{m}\sum _{i=1}^m[y^{(i)}\log (a^{(i)})+(1-y^{(i)})\log (1-a^{(i)})]$$

其中：

• $a^{(i)}$ 是模型对第 $i$ 个样本的预测概率（通常是经过sigmoid函数后的输出）。
• $y^{(i)}$ 是第 $i$ 个样本的实际标签，通常表示为0或1。

对于多分类问题，通常使用softmax函数和相应的交叉熵损失。

此外，根据问题的特性和模型的复杂性，还可能有其他形式的代价函数，如Hinge损失（用于支持向量机）、Huber损失（结合了MSE和MAE的特性）等。

在选择代价函数时，需要考虑问题的性质、数据的分布以及模型的复杂性。同时，代价函数通常与优化算法（如梯度下降、Adam等）一起使用，以在训练过程中调整模型的参数$w$和$b$，从而最小化预测误差。

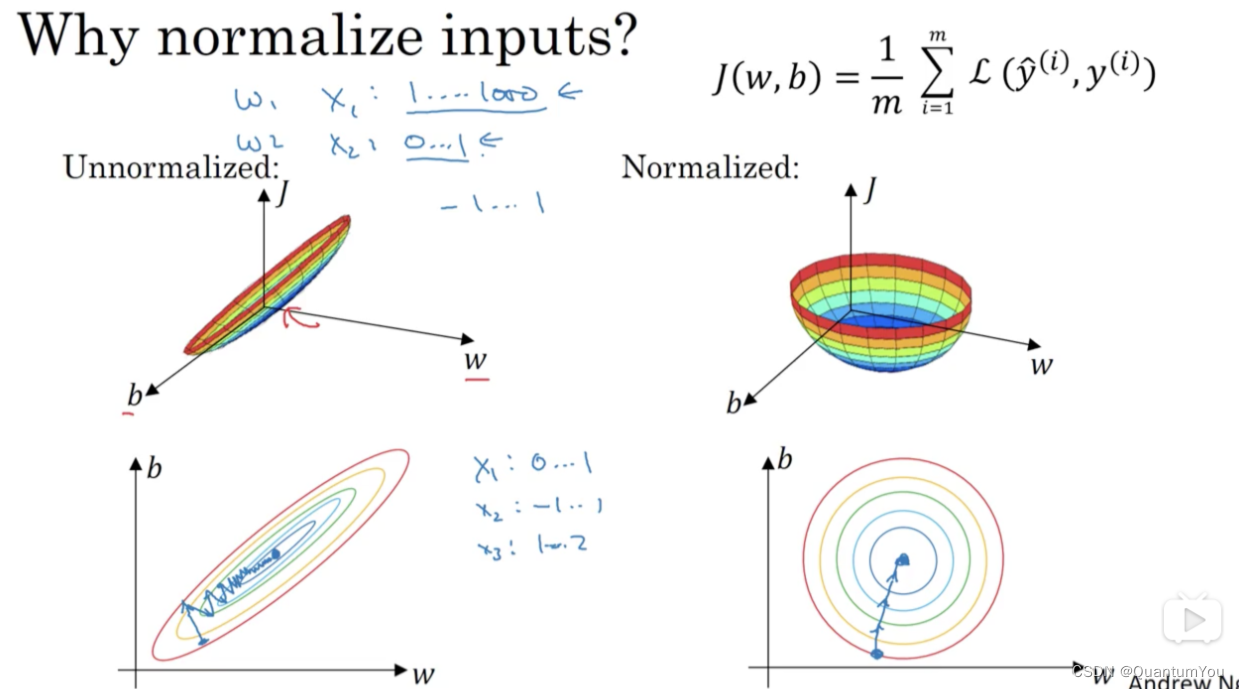
当它们在非常不同的取值范围内，如其中一个从1到1000，另一个从0到1，这对优化算法非常不利。但是仅将它们设置为均化零值，假设方差为1，就像上一张幻灯片里设定的那样，确保所有特征都在相似范围内，通常可以帮助学习算法运行得更快。

所以如果输入特征处于不同范围内，可能有些特征值从0到1，有些从1到1000，那么归一化特征值就非常重要了。如果特征值处于相似范围内，那么归一化就不是很重要了。执行这类归一化并不会产生什么危害，我通常会做归一化处理，虽然我不确定它能否提高训练或算法速度。

这就是归一化特征输入，下节课我们将继续讨论提升神经网络训练速度的方法。

七、梯度消失与梯度爆炸

• 训练神经网络，尤其是深度神经所面临的一个问题就是梯度消失或梯度爆炸，也就是训练神经网络的时候，导数或坡度有时会变得非常大，或者非常小，甚至于以指数方式变小，这加大了训练的难度。

梯度消失和梯度爆炸是深度学习中训练深度神经网络时常遇到的两个问题。它们都与网络的深度和反向传播算法有关。

梯度消失问题：

1. 原因：在深度网络中，由于链式法则导致的连乘效应，梯度在每一层传播时会不断乘以权重矩阵。如果这些权重矩阵的元素值较小，梯度就会迅速减小，导致网络较深层次的参数更新变得非常缓慢。
2. 影响：梯度消失使得网络难以学习到长距离的依赖关系，因为梯度值太小，网络无法有效更新权重和偏置项。
3. 解决方法：使用ReLU（Rectified Linear Unit）激活函数、批量归一化（Batch Normalization）、残差网络（Residual Networks）等技术可以缓解梯度消失的问题。

梯度爆炸问题：

1. 原因：与梯度消失相反，梯度爆炸是因为连乘效应中的梯度值过大，导致在传播过程中梯度迅速增大。
2. 影响：梯度爆炸会导致网络参数的更新变得过大，从而使得网络训练不稳定，甚至导致模型完全失效。
3. 解决方法：梯度裁剪（Gradient Clipping）、使用合适的初始化方法、短程记忆网络（如LSTM）等技术可以帮助控制梯度的大小，防止梯度爆炸。

总的来说，为了避免这两个问题，研究人员通常会采用多种策略，包括使用更先进的优化器（如Adam、RMSprop等），以及设计更合理的网络架构。此外，适当的预训练和微调（Pre-training and Fine-tuning）也是解决这些问题的有效方法之一。在实际应用中，通常需要结合具体的任务和数据集来选择合适的策略，以确保网络能够有效地学习和泛化。

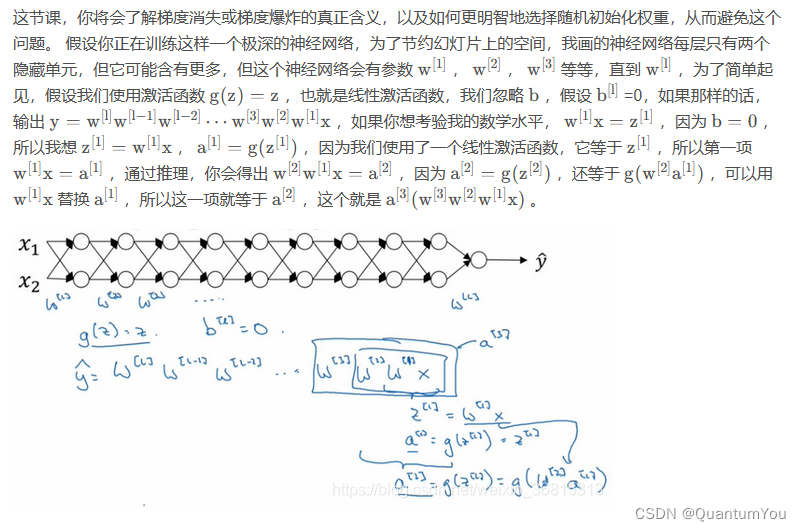
八、神经网络的权重初始化

Xavier初始化

Xavier初始化方法的目标是使每一层的输出方差保持一致，尽量避免梯度消失或梯度爆炸的问题。该方法的核心思想是，根据每一层的输入和输出的维度来选择合适的参数初始化范围。

假设某一层的输入维度为n，输出维度为m，Xavier初始化方法会将参数初始化在一个均匀分布的范围内，该范围的上下界分别为±√(6/(n+m))。用LaTex公式表示即为：

$$w\sim U\left[-\frac{\sqrt{6}}{\sqrt{n+m}},\frac{\sqrt{6}}{\sqrt{n+m}}\right]$$

其中，w表示权重，U表示均匀分布。

公式推理：

Xavier初始化方法背后的数学推理主要基于方差的一致性。假设输入和输出的方差均为1，通过选择合适的初始化范围，可以使得权重矩阵与输入数据相乘后的方差仍然接近1，从而保持方差的一致性。这有助于避免梯度消失或梯度爆炸问题，提高神经网络的训练效果。

He初始化

He初始化是何凯明等提出的一种针对ReLU及其变种激活函数的权重初始化方法。ReLU函数在输入为正时输出等于输入，输入为负时输出为0，这种非线性特性使得其与前述的线性激活函数在权重初始化上有所不同。

He初始化方法的主要思想是将权重初始化为一个均值为0，标准差为√(2/n)的高斯分布，其中n为该层的输入神经元数量。用LaTex公式表示即为：

$$w\sim N\left(0,\sqrt{\frac{2}{n}}\right)$$

其中，w表示权重，N表示高斯分布。

公式推理：

ReLU激活函数的特性使得其输出有一半的概率为0。因此，在初始化权重时，需要考虑到这一点。He初始化方法通过设定特定的标准差，使得权重分布与ReLU激活函数的特性相匹配，从而保持前向传播和反向传播时激活值和梯度的方差稳定性。这有助于避免梯度消失或梯度爆炸问题，提高神经网络的训练速度和稳定性。

九、梯度数值逼近和检验

①梯度数值逼近

• 在实施backprop时，有一个测试叫做梯度检验，它的作用是确保backprop正确实施。因为有时候，你虽然写下了这些方程式，却不能100%确定，执行backprop的所有细节都是正确的。为了逐渐实现梯度检验，我们首先说说如何计算梯度的数值逼近，下节课，我们将讨论如何在backprop中执行梯度检验，以确保backprop正确实施。

• 使用双边误差来判断别人给你的函数 g(θ) ，是否正确实现了函数 f 的偏导
  
  ②梯度检验

梯度检验是一种确保反向传播算法正确性的方法，通过比较数值计算的梯度与解析计算的梯度来进行验证。

首先，梯度检验的目的是确保神经网络模型中的梯度计算是正确的，这对于模型的训练至关重要。在深度学习中，由于网络结构复杂，手动检查每一层的梯度是不现实的，因此梯度检验成为了一种有效的自动化工具。它通过比较两种不同方法计算得到的梯度来工作：

• 解析法（Analytical Gradient）：这是通过应用链式法则直接计算梯度的方法。这种方法通常更快，因为它使用了数学公式直接求解，但缺点是容易出错，尤其是在复杂的网络结构中。
• 数值法（Numerical Gradient）：这种方法使用导数的定义，即通过评估函数在非常小的步长变化下的输出变化来近似梯度。数值法通常被认为更准确，但计算成本较高。

在进行梯度检验时，通常会采用以下步骤：

1. 使用解析法计算梯度。
2. 使用数值法计算梯度，通常选择较小的步长以提高准确性。
3. 比较两种方法得到的梯度，计算它们之间的相对误差。如果相对误差在可接受的范围内，那么可以认为梯度计算是正确的。

此外，梯度检验可以帮助识别和修复神经网络实现中的错误，例如错误的权重更新、激活函数的不正确实现或自定义层的问题。它是一种重要的调试工具，有助于提高模型训练的稳定性和可靠性。

在进行梯度检验时，确实有一些重要的注意事项需要遵守：

1. 使用中心差分公式：在数值法中，使用中心差分公式（centered formula）来计算梯度通常比前向或后向差分更精确。这是因为中心差分公式能够更好地近似函数的导数，尤其是在梯度变化剧烈的区域。
2. 计算相对误差：在比较解析梯度和数值梯度时，应该计算它们的相对误差而不是绝对误差。相对误差能够提供更准确的误差估计，因为它考虑到了梯度值的大小。
3. 不在训练中使用梯度检验：梯度检验仅用于调试阶段，而不应该在模型的实际训练过程中使用。因为数值梯度的计算非常耗时，会显著减慢训练速度。一旦确保模型的梯度计算正确，就应该关闭梯度检验功能。
4. 检查所有项：如果梯度检验失败，即解析梯度和数值梯度之间存在较大差异，应该逐一检查每一层的梯度计算，找出可能的错误来源。这可能包括错误的权重更新、激活函数实现不当或其他自定义层的问题。
5. 合理选择步长：在使用数值法计算梯度时，选择合适的步长非常重要。步长太小可能导致数值不稳定，而步长太大则可能导致误差过大。通常，选择一个较小的步长可以提高数值梯度的准确性。
6. 双边误差检验：在进行梯度检验时，使用双边误差检验通常比单边误差检验更加合理，因为它可以提供一个更准确的导数近似值。

总的来说，通过遵循这些注意事项，可以有效地利用梯度检验来确保神经网络模型的反向传播算法的正确性，从而提高模型训练的稳定性和可靠性。

十、上述学习总结

第一题 划分训练/开发/测试集

如果你有10,000,000个例子，你会如何划分训练/开发/测试集？

A.33%训练，33%开发，33%测试

B.60%训练，20%开发，20%测试

C.98%训练，1%开发，20%测试

解答：C

• 在如今的大数据时代，我们通常可以获得庞大的数据集，比如1,000,000条数据，这种情况下，没有必要选择20%的数据量作为开发集，另外20%数据量作为测试集。通常我们选择10,000条数据作为开发集、10,000条数据作为测试集就足够了。即划分比例：98/1/1。因为开发集的目的是测试不同算法在其上的性能，选择性能更好的算法，因此开发集数量足够大足以评估不同算法并选择较优算法即可。同样地，测试集的目的是，给出最终的分类器，让你对它的性能有一个非常自信的估计。

第二题 开发和测试集分布

开发和测试集应该：

A.来自同一分布

B.来自不同分布

C.完全相同（一样的(x, y)对）

D.数据数量应该相同

解答：A

第三题 神经网络方差高解决

如果你的神经网络方差很高，下列哪个尝试是可能解决问题的？

A.添加正则项

B.获取更多测试数据

C.增加每个隐藏层的神经元数量

D.用更深的神经网络

E.用更多的训练数据

解答：AE

• 神经网络具有较高的方差，说明模型处于过拟合。可以通过添加正则化和获取更多的训练数据来解决过拟合问题。

• 过拟合是机器学习中的一个常见问题，它通常发生在模型过于复杂或训练数据不足时。解决过拟合问题可以从多个方面入手，以下是一些常用的方法：

1. 增加训练数据：更多的训练数据可以使模型更好地学习到数据的内在规律，降低过拟合的风险。如果没有更多的真实数据，可以考虑使用数据增强技术来生成新的训练样本。
2. 简化模型结构：选择更简单的模型或降低模型的复杂度可以减少过拟合的可能性。例如，在神经网络中，可以减少神经元的数量或层数。
3. 权重正则化：正则化是一种常用的防止过拟合的技术。通过在损失函数中加入权重的惩罚项（如L1正则化或L2正则化），可以减小权重的大小，从而降低模型的复杂度。
4. Dropout机制：在训练神经网络时，Dropout可以随机将一部分神经元置为零，使得每次训练时模型的结构都有所不同。这有助于防止模型对训练数据的过度拟合。
5. 早停法：在验证误差开始上升时停止训练，可以防止模型在训练数据上过拟合。
6. 集成学习：如Bagging和Boosting等方法，通过结合多个模型的预测结果来提高模型的泛化能力。

第四题 改善分类器效果

你正在为苹果，香蕉和橘子制作分类器。 假设您的分类器在训练集上有0.5％的错误，以及开发集上有7％的错误。 以下哪项尝试是有希望改善你的分类器的分类效果的？

A.增大正则化参数 λ

B.减小正则化参数 λ

C.获取更多训练数据

D.用更大的神经网络

解答：AC

• 训练集上0.5%的错误，开发集上7%的错误，我们可以认为模型处于过拟合状态。过拟合可以通过增加正则化参数lambda以及获取更多的训练数据解决。

第五题 权重衰减定义🔥

什么是权重衰减？

解答：正则化技术（例如L2正则化）导致梯度下降在每次迭代时权重收缩。

第六题 增大正则化的超参数 λ

当你增大正则化的超参数 λ 时会发生什么？

A.权重变小（接近0）

B.重量变大（远离0）

C.2倍的 λ 导致2倍的权重

D.每次迭代，梯度下降采取更大的步距（与 λ 成正比）

解答：A

增加正则化超参数lambda就意味着权重矩阵带来的影响变大，因此权重会变得更小。

第七题 测试使用dropout

在测试时候使用dropout：

A.不随机关闭神经元，但保留1/keep_brob因子

B.随机关闭神经元，保留1/keep_brob因子

C.随机关闭神经元，但不保留1/keep_brob因子

D.不随机关闭神经元，也不保留1/keep_brob因子

解答：D

• 不要随机消除节点，也不要在训练中使用的计算中保留1 / keep_prob因子。在测试阶段不要用dropout，因为那样会使得预测结果变得随机。

第八题 参数keep_prob

将参数keep_prob从（比如说）0.5增加到0.6可能会导致以下情况（选出所有正确项）：

A.正则化效应被增强

B.正则化效应被减弱

C.训练集的误差会增加

D.训练集的误差会减小

解答：BD

• keep_prob增加，则保留的神经元数目变多，模型更为复杂，能够更好地拟合训练集的数据。正则化是引入了惩罚，来防止模型复杂的一种手段，因此，keep_prob增加也会导致正则化效应被削弱。

• 将参数 keep_prob 从 0.5 增加到 0.6 可能会导致以下情况：

• 减少模型的正则化效果：keep_prob 通常用于控制神经网络中dropout层的丢弃概率。增加 keep_prob 意味着减少了在训练过程中随机丢弃神经元的比例，从而减轻了dropout带来的正则化效果，可能会提高模型复杂度。

• 可能提高模型的训练速度：由于更多的神经元被保留下来参与前向传播和反向传播，这可能导致每次迭代的计算量略有增加，因此有可能加快模型的训练速度。

• 可能改善模型性能：如果原先的 keep_prob 设置过低，导致模型欠拟合，那么适当增加 keep_prob 的值可能有助于模型捕捉到更复杂的特征，从而提升模型的性能。

• 可能导致过拟合：如果数据集较小或者模型已经处于临界过拟合的状态，增加 keep_prob 可能会使得模型更加倾向于过拟合，因为它允许模型有更多的参数来适应训练数据。

第九题 减少方差（减少过拟合）技术

以下哪些技术可用于减少方差（减少过拟合）？（选出所有正确项）

A.梯度消失

B.数据扩充

C.Dropout

D.梯度检查

E.Xavier初始化

F.L2正则化

G.梯度爆炸

解答：BCF

第十题 输入 x 进行正则化

为什么要对输入 x 进行正则化？

A.让参数初始化更快

B.让代价函数更快地优化

C.更容易做数据可视化

D.是另一种正则化——有助减少方差

1. 防止过拟合：通过引入正则化项，可以减少模型参数的自由度，从而降低模型复杂度，避免模型过度拟合训练数据。
2. 提高泛化能力：正则化有助于提高模型在未知数据上的表现，即提高模型的泛化能力。
3. 稳定模型训练：正则化可以减少模型参数的波动，使得模型训练过程更加稳定。
4. 零均值化：在某些情况下，正则化还包括将输入数据的均值调整到零，这有助于打破模型参数之间的对称性，加速梯度下降算法的收敛速度。
5. 特征尺度统一：正则化还可以通过标准化输入数据，使得不同特征具有相同的尺度，这对于基于梯度的优化算法尤为重要，因为它有助于确保所有参数以相似的速度更新。
6. 减少测试误差：虽然正则化可能会增加训练误差，但它的主要目的是减少测试误差，从而提高模型在新数据上的预测性能。
7. 避免极端参数值：正则化可以防止模型参数取到极端的值，这些值可能会导致模型在某些区域过于敏感或者不稳定。
8. 解决多重共线性问题：在回归分析中，如果输入变量之间存在高度相关性，正则化可以帮助缓解多重共线性问题。
9. 提升模型解释性：通过减少不必要的参数，正则化有助于简化模型，使其更容易解释和理解。

综上所述，正则化是机器学习和深度学习中常用的技术，它通过在损失函数中添加额外的约束项来限制模型的复杂度，从而达到提升模型泛化能力的目的。

十一、 Mini-batch 梯度下降

进一步介绍深度学习优化算法

Mini-batch 梯度下降是一种在批量梯度下降和随机梯度下降之间的优化算法。

Mini-batch 梯度下降的主要特点是在每次迭代时使用一部分而不是全部的训练样本来更新模型参数。这种方法的目的是为了平衡计算效率和收敛速度。以下是关于 Mini-batch 梯度下降的详细解释：

1. 数据集分割：在每个训练周期（epoch）中，训练集被随机分割成指定大小的小批量（mini-batches）。
2. 随机性：为了提高模型的泛化能力，通常会在每个epoch开始时打乱数据，确保模型不会对特定的数据顺序产生依赖。
3. 计算效率：与批量梯度下降相比，Mini-batch 梯度下降不需要在每次迭代时使用整个训练集，这显著减少了计算量，使得训练过程更加高效。
4. 收敛速度：虽然 Mini-batch 梯度下降的收敛速度可能不如随机梯度下降快，但它通常能提供更稳定的收敛过程，因为它使用的是一批数据的聚合梯度信息。
5. 超参数选择：选择合适的批量大小（batch size）是 Mini-batch 梯度下降中的一个关键因素，它会影响到模型的训练效果和速度。
6. 深度学习中的应用：在深度学习中，由于模型参数众多，使用 Mini-batch 梯度下降可以有效地训练复杂的网络结构，同时保持较高的学习效率。

它通过处理分成小批量的数据集 X { t } X^{\{t\}} X{t}和对应的标签集 Y { t } Y^{\{t\}} Y{t} 来更新模型参数。

Mini-batch 梯度下降是一种在批量梯度下降和随机梯度下降之间的优化策略，它通过处理分成小批量的数据集 (X^{{t}}) 和对应的标签集 (Y^{{t}}) 来更新模型参数。

具体来说，以下是关于 Mini-batch 梯度下降的介绍：

1. 数据集划分：在 Mini-batch 梯度下降中，整个训练数据集被划分为多个小批量（mini-batches），每个小批量包含一定数量的样本。例如，如果有 (m) 个样本，每个 batch 的大小为 64，那么可以分成 (m/64) 个 batch，如果 (m) 不能被 64 整除，则最后一个 batch 的大小为 (m\mod 64)。
2. 梯度计算：对于每个 mini-batch，计算代价函数对权重参数的偏导数，即梯度。代价函数 (J) 是所有样本上损失值的和，其中 y { i }   y^{\{i\}}\ y{i} 是真实值，ŷ^{i}是模型的预测值。
3. 参数更新：使用计算出的梯度来更新模型的权重参数 (w)，更新规则为 w = w - \alpha \ast w∂J)，其中 (\alpha) 是学习率。
4. 效率与准确性：Mini-batch 梯度下降旨在平衡训练的效率和准确性。与全批量梯度下降相比，它减少了每次迭代所需的计算量，提高了训练速度；与随机梯度下降相比，它提供了更稳定的收敛过程，因为它使用的是一批数据的聚合梯度信息
   
   mini batch 取中间的情况 ---->绿色字体
   
   

对mini-batch作用的理解：
1）适应gpu/cpu内存大小，因为无法一次性存储所有的参数，所以需要mini-batch；
2）mini-batch的收敛快于batch，因为batch训练一次参数量大，计算量大，且一轮仅更新一次所有参数；mini-batch每一个小batch就更新一次所有参数。如果小batch和batch都独立同分布，那么每次小batch的参数更新都能加速向全局最优收敛。而mini-batch一轮更新了k次参数，因此mini-batch收敛快于batch

十二、指数加权平均

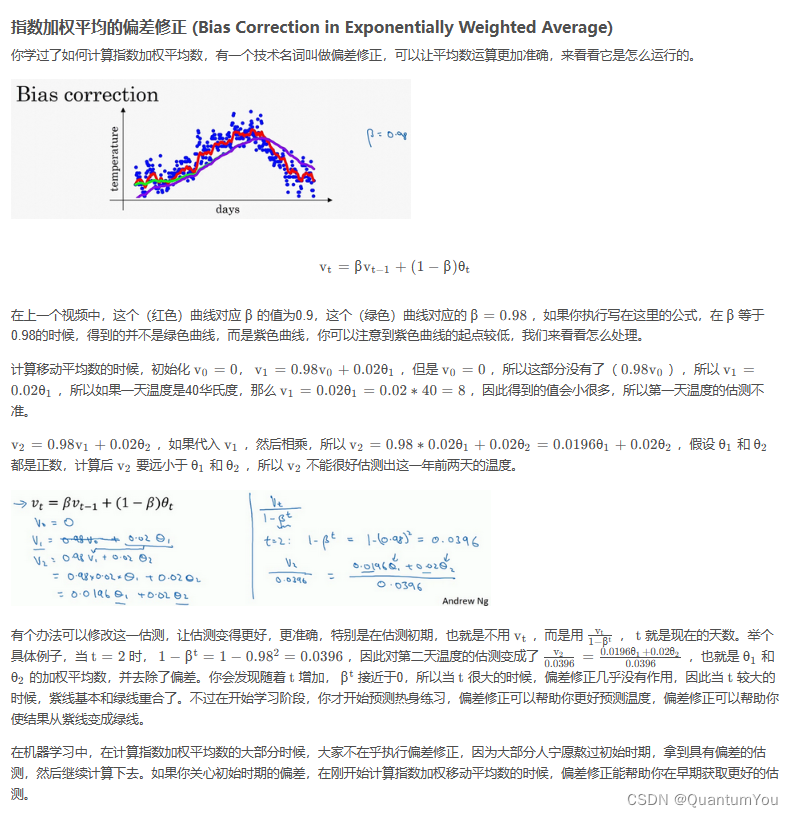
展示几个优化算法，它们比梯度下降法快，要理解这些算法， 需要用到指数加权平均，在统计中也叫做指数加权移动平均

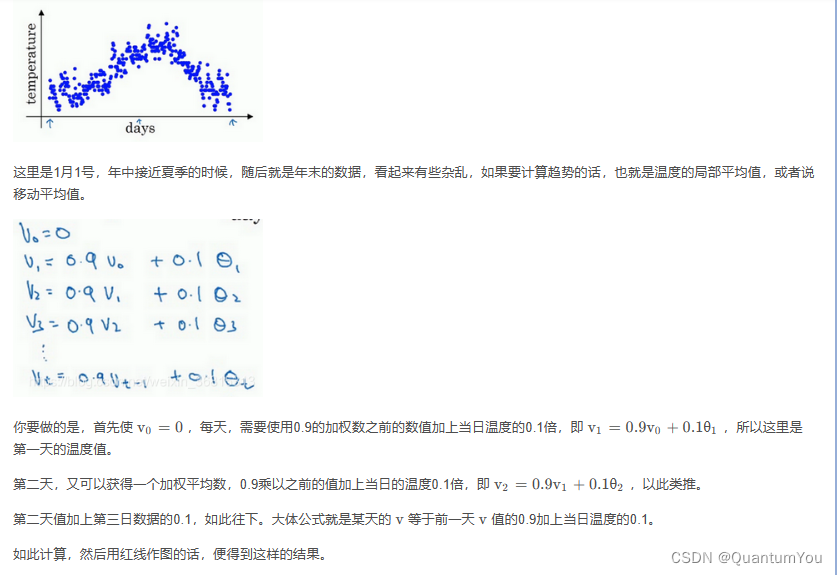
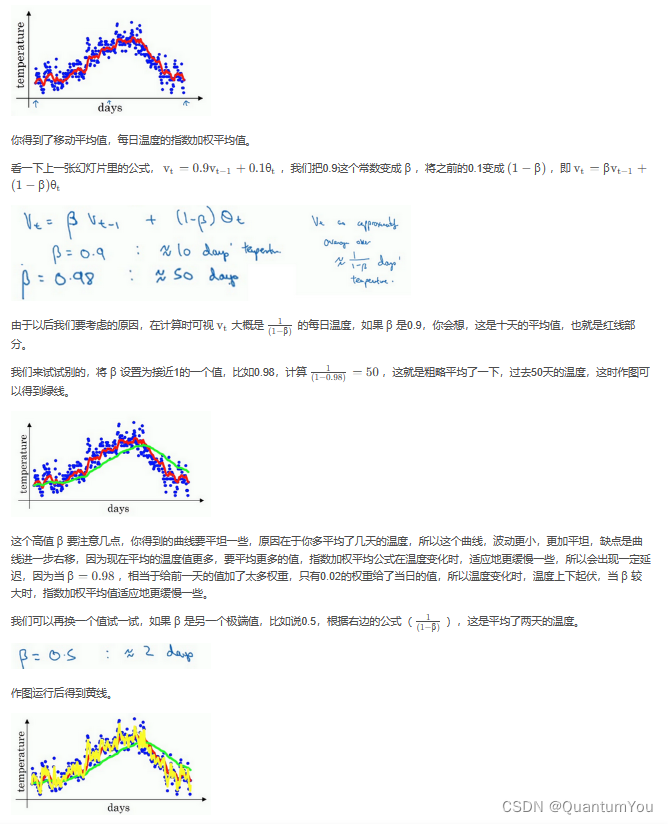
• β=0.9 的时候，得到的结果是红线，如果它更接近于1，比如0.98，结果就是绿线，如果 β 小一点，如果是0.5，结果就是黄线

指数加权平均的深入理解

指数加权平均数的关键方程可以使用LaTeX表示为：

$$v_t=\beta v_{t-1}+(1-\beta ){\theta }_t$$

其中，各个符号的含义如下：

• ( v_t )：第 ( t ) 个时间步的指数加权平均值。
• ( \beta )：一个介于 0 和 1 之间的超参数，控制平均的平滑程度。
• ( v_{t-1} )：前一个时间步的指数加权平均值。
• ( \theta_t )：第 ( t ) 个时间步的实际值（例如损失值或梯度值）。

指数加权平均的偏差修正

十三、动量梯度下降法

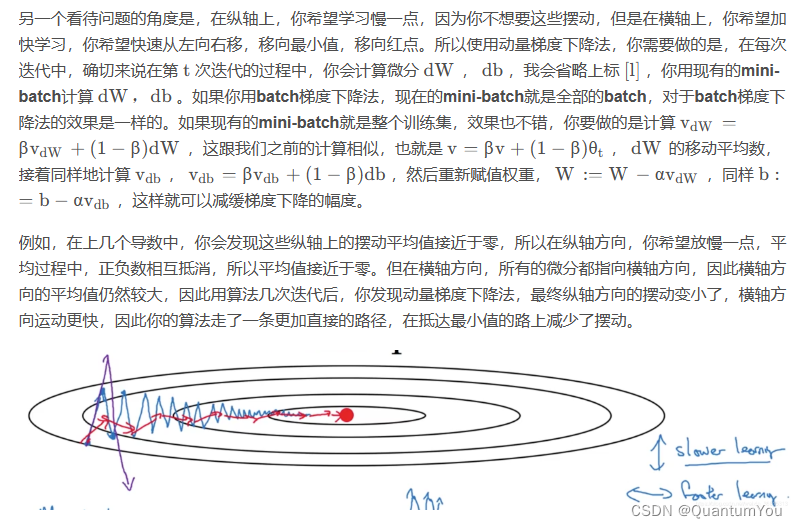
v代表经过指数加权平均后的梯度

• 动量梯度下降法是对梯度下降法的一种改进。传统的梯度下降法在遇到局部最优时可能会停滞不前，而为了解决这一问题，动量梯度下降法引入了动量的概念其基本原理类似于物体从高处滚到低处的运动过程，由于物体具有动量，遇到小坑时会由于原有动量而跃出小坑。因此，动量梯度下降法在迭代的过程中，通过累积之前的梯度信息来加速收敛，并有助于跳出局部最优。

• 动量梯度下降法使用了一个速度变量v来累积梯度信息。在每次迭代中，首先计算当前位置的梯度，然后将梯度与速度变量v进行加权求和，得到新的速度变量。最后，使用新的速度变量来更新模型参数。通过这种方式，动量梯度下降法可以在遇到噪声或局部最优时，利用之前的梯度信息来平滑梯度变化，从而加速收敛并提高算法的稳定性。

此外，动量梯度下降法还有一个重要的超参数：动量衰减率β。它决定了之前梯度信息对当前速度变量的影响程度。一个较大的β值意味着更多的历史梯度信息会被保留，而一个较小的β值则意味着更少的历史梯度信息被考虑。因此，调整β值可以平衡算法的稳定性和收敛速度。

十四、RMSprop 、Adam优化算法

• RMSprop (Root Mean Square Rrop)

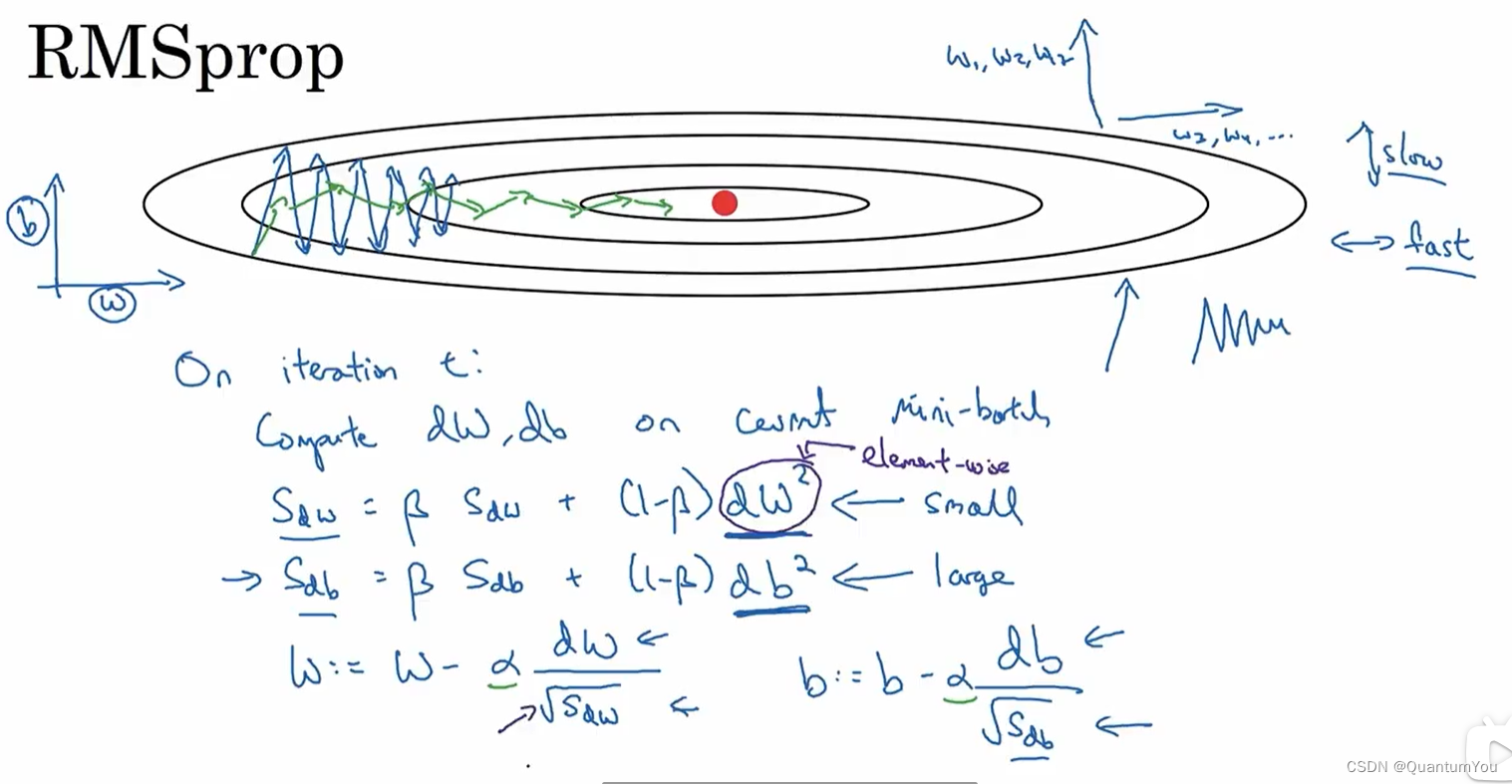
• 回忆一下我们之前的例子，如果你执行梯度下降，虽然横轴方向正在推进，但纵轴方向会有大幅度摆动，为了分析这个例子，假设纵轴代表参数 b ，横轴代表参数 W，可能有 W1，W2或者其它重要的参数，为了便于理解，被称为 b 和 W 。

• 所以，你想减缓 b bb 方向的学习，即纵轴方向，同时加快，至少不是减缓横轴方向的学习，RMSprop算法可以实现这一点。

Adam优化算法 (Adam Optimization Algorithm)

• Adam优化算法基本上就是将Momentum和RMSprop结合在一起

Adam优化算法是一种自适应学习率的梯度下降算法，它结合了Adagrad（Adaptive Gradient Algorithm）和RMSprop（Root Mean Square Propagation）两种优化算法的优点。Adam算法可以自动调整学习率，适用于大规模数据和参数场景，能够很好地处理不稳定目标函数和梯度稀疏或存在很大噪声的问题。

十五、学习率衰减、局部优化问题

• 加快学习算法的一个办法就是随时间慢慢减少学习率，我们将之称为学习率衰减
• epoch是所有数据要训练多少轮，mini-batch是数据划分

深度学习中的局部最优问题通常指的是在优化神经网络模型时，优化算法可能会陷入某个局部最优点，而无法达到全局最优点的情境。这个问题在深度学习领域被广泛讨论，有以下几个重要的观点：

1. 损失函数的特征值分布：当损失函数的值已经非常小的时候，我们可能会遇到局部最小值问题。在这种情况下，损失值已经足够小，我们对当前的解已经比较满意，因此不需要花费更大的力气去寻找全局最优值。
2. 局部最小值与全局最小值的接近性：在一定假设条件下，有研究表明在深度学习中，局部最小值往往很接近于全局最小值。这意味着即使模型收敛到局部最优，其性能也可能与全局最优相差无几。
3. 高维空间的性质：在高维空间中，梯度为零的点通常不是局部最优点的，而是鞍点。在一个具有高维度的空间中，如果梯度为零，那么在不同方向上，函数可能是凸的也可能是凹的。
4. 非凸目标函数的挑战：深度学习模型的目标函数通常是非凸的，这意味着存在多个局部最优解。传统的优化方法如梯度下降只能保证找到局部最优解，而不能保证找到全局最优解。
5. 实际影响：尽管理论上存在局部最优问题，但在实际应用中，通过使用诸如随机初始化、批量归一化、残差连接等技术，以及合理设计的网络结构和优化策略，可以在很大程度上减少局部最优问题的影响。
6. 研究进展：学术界对于深度学习中的局部最优问题持续进行研究，试图更好地理解其性质并提出新的优化算法来缓解这一问题。

十六、编程作业实现

1、作业实现纲要

• 初始化两层的网络和层的神经网络的参数。

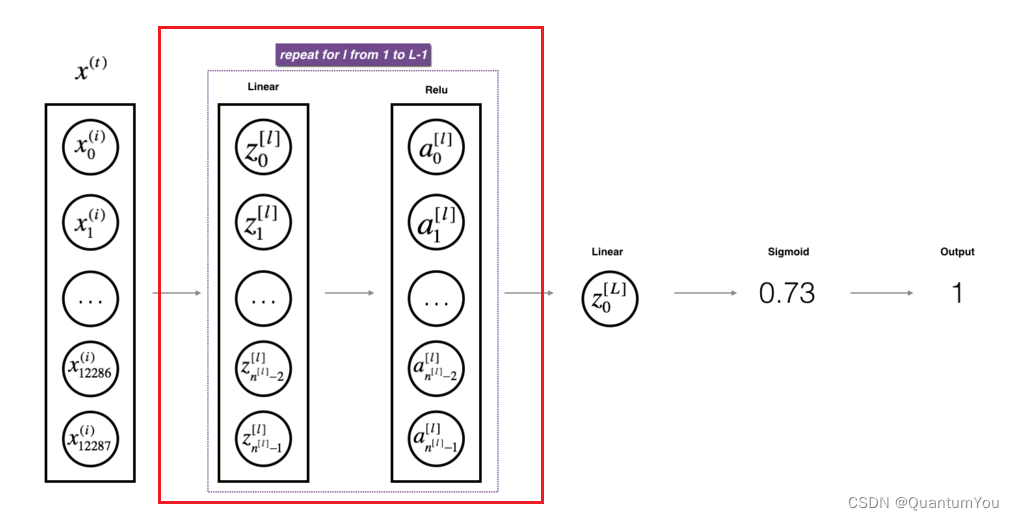
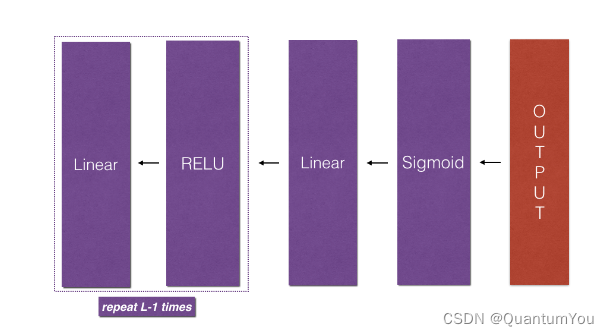
• 实现正向传播模块（在下图中以紫色显示）。

  • 完成模型正向传播步骤的LINEAR部分（Z^[l])
  • 提供使用的ACTIVATION函数（relu / Sigmoid各使用一次）。
  • 将前两个步骤合并为新的[LINEAR-> ACTIVATION]前向函数。
  • 堆叠[LINEAR-> RELU]正向函数L-1次（第1到L-1层），并在末尾添加[LINEAR-> SIGMOID]（最后的层）。这合成了一个新的L_model_forward函数。

• 计算损失。
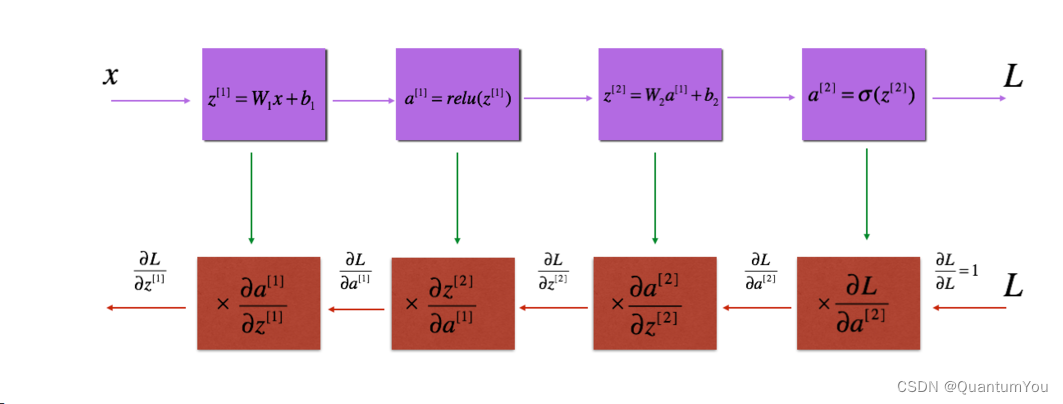
  实现反向传播模块（在下图中以红色表示）。

  • 完成模型反向传播步骤的LINEAR部分。
  • 提供的ACTIVATE函数的梯度（relu_backward / sigmoid_backward）
  • 将前两个步骤组合成新的[LINEAR-> ACTIVATION]反向函数。
  • 将[LINEAR-> RELU]向后堆叠L-1次，并在新的L_model_backward函数中后向添加[LINEAR-> SIGMOID]

• 最后更新参数。
  

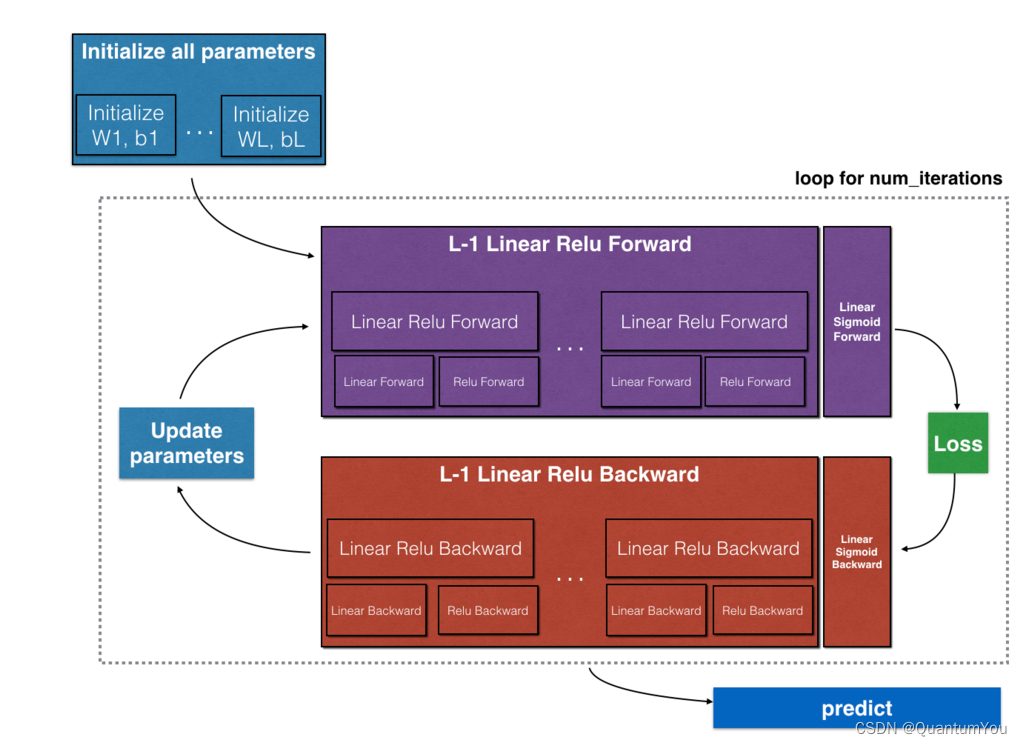
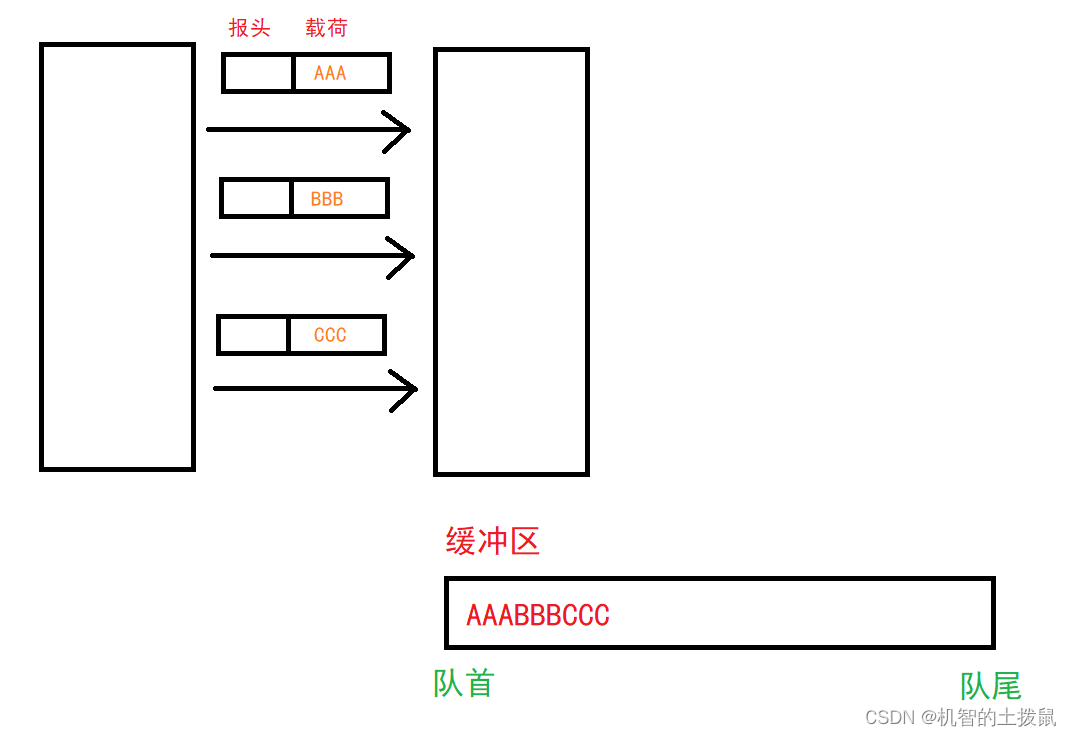
注意：对于每个正向函数，都有一个对应的反向函数。 这也是为什么在正向传播模块的每一步都将一些值存储在缓存中的原因。缓存的值可用于计算梯度。 然后，在反向传导模块中，你将使用缓存的值来计算梯度。 此作业将指导说明如何执行这些步骤。

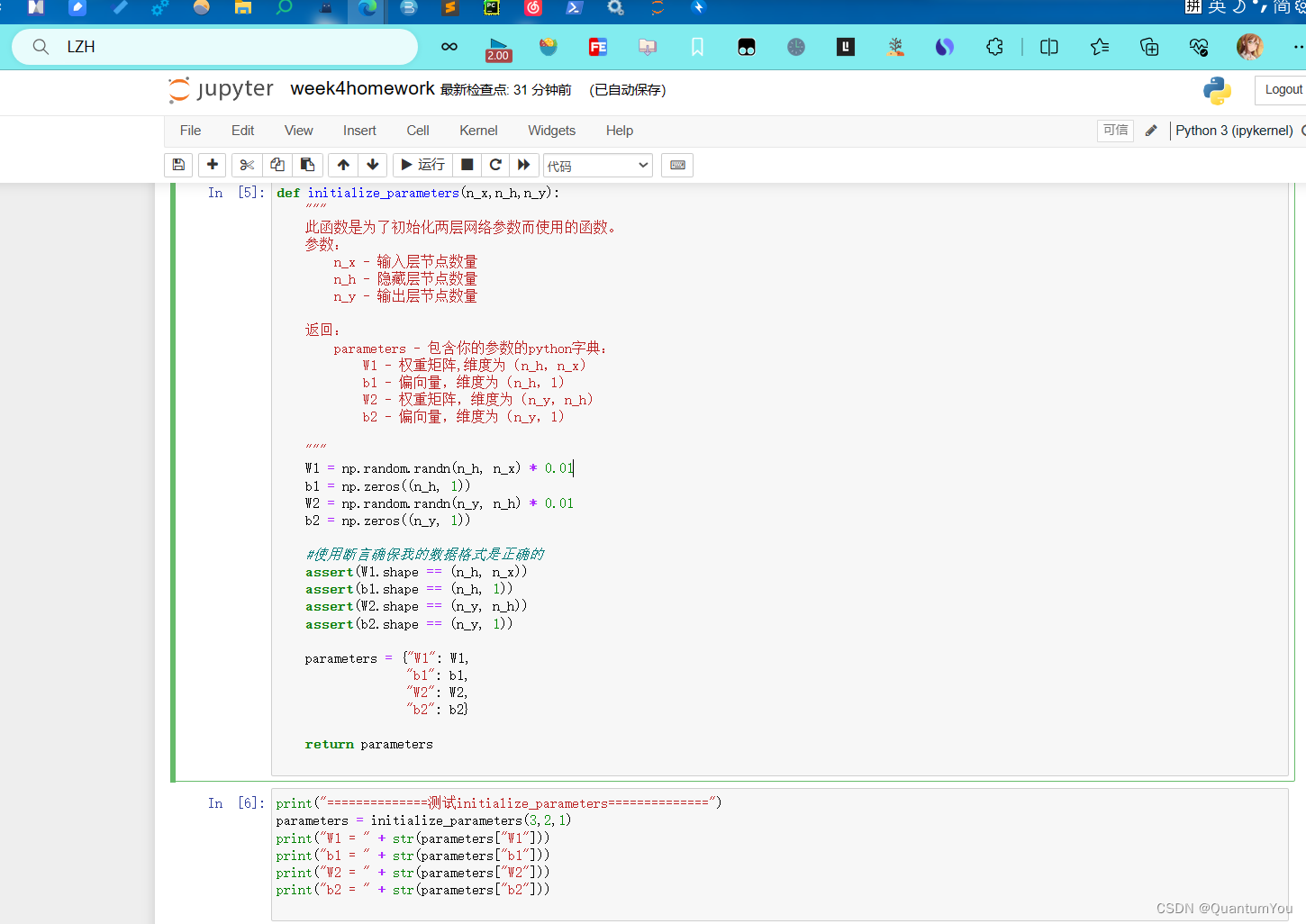
2、初始化参数

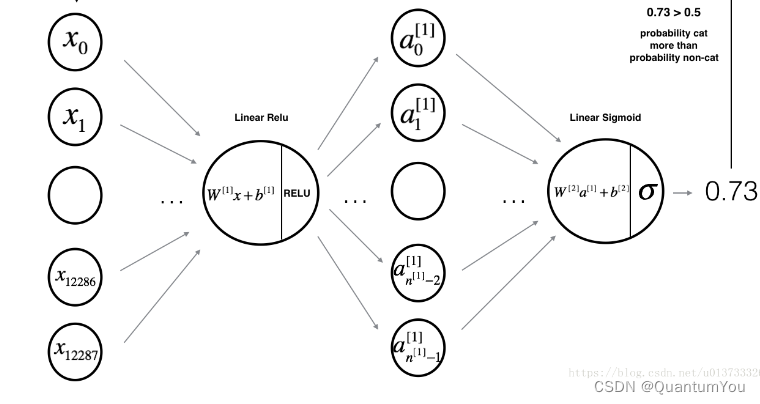
对于一个两层的神经网络结构而言，模型结构是线性->ReLU->线性->sigmod函数。

说明：

• 随机初始化权重矩阵。 确保准确的维度，使用np.random.randn（shape）* 0.01。
• 将偏差初始化为0。 使用np.zeros（shape）。\

def initialize_parameters(n_x,n_h,n_y):
    """
    此函数是为了初始化两层网络参数而使用的函数。
    参数：
        n_x - 输入层节点数量
        n_h - 隐藏层节点数量
        n_y - 输出层节点数量
    
    返回：
        parameters - 包含你的参数的python字典：
            W1 - 权重矩阵,维度为（n_h，n_x）
            b1 - 偏向量，维度为（n_h，1）
            W2 - 权重矩阵，维度为（n_y，n_h）
            b2 - 偏向量，维度为（n_y，1）

    """
    W1 = np.random.randn(n_h, n_x) * 0.01
    b1 = np.zeros((n_h, 1))
    W2 = np.random.randn(n_y, n_h) * 0.01
    b2 = np.zeros((n_y, 1))
    
    #使用断言确保我的数据格式是正确的
    assert(W1.shape == (n_h, n_x))
    assert(b1.shape == (n_h, 1))
    assert(W2.shape == (n_y, n_h))
    assert(b2.shape == (n_y, 1))
    
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    
    return parameters  

拓展关于L 层神经网络初始化

3、正向传播

前向传播有以下三个步骤

• LINEAR
• LINEAR - >ACTIVATION，其中激活函数将会使用ReLU或Sigmoid。
• [LINEAR - > RELU] ×（L-1） - > LINEAR - > SIGMOID（整个模型）

线性正向传播模块（向量化所有示例）使用如下LateX公式

$$Z^{[l]}={\mathbf{W}}^{[l]\top }{\mathbf{A}}^{[l-1]}+{\mathbf{b}}^{[l]}$$

def linear_forward(A,W,b):
    """
    实现前向传播的线性部分。

    参数：
        A - 来自上一层（或输入数据）的激活，维度为(上一层的节点数量，示例的数量）
        W - 权重矩阵，numpy数组，维度为（当前图层的节点数量，前一图层的节点数量）
        b - 偏向量，numpy向量，维度为（当前图层节点数量，1）

    返回：
         Z - 激活功能的输入，也称为预激活参数
         cache - 一个包含“A”，“W”和“b”的字典，存储这些变量以有效地计算后向传递
    """
    
    Z = np.dot(W,A) + b

    assert(Z.shape == (W.shape[0],A.shape[1]))
    cache = (A,W,b)
     
    return Z,cache

3、线性激活部分

• 为了更方便，我们将把两个功能（线性和激活）分组为一个功能（LINEAR-> ACTIVATION）。 因此，我们将实现一个执行LINEAR前进步骤，然后执行ACTIVATION前进步骤的功能。

$$A^{[l]}=\sigma ({\mathbf{Z}}^{[l]})=\frac{1}{1+e^{-{\mathbf{Z}}^{[l]}}}$$

$${\mathbf{A}}^{[l]}=\text{ReLU}({\mathbf{Z}}^{[l]})=\max (0,{\mathbf{Z}}^{[l]})$$

def linear_activation_forward(A_prev,W,b,activation):
    """
    实现LINEAR-> ACTIVATION 这一层的前向传播

    参数：
        A_prev - 来自上一层（或输入层）的激活，维度为(上一层的节点数量，示例数）
        W - 权重矩阵，numpy数组，维度为（当前层的节点数量，前一层的大小）
        b - 偏向量，numpy阵列，维度为（当前层的节点数量，1）
        activation - 选择在此层中使用的激活函数名，字符串类型，【"sigmoid" | "relu"】

    返回：
        A - 激活函数的输出，也称为激活后的值
        cache - 一个包含“linear_cache”和“activation_cache”的字典，我们需要存储它以有效地计算后向传递
    """
    
    if activation == "sigmoid":
        Z, linear_cache = linear_forward(A_prev, W, b)
        A, activation_cache = sigmoid(Z)
    elif activation == "relu":
        Z, linear_cache = linear_forward(A_prev, W, b)
        A, activation_cache = relu(Z)
    
    assert(A.shape == (W.shape[0],A_prev.shape[1]))
    cache = (linear_cache,activation_cache)
    
    return A,cache

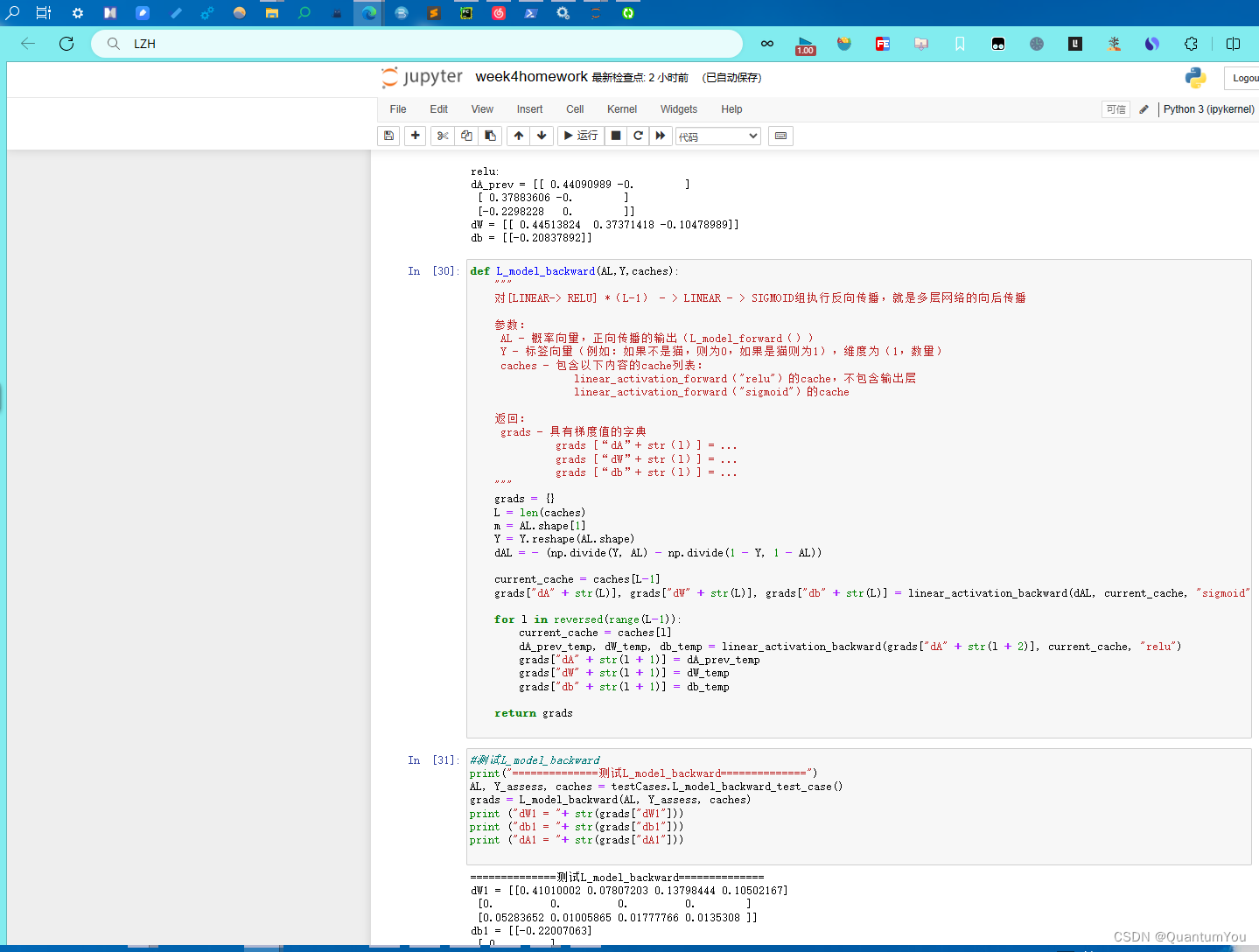
拓展关于L 层模型

• 为了方便实现L层神经网络，你将需要一个函数来复制前一个函数（使用RELU的linear_activation_forward）L-1 次，以及复制带有SIGMOID的linear_activation_forward。

实现细节：

• 使用你先前编写的函数
• 使用for循环复制[LINEAR-> RELU]（L-1）次
• 不要忘记在“cache”列表中更新缓存。 要将新值 c添加到list中，可以使用list.append©。

4、损失函数

使用以下公式计算交叉熵损失

$$Loss=-\frac{1}{m}\sum _{i=1}^m[y_i\log ({\hat{y}}_i)+(1-y_i)\log (1-{\hat{y}}_i)]$$

def compute_cost(AL,Y):
    """
    实施等式（4）定义的成本函数。

    参数：
        AL - 与标签预测相对应的概率向量，维度为（1，示例数量）
        Y - 标签向量（例如：如果不是猫，则为0，如果是猫则为1），维度为（1，数量）

    返回：
        cost - 交叉熵成本
    """
    m = Y.shape[1]
    cost = -np.sum(np.multiply(np.log(AL),Y) + np.multiply(np.log(1 - AL), 1 - Y)) / m
        
    cost = np.squeeze(cost)
    assert(cost.shape == ())

    return cost

5、反向传播

实现反向传播 线性部分

def linear_backward(dZ,cache):
    """
    为单层实现反向传播的线性部分（第L层）

    参数：
         dZ - 相对于（当前第l层的）线性输出的成本梯度
         cache - 来自当前层前向传播的值的元组（A_prev，W，b）

    返回：
         dA_prev - 相对于激活（前一层l-1）的成本梯度，与A_prev维度相同
         dW - 相对于W（当前层l）的成本梯度，与W的维度相同
         db - 相对于b（当前层l）的成本梯度，与b维度相同
    """
    A_prev, W, b = cache
    m = A_prev.shape[1]
    dW = np.dot(dZ, A_prev.T) / m
    db = np.sum(dZ, axis=1, keepdims=True) / m
    dA_prev = np.dot(W.T, dZ)
    
    assert (dA_prev.shape == A_prev.shape)
    assert (dW.shape == W.shape)
    assert (db.shape == b.shape)
    
    return dA_prev, dW, db

实现反向传播 激活部分

def linear_activation_backward(dA,cache,activation="relu"):
    """
    实现LINEAR-> ACTIVATION层的后向传播。
    
    参数：
         dA - 当前层l的激活后的梯度值
         cache - 我们存储的用于有效计算反向传播的值的元组（值为linear_cache，activation_cache）
         activation - 要在此层中使用的激活函数名，字符串类型，【"sigmoid" | "relu"】
    返回：
         dA_prev - 相对于激活（前一层l-1）的成本梯度值，与A_prev维度相同
         dW - 相对于W（当前层l）的成本梯度值，与W的维度相同
         db - 相对于b（当前层l）的成本梯度值，与b的维度相同
    """
    linear_cache, activation_cache = cache
    if activation == "relu":
        dZ = relu_backward(dA, activation_cache)
        dA_prev, dW, db = linear_backward(dZ, linear_cache)
    elif activation == "sigmoid":
        dZ = sigmoid_backward(dA, activation_cache)
        dA_prev, dW, db = linear_backward(dZ, linear_cache)
    
    return dA_prev,dW,db

拓展关于L 层模型

$$Z^{[L]}={\nabla }_{{\mathbf{A}}^{[L]}}\text{Loss}\odot g^{\prime }({\mathbf{Z}}^{[L]})$$

$$W^{[L]}=\frac{1}{m}d{\mathbf{Z}}^{[L]}{\mathbf{A}}^{[L-1]\top }$$

$$d{\mathbf{b}}^{[L]}=\frac{1}{m}\sum _{i=1}^{m}d{Z}_i^{[L]}$$

6、更新参数

说明：对于 L = 1,2,3……L 使用梯度下降更新每个 W^[l] 和b^[l] 的参数。

权重更新

$$W^{[l]}={\mathbf{W}}^{[l]}-\alpha d{\mathbf{W}}^{[l]}$$

偏置更新

$$b^{[l]}={\mathbf{b}}^{[l]}-\alpha d{\mathbf{b}}^{[l]}$$

其中 α 是学习率。

def update_parameters(parameters, grads, learning_rate):
    """
    使用梯度下降更新参数
    
    参数：
     parameters - 包含你的参数的字典
     grads - 包含梯度值的字典，是L_model_backward的输出
    
    返回：
     parameters - 包含更新参数的字典
                   参数[“W”+ str（l）] = ...
                   参数[“b”+ str（l）] = ...
    """
    L = len(parameters) // 2 #整除
    for l in range(L):
        parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * grads["dW" + str(l + 1)]
        parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * grads["db" + str(l + 1)]
        
    return parameters

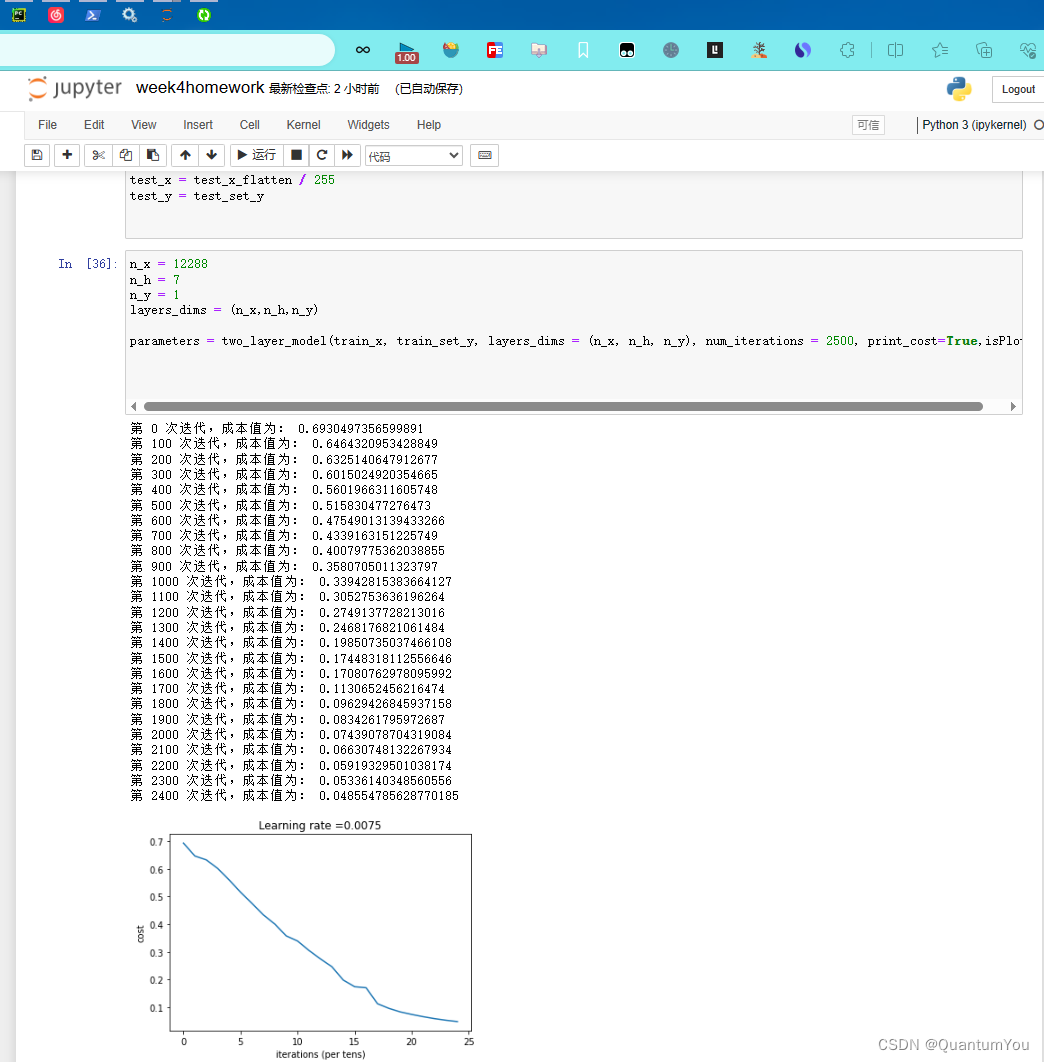
7、搭建两层神经网络

def two_layer_model(X,Y,layers_dims,learning_rate=0.0075,num_iterations=3000,print_cost=False,isPlot=True):
    """
    实现一个两层的神经网络，【LINEAR->RELU】 -> 【LINEAR->SIGMOID】
    参数：
        X - 输入的数据，维度为(n_x，例子数)
        Y - 标签，向量，0为非猫，1为猫，维度为(1,数量)
        layers_dims - 层数的向量，维度为(n_y,n_h,n_y)
        learning_rate - 学习率
        num_iterations - 迭代的次数
        print_cost - 是否打印成本值，每100次打印一次
        isPlot - 是否绘制出误差值的图谱
    返回:
        parameters - 一个包含W1，b1，W2，b2的字典变量
    """
    np.random.seed(1)
    grads = {}
    costs = []
    (n_x,n_h,n_y) = layers_dims
    
    """
    初始化参数
    """
    parameters = initialize_parameters(n_x, n_h, n_y)
    
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    
    """
    开始进行迭代
    """
    for i in range(0,num_iterations):
        #前向传播
        A1, cache1 = linear_activation_forward(X, W1, b1, "relu")
        A2, cache2 = linear_activation_forward(A1, W2, b2, "sigmoid")
        
        #计算成本
        cost = compute_cost(A2,Y)
        
        #后向传播
        ##初始化后向传播
        dA2 = - (np.divide(Y, A2) - np.divide(1 - Y, 1 - A2))
        
        ##向后传播，输入：“dA2，cache2，cache1”。 输出：“dA1，dW2，db2;还有dA0（未使用），dW1，db1”。
        dA1, dW2, db2 = linear_activation_backward(dA2, cache2, "sigmoid")
        dA0, dW1, db1 = linear_activation_backward(dA1, cache1, "relu")
        
        ##向后传播完成后的数据保存到grads
        grads["dW1"] = dW1
        grads["db1"] = db1
        grads["dW2"] = dW2
        grads["db2"] = db2
        
        #更新参数
        parameters = update_parameters(parameters,grads,learning_rate)
        W1 = parameters["W1"]
        b1 = parameters["b1"]
        W2 = parameters["W2"]
        b2 = parameters["b2"]
        
        #打印成本值，如果print_cost=False则忽略
        if i % 100 == 0:
            #记录成本
            costs.append(cost)
            #是否打印成本值
            if print_cost:
                print("第", i ,"次迭代，成本值为：" ,np.squeeze(cost))
    #迭代完成，根据条件绘制图
    if isPlot:
        plt.plot(np.squeeze(costs))
        plt.ylabel('cost')
        plt.xlabel('iterations (per tens)')
        plt.title("Learning rate =" + str(learning_rate))
        plt.show()
    
    #返回parameters
    return parameters

惯用预测方法

• 神经网络的预测代码是用于根据已经训练好的模型参数，对新的、未见过的数据进行预测或分类的代码。预测代码通常位于神经网络的实现之后，并且在模型训练完成之后使用。以下是预测代码的主要作用：

加载模型参数：预测代码首先加载在训练过程中学习到的模型参数，这些参数包括各层的权重$$\mathbf{W}$$和偏置$$\mathbf{b}$$

-前向传播：使用加载的模型参数，预测代码执行前向传播过程。这意味着它将新的输入数据通过神经网络的每一层，计算每一层的输出，直到得到最终的预测结果。

输出预测结果：前向传播完成后，神经网络将输出预测结果。对于分类问题，这通常是概率分布，表示输入数据属于每个类别的可能性；对于回归问题，这通常是一个具体的数值。

def predict(X, y, parameters):
    """
    该函数用于预测L层神经网络的结果，当然也包含两层
    
    参数：
     X - 测试集
     y - 标签
     parameters - 训练模型的参数
    
    返回：
     p - 给定数据集X的预测
    """
    
    m = X.shape[1]
    n = len(parameters) // 2 # 神经网络的层数
    p = np.zeros((1,m))
    
    #根据参数前向传播
    probas, caches = L_model_forward(X, parameters)
    
    for i in range(0, probas.shape[1]):
        if probas[0,i] > 0.5:
            p[0,i] = 1
        else:
            p[0,i] = 0
    
    print("准确度为: "  + str(float(np.sum((p == y))/m)))
        
    return p

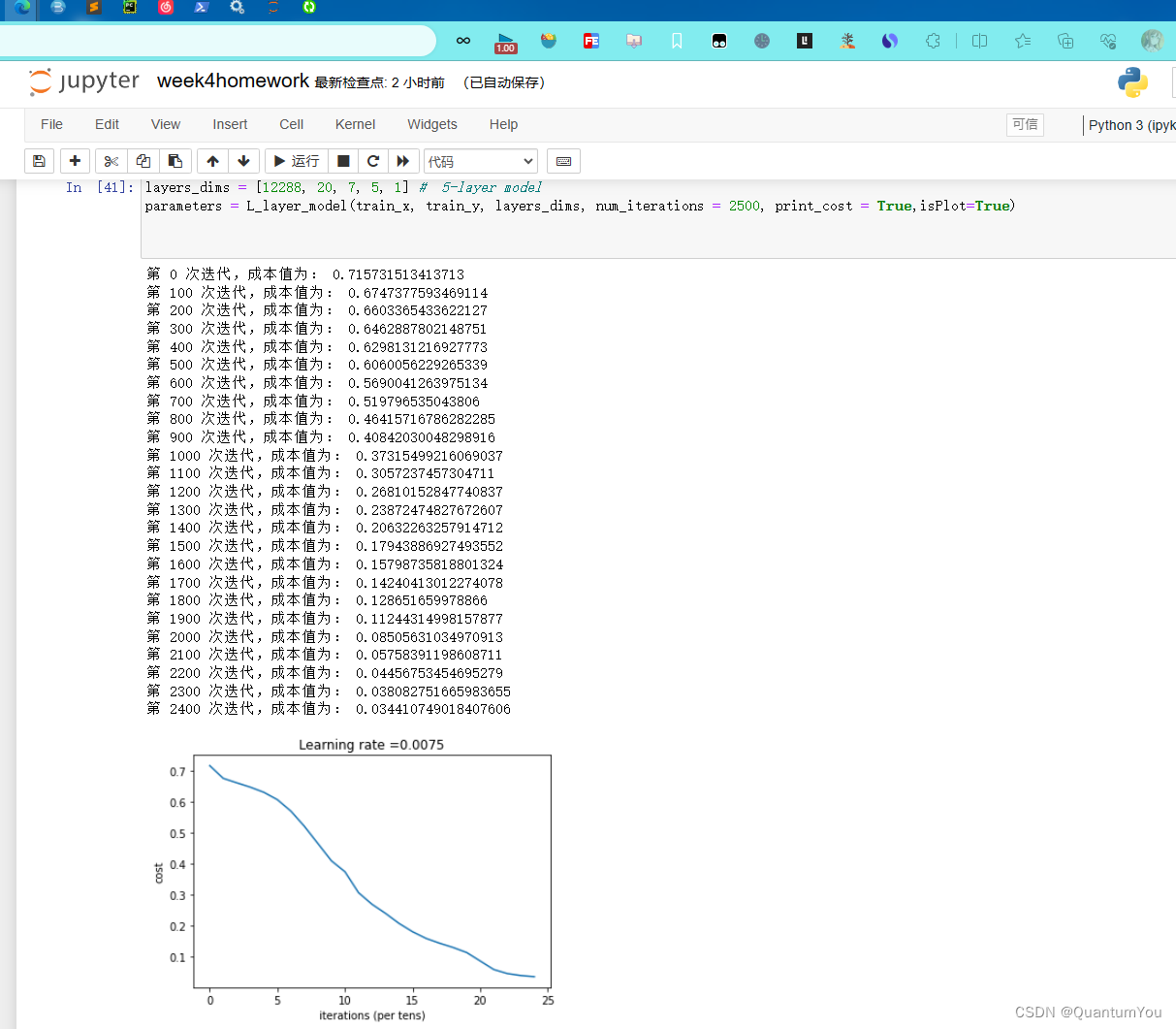
8、搭建L层神经网络及优化

def L_layer_model(X, Y, layers_dims, learning_rate=0.0075, num_iterations=3000, print_cost=False,isPlot=True):
    """
    实现一个L层神经网络：[LINEAR-> RELU] *（L-1） - > LINEAR-> SIGMOID。
    
    参数：
	    X - 输入的数据，维度为(n_x，例子数)
        Y - 标签，向量，0为非猫，1为猫，维度为(1,数量)
        layers_dims - 层数的向量，维度为(n_y,n_h,···,n_h,n_y)
        learning_rate - 学习率
        num_iterations - 迭代的次数
        print_cost - 是否打印成本值，每100次打印一次
        isPlot - 是否绘制出误差值的图谱
    
    返回：
     parameters - 模型学习的参数。 然后他们可以用来预测。
    """
    np.random.seed(1)
    costs = []
    
    parameters = initialize_parameters_deep(layers_dims)
    
    for i in range(0,num_iterations):
        AL , caches = L_model_forward(X,parameters)
        
        cost = compute_cost(AL,Y)
        
        grads = L_model_backward(AL,Y,caches)
        
        parameters = update_parameters(parameters,grads,learning_rate)
        
        #打印成本值，如果print_cost=False则忽略
        if i % 100 == 0:
            #记录成本
            costs.append(cost)
            #是否打印成本值
            if print_cost:
                print("第", i ,"次迭代，成本值为：" ,np.squeeze(cost))
    #迭代完成，根据条件绘制图
    if isPlot:
        plt.plot(np.squeeze(costs))
        plt.ylabel('cost')
        plt.xlabel('iterations (per tens)')
        plt.title("Learning rate =" + str(learning_rate))
        plt.show()
    return parameters

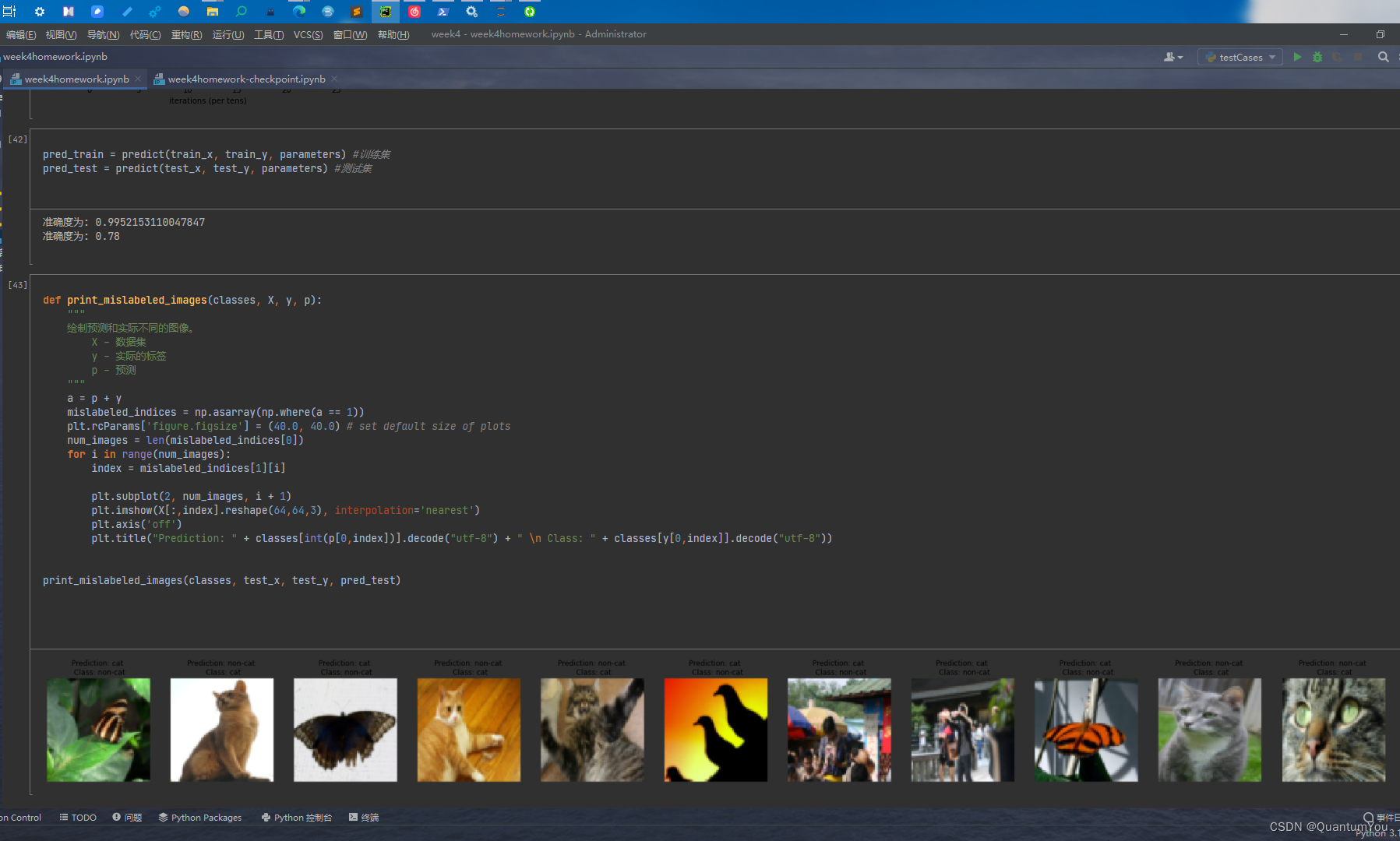
打印出被错误分类的图像，也就是预测标签和实际标签不一致的图像

1. 函数定义:

def print_mislabeled_images(classes, X, y, p):

定义一个函数print_mislabeled_images，它接受四个参数：classes（类别的名称列表），X（数据集），y（实际的标签），p（预测标签）。

2. 文档字符串:

"""
	绘制预测和实际不同的图像。
	    X - 数据集
	    y - 实际的标签
	    p - 预测
"""

这是函数的文档字符串，简要描述了函数的功能和参数。

3. 计算预测和实际标签不同的索引:

a = p + y
mislabeled_indices = np.asarray(np.where(a == 1))

这里首先通过p + y计算预测标签和实际标签的和。对于预测错误的样本，这个和应为1（一个为0，另一个为1）。然后，使用np.where找到所有和为1的索引，并将这些索引转换为numpy数组。

4. 设置默认图形大小:

plt.rcParams['figure.figsize'] = (40.0, 40.0)

使用matplotlib的rcParams设置默认的图形大小为40x40。

5. 获取错误分类的图像数量:

num_images = len(mislabeled_indices[0])

由于mislabeled_indices是一个元组，其中第一个元素是满足条件的索引数组，所以这里获取这个数组的长度，即错误分类的图像数量。

6. 遍历错误分类的索引，并显示图像:

for i in range(num_images):
    index = mislabeled_indices[1][i]
    plt.subplot(2, num_images, i + 1)
    plt.imshow(X[:,index].reshape(64,64,3), interpolation='nearest')
    plt.axis('off')
    plt.title("Prediction: " + classes[int(p[0,index])].decode("utf-8") + " \n Class: " + classes[y[0,index]].decode("utf-8"))

这部分代码遍历所有错误分类的索引，并使用matplotlib的subplot函数在一张图上绘制多个子图。每个子图显示一个错误分类的图像，并标注其预测标签和实际标签。

• index = mislabeled_indices[1][i]：这里似乎有一个小错误。应该是index = mislabeled_indices[0][i]，因为我们想要获取的是第一个元素（索引数组）中的索引。
• plt.imshow(X[:,index].reshape(64,64,3), interpolation='nearest')：显示图像。这里假设X是一个二维数组，其中每列是一个图像的扁平化表示，所以X[:,index]取出了索引为index的图像列，并通过reshape将其恢复为64x64x3的形状（假设图像是64x64像素的RGB图像）。
• plt.axis('off')：关闭坐标轴。
• plt.title(...)：设置子图的标题，显示预测标签和实际标签。

7. 调用函数:

print_mislabeled_images(classes, test_x, test_y, pred_test)

最后，调用这个函数，传入实际的类别名称列表、测试数据集、测试标签和预测标签。