LIME论文简介

LIME的全称为Local Interpretable Model-agnostic Explanations.
LIME
尽管被广泛采用，机器学习模型仍然主要是黑匣子。然而，了解预测背后的原因对于评估信任非常重要，如果一个人计划根据预测采取行动，或者在选择是否部署新模型时，信任是基础。这种理解还提供了对模型的洞察力，可用于将不可信的模型或预测转换为可信的模型。

在这项工作中，作者提出了 LIME，这是一种新颖的解释技术，通过在预测局部学习可解释模型，以可解释和忠实的方式解释任何分类器的预测。作者还提出了一种通过以非冗余方式呈现具有代表性的个体预测及其解释来解释模型的方法，将任务构建为子模块优化问题。

通过解释文本（例如随机森林）和图像分类（例如神经网络）的不同模型来展示这些方法的灵活性。作者通过新的实验（包括模拟实验和人类受试者）在需要信任的各种场景中展示解释的效用：决定一个人是否应该相信一个预测，在模型之间进行选择，改进一个不可信的分类器，以及确定为什么一个分类器不应该被信任。
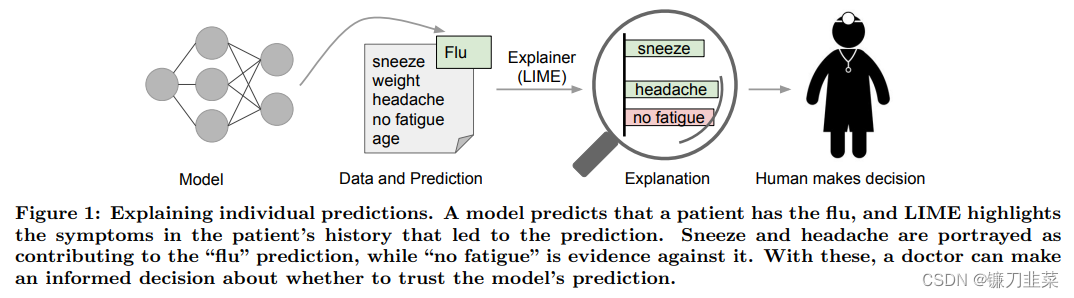
Explaining individual predictions

LIME算法原理

LIME的想法很简单，希望使用简单的模型来对复杂的模型进行解释。这里简单的模型可以是线性模型，因为我们可以通过查看线性模型的系数大小来对模型进行解释。在这里, LIME只会对每一个样本进行解释(explain individual predictions).

LIME会产生一个新的数据集（这个数据集我们是通过对某一个样本数据进行变换得到），接着在这个新的数据集上，我们训练一个简单模型(容易解释的模型), 我们希望简单模型在新数据集上的预测结果和复杂模型在该数据集上的预测结果是相似的。可以将我们的问题表达为下面的表达式：
$\text{explanation}(x)=\text{arg}\min_{g\in G}L(f,g,\pi_x)+\Omega (g)$
其中：

$f$ 表示原始的模型，即需要解释的模型
$g$ 表示简单的模型， $G$ 是简单模型的一个集合，例如所有可能的线性模型。
$\pi_x$ 表示新数据集中的数据 $x^{'}$ 与原始数据 $x$ 的距离
$\Omega(g)$ 表示模型 $g$ 的复杂程度。

希望原始模型 $f$ 与新模型 $g$ 预测值之间的误差是小的。简单来说，可以通过下面的式子来衡量两个式子预测值之间的差：
$\mathcal{L}(f, g, w^y)=\sum_{i=1}^N w^y(z_i)(f(z_i)-g(z'_i))^2$
于是整个LIME的步骤如下(即训练模型 $g$ 的步骤):
①选择想要解释的变量x；
②对数据集中的数据进行扰动得到新的数据，同时计算出黑盒模型对这些新的数据的预测值；
③对这些新的sample求出权重，这个权重是这些数据点与我们要解释的数据之间的距离；
④根据上面新的数据集，预测值和权重，训练出模型 $g$ ；
⑤通过对模型 $g$ 来对模型 $f$ 在x点附近进行解释。

那么我们如何对数据集进行扰动来得到新的数据, 对于表格数据, 我们可以分别扰动每一个特征, 从一个正态分布(均值和方差为这个特征的均值和方差)中进行随机抽样. 这样做会有一个问题, 即不是从我们要解释的数据为中心进行采样, 而是从整个数据集的中心进行采样. (LIME samples are not taken around the instance of interest, but from the training data’s mass center, which is problematic.)

通过一张图片来对上面的过程进行解释(这张图片是上面第一个参考链接中的).
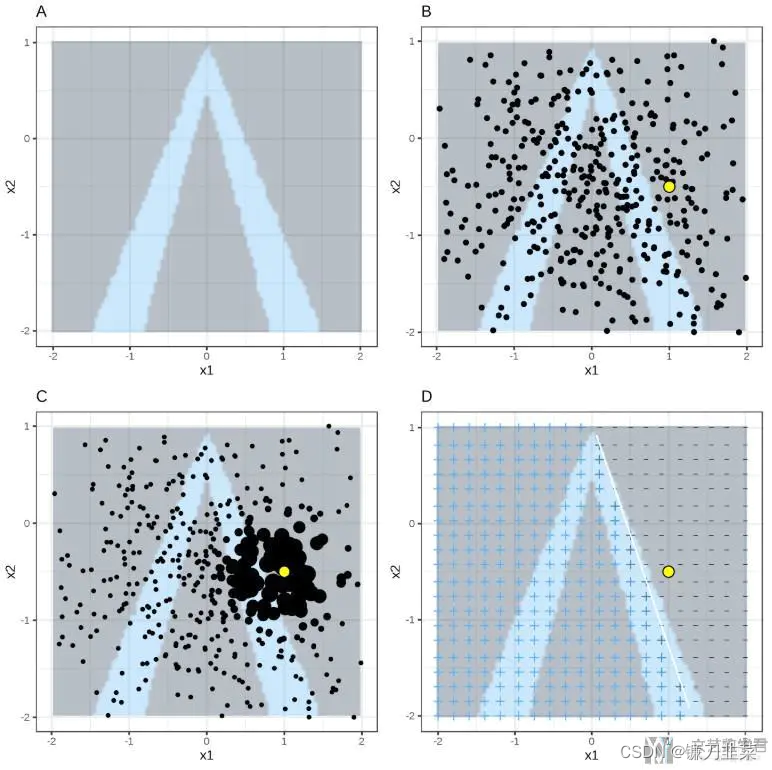
对数据集进行扰动
图A表示: 随机森林的分类结果, 颜色深的为一类, 颜色浅的为一类; 图B表示: 通过对特征进行扰动得到的新的数据集；图C表示: 对每一个数据进行加权；图D表示: 对简单的模型进行求解。

存在的问题: 定义我们要解释的点的周围是困难的.

LIME算法要点

LIME (Ribeiro et al。2016)是一种解释黑盒估计量预测的算法:

根据我们将要解释的例子生成一个假的数据集。
使用黑盒估计器为生成的数据集中的每个示例获取目标值(例如，类概率)。
训练一个新的白盒估计器，使用生成的数据集和生成的标签作为训练数据。这意味着我们正在尝试创建一个估计器，它的工作原理与黑盒估计器相同，但是更容易检查。它不必在全局范围内工作得很好，但是它必须在接近原始示例的区域内很好地近似黑盒模型。
要表示“接近原始示例的区域”，用户必须为生成的数据集中的示例提供距离/相似度度量。然后根据训练数据与原始样本之间的距离进行加权——样本越远，训练数据对白盒估计器权值的影响越小。
通过这个白盒估计器的权重来解释原来的例子。
白盒分类器的预测质量显示了它对黑盒分类器的近似程度。如果质量低，那么解释就不可信。

LIME的注意事项

如果白盒估计器在生成的数据集上获得高分，并不一定意味着它可以被信任——这也可能意味着生成的数据集过于简单和统一，或者用户提供的相似性度量为大多数示例分配了非常低的值，因此“接近原始示例的区域”太小而不有趣。
假数据集生成是主要问题；它在很大程度上是特定于任务的。所以 LIME 可以与任何黑盒分类器一起工作，但用户可能需要为每个数据集编写特定的代码。检查模型权重有一个相反的权衡：它适用于任何任务，但必须为每种估计器类型编写检查代码。
eli5.lime为文本数据（删除随机词）和任意数据（使用核密度估计采样）提供数据集生成实用程序。
对于文本数据，eli5 还提供了 eli5.lime.TextExplainer，它汇集了所有 LIME 步骤并允许解释文本分类器； 它仍然需要对分类器做出假设才能生成有效的假数据集。
相似性度量对结果有巨大影响。通过选择不同大小的邻域，可以得到相反的解释。

LIME的代码实现

有一个由 LIME 作者实现的 LIME：https://github.com/marcotcr/lime，所以 eli5.lime 应该被视为替代品。在撰写本文时，eli5.lime 与规范的 LIME 实现有一些差异：

eli5 支持来自多个库的许多白盒分类器，可以将它们中的任何一个与 LIME 一起使用；
eli5 支持使用核密度估计生成数据集，以确保生成的数据集看起来与原始数据集相似；
为了解释概率分类器的预测，eli5 默认使用另一个分类器，使用交叉熵损失进行训练，而标准库在概率输出上拟合回归模型。

对Pytorch搭建的模型进行解释

首先是描述Pytorch的完整训练的过程。这里使用Iris dataset作为数据集来搭建一个多分类的网络.

import pandas as pd
import numpy as np
from sklearn import datasets

from sklearn.preprocessing import StandardScaler
%matplotlib inline

导入Pytorch相关库：

import torch
import torch.nn as nn
import torch.utils.data as Data

数据导入：

iris_datas = datasets.load_iris()
df = pd.concat([pd.DataFrame(iris_datas.data), pd.DataFrame(iris_datas.target)], axis=1)
df.columns = iris_datas.feature_names+['target']
df = df.sample(frac=1) # 打乱顺序
df.head()

数据导入
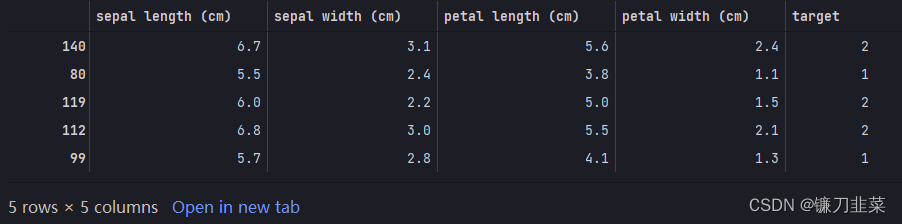
数据处理，包括数据集划分、数据标准化，并将数据转换为tensor类型：

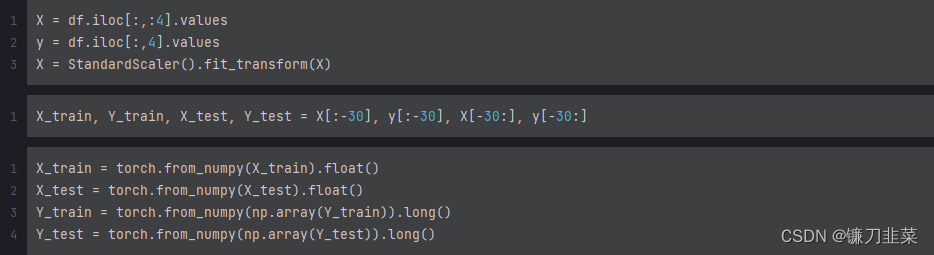
构建dataset和dataloader：

batch_size = 10
train_dataset = Data.TensorDataset(X_train, Y_train)
test_dataset = Data.TensorDataset(X_test, Y_test)

# Data Loader
train_loader = torch.utils.data.DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset=test_dataset, batch_size=batch_size, shuffle=True)

构建网络模型，这里为简单起见，使用全连接网络：

# 网络的定义
class NeuralNet(nn.Module):
    def __init__(self, input_size, hidden_size, num_classes, n_layers):
        super(NeuralNet, self).__init__()
        layers = []
        for i in range(n_layers):
            layers.append(nn.Linear(hidden_size, hidden_size))
            layers.append(nn.ReLU())
            layers.append(nn.BatchNorm1d(hidden_size))
            layers.append(nn.Dropout(0.3))
        self.inLayer = nn.Linear(input_size, hidden_size)
        self.relu = nn.ReLU()
        self.hiddenLayer = nn.Sequential(*layers)
        self.outLayer = nn.Linear(hidden_size, num_classes)
        self.softmax = nn.Softmax(dim=1)

    def forward(self, x):
        out = self.inLayer(x)
        out = self.relu(out)
        out = self.hiddenLayer(out)
        out = self.outLayer(out)
        out = self.softmax(out)
        return out

接着对上面的网络进行初始化：
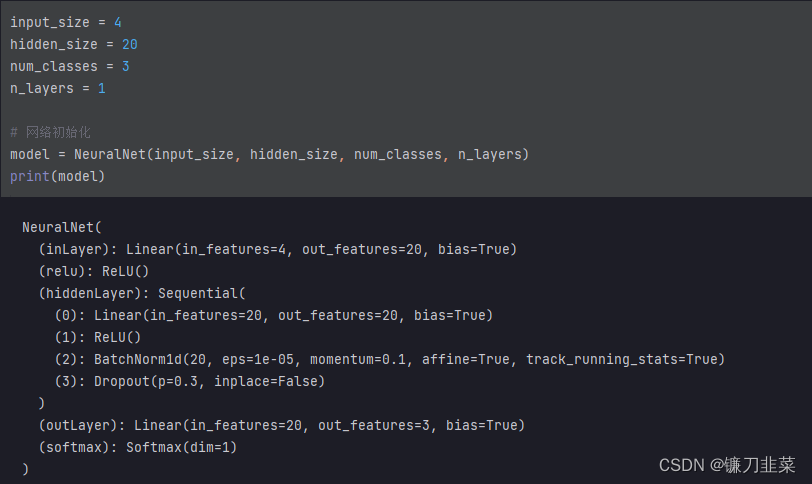
模型初始化
网络训练，包括定义损失函数和优化函数：

# 网络的训练
num_epochs = 30
learning_rate = 0.001

criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)

model.train()
total_step = len(train_loader)
for epoch in range(num_epochs):
    for i, (data, labels) in enumerate(train_loader):
        outputs = model(data)
        loss = criterion(outputs, labels)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        if (i + 1) %5 ==0:
            correct = 0
            total = 0
            _, predicted = torch.max(outputs.data, 1)
            total += labels.size(0)
            correct += sum(predicted == labels).item()
            acc = 100 * correct/total
            print ('Epoch [{}/{}], Step [{}/{}], Accuracy: {}, Loss: {:.4f}'.format(epoch+1, num_epochs, i+1, total_step, acc, loss.item()))
    model.eval()
    with torch.no_grad():
        correct = 0
        total = 0
        for data, labels in test_loader:
            outputs = model(data)
            _, predicted = torch.max(outputs.data, 1)
            total += labels.size(0)
            correct += sum(predicted==labels).item()
        print('Accuracy of the network test dataset: {} %'.format(100 * correct / total))
        print('-'*10)
'''
----------
Epoch [19/30], Step [5/12], Accuracy: 100.0, Loss: 0.6313
Epoch [19/30], Step [10/12], Accuracy: 100.0, Loss: 0.6491
Accuracy of the network test dataset: 93.33333333333333 %
----------
Epoch [20/30], Step [5/12], Accuracy: 100.0, Loss: 0.5853
Epoch [20/30], Step [10/12], Accuracy: 90.0, Loss: 0.6876
Accuracy of the network test dataset: 90.0 %
'''

使用LIME解释Pytorch构建的模型

使用LIME来解释Pytorch的模型主要有下面的几个步骤：

定义预测函数
创建解释器
对某一个样本给出解释

首先定义预测函数：

# 定义预测函数
def batch_predict(data, model=model):
    """
    :param data: 需要预测的数据
    :param model: Pytorch训练的模型，**这里需要有默认的模型**
    :return:
    """
    X_tensor = torch.from_numpy(data).float()
    model.eval()
    device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
    model.to(device)
    X_tensor = X_tensor.to(device)
    logits = model(X_tensor)
    probs = torch.nn.functional.softmax(logits, dim=1)
    return probs.detach().cpu().numpy()

简单测试一下，输入数据, 出来的是每一类的概率.：
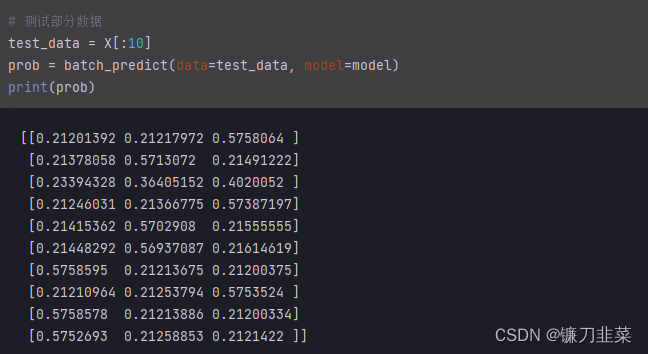
测试预测函数
创建解释器，用来对后面的样本进行解释:

from lime.lime_tabular import LimeTabularExplainer
# 创建解释器
targets = iris_datas.target_names
features_names = iris_datas.feature_names
explainer = LimeTabularExplainer(X, feature_names=features_names, class_names=targets, discretize_continuous=True)

解释某一个样本，这里是对第5个样本进行解释.:

# 解释某个样本
exp = explainer.explain_instance(X[5], batch_predict, num_features=5, top_labels=5)
# 结果可视化
# exp.show_in_notebook(show_table=True, show_all=False) # 代码无效
exp.save_to_file('../Results/exp.html') # 保存为HTML文件，用浏览器打开即可

结果可视化。可视化的内容会包括是某一类的原因(或是不是某一类的原因), 比如对于Iris dataset来说, 会分别给出三张图. 如下所示.

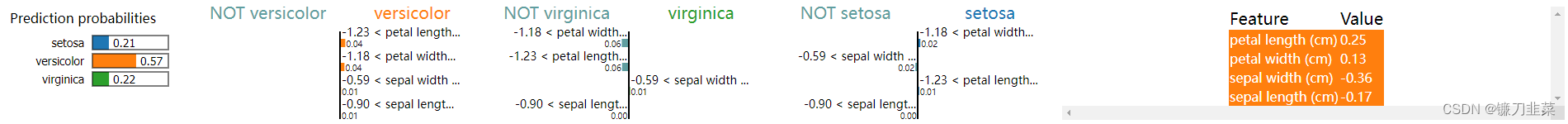
如上图所示, 对于virginica来说, 模型给出了是这个分类的原因, 例如因为petal width>-1.23, 这就是给出了一个模型判断的原因。除了上面的画图方式, 我们还可以使用下面的画图方式, 只画出某一个类别的判断的可能性：
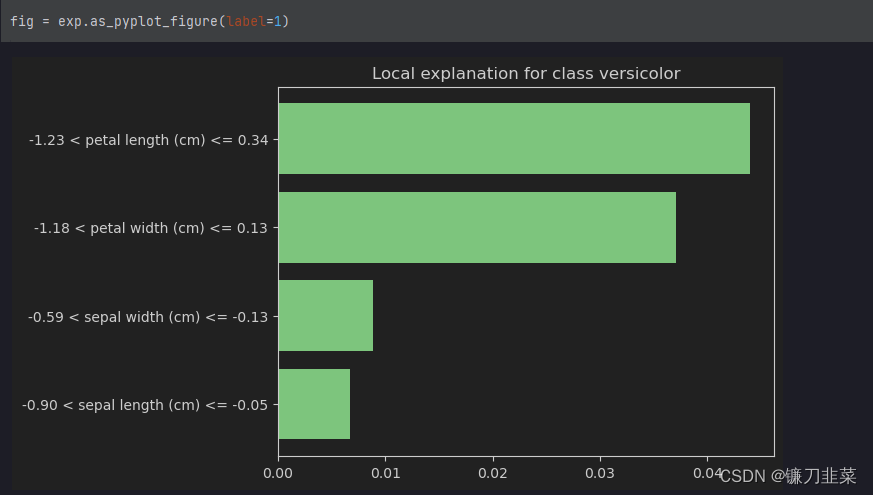
某一个类别的重要性