🔥博客主页: 【小扳_-CSDN博客】
❤感谢大家点赞👍收藏⭐评论✍


文章目录
1.0 BF 算法概述
1.1 BF 算法实际使用
2.0 KMP 算法概述
2.1 KMP 算法实际使用
2.2 相比于 BF 算法实现,KMP 算法的重要思想
2.3 为什么要这样设计?
2.4 next 数组
2.4.1 创建 next 数组原理
2.4.2 创建 next 数组过程
2.5 KMP 算法的实现
1.0 BF 算法概述
是一种基本的暴力搜索算法,也称为穷举算法或暴力匹配算法。BF 算法通过遍历所有可能的解空间来寻找问题的解,虽然效率较低,但在一些简单的问题上仍然具有一定的实用性。
尽管 BF 算法效率较低,但在一些简单的问题上,它仍然可以提供可行的解决方案。在一些小规模的问题、教学示例或者需要快速验证解的情况下,BF 算法可以作为一种简单且直观的解决方法。
1.1 BF 算法实际使用
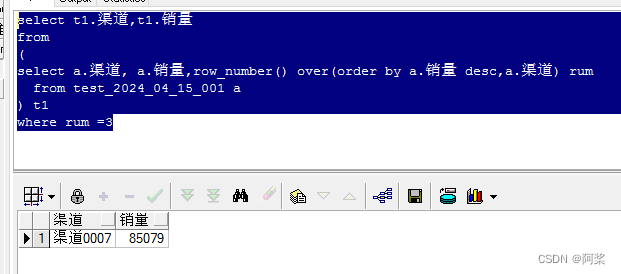
举个例子:用 BF 算法来找到主串 str 中是否存在子串 sub,如果存在,那么子串在主串的具体那个位置。
实现思路:为了实现一个比较严谨的程序,首先对 str 与 sub 进行判断是否为 null 或者长度为 0 。
接着,用变量 i 来记录主串 str 索引下标,用变量 j 来记录子串 sub 索引下标,且用 strLen 来记录主串的长度,用 sunLen 来记录子串的长度。
再接着,用 while 循环,循环比较 str 与 sub 中字符是否相同,如 str.charAt(i) 与 sub.charAt(j) 进行比较,如果两者相同,那么继续往后走 i++ ,j++ ;如果两者不相同,那么对于主串来说,i 需要回到 i = i - j + 1 位置,对于 j 来说, 就要回到原点 j = 0 。
如图:
最后,判断是什么原因导致跳出了循环:
有两个原因:(1)j >= subLen ,则说明了 j 已经比较完毕了,所以主串中存在子串,位置位于:(i - j)。(2)i > strLen ,则说明,即使 i 都走完了, j 还没走完,那么主串中不存在该子串。
代码如下:
public class demo1 { //暴力解法 public static void main(String[] args) { String str = "abbccccfffrreytur"; String sub = "tu"; bf(str,sub); } public static void bf(String str, String sub){ if (str == null || sub == null){ System.out.println("对象为 null"); return; } if (str.length() == 0 || sub.length() == 0){ System.out.println("长度不合法!!!!"); return; } //记录主串下标 int i = 0; //主串长度 int strLen = str.length(); //记录子串下标 int j = 0; //子串长度 int subLen = sub.length(); while (i < strLen && j < subLen){ if (str.charAt(i) == sub.charAt(j)){ i++; j++; }else { //如果不相同了,那么 i 就要回头再来找,而对于 j 就要重头开始了 i = i - j + 1; j = 0; } } if (subLen <= j){ System.out.println("找到子串再主串的位置了:" + (i-j) + " 到 " + (i-1)); }else { System.out.println("没找到!!!!"); } } }
2.0 KMP 算法概述
是一种高效的字符串匹配算法,用于在一个主串中查找一个模式串的出现位置。KMP 算法的核心思想是利用已匹配的信息来尽量减少不必要的比较,从而提高匹配效率。
KMP 算法的时间复杂度为 O(m+n),其中 m 是主串的长度,n 是模式串的长度。相比于 BF 暴力匹配算法,KMP 算法具有更高的效率,尤其在处理大规模文本匹配时表现优异。
简单来说,KMP 算法比 BF 算法有更高的效率,是 BF 一个升级的算法。
2.1 KMP 算法实际使用
同样继续用到 BF 算法的例子。
举个例子:用 BF 算法来找到主串 str 中是否存在子串 sub,如果存在,那么子串在主串的具体那个位置。
用变量 i 来记录主串 str 索引下标,用变量 j 来记录子串 sub 索引下标,且用 strLen 来记录主串的长度,用 sunLen 来记录子串的长度。
2.2 相比于 BF 算法实现,KMP 算法的重要思想
对于 i 来说:i 不后退,i 一直进行的是 i++ ,即使遇到 str.charAt(i) != sub.charAt(j) ,i 也不会后退。
对于 j 来说:当字符都相同 str.charAt(i) == sub.charAt(j) 时,那么 j++ ;当字符不相同 str.charAt(i) != sub.charAt(j) 时,那么 j 会回退到指定的位置,不一定是 0 索引位置。(在 BF 算法中 j 当遇到不相同的时候,一定会回退到 0 索引位置处)
2.3 为什么要这样设计?
为了在主串与子串匹配的时候,提高效率。
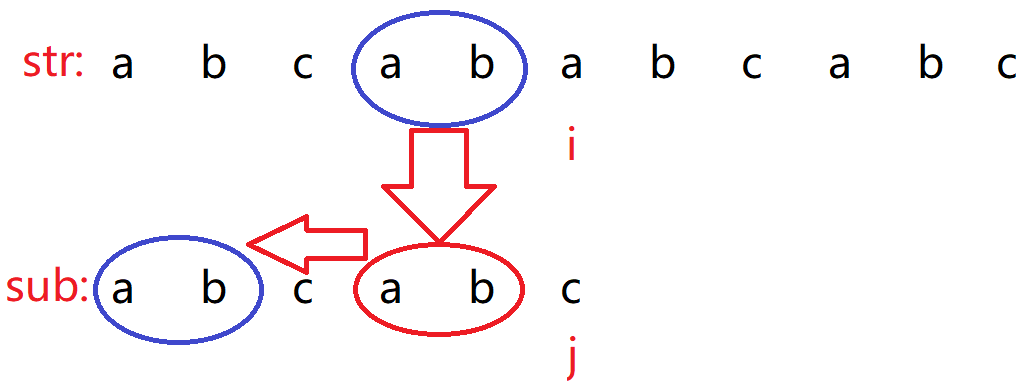
如图:
如果按照 BF 算法来设计,那么 i 就会回到索引为 1 位置 b 处,而 j 就要回到索引为 0 位置 a 处。
而对于 KMP 算法设计来说,当两个字符不相同的时候,i 不用后退,j 不一定退回到索引为 0 处,假设 j 退回到索引为 2 位置 c 处。
先观察两个圈的位置,从当 j 回到索引为 2 位置 c 处,可以发现子串前面的两个字符与主串的对应的两个字符是一样的,这样就避免了 BF 算法的冗余的比较。
到底原理是为啥呢?
发现 a != c 了,但是前面部分肯定是相同的,不然都不会来到此处,那么主串 str 就想着尝试去在 sub 其他位置(除了当前红圈位置的 ab )中找到与主串前部分有没有相同的子字符串,当前就找到了(子串蓝圈部分),那么既然前部分 ab 相同,就不需要比较了,当前比较的是蓝色圈后一个字符是否相同。
当前来看,是不相同的。那么 i 继续保持不动,j 继续跳到指定的位置,那么假设跳到索引为 0 处的位置。
发现 str.charAt(i) == sub.charAt(j) 时,i++,j++ ,一直到结束为止。
2.4 next 数组
刚刚上面提到了当遇到 str.charAt(i) == sub.charAt(j) 时,i 保持不变而 j 会跳到指定的位置。而这个指定的位置就是 j 对应下标的位置 j = next[j] 。
2.4.1 创建 next 数组原理
举个例子来演示
初始化为:
next 数组中,索引为 0 和索引为 1 分别设置为 -1 和 0。
接着,到字符 c 的索引下标了,先判断字符 c 前面的字符串有无以 a 开头且以 b 结尾的两个不重复的字符串。显然,这里就两个字符 a b ,没有找到相同的以 a 开头,且以 b 结尾的两个相同且可以不完全重叠的字符串。那么字符 c 的 next 对应就为 0 。
再接着,到子串索引为 3 处的字符 a ,先判断该字符 a 前面的字符串 a b c 有无以 a 开头且以 c 结尾的两个相同且不完全重叠的字符串,很显然是没有的,同样对应该 next 为 0 。
再接着,到子串索引为 4 处的字符 b ,先判断 b 字符前面的 a b c a 无以 a 开头且以 a 结尾的两个相同且不完全重叠的字符串。这次发现了存在这样的两个字符串,a 与 a ,长度为 1 。那么对应到 next 数组为 1 。
再接着,到子串索引为 5 处的字符 c ,先判断 c 字符前面的 a b c a b 有无以 a 开头且以 b 结尾的两个不相同且不完全重叠的字符串。可以明显的发现 ab 与 ab 满足,长度为 2 ,那么对应到 next 数组中为 2 。
这样 next 数组就创建完毕了。
再来讲讲具体如何使用 next 数组。
接着上一个例子:
此时 str.charAt(i) != sub.charAt(j) ,那么 i 保持不动,j 就会根据 next 数组来回到指定的地方,此时 j = next[j] 。因为 j 的值为 5,在 next[5] 中所对应的索引为 2 。
j 回到索引为 2 处,继续比较 sub.charAt(j) 与 str.charAt(i) 是否相同。如果不相同,i 继续保持不动,j 继续根据 next 数组来给 j 赋值指定的索引;如果相同,那么 i++,j++。
以上这样情况 a != c ,就要 j 重新赋值 j = next[j] ,则 j = 0 。
j 回到索引 0 之后,继续比较 sub.charAt(j) 与 str.charAt(i) 是否相同。如果相同,i++,j++ ;如果不相同,i 保持不动,j 就要根据 next 数组来找到对应的值 j = next[j] 。
以上该情况是相同的,那么直接 i++,j++ 即可。
补充:当 j = 0 时,发现 sub.charAt(0) 与 str.charAt(i) 还是不相同时,j 根据 next 数组来获取值 j = next[j] 则 j = -1 。这种情况需要特殊考虑,当 j == -1 时,不能再继续比较了,因为会出现数组越界问题,那么该情况应该进行 i++,j++ 操作处理。
2.4.2 创建 next 数组过程
1)初始化 next 数组:将 next 数组的第一个元素 next[0] 设置为 -1,next[1] 设置为 0。
2)遍历模式串:从第二个位置开始(即 i=2),依次计算每个位置 i 处的 next 值。
3)计算 next 值:具体思路:定义 int k = 0, 从 i = 2 开始,判断子串 sub[i - 1] 与 k 是否相同,如果相同,则 next[i] = k,i++,k++;如果不相同,则 k = next[k] ,直到找到 sub[i-1] 与 k 相同为止,或者 k == -1 为止。
举个例子:
判断 sub.charAt(k) 与 sub.charAt(i-1) 是否相同,a 与 b很显然不相同,那么 k = next[k] 则 k = -1 ,那么 k == -1 的时候,next[i] = k+1,i++,j++ 。
此时 k = 0,i = 3 。
判断 sub.charAt(k) 与 sub.charAt(i-1) 是否相同,a 与 c 很显然不相同,那么 k = next[k] 则 k = -1 ,那么 k == -1 的时候,next[i] = k+1,i++,j++ 。
此时 k = 0,i = 4 。
判断 sub.charAt(k) 与 sub.charAt(i-1) 是否相同,a 与 a 是相同的,那么 next[i] = k+1,i++,k++ 。
此时 next[4] = 1,k = 1,i = 5 。
判断 sub.charAt(k) 与 sub.charAt(i-1) 是否相同,b 与 b 是相同的,那么 next[5] = k+1,k++,i++ 。
此时 next[5] = 2,k = 2, i = 5 。
最后 next 数组就创建完毕了。
2.5 KMP 算法的实现
1)在循环过程中,判断主串与子串对应的字符是否相同,如果相同,继续往下比较下去,直到子串遍历完成,说明了主串中存在该子串;如果不相同,记录主串下标的索引保持不变,而记录子串下标的索引需要根据 next 数组来找到相对应的值,接着重新比较子串与主串中字符是否相同,如果相同,继续往下比较;如果不相同,记录子串下标的索引就要继续根据 next 数组来找到指定的位置。
需要注意的是,当子串下标的索引为 -1 的时候,不能继续往下比较了,该情况为特殊情况,需要进行的操作为:主串往后移动一次,子串的索引 + 1 处理。该特殊情况的操作,跟主串下标对应的字符与子串下标对应的字符相同的情况的操作处理是一致的。
2)next 数组的创建,首先初始化 next 数组,next[0] = -1,next[1] = 0 。定义 int k = 0,i = 2 ,判断 sub.charAt(i-1) 与 sub.charAt(k) 是否相同,如果相同,next[i] = k+1,i++,k++ ;如果不相同,k = next[k] 。
需要注意的是,当出现 k == -1 特殊情况的时候,该处理方式为 next[i] = k+1,i++,k++ ,跟 sub.charAt(i-1) 与 sub.charAt(k) 相同处理操作的方式是一致的。
代码如下:
public class demo1 { public static void main(String[] args) { String str = "abcccffggaaffggggkkkllrrr"; String sub = "aaffk"; kmp(str,sub); } public static void kmp(String str,String sub){ if (str == null || sub == null){ System.out.println("str 或者 sub 不合法"); return; } if (str.length() == 0 || sub.length() == 0){ System.out.println(str + " 或者 " + sub + " 长度为 0" ); } //用来记录主串的下标 int i = 0; //记录主串的长度 int strLen = str.length(); //用来记录子串的下标 int j = 0; //记录子串的长度 int subLen = sub.length(); //next 数组,存放的是子串与主串不适配所需要 j 回溯的索引下标,长度为字串的长度 int[] next = new int[subLen]; getNext(next,sub); while (i < strLen && j < subLen){ if ( j == -1 || str.charAt(i) == sub.charAt(j)){ i++; j++; }else { //当不相同的时候,j 需要回溯到指定的地方 j = next[j]; } } //判断退出循环的原因 if (j >= subLen){ System.out.println("找到该主串中子串的位置了:" + (i-j) + " 到 " + (i-1)); }else { System.out.println("没有找到!!!"); } } public static void getNext(int[] next,String sub){ next[0] = -1; next[1] = 0; int i = 2; int k = 0; int len = sub.length(); while (i < len){ if (k == -1 || sub.charAt(i-1) == sub.charAt(k)){ next[i] = k+1; i++; k++; }else { //如果不相同,那么会继续接着找,直到相同为止或者k==-1为止 k = next[k]; } } } }











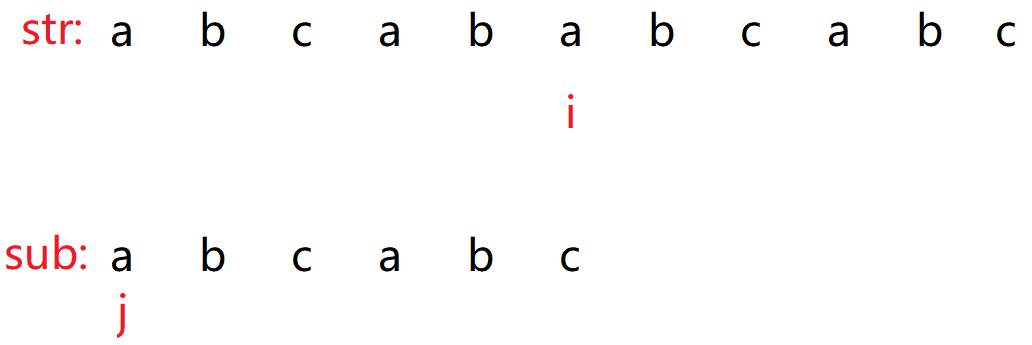














![[阅读笔记1][GPT-3]Language Models are Few-Shot Learners](https://img-blog.csdnimg.cn/direct/fc2a2977c968468aab18f3dc61e8847c.png)