算法拾遗二十四之暴力递归到动态规划二
- 背包问题一
- 优化
- 题目二
- 优化
- 题目三(贴纸拼词)
- 优化
- 题目四:最长公共子序列
- 优化
背包问题一

weights[i]和values[i]的值都是大于等于0的,不存在负数的情况。
可以从尝试入手,改动态规划,常见从左往右依次尝试的模型
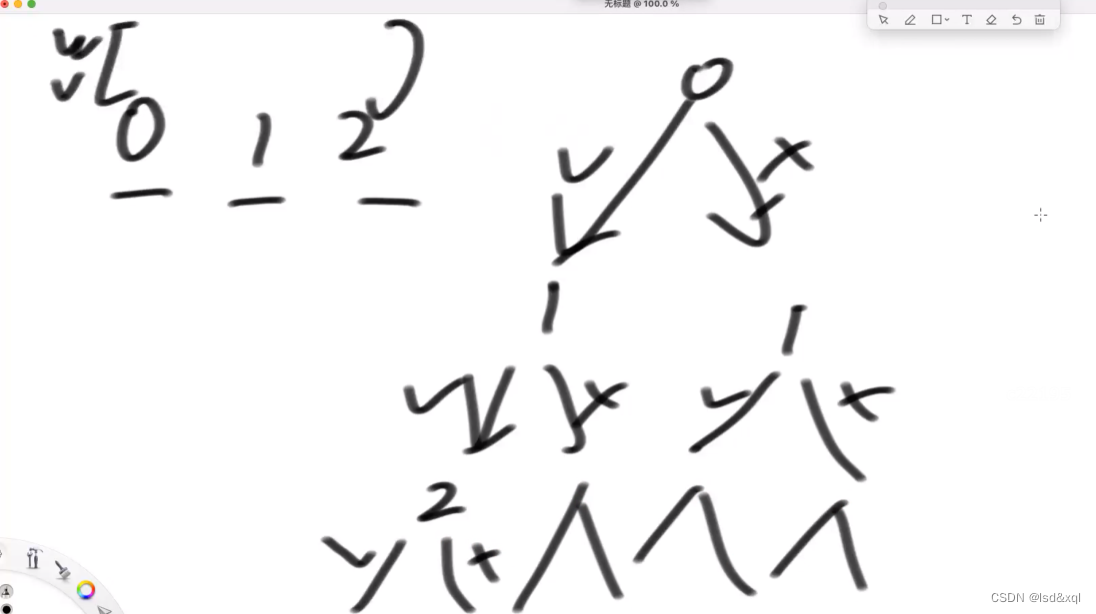
假设有0,1,2三个货物,分别有其重量和价值,我们通过从左往右,0号货物在要的时候【不要的时候】1号货物在要的时候【不要的时候】2号货物在要的时候【不要的时候】,每个分支都走,那么就能找到最大值,因为我们暴力枚举了。
//所有的货,重量和价值,都在w和v数组里
//为了方便,其中没有负数
//bag背包容量,不能超过这个载重
//返回:不超重的情况下,能够得到的最大价值
public static int maxValue(int[] w, int[] v, int bag) {
if (w == null || v == null || w.length != v.length || w.length == 0) {
return 0;
}
//尝试函数
return process(w, v, 0, bag);
}
/**
* @param w
* @param v
* @param index 当前考虑到了index号货物,index及其后面的所有货物都可以自由选择,
* 返回最大价值,所作的选择不能超过背包容量
* @param bag
* @return
*/
public static int process(int[] w, int[] v, int index, int bag) {
//bag 不写成<=0是因为可能weight=0但是value!=0
if (bag < 0) {
return -1;
}
//越界位置,没有货物
if (index == w.length) {
return 0;
}
// index 没到最后,有货,index位置的货
// bag有空间
//不要当前的货,走所有的分支
int p1 = process(w, v, index + 1, bag);
//要当前的货,走所有的分支
int p2 = 0;
int next = process(w, v, index + 1, bag - w[index]);
//看是否是一个无效解,要我后续有效才加
if (next != -1) {
p2 = v[index] + next;
}
return Math.max(p1, p2);
}
优化
先看暴力递归是否有重复调用,
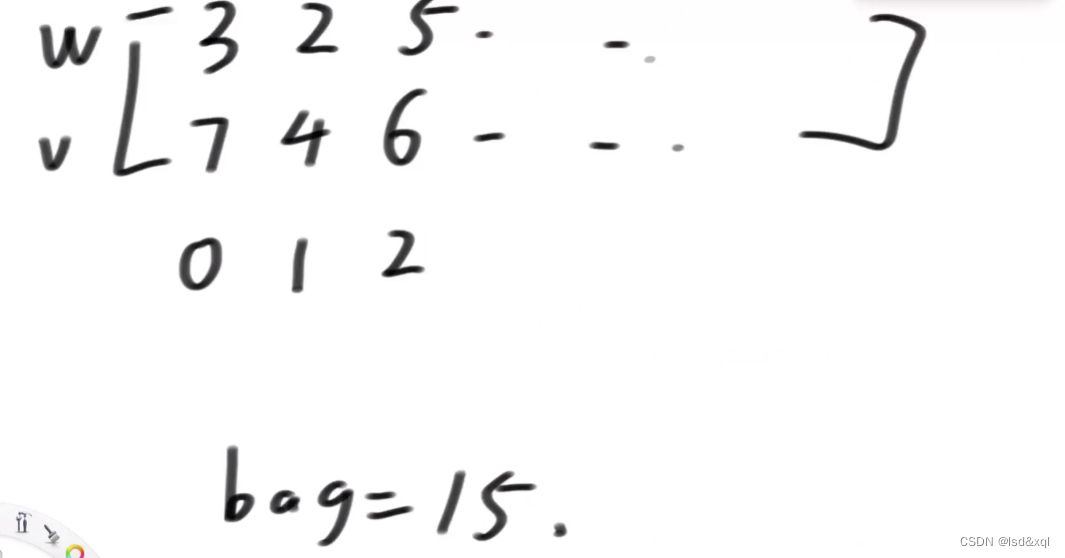
w,v 是固定参数,后面两个参数是可变参数,
首先调用p(0,15)
如果要了0,1但是没有要2号传p(3,10)
如果没要0,1但是要了2号同样是传p(3,10)
重复过程就出现了。
再分析可变参数的变化范围
index 0-N
rest(bag的rest):负-bag
建表:
假设有4个货物,bag=10,如下图:


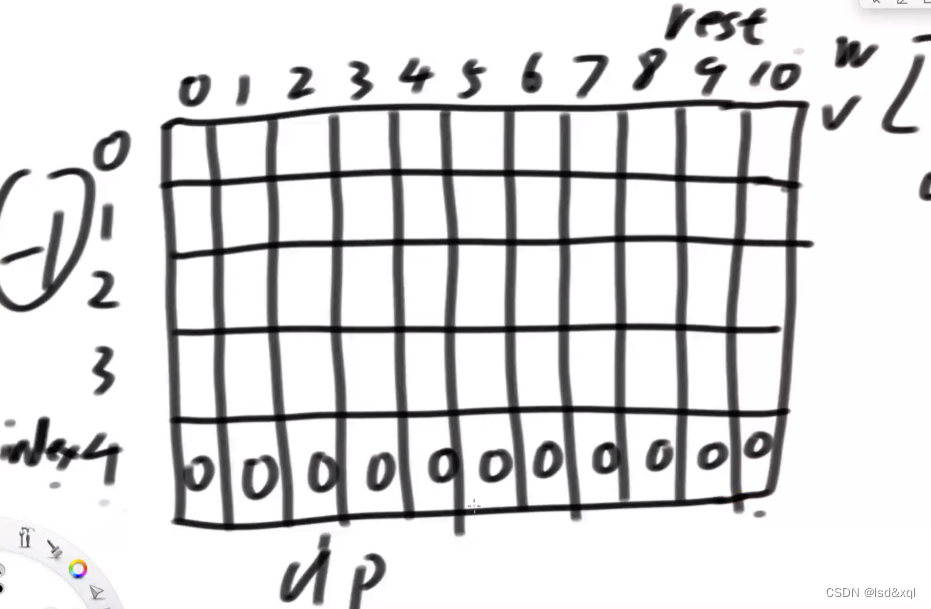
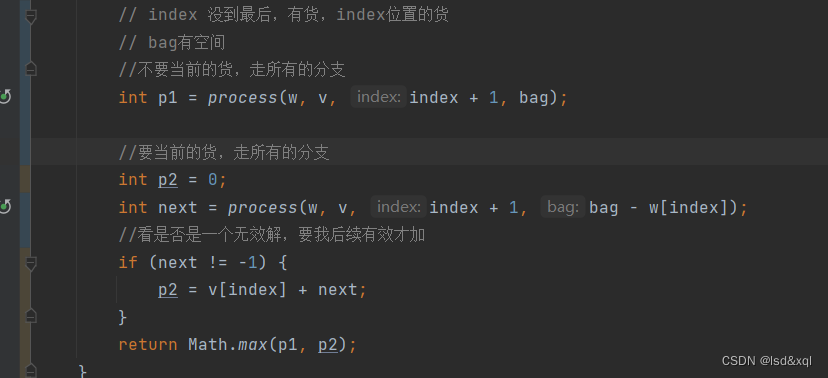
再根据如上代码去推
public static int dp(int[] w, int[] v, int bag) {
if (w == null || v == null || w.length != v.length || w.length == 0) {
return 0;
}
int N = w.length;
//index 0-N
// rest 假设从0到bag
int[][] dp = new int[N + 1][bag + 1];
// 填入dp,看依赖关系
for (int index = N - 1; index >= 0; index--) {
for(int rest = 0 ; rest <= bag;rest++) {
int p1 = dp[index+1][rest];
int p2 = 0;
int next = rest -w[index] < 0 ? -1 : dp[index+1][rest-w[index]];
if(next != -1) {
p2 = v[index] + next;
}
dp[index][rest] = Math.max(p1,p2);
}
}
return dp[0][bag];
}
题目二


如上图,终止条件返回1,是因为我的0位置做了决定是A,我的1位置做了决定是A,2位置做了决定是A,3位置终止返回1,我前面做了决定将111,转换为AAA,我3位置只是搜集一个点数。
如果做的决定单独遇到了0字符,那么说明前面做的决定是错误的。
//str只含有数字字符0-9
//返回多少种转化方案
public static int number(String str) {
if (str == null || str.length() == 0) {
return 0;
}
return process(str.toCharArray(), 0);
}
//str[0..i-1]转化无需过问
//str[i...]去转化,返回有多少种转化方法
public static int process(char[] str, int i) {
if (i == str.length) {
return 1;
}
//i没到最后,说明有字符
if (str[i] == '0') {
return 0;
}
//str[i]!='0'我总是可以做一个决定的
// ,就是让i位置上的字符单转,然后让i+1位置做决定
//可能性一,i单转
int ways = process(str, i + 1);
//可能性二,i位置字符和i+1位置字符共同构成一个字符
if (i + 1 < str.length && (str[i] - '0') * 10 + str[i + 1] - '0' < 27) {
//说明后面有字符
ways+=process(str,i+2);
}
return ways;
}
优化
public static int dp2(String s) {
if (s == null || s.length() == 0) {
return 0;
}
char[] str = s.toCharArray();
int N = str.length;
int[] dp = new int[N + 1];
dp[N] = 1;
for (int i = N - 1; i >= 0; i--) {
if (str[i] != '0') {
int ways = dp[i + 1];
if (i + 1 < str.length && (str[i] - '0') * 10 + str[i + 1] - '0' < 27) {
ways += dp[i + 2];
}
dp[i] = ways;
}
}
return dp[0];
}
题目三(贴纸拼词)
本题测试链接:https://leetcode.com/problems/stickers-to-spell-word

思路:
假设有三种贴纸
“abc”,“bba”,“cck”,
然后要拼成如下串"bbbbaca"
,首先排序"aabbbbc",然后选择贴纸。
第一张贴纸选abc,看最后能有几张,第一张贴纸选bba看最后能有几张贴纸,第一张贴纸选cck,看最后能有几张,因为最终拼成的结果,【答案必在其中,因为肯定有某张贴纸被作为了第一张,所有分支里面最小的那个就是要的结果】
为什么要排序?
为了命中率更高一些
public static int minStickers1(String[] stickers, String target) {
int ans = process1(stickers, target);
//怎么都拼不成target则返回-1
return ans == Integer.MAX_VALUE ? -1 : ans;
}
// 所有贴纸stickers,每一种贴纸都有无穷张
// target
// 返回最少张数
public static int process1(String[] stickers, String target) {
//如果target没剩下东西了【说明之前的决策都分解完了则还需要0张贴纸】
if (target.length() == 0) {
return 0;
}
int min = Integer.MAX_VALUE;
//每一张贴纸都假设是第一张,看target哪些字符能被first搞定,
// 然后剩下的跑下一个流程
for (String first : stickers) {
//每一张贴纸作为第一个串,看还剩下的字符
String rest = minus(target, first);
//跑后续的流程
if (rest.length() != target.length()) {
min = Math.min(min, process1(stickers, rest));
}
}
//如果min是系统最大值,则不让结果加一否则结果加一(加的是第一张卡片,因为第一张在前面的步骤
// 中没算进去)
return min + (min == Integer.MAX_VALUE ? 0 : 1);
}
public static String minus(String s1, String s2) {
char[] str1 = s1.toCharArray();
char[] str2 = s2.toCharArray();
int[] count = new int[26];
for (char cha : str1) {
count[cha - 'a']++;
}
for (char cha : str2) {
count[cha - 'a']--;
}
StringBuilder builder = new StringBuilder();
for (int i = 0; i < 26; i++) {
if (count[i] > 0) {
for (int j = 0; j < count[i]; j++) {
builder.append((char) (i + 'a'));
}
}
}
return builder.toString();
}
说明:
假设有ac和ka两张贴纸,要组成串abc:
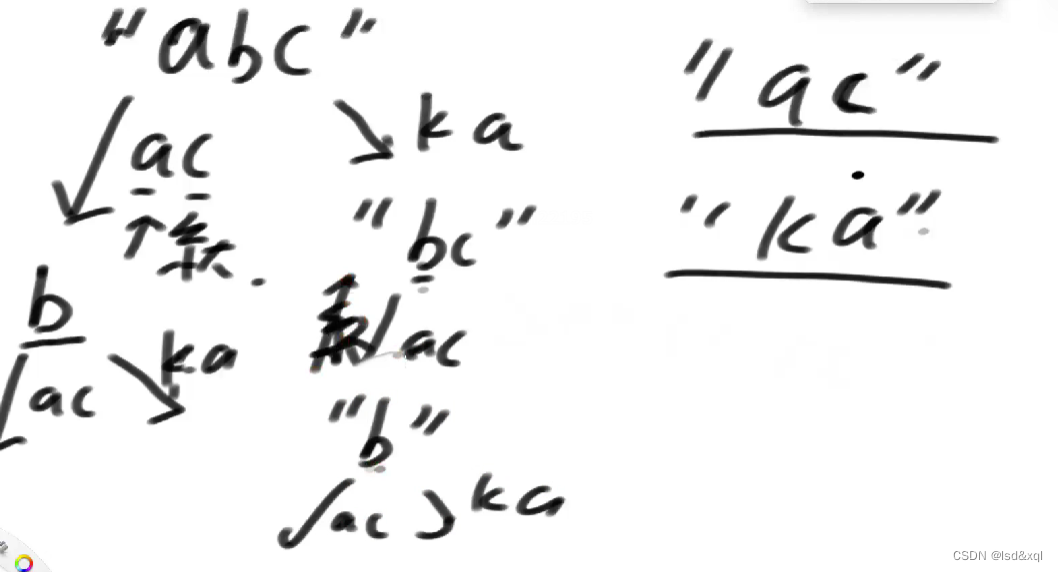
首先选择贴纸ac做第一张,解决了abc里面的ac还剩下一个b,
然后b用ac行吗,发现不行,然后b用ka行吗,发现也不行,返回一个系统最大值回去。
第二步选择ka作为第一张,剩下bc,接下来又用ac行吗,发现不行,b搞不定,用ka行吗,发现还是搞不定b,所以也返回系统最大值回去
优化
假设有如下贴纸:
“acc”,“bbc”,“aaa”
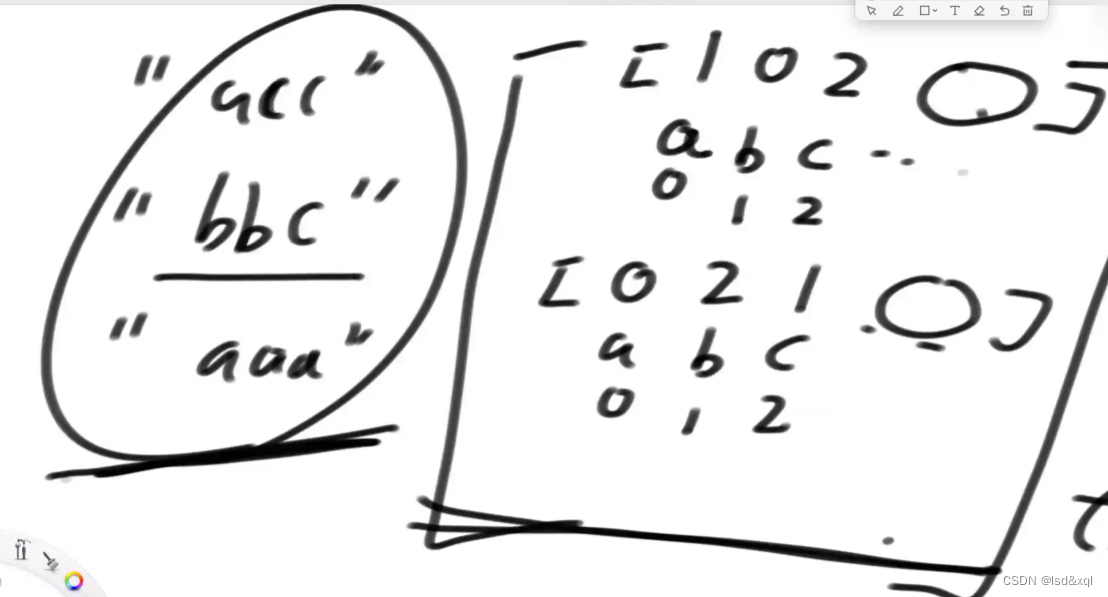
可以做成一个二维数组将字母对应位置标记为词频次数。这样减起来快。
public static int minStickers2(String[] stickers, String target) {
int N = stickers.length;
// 关键优化(用词频表替代贴纸数组)生成词频统计数组
int[][] counts = new int[N][26];
for (int i = 0; i < N; i++) {
char[] str = stickers[i].toCharArray();
for (char cha : str) {
counts[i][cha - 'a']++;
}
}
int ans = process2(counts, target);
return ans == Integer.MAX_VALUE ? -1 : ans;
}
// stickers[i] 数组,当初i号贴纸的字符(词频)统计 int[][] stickers -> 所有的贴纸
// 每一种贴纸都有无穷张
// 返回搞定target的最少张数
public static int process2(int[][] stickers, String t) {
//target0张贴纸
if (t.length() == 0) {
return 0;
}
// target做出词频统计
// target aabbc 2 2 1..
// 0(a) 1(b) 2(c)..
char[] target = t.toCharArray();
int[] tcounts = new int[26];
for (char cha : target) {
tcounts[cha - 'a']++;
}
int N = stickers.length;
int min = Integer.MAX_VALUE;
for (int i = 0; i < N; i++) {
// 尝试第一张贴纸是谁
int[] sticker = stickers[i];
// 最关键的优化(重要的剪枝!这一步也是贪心!)【所有分支中必须含有第一个字符的分支才跑后续流程】
//举例:有目标串aaabbbck,然后有贴纸bbc,cck,kkb,bab,只有bab能第一次进来,剪枝成立
//原来我的最优答案可能出现好几回现在我的最优答案可能就只出现一次
if (sticker[target[0] - 'a'] > 0) {
StringBuilder builder = new StringBuilder();
for (int j = 0; j < 26; j++) {
if (tcounts[j] > 0) {
int nums = tcounts[j] - sticker[j];
for (int k = 0; k < nums; k++) {
builder.append((char) (j + 'a'));
}
}
}
//剩余字符调下一个流程
String rest = builder.toString();
min = Math.min(min, process2(stickers, rest));
}
}
return min + (min == Integer.MAX_VALUE ? 0 : 1);
}
第三种方法:(由于string t是个可变参数,但是不能将其变为严格表结构,因为不知道target有多少可能性,空间可能都爆掉了)
public static int minStickers3(String[] stickers, String target) {
int N = stickers.length;
int[][] counts = new int[N][26];
for (int i = 0; i < N; i++) {
char[] str = stickers[i].toCharArray();
for (char cha : str) {
counts[i][cha - 'a']++;
}
}
HashMap<String, Integer> dp = new HashMap<>();
dp.put("", 0);
int ans = process3(counts, target, dp);
return ans == Integer.MAX_VALUE ? -1 : ans;
}
public static int process3(int[][] stickers, String t, HashMap<String, Integer> dp) {
//target出现过则直接返回
if (dp.containsKey(t)) {
return dp.get(t);
}
char[] target = t.toCharArray();
int[] tcounts = new int[26];
for (char cha : target) {
tcounts[cha - 'a']++;
}
int N = stickers.length;
int min = Integer.MAX_VALUE;
for (int i = 0; i < N; i++) {
int[] sticker = stickers[i];
if (sticker[target[0] - 'a'] > 0) {
StringBuilder builder = new StringBuilder();
for (int j = 0; j < 26; j++) {
if (tcounts[j] > 0) {
int nums = tcounts[j] - sticker[j];
for (int k = 0; k < nums; k++) {
builder.append((char) (j + 'a'));
}
}
}
String rest = builder.toString();
min = Math.min(min, process3(stickers, rest, dp));
}
}
int ans = min + (min == Integer.MAX_VALUE ? 0 : 1);
dp.put(t, ans);
return ans;
}
题目四:最长公共子序列
https://leetcode.cn/problems/longest-common-subsequence/
常见dp模型:
从左往右尝试模型
范围尝试模型(AB玩家拿牌)
样本对应模型(以样本的结尾作为讨论可能性的基础)
业务限制模型

假设str1从0到i位置,str2假设从0到j位置,str1和str2的最长公共子序列是多少。
思路:
根据结尾讨论可能性
public static int longestCommonSubsequence1(String s1, String s2) {
if (s1 == null || s2 == null || s1.length() == 0 || s2.length() == 0) {
return 0;
}
char[] str1 = s1.toCharArray();
char[] str2 = s2.toCharArray();
// 尝试
return process1(str1, str2, str1.length - 1, str2.length - 1);
}
// str1[0...i]和str2[0...j],这个范围上最长公共子序列长度是多少?
// 可能性分类:
// a) 最长公共子序列,一定不以str1[i]字符结尾、也一定不以str2[j]字符结尾(a和bc的可能性重叠了,故不写入,省掉一次遍历)
// b) 最长公共子序列,可能以str1[i]字符结尾、但是一定不以str2[j]字符结尾
// c) 最长公共子序列,一定不以str1[i]字符结尾、但是可能以str2[j]字符结尾
// d) 最长公共子序列,必须以str1[i]字符结尾、也必须以str2[j]字符结尾
// 注意:a)、b)、c)、d)并不是完全互斥的,他们可能会有重叠的情况
// 但是可以肯定,答案不会超过这四种可能性的范围
// 那么我们分别来看一下,这几种可能性怎么调用后续的递归。
// a) 最长公共子序列,一定不以str1[i]字符结尾、也一定不以str2[j]字符结尾
// 如果是这种情况,那么有没有str1[i]和str2[j]就根本不重要了,因为这两个字符一定没用啊
// 所以砍掉这两个字符,最长公共子序列 = str1[0...i-1]与str2[0...j-1]的最长公共子序列长度(后续递归)
// b) 最长公共子序列,可能以str1[i]字符结尾、但是一定不以str2[j]字符结尾
// 如果是这种情况,那么我们可以确定str2[j]一定没有用,要砍掉;但是str1[i]可能有用,所以要保留
// 所以,最长公共子序列 = str1[0...i]与str2[0...j-1]的最长公共子序列长度(后续递归)
// c) 最长公共子序列,一定不以str1[i]字符结尾、但是可能以str2[j]字符结尾
// 跟上面分析过程类似,最长公共子序列 = str1[0...i-1]与str2[0...j]的最长公共子序列长度(后续递归)
// d) 最长公共子序列,必须以str1[i]字符结尾、也必须以str2[j]字符结尾
// 同时可以看到,可能性d)存在的条件,一定是在str1[i] == str2[j]的情况下,才成立的
// 所以,最长公共子序列总长度 = str1[0...i-1]与str2[0...j-1]的最长公共子序列长度(后续递归) + 1(共同的结尾)
// 综上,四种情况已经穷尽了所有可能性。四种情况中取最大即可
// 其中b)、c)一定参与最大值的比较,
// 当str1[i] == str2[j]时,a)一定比d)小,所以d)参与
// 当str1[i] != str2[j]时,d)压根不存在,所以a)参与
// 但是再次注意了!
// a)是:str1[0...i-1]与str2[0...j-1]的最长公共子序列长度
// b)是:str1[0...i]与str2[0...j-1]的最长公共子序列长度
// c)是:str1[0...i-1]与str2[0...j]的最长公共子序列长度
// a)中str1的范围 < b)中str1的范围,a)中str2的范围 == b)中str2的范围
// 所以a)不用求也知道,它比不过b)啊,因为有一个样本的范围比b)小啊!
// a)中str1的范围 == c)中str1的范围,a)中str2的范围 < c)中str2的范围
// 所以a)不用求也知道,它比不过c)啊,因为有一个样本的范围比c)小啊!
// 至此,可以知道,a)就是个垃圾,有它没它,都不影响最大值的决策
// 所以,当str1[i] == str2[j]时,b)、c)、d)中选出最大值
// 当str1[i] != str2[j]时,b)、c)中选出最大值
public static int process1(char[] str1, char[] str2, int i, int j) {
if (i == 0 && j == 0) {
// str1[0..0]和str2[0..0],都只剩一个字符了
// 那如果字符相等,公共子序列长度就是1,不相等就是0
// 这显而易见
return str1[i] == str2[j] ? 1 : 0;
} else if (i == 0) {
// 这里的情况为:
// str1[0...0]和str2[0...j],str1只剩1个字符了,但是str2不只一个字符
// 因为str1只剩一个字符了,所以str1[0...0]和str2[0...j]公共子序列最多长度为1
// 如果str1[0] == str2[j],那么此时相等已经找到了!公共子序列长度就是1,也不可能更大了
// 如果str1[0] != str2[j],只是此时不相等而已,
// 那么str2[0...j-1]上有没有字符等于str1[0]呢?不知道,所以递归继续找
if (str1[i] == str2[j]) {
return 1;
} else {
return process1(str1, str2, i, j - 1);
}
} else if (j == 0) {
// 和上面的else if同理
// str1[0...i]和str2[0...0],str2只剩1个字符了,但是str1不只一个字符
// 因为str2只剩一个字符了,所以str1[0...i]和str2[0...0]公共子序列最多长度为1
// 如果str1[i] == str2[0],那么此时相等已经找到了!公共子序列长度就是1,也不可能更大了
// 如果str1[i] != str2[0],只是此时不相等而已,
// 那么str1[0...i-1]上有没有字符等于str2[0]呢?不知道,所以递归继续找
if (str1[i] == str2[j]) {
return 1;
} else {
return process1(str1, str2, i - 1, j);
}
} else { // i != 0 && j != 0
// 这里的情况为:
// str1[0...i]和str2[0...i],str1和str2都不只一个字符
// 看函数开始之前的注释部分
// p1就是可能性c)
int p1 = process1(str1, str2, i - 1, j);
// p2就是可能性b)
int p2 = process1(str1, str2, i, j - 1);
// p3就是可能性d),如果可能性d)存在,即str1[i] == str2[j],那么p3就求出来,参与pk
// 如果可能性d)不存在,即str1[i] != str2[j],那么让p3等于0,然后去参与pk,反正不影响
int p3 = str1[i] == str2[j] ? (1 + process1(str1, str2, i - 1, j - 1)) : 0;
return Math.max(p1, Math.max(p2, p3));
}
}
优化
改dp:
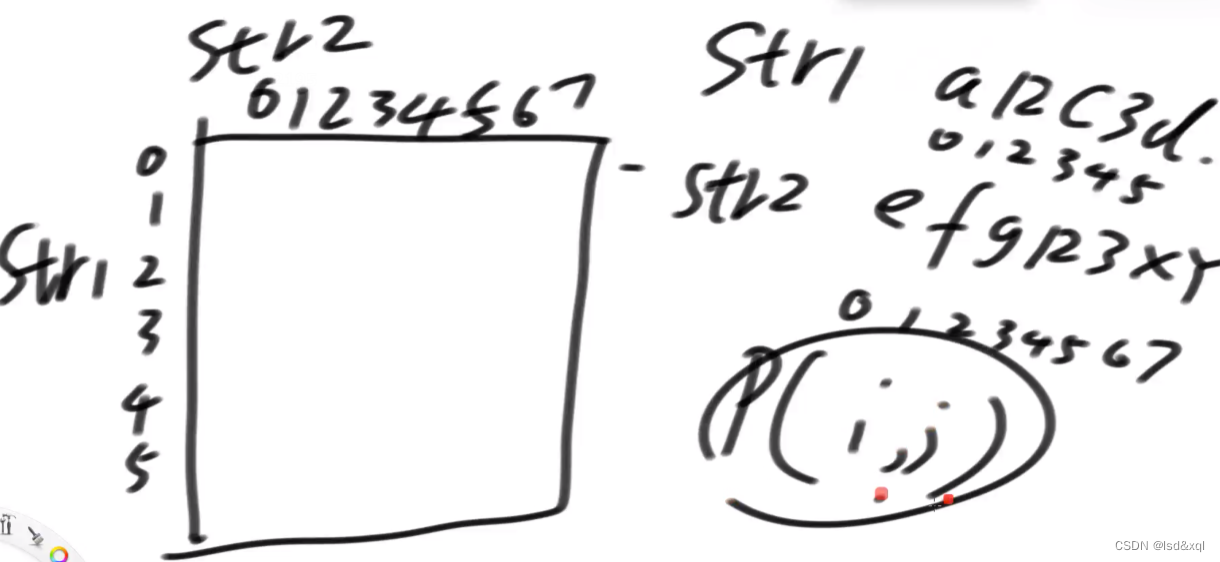
有三个依赖:
process1(str1, str2, i, j - 1);
process1(str1, str2, i - 1, j);
process1(str1, str2, i - 1, j - 1)
改出如下dp:
public static int longestCommonSubsequence3(String s1, String s2) {
if (s1 == null || s2 == null || s1.length() == 0 || s2.length() == 0) {
return 0;
}
char[] str1 = s1.toCharArray();
char[] str2 = s2.toCharArray();
int N = str1.length;
int M = str2.length;
int[][] dp = new int[N][M];
/*
if (i == 0 && j == 0) {
return str1[i] == str2[j] ? 1 : 0;
}
*/
dp[0][0] = str1[0] == str2[0] ? 1 : 0;
/*
else if (i == 0) {
if (str1[i] == str2[j]) {
return 1;
} else {
return process1(str1, str2, i, j - 1);
}
*/
for (int j = 1; j < M; j++) {
dp[0][j] = str1[0] == str2[j] ? 1 : dp[0][j - 1];
}
/*
else if (j == 0) {
if (str1[i] == str2[j]) {
return 1;
} else {
return process1(str1, str2, i - 1, j);
}
}
*/
for (int i = 1; i < N; i++) {
dp[i][0] = str1[i] == str2[0] ? 1 : dp[i - 1][0];
}
for (int i = 1; i < N; i++) {
for (int j = 1; j < M; j++) {
int p1 = dp[i - 1][j];
int p2 = dp[i][j - 1];
int p3 = str1[i] == str2[j] ? (1 + dp[i - 1][j - 1]) : 0;
dp[i][j] = Math.max(p1, Math.max(p2, p3));
}
}
return dp[N-1][M-1];
}
总结:当有一个样本做行,另一个样本做列的时候,就用它的结尾组织可能性,【包含上面代码的a,b,c,d四种情况】

![【系列02】Java流程控制 scanner 选择结构 循环结构语句使用 [有目录]](https://img-blog.csdnimg.cn/5e68d469ab1c4584b0127228f4460473.png)