传送门

题意：

给你n个蜘蛛，每个蜘蛛有自己的腿数，如果某两个蜘蛛可以直接联系，那么这两个蜘蛛的最大公约数就不为1，否则这两只蜘蛛就不能直接联系。现在给你两个蜘蛛的序号i,j问这两只蜘蛛是否可以直接或者通过其他的蜘蛛产生联系？

思路：

因为每两只蜘蛛能够产生联系的条件是GCD(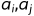)!=1，那么我们可以先预处理一下把

每一只蜘蛛所包含的质数存起来，然后存

每个质数包含那些蜘蛛。

可以直接用试除法（时间有点卡），也可以用线性筛预处理然后遍历

因为他是问能否从i蜘蛛走向j蜘蛛，那么就是问能不能通过i bfs走到 j，

那么可以从起点开始，定义两个状态数组st1（这个质数是否被走过）,st2（这个人是否被走过）

然后从这个蜘蛛开始遍历他的质数，然后从质数开始遍历有多少人可以走，如果可以走而且没被走过就直接push，这样就是一个基本的bfs

但是题目要求要保存蜘蛛走的路径，那么我们可以定义一个数组k，然后在每次push的时候讲路径存起来：

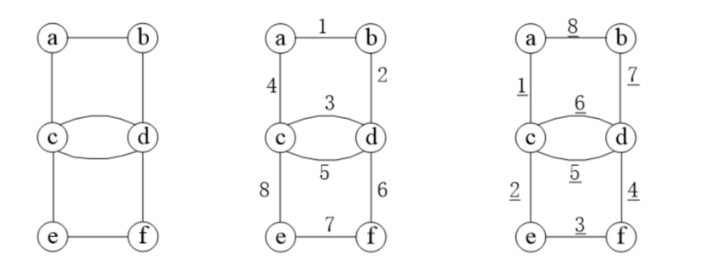
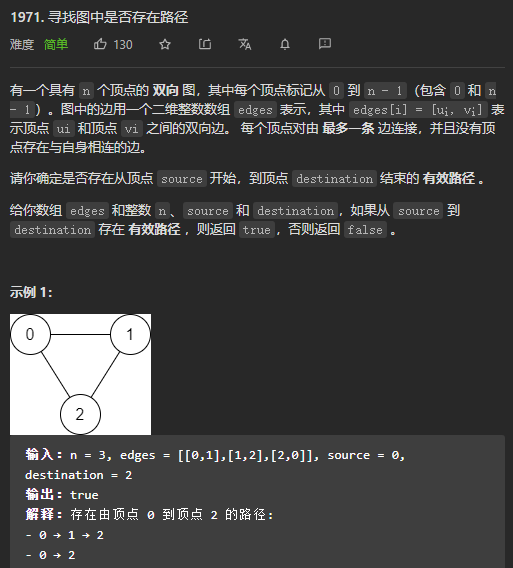
比如

但是这样我们就会发现一个问题，就是a在bfs的时候k[a]会不断发生改变导致最后的k[a]并不是正确的那一个

比如上图：如果是a点走到c点，那么首先k[a]会是b，然后再向他的邻接点走到d就变成了k[a]=d,然后b点走到c,k[b]=c，程序结束，我们可以发现我们应该的序列应该是 a b c ，但是因为后面的bfs会导致我的k[a]是d，序列变成 a d c，为一个错误序列。

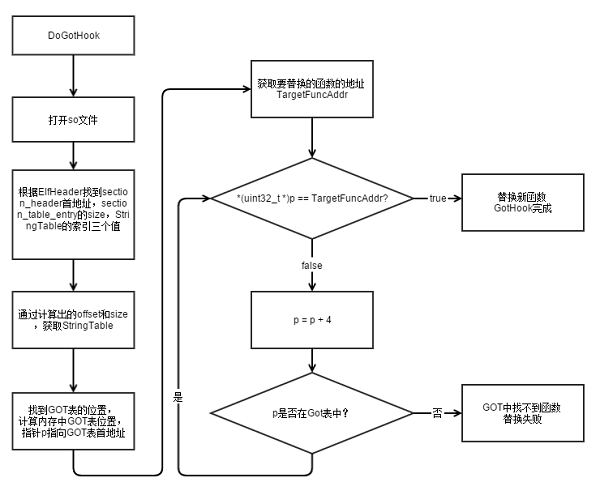
那么为了使序列变成正确的序列，我们可以从终点开始bfs，然后往起始点走，那么k应该如何赋值？

因为是从终点走向起始点：如C->B 那么按照从起点往终点走的话，应该就是k[b]=c;

这样子我们可以发现因为每个点都只会bfs一次，所以k[b]这个地方只会走一遍，那么他的值是不会改变的。如果找到了可以走的路，那么就可以根据k来寻找路径。

具体的就看代码吧！

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <vector>
#include <queue>
#include <map>
#define sc_int(x) scanf("%d", &x)
#define sc_ll(x) scanf("%lld", &x)
#define pr_ll(x) printf("%lld", x)
#define pr_ll_n(x) printf("%lld\n", x)
#define pr_int_n(x) printf("%d\n", x)
#define ll long long
using namespace std;

const int N = 500000 + 100;
int n, m, a, b;
ll s[N];
int p[N], k[N];
bool st[N], st1[N], st2[N];
vector<int> mp[N], pm[N];
int tim=0;
void shai()
{
    int n=3e5;
    st[1]=1;

    for(int i =2;i<=n;i++)
    {
        if(!st[i]) p[++tim]=i;
        for(int j =1;p[j]<=n/i;j++)
        {
            st[i*p[j]]=1;
            if(i%p[j]==0)break;
        }
    }
}


bool bfs()
{
    queue<pair<int, int>> qu;
    qu.push({b, 0});
    st1[b] = 1;
    while (qu.size())
    {
        pair<int, int> lk = qu.front();
        qu.pop();
        int c = lk.first, dis = lk.second;
        for (int i = 0; i < mp[c].size(); i++)
        {
            int kk = mp[c][i]; // 这个质数
            if (st2[kk])
                continue;
            for (int j = 0; j < pm[kk].size(); j++)
            {
                int tt = pm[kk][j]; // 这个人
                if (st1[tt])
                    continue;
                if (tt == a)
                {
                    cout << dis + 2 << endl;
                    //k[c] = b;
                    k[a]=c;
                    return 1;
                }
                //k[c] = tt;
                k[tt]=c;
                st2[kk] = 1, st1[tt] = 1;
                qu.push({tt, dis + 1});
            }
        }
    }
    return 0;
}

void solve()
{

    cin >> n;
    shai();
    for (int i = 1; i <= n; i++)
    {
        sc_ll(s[i]);

        for(int j =1;p[j]<=s[i]/p[j];j++)
        {
            if (s[i] % p[j] == 0)
            {
                while (s[i] % p[j] == 0) s[i] /= p[j];
                mp[i].push_back(p[j]); // 第i个人包含这个质数
                pm[p[j]].push_back(i); // 这个质数包含这个人
            }
        }
        if (s[i] > 1)
        {
            mp[i].push_back(s[i]); // 第i个人包含这个质数
            pm[s[i]].push_back(i); // 这个质数包含这个人
        }        
    }

    cin >> a >> b;
    if (a == b)
    {
        printf("1\n%d", a);
        return;
    }
    if (bfs())
    {
        printf("%d ", a);
        while (k[a] != b)
        {
            printf("%d ", k[a]);
            a = k[a];
        }
        printf("%d\n", b);
    }
    else
        printf("-1");

    return;
}

int main()
{
    solve();
    return 0;
}