目录

题目如下

数据集如下

解题方法

regress 函数

代码实现

得出结果

---

题目如下

        酸雨是降水中各种离子综合作用的结果。实际检测表明:城市降水pH值主要 受酸性离子[SO]、[NO]、[Ca²+]、[NH]影响。下表列出了我国部分城市降水 中[SO]、[NO]、[Ca²⁺]、[NH]的浓度和pH值数据。以[SO]、[NO]、 [Ca²+]、[NH]和组合因子([Ca²+]+[NH]/([SO]+[NO]))为自变量,分别 记为工,2,3,4,25。pH值为因变量y。下表中给出了北京等15个城市的城市降 水pH值和相应影响因素的一组观测值。试对此问题进行回归分析。

数据集如下

城市	x1	x2	x3	x4	x5	pHy
北京	151.8	162.8	154.5	39.5	1.62	6.29
长春	253.6	61.3	156.5	21.2	1.79	6.71
锦州	340.8	123.8	259.2	49.4	1.51	6.32
烟台	289.1	39.1	182.5	22.8	1.6	6.95
平顶山	107.7	138.3	152.3	0.4	1.61	6.29
合肥	110.3	117.3	141.9	31.8	1.31	4.73
苏州	125.3	93.6	200.2	14.4	1.02	4.63
上海	104.3	75.8	153.4	12.6	1.08	4.85
杭州	59.9	68.2	112.3	13.5	1.02	4.84
南宁	26.6	27.7	61.6	4.9	0.82	4.82
桂林	67.2	50	107.2	19.7	0.92	4.83
重庆	127.8	151.1	326.6	27.9	0.79	4.21
贵阳	199.6	174.3	405.2	27.9	0.86	4.23
马鞍山	123	73.7	139.2	15.1	1.27	5.33
广州	175.1	141.1	254.9	33.3	1.1	4.39

解题方法

regress 函数

        在MATLAB中，regress函数被用于进行多元线性回归。它能够估计出回归系数并提供置信区间，还能输出残差以及其他有用的统计信息。这个函数特别适合简单的线性回归分析，当你想要快速地得到回归系数和它们的置信区间时。

        以下是regress函数的基本用法：

b = regress(Y,X); % 基本回归，Y 是因变量，X 是自变量
[b,bint,r,rint,stats] = regress(Y,X,alpha); % 给出详细的输出

这里的输入参数包含：

• Y：因变量，是一个列向量。
• X：自变量，包括一个常数项用于截距。X 是一个矩阵，每一列是一个自变量，行代表观测值。
• alpha：显著性水平，用于定义置信区间（通常是0.05表示95％置信区间）。

输出参数说明：

• b：回归系数的估计值，是一个列向量。
• bint：系数的置信区间，是一个与 b 相同大小的矩阵，每行给出一个系数的置信区间。
• r：残差，是一个列向量，即实际观测值和模型预测值之间的差。
• rint：残差的置信区间，格式与 bint 相同。
• stats：一个包含四个元素的向量:
  • stats(1) R² 统计量（拟合优度）
  • stats(2) F统计量
  • stats(3) F统计量的 p值
  • stats(4) 误差的方差估计

通过检查这些输出，你可以对模型有一个总体的评估。具体来说：

• R² 显示了模型的解释能力，描述自变量解释因变量变异的比例。
• F统计量和它的p值（stats(2)和stats(3)）检验整个模型是否显著。
• 回归系数如果显著非零，相应的自变量对因变量有影响。
• 系数置信区间（bint）有助于理解参数估计的精确度和可靠性。
• 残差（r）和残差置信区间（rint）提供模型适配度的直观信息和观测值可能的误差范围。

        在使用regress函数之前，重要的是要确保数据满足执行线性回归的条件（线性关系、误差项的独立性和正态性、同方差性等）。此外，若你发现数据具有多重共线性等问题时，可能需要使用其他处理方法，例如岭回归或主成分

代码实现

        使用 regress 函数来做线性回归分析，您需要先准备好您的输入矩阵 X（自变量，包含一个常数项以适应截距项）和向量 Y (因变量)。然后，您将能够执行回归分析，并通过分析输出得到关于模型的统计数据。

        由于题目提供的数据已经是结构化的，所以可以直接转换成MATLAB可以处理的格式。

        以下是执行多元线性回归并分析结果的MATLAB代码：

% 首先定义给出的数据
data = [151.8	162.8	154.5	39.5	1.62	6.29;
        253.6	61.3	156.5	21.2	1.79	6.71;
        340.8	123.8	259.2	49.4	1.51	6.32;
        289.1	39.1	182.5	22.8	1.6	    6.95;
        107.7	138.3	152.3	0.4	    1.61	6.29;
        110.3	117.3	141.9	31.8	1.31	4.73;
        125.3	93.6	200.2	14.4	1.02	4.63;
        104.3	75.8	153.4	12.6	1.08	4.85;
        59.9	68.2	112.3	13.5	1.02	4.84;
        26.6	27.7	61.6	4.9	    0.82	4.82;
        67.2	50	    107.2	19.7	0.92	4.83;
        127.8	151.1	326.6	27.9	0.79	4.21;
        199.6	174.3	405.2	27.9	0.86	4.23;
        123	    73.7	139.2	15.1	1.27	5.33;
        175.1	141.1	254.9	33.3	1.1	    4.39];

% 分离自变量X和因变量Y
X = data(:,1:5);
Y = data(:,6);

% 为自变量矩阵X添加常数项列 (必须为1)
X = [ones(size(X,1),1) X];

% 使用 regress函数计算线性回归的参数beta
% regress函数中的 alpha 是用于置信区间的显著性水平，例如 0.05
alpha = 0.05;
[b,bint,r,rint,stats] = regress(Y,X,alpha);

% 输出回归系数和相关统计信息
disp('回归系数 b :');
disp(b);

disp('系数的95%置信区间 bint:');
disp(bint);

disp('残差 r:');
disp(r);

disp('残差的置信区间 rint:');
disp(rint);

disp('统计信息 stats （R方, F统计量, p值,误差方差）:');
disp(stats);

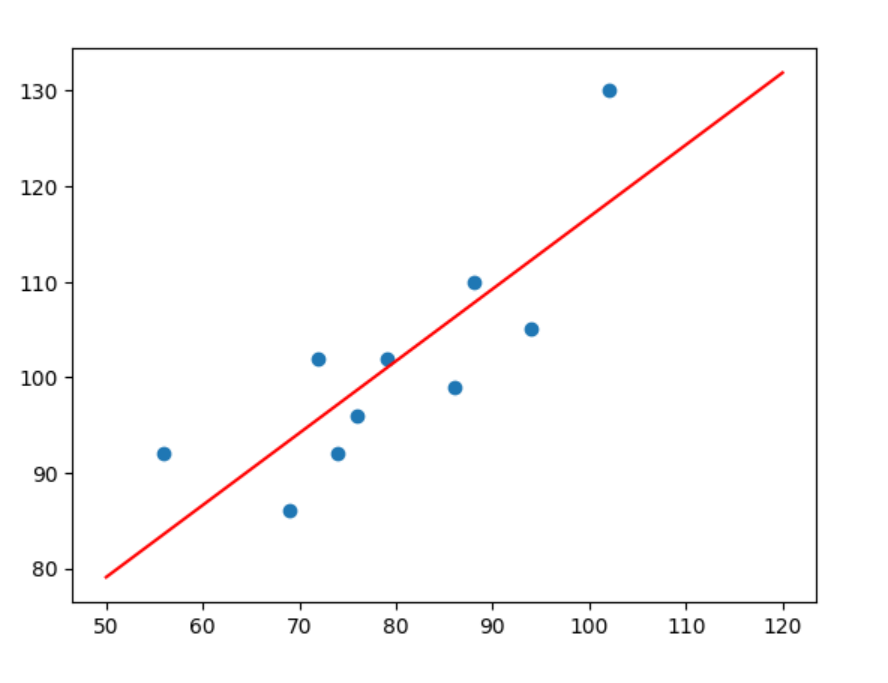
% 检查残差图，确保没有明显的模式
% 残差图应显示随机分布的点 - 无明显模式即表示模型适用 
figure;
scatter(Y,r,'filled');
title('残差图');
xlabel('观测值');
ylabel('残差');

        在代码执行结束后，b 变量包含了估算的回归系数，bint 给出了这些估算系数的95%置信区间，r 包含残差，rint 给出了残差的置信区间，最后输出的stats包含一些关键的统计测度，如R方值、F统计量、p值和误差方差，这些可以用来评估模型的拟合情况。

        具体地，R方值越接近1表示模型的拟合效果越好；F统计量和它的p值用来判断整个回归模型是否显著；每个单独回归系数的p值也可以在输出的bint中找到，如果p值小于0.05(或其他设定的显著性水平)，则认为该系数在统计上是显著的。

        这个MATLAB代码可以直接用于题目中提供的数据，如果要计算其他的数据，只需要把data变量中的值替换为实际数据即可。以上展示的残差图用于诊断模型，理想情况下残差应随机分布，没有明显的模式。如果残差图显示出结构性模式，则表明模型中可能有误差的系统部分未被解释，这表明模型可能需要进一步研究与改进。

得出结果

回归系数 b :
    3.5150
    0.0067
    0.0017
   -0.0043
   -0.0172
    1.4738

系数的95%置信区间 bint:
    0.8519    6.1782
   -0.0071    0.0204
   -0.0163    0.0198
   -0.0174    0.0087
   -0.0559    0.0215
   -1.1954    4.1430

残差 r:
    0.4480
   -0.1949
    0.0709
    0.2667
    0.1163
   -0.4879
   -0.2663
   -0.1985
    0.0260
    0.2237
    0.2302
    0.3195
    0.0593
   -0.1384
   -0.4745

残差的置信区间 rint:
    0.0128    0.8831
   -0.7786    0.3888
   -0.3188    0.4606
   -0.3169    0.8502
   -0.2351    0.4676
   -1.0813    0.1055
   -1.0314    0.4989
   -0.9958    0.5987
   -0.7660    0.8180
   -0.3745    0.8219
   -0.4736    0.9341
   -0.2839    0.9230
   -0.5191    0.6376
   -0.9438    0.6669
   -1.1557    0.2067

统计信息 stats （R方, F统计量, p值,误差方差）:
    0.9097   18.1243    0.0002    0.1256
 

        那么有了这些结果就可以得到我们最终的答案啦~~~