链表基础3——单链表的逆置

news2024/11/15 6:45:34

链表的定义

#include <stdio.h>  
#include <stdlib.h>  
  
typedef struct Node {  
    int data;  
    struct Node* next;  
} Node;  
  
Node* createNode(int data) {  
    Node* newNode = (Node*)malloc(sizeof(Node));  
    if (!newNode) {  
        return NULL;  
    }  
    newNode->data = data;  
    newNode->next = NULL;  
    return newNode;  
}  
  
void printList(Node* head) {  
    Node* current = head;  
    while (current != NULL) {  
        printf("%d ", current->data);  
        current = current->next;  
    }  
    printf("\n");  
}

不带头结点的单向不循环链表的逆置

不带头结点的单向不循环链表的逆置方式主要有以下几种：

  1. 迭代法：
    这种方法使用一个指针遍历链表，同时使用另一个指针指向当前节点的前一个节点。在遍历过程中，每次都将当前节点的next指针指向前一个节点，从而实现链表的逆置。需要注意的是，在逆置过程中，还需要保存下一个要处理的节点，因为逆置后当前节点的next指针会指向前一个节点，从而失去对下一个节点的引用。

  2. 递归法：
    递归法通过递归调用实现链表的逆置。递归的基本思想是：先递归到链表的最后一个节点，然后将该节点的next指针指向它的前一个节点，接着返回前一个节点，继续逆置前面的部分。递归法的好处是代码简洁，但递归深度较大时可能会导致栈溢出。

  3. 栈辅助法：
    这种方法利用栈的后进先出特性来实现链表的逆置。首先将链表中的每个节点依次入栈，然后再依次出栈，并将出栈节点的next指针指向它的前一个出栈节点，从而实现链表的逆置。这种方法需要额外的空间来存储栈中的节点。

  4. 三指针法：
    这种方法使用三个指针，分别指向当前节点、前一个节点和下一个节点。在遍历过程中，先将当前节点的next指针指向前一个节点，然后移动三个指针，继续处理下一个节点。这种方法与迭代法类似，但使用了更多的指针来简化操作。

每种方法都有其特点和适用场景，可以根据具体需求选择合适的方法来实现链表的逆置。在实际应用中，还需要考虑代码的可读性、健壮性和性能等因素。

迭代法

// 迭代法逆置链表  
void reverseListIterative(Node** head) {  
    Node* prev = NULL; // prev指向前一个节点，初始化为NULL  
    Node* current = *head; // current指向当前节点，初始化为头节点  
      
    while (current != NULL) {  
        Node* next = current->next; // next指向下一个节点  
        current->next = prev; // 将当前节点的next指针指向前一个节点，实现逆置  
        prev = current; // 将prev移动到当前节点  
        current = next; // 将current移动到下一个节点  
    }  
      
    *head = prev; // 更新头指针，指向新的头节点（原链表的尾节点）  
}

逐步分解

 

 

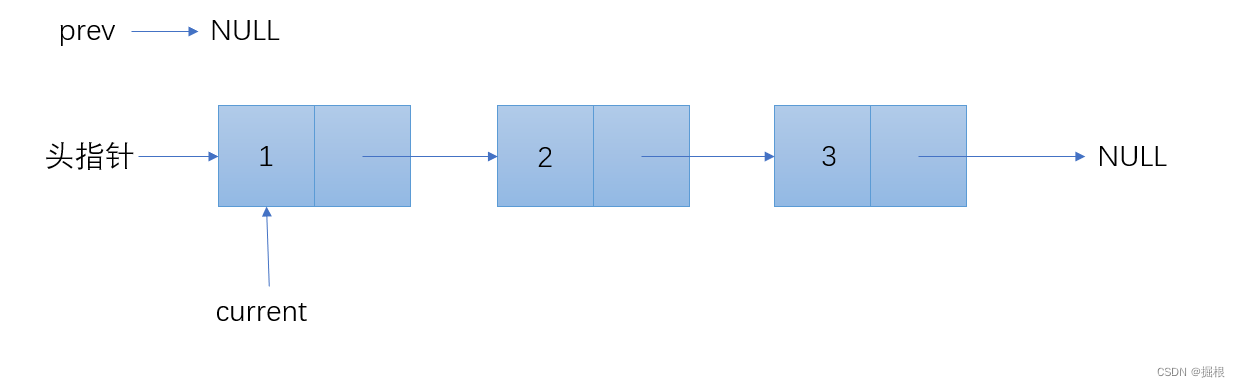
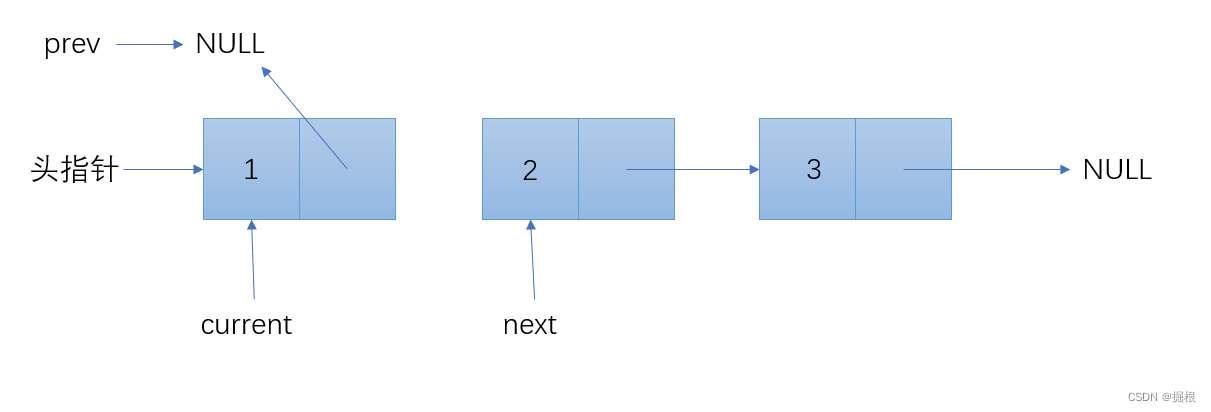
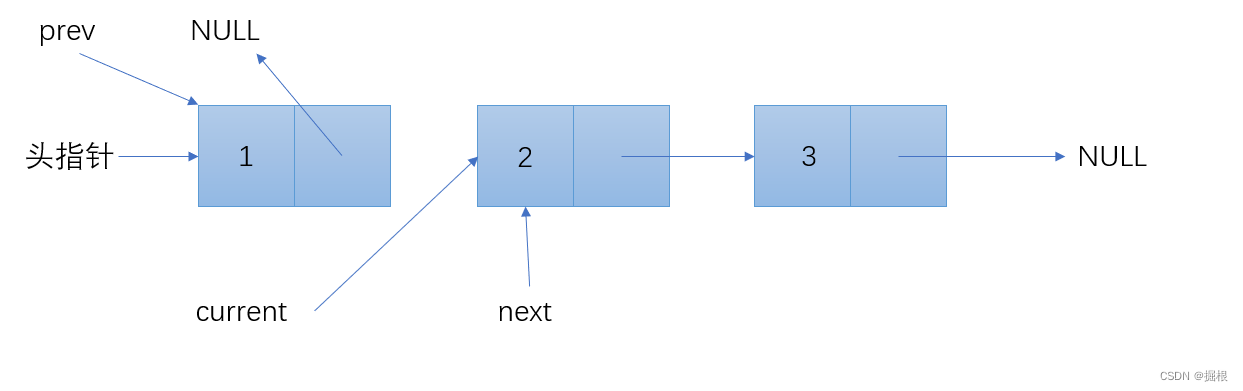
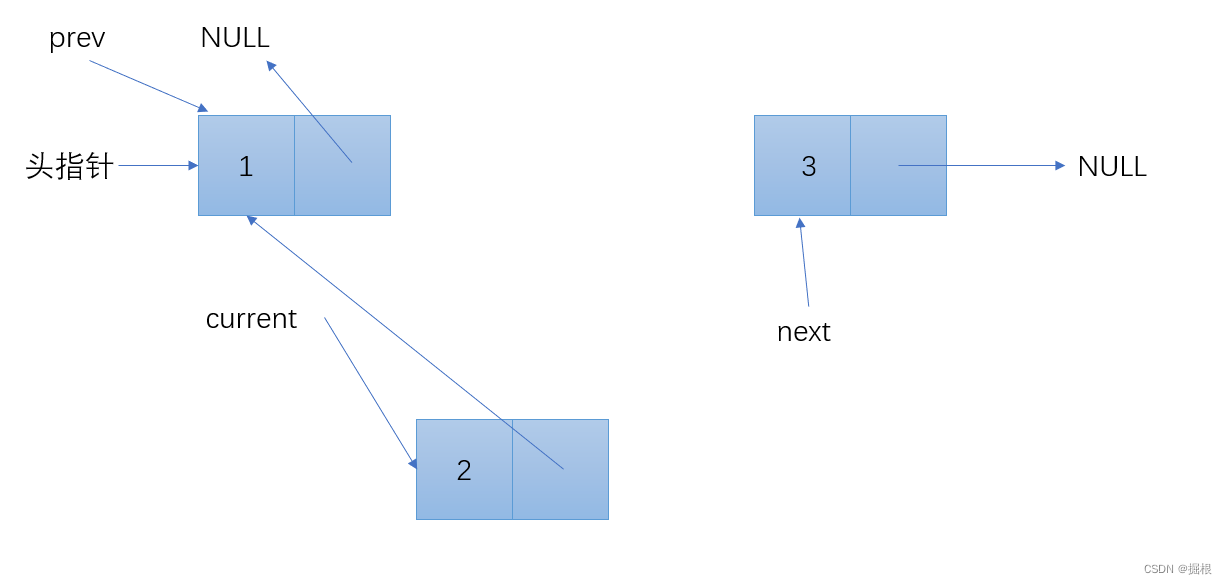
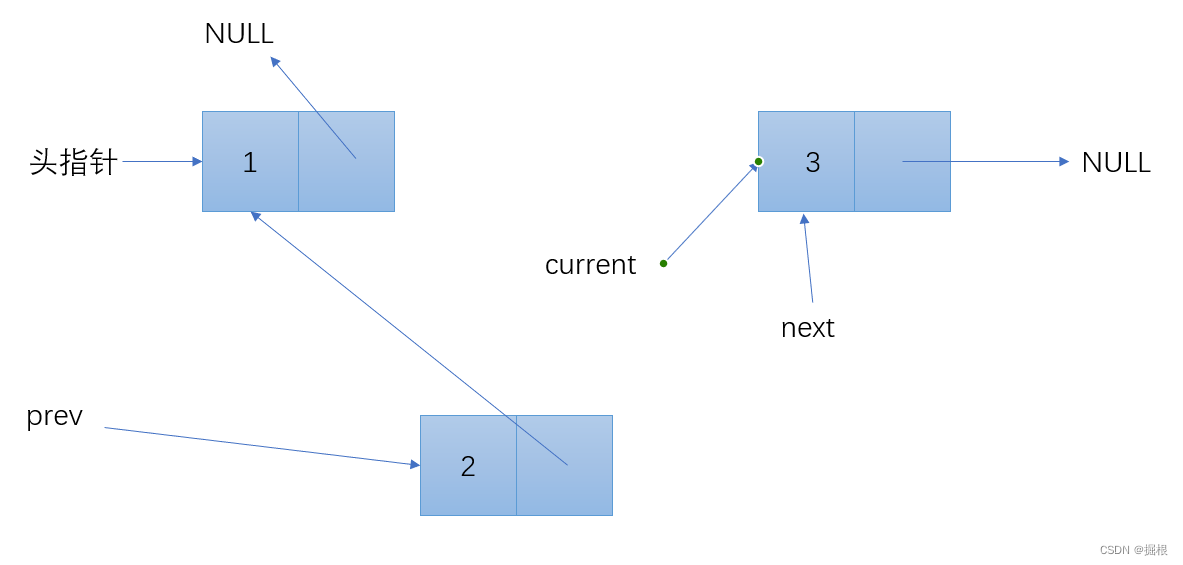
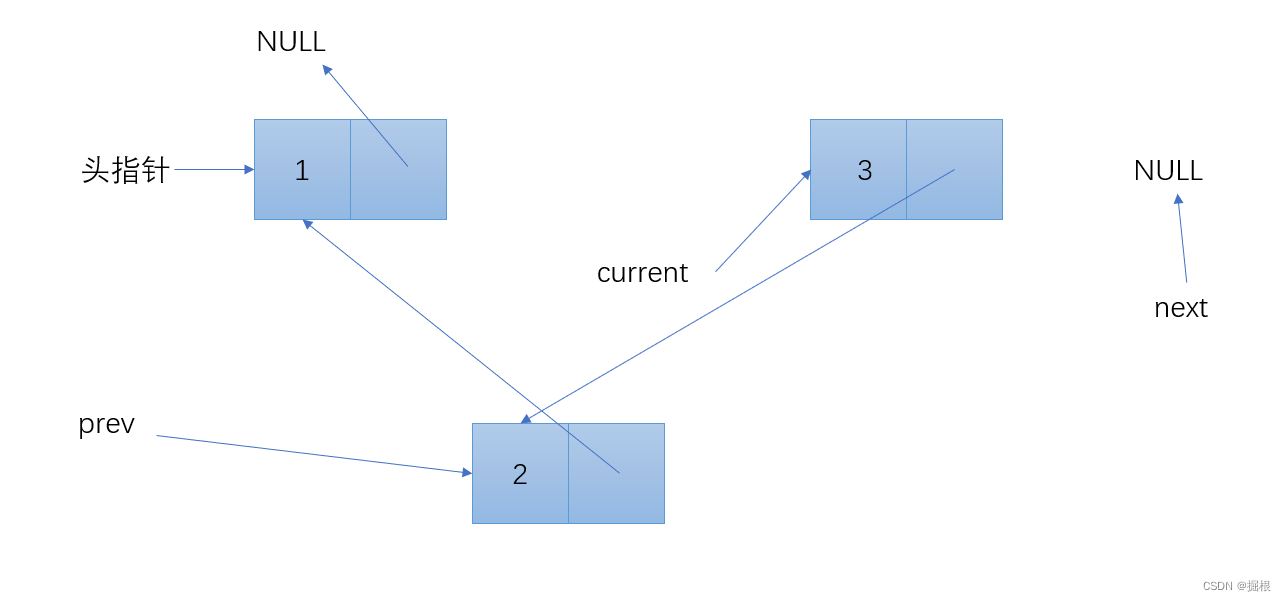
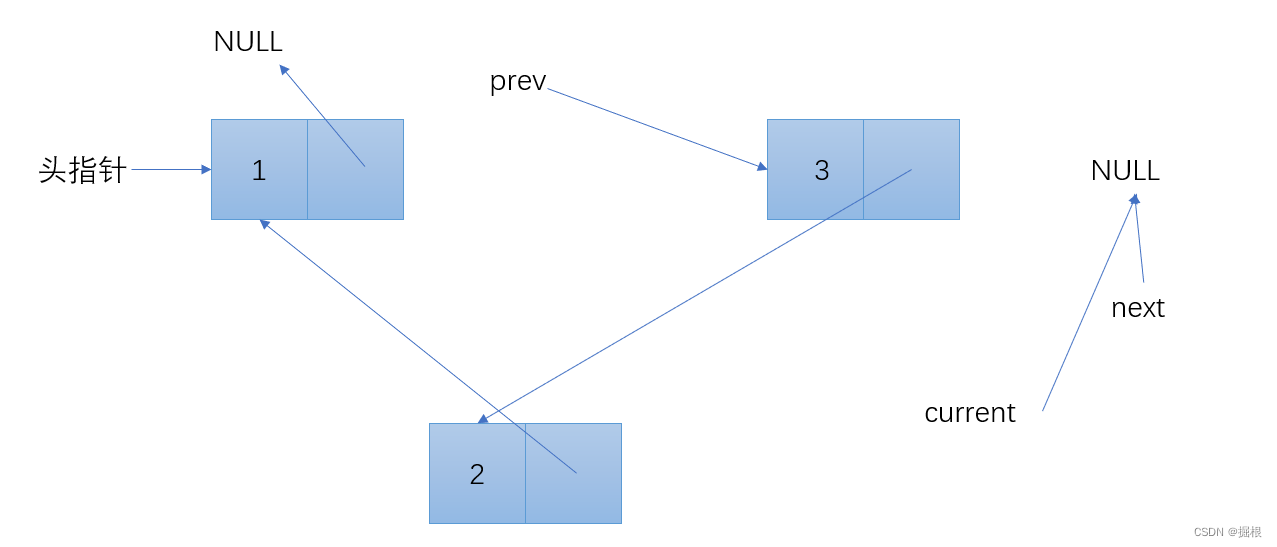
到这里循环就结束了

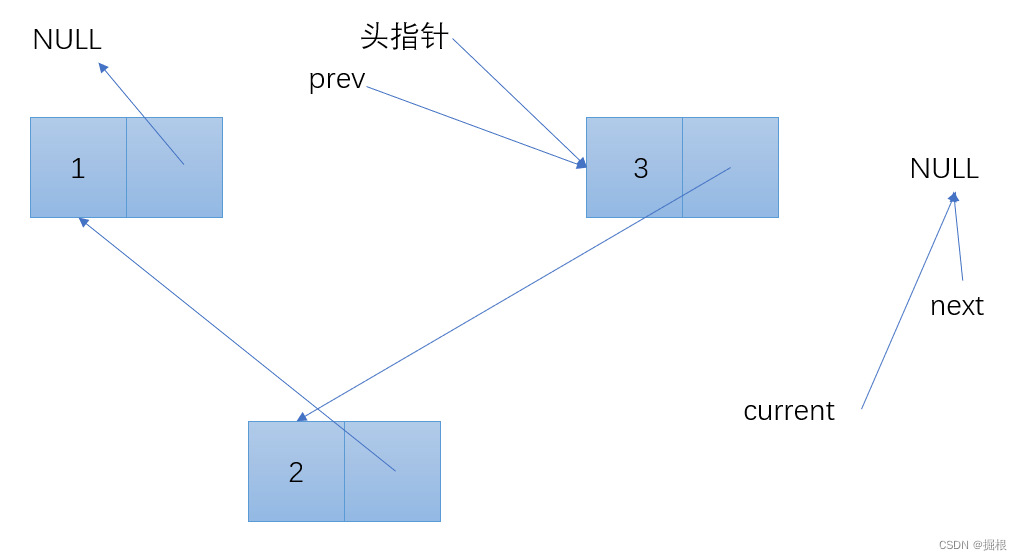 到这里彻底完成链表的逆置 

递归法

// 递归法逆置链表  
Node* reverseListRecursive(Node* head) {  
    // 递归终止条件：当前节点为空或当前节点的下一个节点为空  
    if (head == NULL || head->next == NULL) {  
        return head;  
    }  
      
    // 递归调用，逆置剩余部分链表，并返回新的头节点  
    Node* newHead = reverseListRecursive(head->next);  
      
    // 处理当前节点，将其指向原来的前一个节点，实现逆置  
    head->next->next = head;  
    head->next = NULL;  
      
    // 返回新的头节点  
    return newHead;  
}
  
// main 函数和其他辅助函数与迭代法相同

递归的思想是将一个大问题分解为若干个更小的子问题来解决。在链表逆置的场景中，我们可以将问题分解为“逆置除头节点外的剩余链表，并将头节点放到逆置后链表的尾部”。

递归函数reverseListRecursive的工作过程如下：

  1. 基本情况（递归终止条件）：
    • 如果链表为空（head == NULL），或者链表只有一个节点（head->next == NULL），那么链表已经逆置完成（或者说，无需逆置），直接返回当前头节点。
  2. 递归步骤：
    • 假设当前头节点head的下一个节点开始的链表部分（即剩余链表）已经通过递归调用reverseListRecursive(head->next)逆置完成，并返回了新的头节点newHead。
  3. 处理当前节点：
    • 在递归调用返回后，newHead指向逆置后链表的头节点。此时，我们需要将当前节点head放到逆置后链表的尾部。
    • 由于head->next现在指向逆置后的链表，我们将head->next->next指向head，这样就将head节点添加到了逆置后链表的尾部。
    • 然后，我们需要将head->next设置为NULL，因为head现在是新链表的最后一个节点。
  4. 返回新头节点：
    • 最后，递归函数返回newHead，即逆置后链表的头节点。

这个过程是一个典型的“自底向上”的递归：我们先递归地逆置剩余部分链表，然后再处理当前节点。递归的每一次调用都处理一个更小的子问题，直到到达基本情况（链表为空或只有一个节点）。

以一个简单的例子来说明：

假设链表为 A -> B -> C -> D。

  • 递归调用reverseListRecursive(D)，D没有下一个节点，返回D。
  • 递归调用reverseListRecursive(C)，它首先递归调用reverseListRecursive(D)得到D，然后将C添加到D的前面，得到D -> C，并返回D作为新头节点。
  • 递归调用reverseListRecursive(B)，它首先递归调用reverseListRecursive(C)得到D -> C，然后将B添加到D -> C的前面，得到C -> D -> B，并返回C作为新头节点。
  • 最后，reverseListRecursive(A)调用reverseListRecursive(B)得到C -> D -> B，然后将A添加到C -> D -> B的前面，得到B -> C -> D -> A，并返回B作为新头节点。

最终，A -> B -> C -> D被逆置为B -> C -> D -> A。

通过这种方式，递归能够逐步地将整个链表逆置。希望这个解释能够更清楚地说明递归是如何实现链表逆置的。

栈辅助法

typedef struct Node {  
    int data;  
    struct Node* next;  
} Node;  
  
typedef struct Stack {  
    Node* top;  
} Stack;  
  
void push(Stack* stack, Node* node) {  
    node->next = stack->top;  
    stack->top = node;  
}  
  
Node* pop(Stack* stack) {  
    if (stack->top == NULL) {  
        return NULL;  
    }  
    Node* node = stack->top;  
    stack->top = stack->top->next;  
    node->next = NULL; // 避免悬挂指针  
    return node;  
}  
  
bool isEmpty(Stack* stack) {  
    return stack->top == NULL;  
}  
  
// 栈辅助法逆置链表  
Node* reverseListWithStack(Node* head) {  
    StackNode* stack = createStack();  
    Node* dummy = createNode(0); // 创建一个哑节点作为新链表的头节点  
    Node* tail = dummy; // tail指向新链表的尾节点  
      
    // 将原链表的节点依次入栈  
    while (head != NULL) {  
        push(&stack, head);  
        head = head->next;  
    }  
      
    // 将栈中的节点依次出栈并连接到新链表上  
    while ((head = pop(&stack)) != NULL) {  
        tail->next = head;  
        tail = head;  
    }  
      
    // 新链表的尾节点指向NULL  
    tail->next = NULL;  
      
    // 返回新链表的头节点（哑节点的下一个节点）  
    return dummy->next;  
}  
  
// 辅助函数和main函数与之前相同

三指针法

// 三指针法逆置链表  
Node* reverseListWithThreePointers(Node* head) {  
    if (head == NULL || head->next == NULL) {  
        return head;  
    }  
      
    Node* prev = NULL;  
    Node* current = head;  
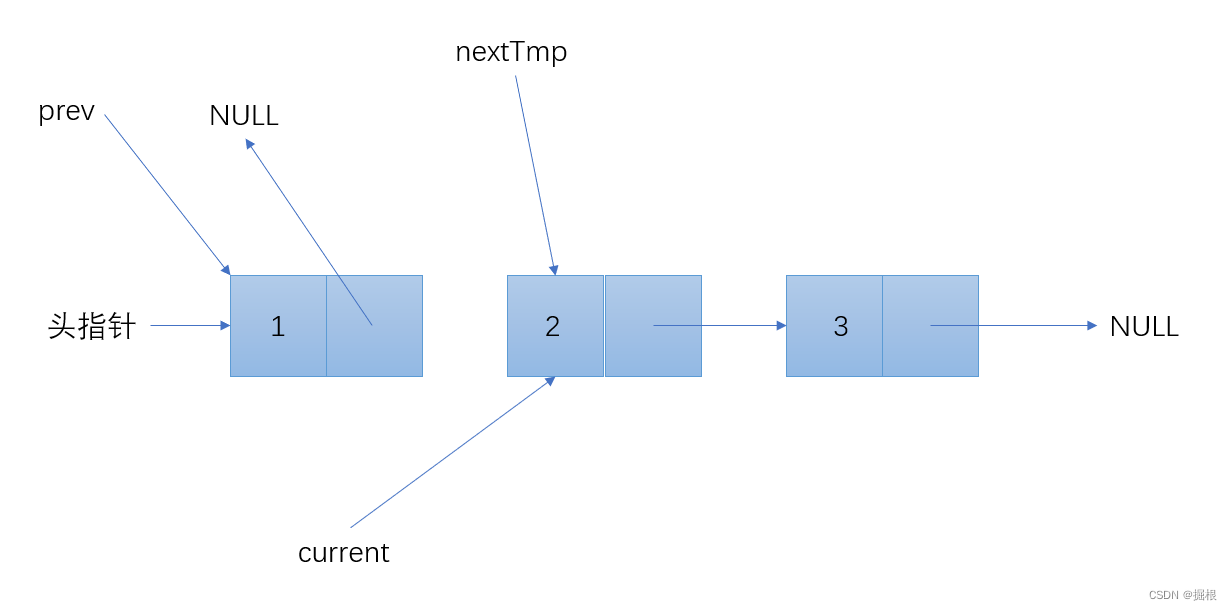
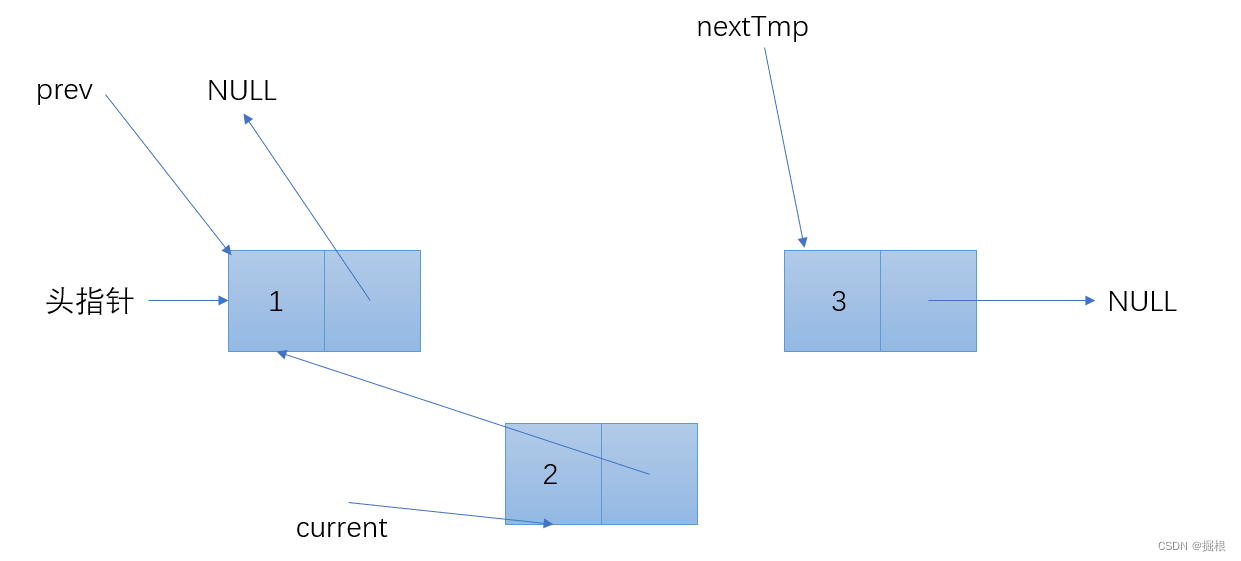
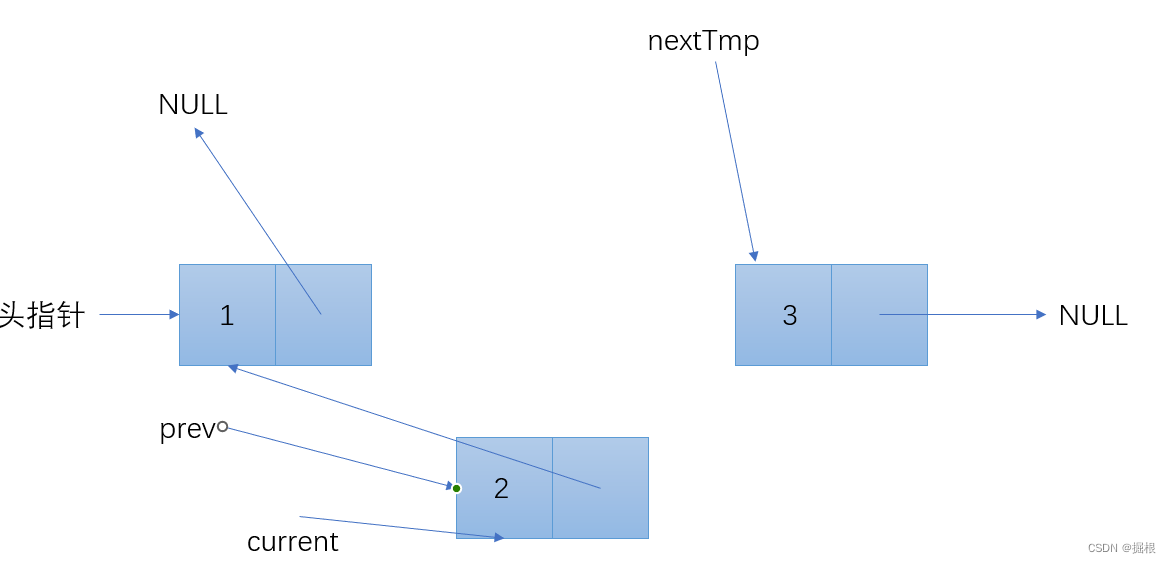
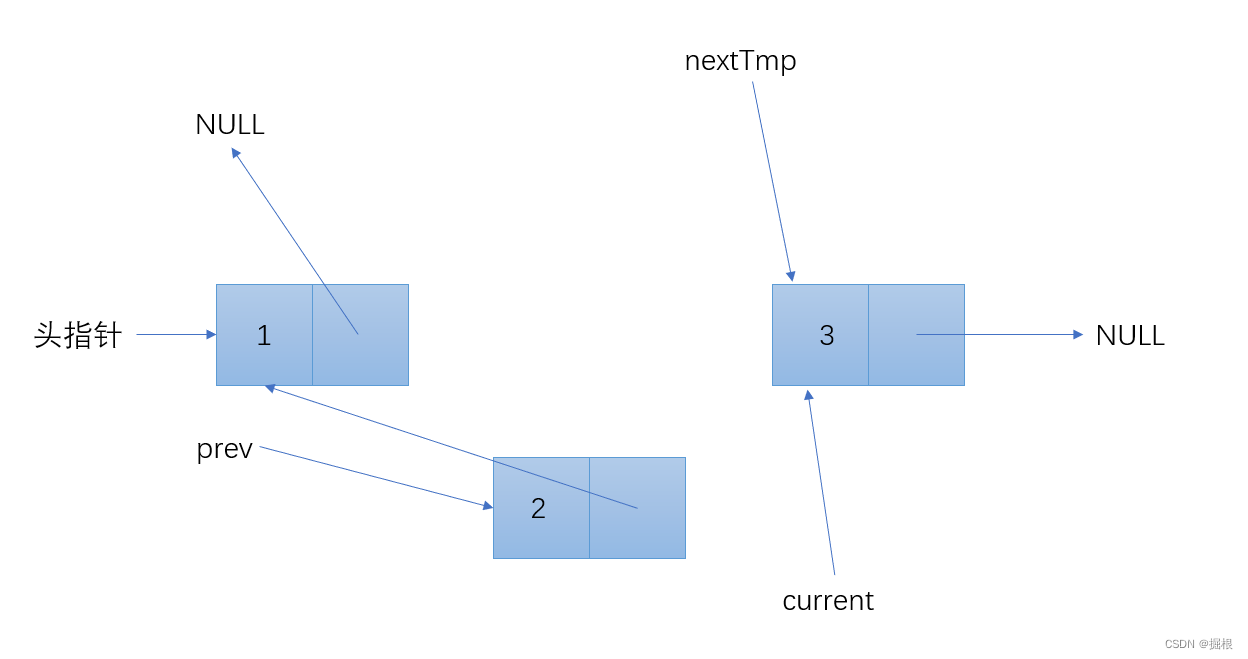
    Node* nextTemp = NULL;  
      
    while (current != NULL) {  
        nextTemp = current->next; // 保存下一个节点  
        current->next = prev; // 反转当前节点的指针  
        prev = current; // prev移动到当前节点  
        current = nextTemp; // current移动到下一个节点  
    }  
      
    return prev; // prev现在指向新的头节点  
}  
  
// ...（其他函数和main函数保持不变）

 逐步分解

 

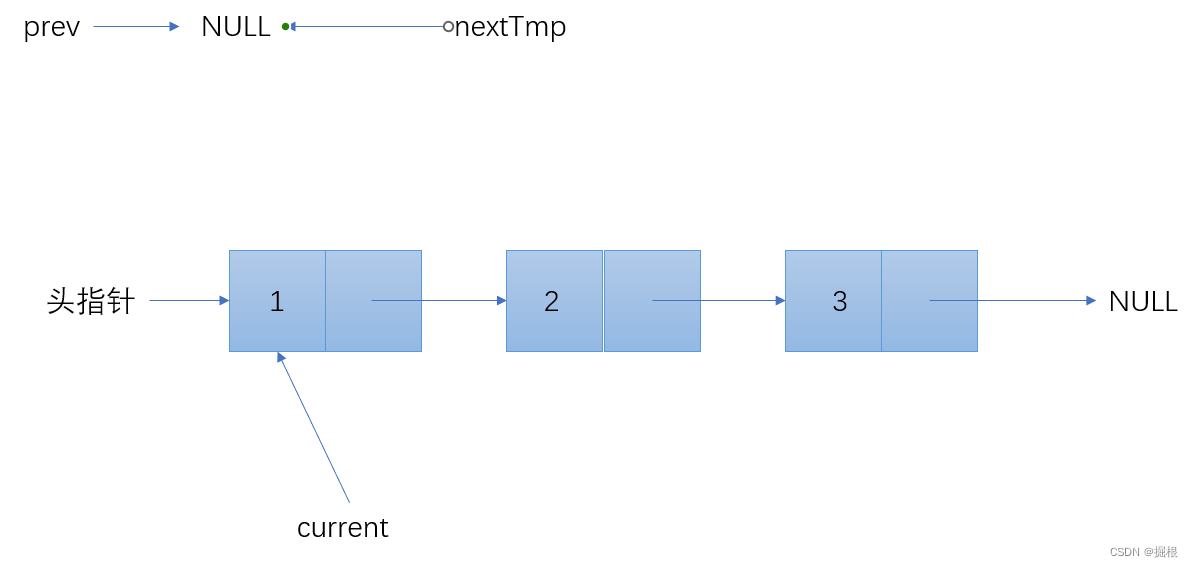
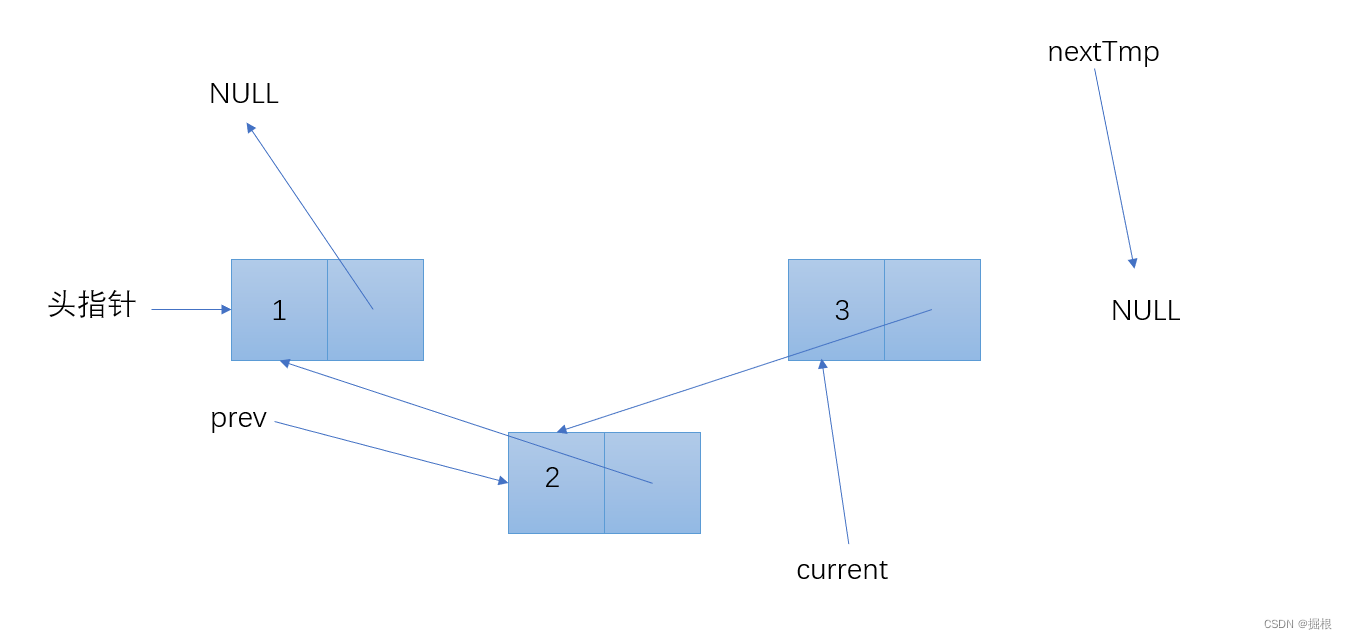
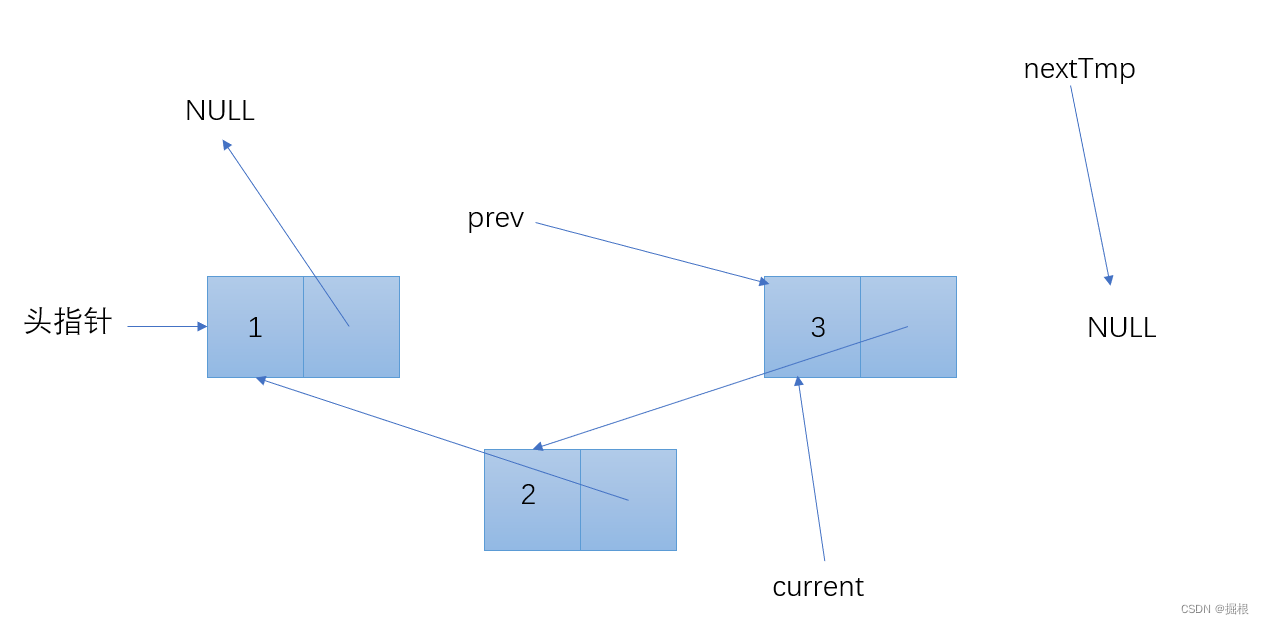
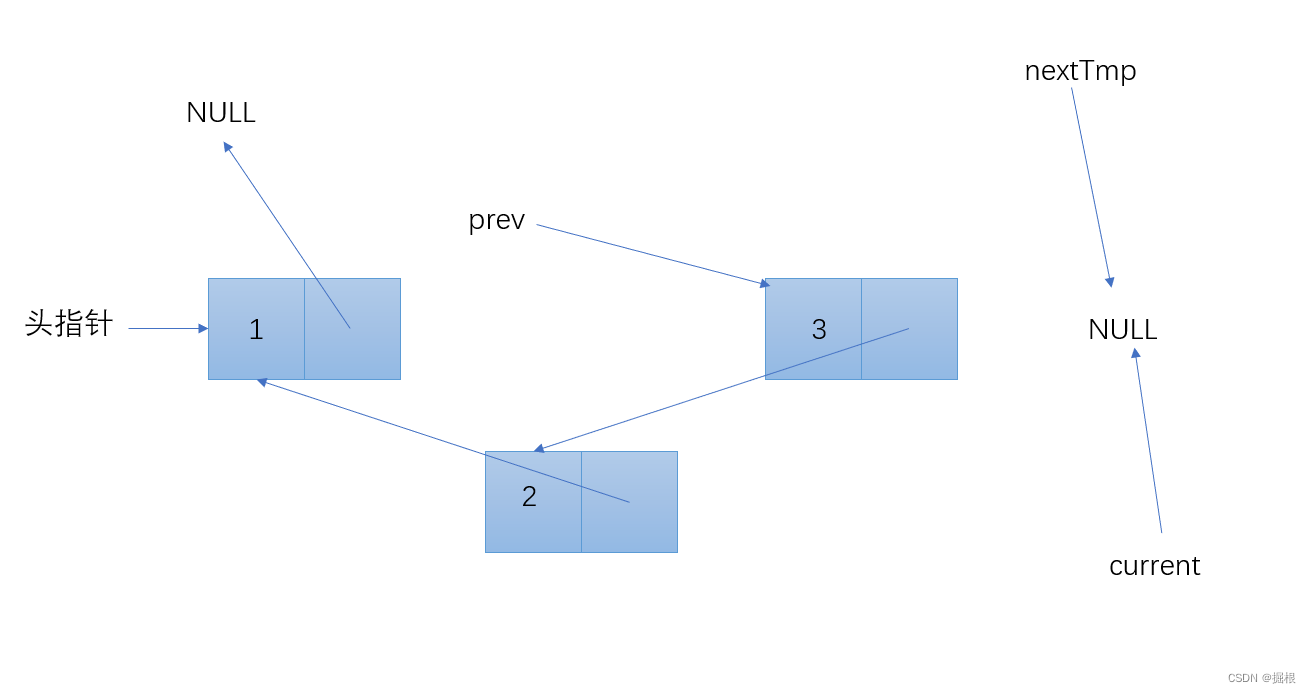
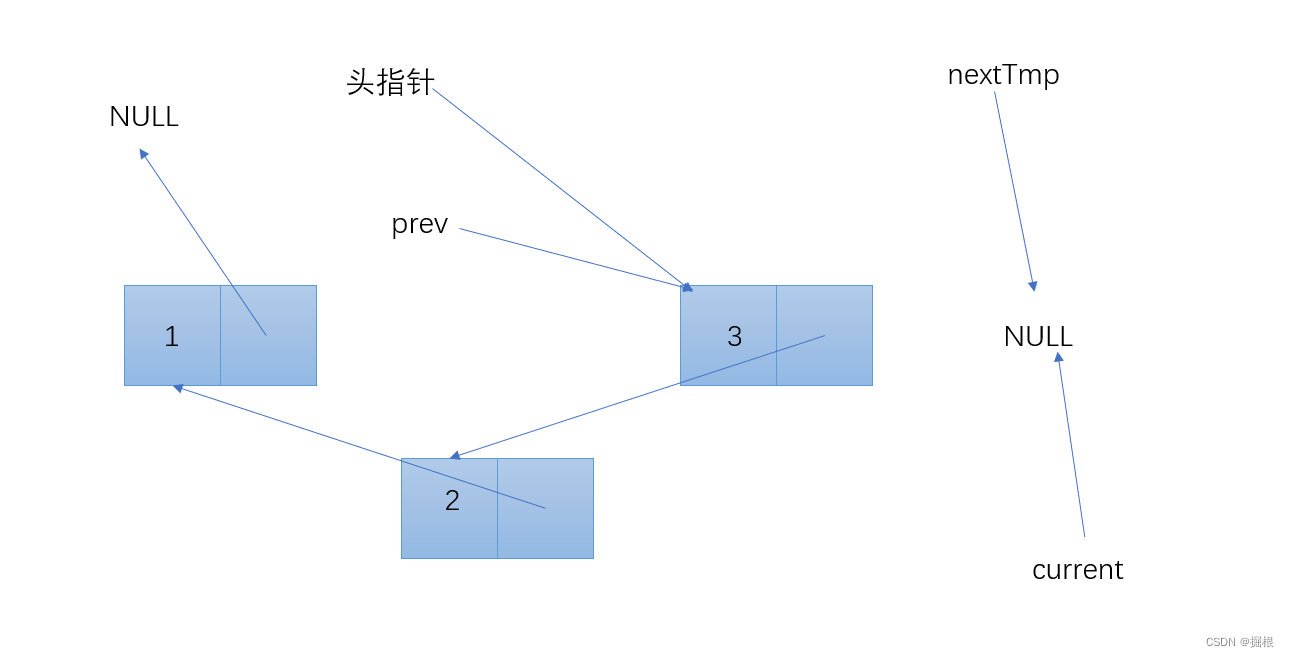
测验代码

int main() {  
    Node* head = createNode(1);  
    head->next = createNode(2);  
    head->next->next = createNode(3);  
    head->next->next->next = createNode(4);  
      
    printf("Original List: ");  
    printList(head);  
      
    reverseListIterative(&head);  
      
    printf("Reversed List: ");  
    printList(head);  
      
    // 释放链表内存  
    Node* temp;  
    while (head != NULL) {  
        temp = head;  
        head = head->next;  
        free(temp);  
    }  
      
    return 0;  
}

带头结点的单向不循环链表的逆置

对于带头结点的单向不循环链表的逆置，我们依然可以使用递归或迭代的方法。

由于头结点通常不存储数据，而是作为链表的起始标识和方便操作，逆置链表时通常不会涉及头结点的变动。

以下，我将分别解释递归和迭代如何对带头结点的单向不循环链表进行逆置。

递归法

在递归法中，我们关注的是链表的当前节点和它的下一个节点。递归的基本思想是：先递归处理子问题（逆置剩余链表），然后处理当前节点。

 typedef struct ListNode {  
 int val;  
 struct ListNode *next;  
 } ListNode;  
   ListNode* reverseListRecursive(ListNode* head) {  
 // 如果链表为空或只有一个节点（即头结点后面没有节点），则无需逆置  
 if (head == NULL || head->next == NULL) {  
 return head;  
 }  
   // 递归调用，逆置头结点后面的链表部分，并返回新的头节点  
 ListNode* newHead = reverseListRecursive(head->next);  
   // 处理当前头结点，将其next指针指向它的前一个节点  
 head->next->next = head;  
   // 将当前头结点的next指针置为NULL，因为它现在是新链表的最后一个节点  
 head->next = NULL;  
   // 返回新的头节点  
 return newHead;  
 } 

在上面的代码中，递归函数reverseListRecursive接收一个指向头结点的指针head，并返回逆置后链表的新的头结点。注意，由于带头结点，我们不会改变头结点的位置，只会改变头结点后面链表的逆置。

迭代法

迭代法则是通过循环和指针操作来逐步逆置链表。对于带头结点的链表，迭代法通常更加直观和易于理解。

 ListNode* reverseListIterative(ListNode* head) {  
 if (head == NULL || head->next == NULL) {  
 return head;  
 }  
   ListNode* prev = head; // prev初始指向头结点  
 ListNode* curr = head->next; // curr初始指向头结点后的第一个节点  
   // 当curr不为空时，持续进行逆置操作  
 while (curr != NULL) {  
 ListNode* nextTemp = curr->next; // 保存curr的下一个节点  
 curr->next = prev; // 将curr的next指针指向前一个节点，实现逆置  
 prev = curr; // prev向后移动一位  
 curr = nextTemp; // curr向后移动一位  
 }  
   // 最后将头结点的next指向新的头节点  
 head->next = prev;  
   // 返回新的头节点  
 return prev;  
 } 

在这个迭代法中，我们使用三个指针：prev始终指向当前逆置部分的最后一个节点，curr指向待逆置的当前节点，nextTemp用于临时存储curr的下一个节点，以便在逆置当前节点后能够继续迭代。

无论是递归还是迭代法，带头结点的单向不循环链表的逆置操作的关键都在于逐步改变节点的next指针的指向，从而实现链表的逆置。

迭代法通常比递归法在空间效率上更优，因为它不需要递归调用栈的空间。而在时间效率上，两者在平均和最坏情况下通常都是O(n)，其中n是链表的长度。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1597156.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

ceph集群管理节点高可用

ceph集群管理节点高可用

一、前言 ceph集群想要高可用也必须要有多个管理节点&#xff0c;不然只有单管理节点&#xff0c;在一个管理节点挂了的情况下就没法进行集群的管理&#xff0c;可以分为web管理和客户端管理&#xff0c;web管理和mgr服务相关&#xff0c;客户端管理和mon服务相关 二、部署 mg…
阅读更多...
品深茶都有什么功效，为什么那么贵？

品深茶都有什么功效，为什么那么贵？

品深国茶是一款高端商务用茶品牌。以中国传统中医理论为指导&#xff0c;精选天然有机茶叶为原料&#xff0c;经过严格配方科学制茶&#xff0c;再经现代生物技术加工制成的高端茶&#xff0c;有排毒养颜、补充营养、调节免疫、调节血脂和血压、调节血糖、促消化、解酒护肝、软…
阅读更多...
【深度学习实战（6）】搭建通用的语义分割推理流程

【深度学习实战（6）】搭建通用的语义分割推理流程

一、代码 #---------------------------------------------------# # 检测图片 #---------------------------------------------------# def detect_image(self, image, countFalse, name_classesNone):#---------------------------------------------------------## 在…
阅读更多...
【题目】【信息安全管理与评估】2022年国赛高职组“信息安全管理与评估”赛项样题6

【题目】【信息安全管理与评估】2022年国赛高职组“信息安全管理与评估”赛项样题6

【题目】【信息安全管理与评估】2022年国赛高职组“信息安全管理与评估”赛项样题5 信息安全管理与评估 网络系统管理 网络搭建与应用 云计算 软件测试 移动应用开发 任务书&#xff0c;赛题&#xff0c;解析等资料&#xff0c;知识点培训服务 添加博主wx&#xff1a;liuliu548…
阅读更多...
Decorator 装饰

Decorator 装饰

意图 动态的给一个对象添加一些额外的职责。就增加功能而言&#xff0c;Decorator模式比生成子类更加灵活 结构 其中&#xff1a; Component定义一个对象接口&#xff0c;可以给这些对象动态的添加职责。ConcreteComponent定义一个对象&#xff0c;可以给这个对象添加一些职…
阅读更多...
C++修炼之路之list模拟实现--C++中的双向循环链表

C++修炼之路之list模拟实现--C++中的双向循环链表

目录 引言 一&#xff1a;STL源代码中关于list的成员变量的介绍 二&#xff1a;模拟实现list 1.基本结构 2.普通迭代器 const迭代器的结合 3.构造拷贝构造析构赋值重载 清空 4.inserterase头尾插入删除 5.打印不同数据类型的数据《使用模板加容器来完成》 三&#xf…
阅读更多...
水库之大坝安全监测系统解决方案

水库之大坝安全监测系统解决方案

一、系统介绍 水库之大坝安全监测系统主要包括渗流监测系统、流量监测系统、雨量监测系统、沉降监测系统组成。每一个监测系统由监测仪器及自动化数据采集装置&#xff08;内置通信装置、防雷设备&#xff09;、附件&#xff08;电缆、通信线路、电源线路&#xff09;等组成&a…
阅读更多...
YOLO算法改进Backbone系列之:HAT-Net

YOLO算法改进Backbone系列之:HAT-Net

本文旨在解决ViT中与多头自我关注&#xff08;MHSA&#xff09;相关的高计算/空间复杂性问题。为此&#xff0c;我们提出了分层多头自注意&#xff08;H-MHSA&#xff09;&#xff0c;这是一种以分层方式计算自注意的新方法。具体来说&#xff0c;我们首先按照通常的方法将输入…
阅读更多...
llama-factory SFT系列教程 (二)，大模型在自定义数据集 lora 训练与部署

llama-factory SFT系列教程 (二)，大模型在自定义数据集 lora 训练与部署

文章目录 简介支持的模型列表2. 添加自定义数据集3. lora 微调4. 大模型 lora 权重&#xff0c;部署问题 参考资料 简介 文章列表&#xff1a; llama-factory SFT系列教程 (一)&#xff0c;大模型 API 部署与使用llama-factory SFT系列教程 (二)&#xff0c;大模型在自定义数…
阅读更多...
ClickHouse--18--argMin() 和argMax()函数

ClickHouse--18--argMin() 和argMax()函数

提示&#xff1a;文章写完后&#xff0c;目录可以自动生成&#xff0c;如何生成可参考右边的帮助文档 文章目录 argMin() 和argMax()函数业务场景使用案例1.准备表和数据&#xff1a;业务场景一&#xff1a;查看salary 最高和最小的user业务场景二&#xff1a;根据更新时间获取…
阅读更多...
一种基于OpenCV的图片倾斜矫正方法

一种基于OpenCV的图片倾斜矫正方法

需求描述&#xff1a; 对倾斜的图片进行矫正&#xff0c;返回倾斜角度和矫正后的图片。 解决方法&#xff1a; 1、各种角度点被投影到一个累加器阵列中&#xff0c;其中倾斜角度可以定义为在最大化对齐的搜索间隔内的投影角度。 2、以不同的角度旋转图像&#xff0c;并为每…
阅读更多...
Chatgpt掘金之旅—有爱AI商业实战篇|编写代码业务|（十九）

Chatgpt掘金之旅—有爱AI商业实战篇|编写代码业务|（十九）

演示站点&#xff1a; https://ai.uaai.cn 对话模块 官方论坛&#xff1a; www.jingyuai.com 京娱AI 一、程序员使用 ChatGPT 进行编码搞副业 程序员不仅拥有将抽象概念转化为实际应用的能力&#xff0c;还通常具备强大的逻辑思维和问题解决能力。然而&#xff0c;许多程序员并…
阅读更多...
宝塔面板安装软件 提示需要[xxxMB]内存 强制不能安装

宝塔面板安装软件 提示需要[xxxMB]内存 强制不能安装

解决方法&#xff1a; 第一步&#xff1a; 编辑修改/www/server/panel/class/下的文件panelPlugin.py vi /www/server/panel/class/panelPlugin.py注释以下判断的内容&#xff1a; ## 第二步&#xff1a; 重启宝塔面板&#xff0c;然后安装即可 bash bt 1
阅读更多...
ROS 2边学边练（25）-- 将多个节点组合到一个进程

ROS 2边学边练（25）-- 将多个节点组合到一个进程

前言 在ROS 2中&#xff0c;将多个节点&#xff08;Nodes&#xff09;组合到一个单独的进程&#xff08;Process&#xff09;中通常指的是使用“Composable Nodes”的特性。这个特性允许你定义可复用的组件&#xff08;Components&#xff09;&#xff0c;然后将这些组件加…
阅读更多...
如何在MobaXterm上使用rz命令

如何在MobaXterm上使用rz命令

1、首先输入命令和想下载的文件&#xff0c;如下图&#xff1a; 2、按住ctrl鼠标右键&#xff0c;选择如下选项&#xff1a; 上传命令是rz&#xff0c;选择Receive...... 下载命令是sz&#xff0c;选择Send...... 3、我这里是要把Linux上的文件下载到我的本地window磁盘&…
阅读更多...
Django之rest_framework（三）

Django之rest_framework（三）

一、GenericAPIView的使用 rest_framework.generics.GenericAPIView 继承自APIVIew，主要增加了操作序列化器和数据库查询的方法，作用是为下面Mixin扩展类的执行提供方法支持。通常在使用时，可搭配一个或多个Mixin扩展类 1.1、属性 serializer_class 指明视图使用的序列化器…
阅读更多...
记录一下买了腾讯云服务器后如何第一次连MobaXterm

记录一下买了腾讯云服务器后如何第一次连MobaXterm

首先是你要用SwitchHost把hosts的映射地址改成你新买的服务器的&#xff08;如果你没这个软件&#xff0c;可以直接在etc/hosts里改 &#xff09; 再连MobaXterm 然后&#xff0c;关键的来了 成功&#xff01;
阅读更多...
2024/4/15 网络编程day3

2024/4/15 网络编程day3

一、TCP机械臂测试 通过w(红色臂角度增大)s&#xff08;红色臂角度减小&#xff09;d&#xff08;蓝色臂角度增大&#xff09;a&#xff08;蓝色臂角度减小&#xff09;按键控制机械臂 注意&#xff1a;关闭计算机的杀毒软件&#xff0c;电脑管家&#xff0c;防火墙 1&#…
阅读更多...
openGauss学习笔记-261 openGauss性能调优-使用Plan Hint进行调优-将部分Error降级为Warning的Hint

openGauss学习笔记-261 openGauss性能调优-使用Plan Hint进行调优-将部分Error降级为Warning的Hint

文章目录 openGauss学习笔记-261 openGauss性能调优-使用Plan Hint进行调优-将部分Error降级为Warning的Hint261.1 功能描述261.2 语法格式261.3 示例261.3.1 忽略非空约束261.3.2 忽略唯一约束261.3.3 忽略分区表无法匹配到合法分区261.3.4 更新/插入值向目标列类型转换失败 o…
阅读更多...
3.MMD快捷键操作及人物绑定配饰

3.MMD快捷键操作及人物绑定配饰

快捷键 1. 模型界面切换 按一下TAB键&#xff0c;就从人物模型切换到照明模型 再按一下TAB键&#xff0c;就能从照明模型切换回人物模型 2. 选中全部模型 当模型界面是人物模型时 而且电脑输入法时英文时 按一下A键&#xff0c;可以把人物骨骼全部选中&#xff0c;方便旋转…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023