线性回归练习 Day1

手搓线性回归

随机初始数据

import numpy as np
x = np.array([56, 72, 69, 88, 102, 86, 76, 79, 94, 74])
y = np.array([92, 102, 86, 110, 130, 99, 96, 102, 105, 92])

from matplotlib import pyplot as plt
# 内嵌显示
%matplotlib inline

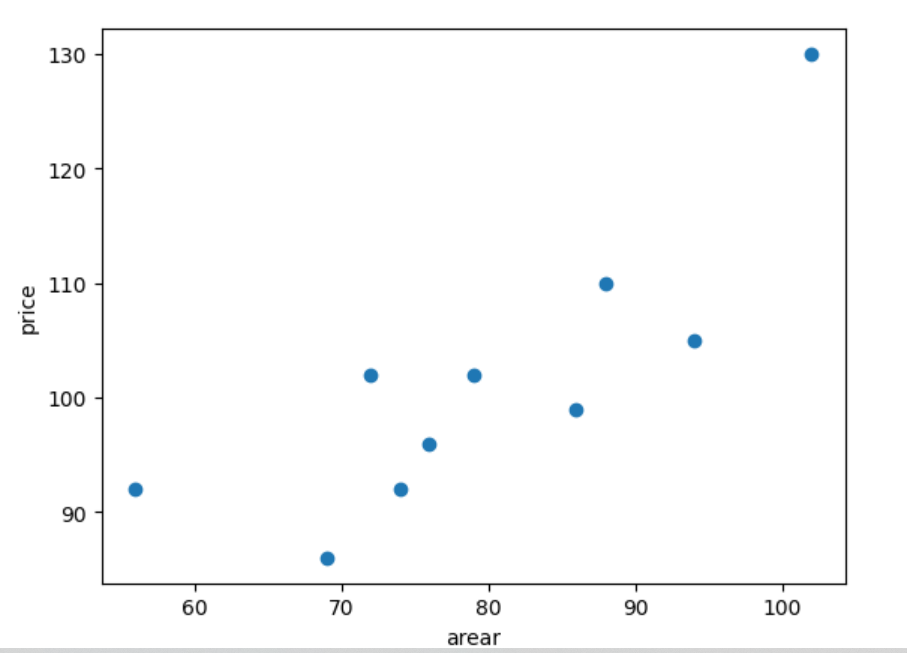
plt.scatter(x, y)
plt.xlabel("arear")
plt.ylabel("price")

Text(0, 0.5, 'price')

​

# 定义线性模型
def f(x ,w0, w1):
    y = w0 +w1*x
    return y

# 定义平方损失函数
def loss(x, y, w0, w1):
    loss = sum(np.square(y-(w0 +w1*x)))
    return loss

最小二乘法 — 定义为：
$$f=\sum _{i=1}^n{(y_i-(w_0+w_1{x}_i))}^2$$
对loss 求w0 和w1 的偏微分，解方程组可得
$$w_1=\frac{n{\sum }_{}^{}{x}_i{y}_i-{\sum }_{}^{}{x}_i{\sum }_{}^{}{y}_i}{n{\sum }_{}^{}{x_i}^2-({\sum }_{}^{}{x}_i{)}^2}$$

$$w_0=\frac{{\sum }_{}^{}{x_i}^2{\sum }_{}^{}{y}_i-{\sum }_{}^{}{x}_i{\sum }_{}^{}{x}_i{y}_i}{n{\sum }_{}^{}{x_i}^2-({\sum }_{}^{}{x}_i{)}^2}$$

# 使用代码实现上述过程 -- 求解最优的w0 和w1
def culculate_w(x, y):
    n = len(x)
    w1 = (n*sum(x*y) - sum(x)*sum(y))/(n*sum(x*x) - sum(x)*sum(x))
    w0 = (sum(x*x)*sum(y) - sum(x)*sum(x*y))/(n*sum(x*x)-sum(x)*sum(x))
    return w0, w1

culculate_w(x, y)

(41.33509168550616, 0.7545842753077117)

w0 = culculate_w(x, y)[0]
w1 = culculate_w(x, y)[1]

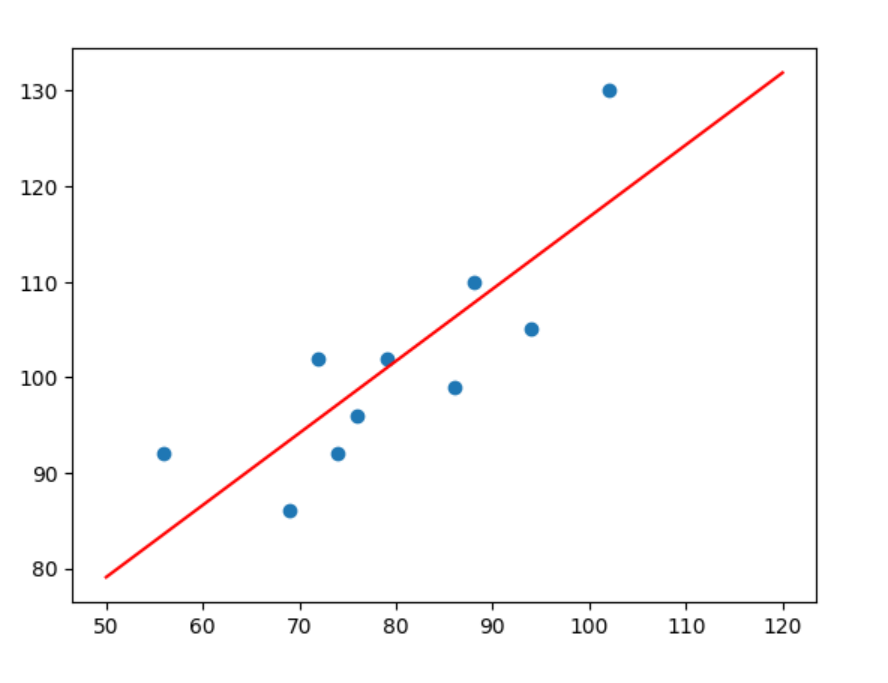
x_temp = np.linspace(50, 120, 100)
plt.scatter(x, y)
%time plt.plot(x_temp, x_temp*w1+w0, "r")

Wall time: 0 ns

​

假设我有一个100平米的房子要售出，则可以表示为：

f(100, w0, w1)

116.79351921627732

使用scikit -learn 实现

sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=1)

• fit_intercept: 默认为 True，计算截距项。
• normalize: 默认为 False，不针对数据进行标准化处理。
• copy_X: 默认为 True，即使用数据的副本进行操作，防止影响原数据。
• n_jobs: 计算时的作业数量。默认为 1，若为 -1 则使用全部 CPU 参与运算。

from sklearn.linear_model import LinearRegression

model = LinearRegression()
 # 训练, reshape 操作把数据处理成 fit 能接受的形状
model.fit(x.reshape(len(x), 1), y)
# 截距项和系数
model.intercept_,model.coef_

(41.33509168550615, array([0.75458428]))

model.predict([[100]])

array([116.79351922])

最小二乘法的矩阵推导（方便运算）

首先，一元线性函数的表达式为 $ y(x, w) = w_0 + w_1x$，表达成矩阵形式为：
$$\left[\begin{array}{c}1,x_1\\ 1,x_2\\ \cdots \\ 1,x_9\\ 1,x_{10}\end{array}\right]\left[\begin{array}{c}{w}_0\\ w_1\end{array}\right]=\left[\begin{array}{c}{y}_1\\ y_2\\ \cdots \\ y_9\\ y_{10}\end{array}\right]\Rightarrow \left[\begin{array}{c}1,56\\ 1,72\\ \cdots \\ 1,94\\ 1,74\end{array}\right]\left[\begin{array}{c}{w}_0\\ w_1\end{array}\right]=\left[\begin{array}{c}92\\ 102\\ \cdots \\ 105\\ 92\end{array}\right]\text{\hspace{1em}(8a)}$$

$$y(x,w)=XW\text{\hspace{1em}(8b)}$$
$(8)$ 式中，$W$ 为 $\left[\begin{array}{c}{w}_0\\ w_1\end{array}\right]$，而 $X$ 则是 $\left[\begin{array}{c}1,x_1\\ 1,x_2\\ \cdots \\ 1,x_9\\ 1,x_{10}\end{array}\right]$ 矩阵。然后，平方损失函数为：
$$f=\sum _{i=1}^n{(y_i-(w_0+w_1{x}_i))}^2=(y-XW{)}^T(y-XW)\text{\hspace{1em}(9)}$$
通过对公式 $(9)$ 实施矩阵计算乘法分配律得到：
在该公式中 $y$ 与 $XW$ 皆为相同形式的 $(m,1)$ 矩阵，由此两者相乘属于线性关系，所以等价转换如下：
$$\begin{gathered} f=y^{T}y-(XW{)}^{T}y-(XW{)}^{T}y+(XW{)}^T(XW) \\ =y^{T}y-2(XW{)}^{T}y+(XW{)}^T(XW)\text{\hspace{1em}(11)} \end{gathered}$$

$$\frac{\partial f}{\partial W}=2X^{T}XW-2X^{T}y=0\text{\hspace{1em}(12)}$$

当矩阵 $X^{T}X$ 满秩时， $(X^{T}X{)}^{-1}{X}^{T}X=E$，且 $EW=W$。所以有 $(X^{T}X{)}^{-1}{X}^{T}XW=(X^{T}X{)}^{-1}{X}^{T}y$，并最终得到：
$$W=(X^{T}X{)}^{-1}{X}^{T}y\text{\hspace{1em}(13)}$$

def w_matrix(x, y):
    w = (x.T *x).I*x.T*y
    return w

# 这里给截距系数加1
# 为什么？
x = np.matrix([[1, 56], [1, 72], [1, 69], [1, 88], [1, 102],
               [1, 86], [1, 76], [1, 79], [1, 94], [1, 74]])
x

matrix([[  1,  56],
        [  1,  72],
        [  1,  69],
        [  1,  88],
        [  1, 102],
        [  1,  86],
        [  1,  76],
        [  1,  79],
        [  1,  94],
        [  1,  74]])

y = np.matrix([92, 102, 86, 110, 130, 99, 96, 102, 105, 92])
y

matrix([[ 92, 102,  86, 110, 130,  99,  96, 102, 105,  92]])

y.reshape(10, 1)

matrix([[ 92],
        [102],
        [ 86],
        [110],
        [130],
        [ 99],
        [ 96],
        [102],
        [105],
        [ 92]])

w_matrix(x, y.reshape(10, 1))  #这里注意一下这个reshape的函数，可以简单介绍一下

matrix([[41.33509169],
        [ 0.75458428]])

实战之波士顿房价

import pandas as pd

df = pd.read_csv(
    "https://labfile.oss.aliyuncs.com/courses/1081/course-5-boston.csv")

df.head()

	crim	zn	indus	chas	nox	rm	age	dis	rad	tax	ptratio	black	lstat	medv
0	0.00632	18.0	2.31	0	0.538	6.575	65.2	4.0900	1	296	15.3	396.90	4.98	24.0
1	0.02731	0.0	7.07	0	0.469	6.421	78.9	4.9671	2	242	17.8	396.90	9.14	21.6
2	0.02729	0.0	7.07	0	0.469	7.185	61.1	4.9671	2	242	17.8	392.83	4.03	34.7
3	0.03237	0.0	2.18	0	0.458	6.998	45.8	6.0622	3	222	18.7	394.63	2.94	33.4
4	0.06905	0.0	2.18	0	0.458	7.147	54.2	6.0622	3	222	18.7	396.90	5.33	36.2

• CRIM: 城镇犯罪率。
• ZN: 占地面积超过 2.5 万平方英尺的住宅用地比例。
• INDUS: 城镇非零售业务地区的比例。
• CHAS: 查尔斯河是否经过 (=1 经过，=0 不经过)。
• NOX: 一氧化氮浓度（每 1000 万份）。
• RM: 住宅平均房间数。
• AGE: 所有者年龄。
• DIS: 与就业中心的距离。
• RAD: 公路可达性指数。
• TAX: 物业税率。
• PTRATIO: 城镇师生比例。
• BLACK: 城镇的黑人指数。
• LSTAT: 人口中地位较低人群的百分数。
• MEDV: 城镇住房价格中位数。

以下是双中括号和单中括号用法的区别：

• df[‘column_name’]：这将返回df中名为’column_name’的列作为一个Series对象。
• df[[‘column_name’]]：即使只选择了一列，这也将返回一个包含单个列的DataFrame对象。
• df[[‘column1’, ‘column2’, …]]：这将返回一个包含多个列的新DataFrame对象。

# 选择特征并进行描述
# 注意这里的特征选择哈，需要用双中括号
features = df[['crim', 'black', 'rm']]
features
这里看出df 是一个矩阵哈

	crim	black	rm
0	0.00632	396.90	6.575
1	0.02731	396.90	6.421
2	0.02729	392.83	7.185
3	0.03237	394.63	6.998
4	0.06905	396.90	7.147
...	...	...	...
501	0.06263	391.99	6.593
502	0.04527	396.90	6.120
503	0.06076	396.90	6.976
504	0.10959	393.45	6.794
505	0.04741	396.90	6.030

506 rows × 3 columns

# 这个函数好啊 df.describe()
features.describe()

	crim	black	rm
count	506.000000	506.000000	506.000000
mean	3.593761	356.674032	6.284634
std	8.596783	91.294864	0.702617
min	0.006320	0.320000	3.561000
25%	0.082045	375.377500	5.885500
50%	0.256510	391.440000	6.208500
75%	3.647423	396.225000	6.623500
max	88.976200	396.900000	8.780000

target = df['medv']  # 目标值数据
pd.concat([features, target], axis = 1).head()

	crim	black	rm	medv
0	0.00632	396.90	6.575	24.0
1	0.02731	396.90	6.421	21.6
2	0.02729	392.83	7.185	34.7
3	0.03237	394.63	6.998	33.4
4	0.06905	396.90	7.147	36.2

• pd.concat()是pandas库中用于合并两个或多个pandas对象的函数。
• axis=1参数指定了合并的方向，axis=1表示沿着水平轴合并，即将target添加为features旁边的新列。

target = df['medv']  # 目标值数据
pd.concat([features, target], axis = 1).head()

split_num = int(len(features)*0.8)  # 得到 70% 位置
# 巧用切片
X_train = features[:split_num]  # 训练集特征
y_train = target[:split_num]  # 训练集目标
X_test = features[split_num:]  # 测试集特征
y_test = target[split_num:]  # 测试集目标

# 建立模型 这里x 和y 都是矩阵哈
model = LinearRegression()
model.fit(X_train, y_train)
model.intercept_, model.coef_

(-32.144190320694356,
 array([-2.56053360e-01, -2.08542666e-03,  9.09551839e+00]))

preds = model.predict(X_test)  # 输入测试集特征进行预测
preds  # 预测结果

array([ 6.84236606,  1.35146498, -0.58345448, 15.11080818, 16.39338694,
       26.10728436,  7.11979357, 24.73385248,  5.07320962,  6.96583067,
       -2.93906591, 21.68892456, 26.72249946,  9.19066152,  3.17485413,
       26.79800917, 22.66348233, 20.01804056, 15.53430933, 21.55521943,
       16.21350586, 17.40588695, 17.75900807, 14.583511  , 22.0962585 ,
       23.36733576, 23.24569317, 27.25939339, 24.44022716, 24.75657544,
       20.54835856, 25.06325907, 22.87213135, 19.90582961, 18.19159772,
       15.80408347, 14.31093718, 22.82690027, 22.14476301, 23.48178335,
       17.3213156 , 26.34194786, 23.25722383, 21.360374  , 20.89514026,
       23.66028342, 27.5207012 , 26.25233117, 23.02385692, 32.20317668,
       26.60052985, 25.88101696, 20.99330272, 19.73972181, 22.61401255,
       20.59648876, 27.04045293, 24.08690317, 22.7804789 , 24.78311323,
       21.49489332, 18.72948302, 20.9798386 , 20.63298594, 16.99866114,
       15.64287713, 22.00664348, 22.65331358, 24.66954478, 29.3713086 ,
       14.41919617, 21.63403039, 24.75754314, 11.52283228, 20.69956041,
       20.04221596, 22.31107232, 26.96924151, 29.78745483, 18.72312515,
       19.8734271 , 23.51562772, 21.18951208, 19.5170519 , 16.60020756,
       16.33450271, 13.46210161, 21.43367535, 21.41808652, 18.8918507 ,
       20.856561  , 18.56139052, 15.97879492, 19.6588178 , 21.71280156,
       17.63786833, 21.78933994, 26.98905942, 22.68108487, 30.46288234,
       28.80218963, 21.86194026])

def mae_value(y_true, y_pred):
    n = len(y_true)
    mae = sum(np.abs(y_true - y_pred))/n
    return mae

def mse_value(y_true, y_pred):
    n = len(y_true)
    mse = sum(np.square(y_true - y_pred))/n
    return mse

mae = mae_value(y_test.values, preds)
mse = mse_value(y_test.values, preds)

print("MAE: ", mae)
print("MSE: ", mse)

MAE:  6.332365508141984
MSE:  59.89375772584887

这主要是因为我们没有针对数据进行预处理。上面的实验中，我们随机选择了 3 个特征，并没有合理利用数据集提供的其他特征。除此之外，也没有针对异常数据进行剔除以及规范化处理。