剩余系，欧拉定理，扩展欧拉定理

news2024/11/20 0:26:12

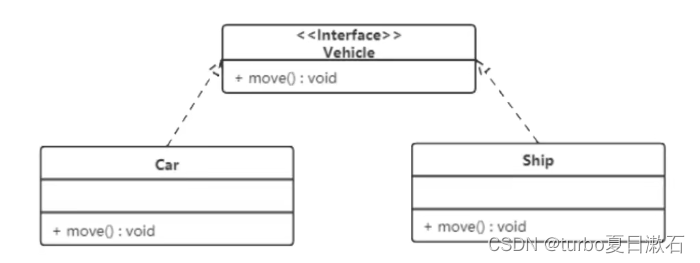
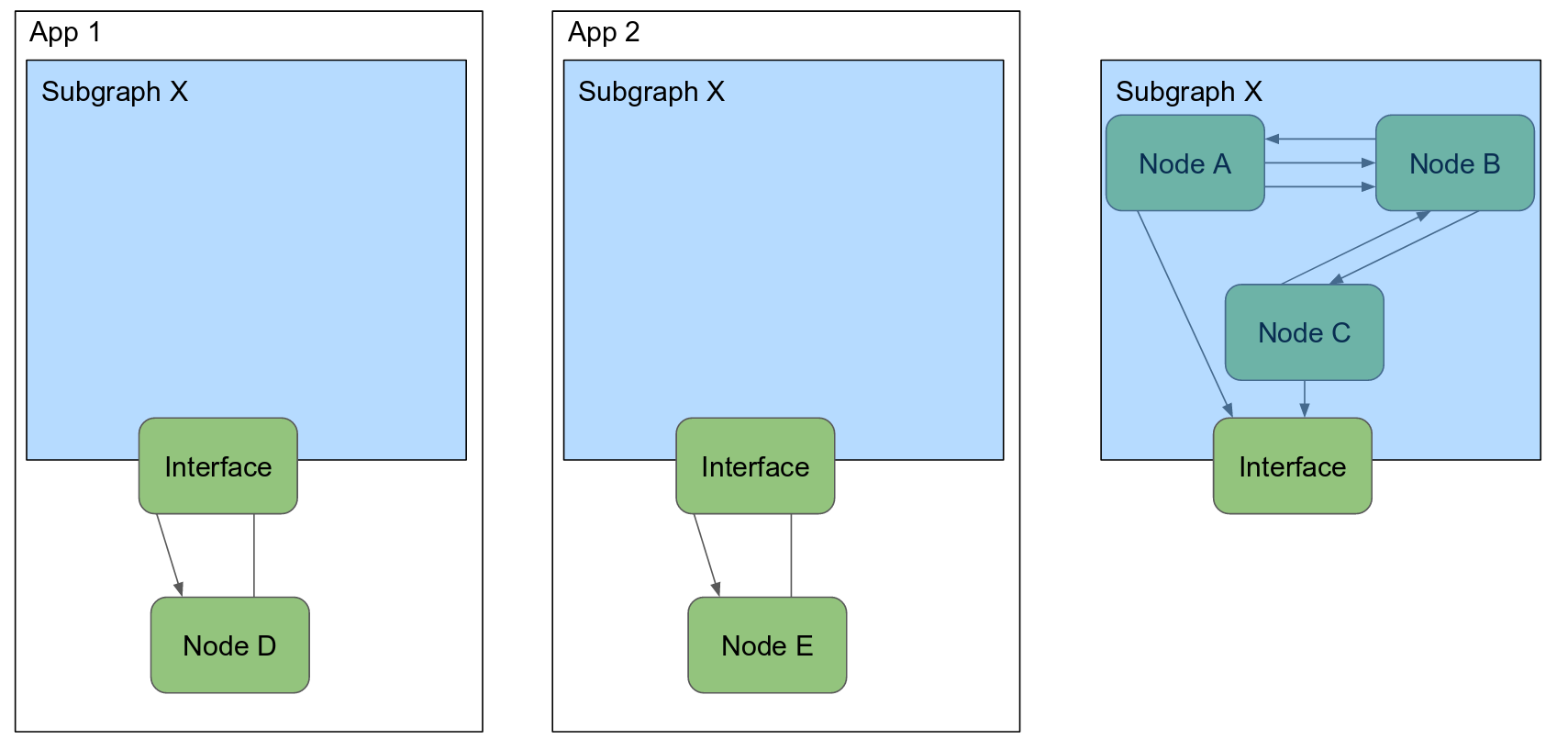
剩余类（同余类）

给定一个正整数n，以 $C_{r}$ r ∈[0, n -1]表示所有形如 $C_{r}=xn+r$ 的整数组成的集合称为模n的剩余类。例n = 5,r = 3,则C3= 5x ＋3为模5的一个剩余类。

完全剩余系（完系）

给定一个正整数n，在模n的剩余类中各取一个元素，则这n个数就构成了模n的一个完全剩余系，总共n个数,将这些数构成一个新的集合，则称这个集合为模n的完全剩余系。

一个数除以4的余数只能是0，1，2，3，{0，1，2，3}和{4，5，-2，11}是模4的完全剩余系。可以看出0和4，1和5，2和-2，3和11模4同余，这4组数分别属于4个剩余类。

简化剩余系（缩系）

给定一个正整数n,有 $\varphi(n)$ 个不同的模n的余数r与n互质的剩余类，从这 $\varphi(n)$ 个剩余类中各取出一个元素，总共 $\varphi(n)$ 个数,将这些数构成一个新的集合，则称这个集合为模n的简化剩余系。

例如，模5的一个简化剩余系是1，2，3，4，模10的一个简化剩余系是1，3，7，9，模18的一个简化剩余系是1，5，7，11，13，17

欧拉函数

在数论，对正整数n，欧拉函数是小于或等于n的正整数中与n互质的数的数目。

$\varphi(n) = n \times\prod_{i=1}^{s}\frac{p_{i}-1}{p_{i}}$

欧拉函数的证明计算可以看我另一篇博客→传送门

好了前置的概念知识介绍完毕，现在引入欧拉定理

欧拉定理

设a,m∈ $N^{+}$ ,且gcd(a,m)=1,则有：

$a^{\varphi(m)}\equiv 1(modm)$

欧拉定理的证明：

设取模m的一个缩系{ $r_{1},r_{2},r_{3},...,r_{\varphi(m)}$ },则{ $ar_{1},ar_{2},ar_{3},...,ar_{\varphi(m)}$ }也是取模m的一个缩系。

所以： $\prod_{i=1}^{\varphi(m)}r_{i}\equiv \prod_{i=1}^{\varphi(m)}ar_{i}\equiv a^{\varphi(m)}\prod_{i=1}^{\varphi(m)}r_{i}(modm)$

根据同余式，约去 $\prod_{i=1}^{\varphi(m)}r_{i}$ ，则可得：

$a^{\varphi(m)}\equiv 1(modm)$

证毕。

另若m为质数，则有 $a^{m-1}\equiv 1(modm)$ ,这正是费马小定理，由此可知费马小定理是欧拉定理的一个特例。

扩展欧拉定理

若 $b<\varphi(m)$ ， $a^{b} \equiv a^{b}(modm)$

若 $b\geqslant \varphi(m)$ ， $a^{b} \equiv a^{b\mod\varphi(m)+\varphi(m)}(modm)$

关于证明可见欧拉定理 & 费马小定理 - OI Wiki (oi-wiki.org)和“欧拉函数详解”附：证明_Cr.rech的博客-CSDN博客

知识学完了，那就上例题→P5091 【模板】扩展欧拉定理 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

根据扩展欧拉定理，根据b的大小我们对其进行降幂操作，欧拉函数可以用筛法或试除法来求，最后跑快速幂即可。

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
char s[20000005];
int MOD;

int qpow(LL a, int b, int m = MOD, int res = 1){
  a %= m;
  while (b > 0) res = (b & 1) ? (res * a % m) : (res), a = a * a % m, b >>= 1;
  return res;
}

int get_phi(int x){
  int ans = x;
  for(int i = 2; i <= x / i; i++){
    if(x % i == 0) {
      ans = ans / i * (i - 1);
      while(x % i == 0) x /= i;
    }
  }
  if(x > 1) ans = ans / x * (x - 1); 
  return ans;
}

int depow(int phi){
  int ans = 0;
  bool flag = 0;
  for(int i = 0; s[i]; i++) {
    ans = ans * 10 + (s[i] - '0');
    if(ans >= phi) flag = 1, ans %= phi; 
  }
  if(flag) ans += phi;
  return ans;
}

int main(){
  int a, m, b;
  scanf("%d%d%s", &a, &MOD, s);
  
  int phi = get_phi(MOD);
  
  b = depow(phi);

  printf("%d", qpow(a, b, MOD));
  return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/159469.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！