快速入门深度学习9.1（用时20min）—

快速入门深度学习9.1（用时20min）——GRU

news2024/10/7 6:46:16

速通《动手学深度学习》9.1

写在最前面
九、现代循环神经网络
- 9.1 门控循环单元（GRU）
- - 9.1.1. 门控隐状态
  - - 9.1.1.1. 重置门和更新门
    - 9.1.1.2. 候选隐状态
    - 9.1.1.3. 隐状态
  - 9.1.3 API简洁实现
  - 小结

请添加图片描述

🌈你好呀！我是是Yu欸 🌌 2024每日百字篆刻时光，感谢你的陪伴与支持 ~ 🚀 欢迎一起踏上探险之旅，挖掘无限可能，共同成长！

写在最前面

很久之前的笔记。草稿箱翻到了。

跳着看的。
最近用到GRU了，所以直接到第九章

学习资料（《动手学深度学习》文档1.0）：http://zh.gluon.ai/chapter_how-to-use/how-to-use.html
（2.0版本）https://zh.d2l.ai/chapter_preface/index.html

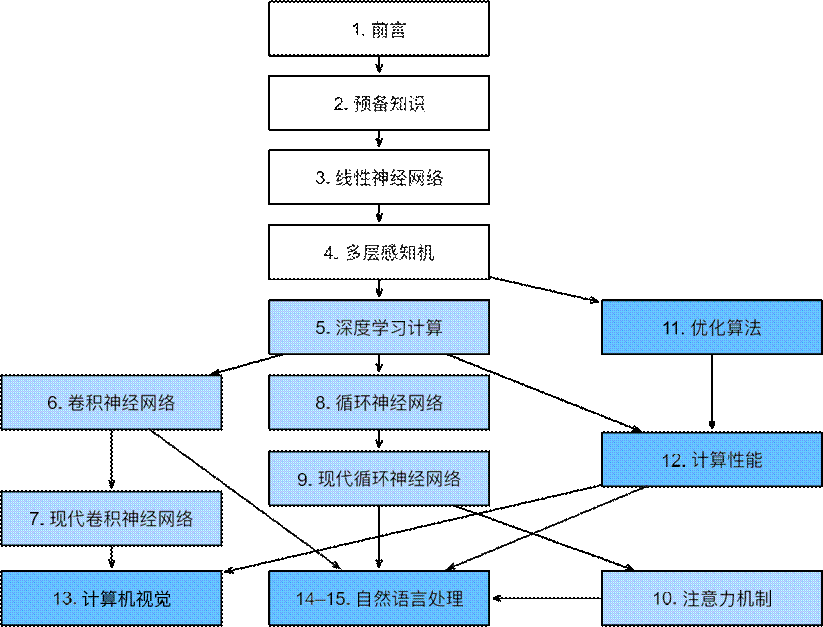
请添加图片描述

第⼀部分包括基础知识和预备知识。
1节提供深度学习的入门课程。
2节中，快速介绍实践深度学习所需的前提条件，例如如何存储和处理数据，以及如何应用基于线性代数、微积分和概率基本概念的各种数值运算。
3节和 4节涵盖了深度学习的最基本概念和技术，例如线性回归、多层感知机和正则化。

第二部分，现代深度学习技术。
5节描述了深度学习计算的各种关键组件，并为我们随后实现更复杂的模型奠定了基础。
6节和 7节中，卷积神经网络（convolutional neural network，CNN），这是构成大多数现代计算机视觉系统骨干的强大工具。
8节和 9节中，循环神经网络(recurrent neural network，RNN)，这是⼀种利用数据中的时间或序列结构的模型，通常用于自然语言处理和时间序列预测。
10节中，注意力机制的技术，最近它们已经开始在自然语言处理中取代循环神经网络。
这一部分将帮助读者快速了解大多数现代深度学习应用背后的基本工具。

第三部分讨论可伸缩性、效率和应用程序。
11节中，用于训练深度学习模型的几种常用优化算法。12节将探讨影响深度学习代码计算性能的几个关键因素。
13节中，展示了深度学习在计算机视觉中的主要应⽤。
14节和 15节中，展示如何预训练语言表示模型并将其应用于自然语言处理任务。

九、现代循环神经网络

9.1 门控循环单元（GRU）

在 8.7节中，讨论了如何在循环神经网络中计算梯度，以及矩阵连续乘积可以导致梯度消失或梯度爆炸的问题。 梯度异常在实践中的意义：

情况1：早期观测值对预测所有未来观测值具有非常重要的意义。
考虑一个极端情况，其中第一个观测值包含一个校验和，目标是在序列的末尾辨别校验和是否正确。在这种情况下，第一个词元的影响至关重要。我们希望有某些机制能够在一个记忆元里存储重要的早期信息。如果没有这样的机制，我们将不得不给这个观测值指定一个非常大的梯度，因为它会影响所有后续的观测值。
情况2：一些词元没有相关的观测值。例如，在对网页内容进行情感分析时，可能有一些辅助HTML代码与网页传达的情绪无关。我们希望有一些机制来跳过隐状态表示中的此类词元。
情况3：序列的各个部分之间存在逻辑中断。例如，书的章节之间可能会有过渡存在，或者证券的熊市和牛市之间可能会有过渡存在。在这种情况下，最好有一种方法来重置内部状态表示。

在学术界已经提出了许多方法来解决这类问题。其中最早的方法是”长短期记忆”（long-short-term memory，LSTM） (Hochreiter and Schmidhuber, 1997)，我们将在 9.2节中讨论。门控循环单元（gated recurrent unit，GRU） (Cho et al., 2014) 是一个稍微简化的变体，通常能够提供同等的效果，并且计算 (Chung et al., 2014)的速度明显更快。由于门控循环单元更简单，我们从它开始解读。

9.1.1. 门控隐状态

门控循环单元与普通的循环神经网络之间的关键区别在于：前者支持隐状态的门控。
这意味着模型有专门的机制来确定应该何时更新隐状态，以及应该何时重置隐状态。这些机制是可学习的，并且能够解决了上面列出的问题。

例如，如果第一个词元非常重要，模型将学会在第一次观测之后不更新隐状态。
同样，模型也可以学会跳过不相关的临时观测。
最后，模型还将学会在需要的时候重置隐状态。
下面将详细讨论各类门控。

9.1.1.1. 重置门和更新门

首先介绍重置门（reset gate）和更新门（update gate）。
我们把它们设计成（0,1）区间中的向量，这样我们就可以进行凸组合。
重置门允许我们控制“可能还想记住”的过去状态的数量；（短期）
更新门将允许我们控制新状态中有多少个是旧状态的副本。（长期）

我们从构造这些门控开始。图9.1.1 描述了门控循环单元中的重置门和更新门的输入， 输入是由当前时间步的输入和前一时间步的隐状态给出。两个门的输出是由使用sigmoid激活函数的两个全连接层给出。

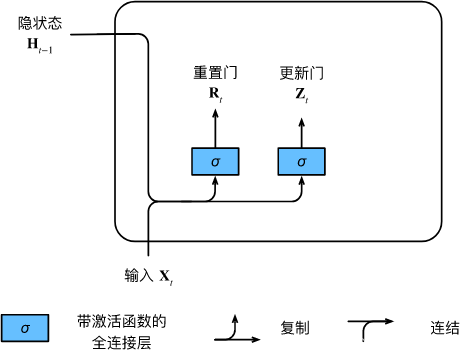
在这里插入图片描述
图9.1.1 在门控循环单元模型中计算重置门和更新门

9.1.1.2. 候选隐状态

在这里插入图片描述
图9.1.2说明了应用重置门之后的计算流程。

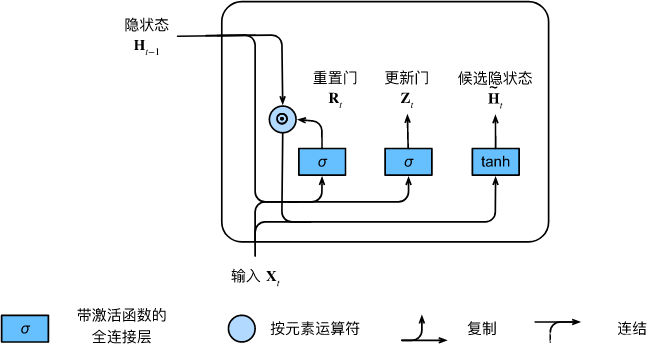
图9.1.2 在门控循环单元模型中计算候选隐状态

9.1.1.3. 隐状态

在这里插入图片描述
这些设计可以帮助我们处理循环神经网络中的梯度消失问题，并更好地捕获时间步距离很长的序列的依赖关系。
例如，如果整个子序列的所有时间步的更新门都接近于1，则无论序列的长度如何，在序列起始时间步的旧隐状态都将很容易保留并传递到序列结束。

图9.1.3说明了更新门起作用后的计算流。
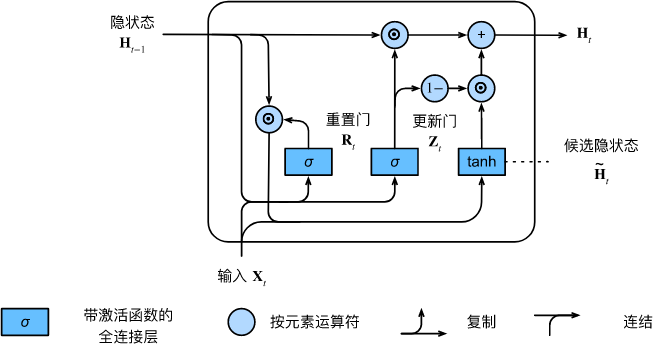
在这里插入图片描述

总之，门控循环单元具有以下两个显著特征：
重置门有助于捕获序列中的短期依赖关系；
更新门有助于捕获序列中的长期依赖关系。

9.1.3 API简洁实现

高级API包含了前文介绍的所有配置细节，所以我们可以直接实例化门控循环单元模型。这段代码的运行速度要快得多，因为它使用的是编译好的运算符而不是Python来处理之前阐述的许多细节。

读取 8.5节中使用的时间机器数据集

import torch
from torch import nn
from d2l import torch as d2l

batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)


num_inputs = vocab_size
gru_layer = nn.GRU(num_inputs, num_hiddens)
model = d2l.RNNModel(gru_layer, len(vocab))
model = model.to(device)
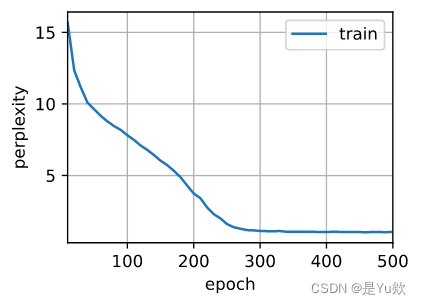
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)

perplexity 1.1, 334788.1 tokens/sec on cuda:0
time traveller with a slight accession ofcheerfulness really thi
travelleryou can show black is white by argument said filby

在这里插入图片描述