一、判断一棵树是否为另一棵树的子树

在编写该函数之前首先应该再编写一个函数判断两个树是否相同，假设两个树分别为t和st，然后再判断若 t和st相同表示st就是t的子树，因为一棵树本身也是自己的子树，否则就判断st是否为t的左子树或是否为t的右子树。

public boolean isEquals(TreeNode root1,TreeNode root2){
        if(root1==null&&root2==null){
            return true;
        }
        if (root1==null||root2==null){
            return false;
        }
        if(root1.val!=root2.val){
            return false;
        }
        return isEquals(root1.left,root2.left)&&isEquals(root1.right,root2.right);
        
    }
    //判断一棵树是否为另一棵树的子树
public boolean isSubtree(TreeNode root, TreeNode subRoot){
        if(root==null||subRoot==null){
            return false;
        }
       if(isEquals(root,subRoot)) return true;
       return isSubtree(root.left,subRoot) || isSubtree(root.right,subRoot);
    }

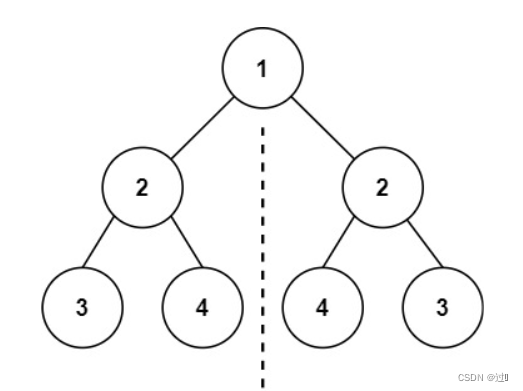
二、判断是否对称二叉树

如上图所示就是二叉树，如果左孩子与右孩子相等，还需要判断左孩子的左孩子的左节点与右孩子的右结点是否相等，然后继续递归判断。

public boolean isSymmetric(TreeNode root) {
       if(root==null){
           return false;
       }
       return isSymmetricChild(root.left,root.right);
    }
public boolean isSymmetricChild(TreeNode lc,TreeNode rc) {
       if(lc==null&&rc==null){
           return true;
       }
       if(lc==null||rc==null){
           return false;
       }
       if(lc.val!=rc.val){
           return false;
       }
       return isSymmetricChild(lc.left,rc.right) && isSymmetricChild(lc.right,rc.left);
    }

三、翻转二叉树

若二叉树不为空，就将二叉树的左右结点进行交换，接着递归交换左子树，最后递归交换右子树。

public TreeNode invertTree(TreeNode root) {
        if(root==null){
            return null;
        }
        TreeNode temp=root.left;
        root.left=root.right;
        root.right=temp;
        invertTree(root.left);
        invertTree(root.right);
        return root;
    }

四、二叉树构建及遍历

题目描述：编一个程序，读入用户输入的一串先序遍历字符串，根据此字符串建立一个二叉树（以指针方式存储）。例如如下的先序遍历字符串： ABC##DE#G##F### 其中“#”表示的是空格，空格字符代表空树。建立起此二叉树以后，再对二叉树进行中序遍历，输出遍历结果。

解题思路：对字符串进行遍历，若遍历得到的字符不为‘#’则表示非空，就将该字符包装为二叉树的根结点，然后继续递归遍历分别用该根结点的左右孩子结点接收。

static class TreeNode{
        char val;
        TreeNode left;
        TreeNode right;
        public TreeNode(char val){
            this.val=val;
        }
    }
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        // 注意 hasNext 和 hasNextLine 的区别
        while (in.hasNextLine()) { // 注意 while 处理多个 case
            String str=in.nextLine();
            TreeNode root=createTree(str);
            inOrder(root);
        }
    }
    public static int i = 0;
    public static TreeNode createTree(String str) {
        TreeNode root = null;
        if(str.charAt(i) != '#') {
            root = new TreeNode(str.charAt(i));
            i++;
            root.left = createTree(str);
            root.right = createTree(str);
        }else {
            i++;
        }
        return root;
    }
    public static void inOrder(TreeNode root){
        if(root==null){
            return;
        }
        inOrder(root.left);
        System.out.print(root.val+" ");
        inOrder(root.right);
    }

五、根据二叉树创建字符串

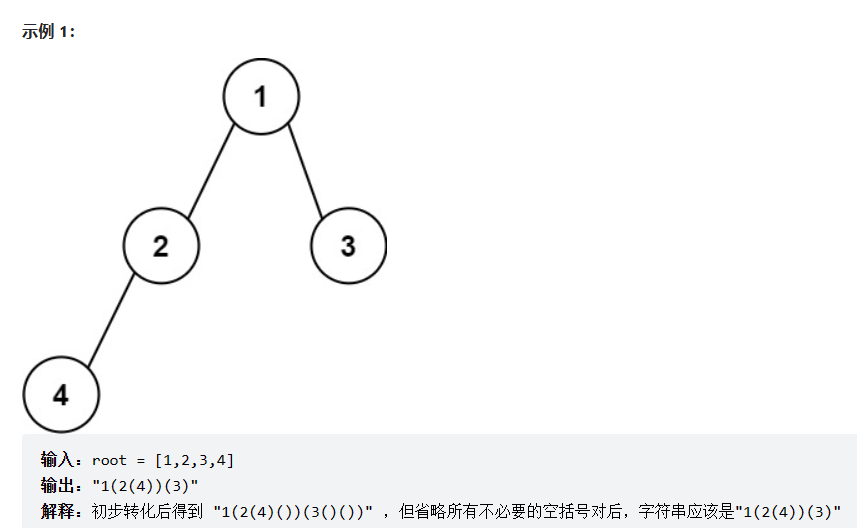
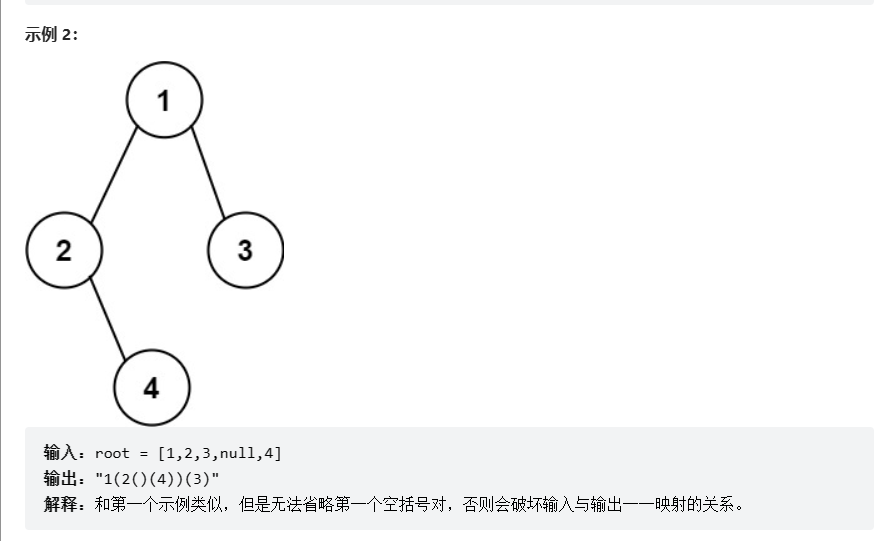
题目描述：给你二叉树的根节点 root ，请你采用前序遍历的方式，将二叉树转化为一个由括号和整数组成的字符串，返回构造出的字符串。空节点使用一对空括号对 "()" 表示，转化后需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。

解题思路：由示例1和示例2可以推出当一个结点的左孩子为空右孩子不为空时就需要添加“（）”,如果左孩子不为空，右孩子为空时直接忽略，左右孩子都为空也是直接忽略。

对树进行遍历，若左子树不为空则需要添加“（”，对左子树进行递归遍历，结束后加上“）”，若左子树为空，右子树不为空就要添加“（）”,否则直接返回，接着继续对右子树遍历，若右子树不为空，则添加“（”，对右子树进行递归遍历，结束后加上“）”。

public String tree2str(TreeNode root) {
        if(root==null){
            return null;
        }
        StringBuilder stringBuilder=new StringBuilder();
        treeStr(root,stringBuilder);
        return stringBuilder.toString();

    }
    public void treeStr(TreeNode root,StringBuilder stringBuilder){
        if(root == null){
            return;
        }
        stringBuilder.append(root.val);
        if(root.left!=null){
            stringBuilder.append("(");
            treeStr(root.left,stringBuilder);
            stringBuilder.append(")");
        }else{
            if(root.right!=null){
                stringBuilder.append("()");
            }else{
                return;
            } }
        if(root.right!=null){
            stringBuilder.append("(");
            treeStr(root.right,stringBuilder);
            stringBuilder.append(")");
        }else {
            return;
        }
    }

六、二叉树的最近公共祖先

最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先），已知p、q全都存在于这棵二叉树。

解题思路一：

使用递归的思想，在树不为空的情况下，若根结点为p或q就直接返回根结点，然后递归遍历左子树和右子树分别用node1和node2接收，如果node1和node2都不为空，则表示这两个结点分别在根结点的两侧，那么就返回根结点，若有node1不为空或node2不为空就返回node1和node2，若都为空则就返回null。

public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root==null){
            return null;
        }
        if(p==root||q==root){
            return root;
        }
        TreeNode node1=lowestCommonAncestor(root.left,p,q);
        TreeNode node2=lowestCommonAncestor(root.right,p,q);
       if(node1 != null && node2 != null){
           return root;
       }else if(node1 != null){
           return node1;
       }else if(node2 != null){
           return node2;
       }else{
           return null;
       }
    }

解题思路二：

可以通过求两个结点从根结点到其的路径，然后通过遍历路径来求最近公共祖先，那么如何求路径？

求路径使用栈结构利用其先进后出的思想，如果所遍历的结点不是路径就可以将其弹出，首先如果根结点和要求路径的结点都不为空，首先将根结点入栈，如果根结点就是要求路径的结点就直接返回true，否则就求路径递归左子树，如果递归结果为真则表示已经找到就返回true，否则就求路径递归右子树，如果递归结果为真也返回true，否则就表示左右子树都未找到就需要弹出结点，然后返回false。

在求最近公共祖先的方法中分别对p和q调用求路径的方法，然后将路径存放到各自的栈，对两个栈进行遍历，查看是否有最近公共祖先。

public TreeNode lowestCommonAncestor2(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null || p == null || q == null){
            return null;
        }
        Deque<TreeNode> stack1=new LinkedList<>();
        Deque<TreeNode> stack2=new LinkedList<>();
        getPath(root,p,stack1);
        getPath(root,q,stack2);
        int size =stack1.size()-stack2.size();
        if(size>0){
            while(size != 0){
                stack1.pop();
                size--;
            }
        }else{
            size=stack2.size()-stack1.size();
            while(size != 0){
                stack2.pop();
                size--;
            }
        }
        while(!stack1.isEmpty() && !stack2.isEmpty()){
            TreeNode node1 = stack1.pop();
            TreeNode node2 = stack2.pop();
            if(node1 == node2){
                return node1;
            }
        }
        return null;
    }
   public boolean getPath(TreeNode root, TreeNode node, Deque<TreeNode> stack){
        if(root == null || node == null){
            return false;
        }
        stack.push(root);
        if(root == node){
            return true;
        }
        boolean flag1 = getPath(root.left,node,stack);
        if(flag1){
            return true;
        }
       boolean flag2 = getPath(root.right,node,stack);
       if(flag2){
           return true;
       }
       stack.pop();
       return false;
    }

七、根据前序遍历和中序遍历构造二叉树

前序遍历的顺序是根-左-右，中序遍历的顺序是左-根-右，就可以创建一个递归函数，参数为前序遍历数组和中序遍历的数组以及开始点ib和结束点ie，当ib>ie是就退出递归，此时已经越界，否则就将i所指的元素包装为根结点，可以定义一个变量i从0开始对前序遍历的序列进行遍历，得到i对应的元素k，k就为根结点，然后在中序遍历中查找k对应的下标index，那么左子树的范围就是0~index-1，右子树的范围是index+1~len，len表示数组长度，然后逐步递归，最后返回root。

public static int i=0;
    public static TreeNode buildTree(int[] preorder, int[] inorder) {
        return buildTreeChild(preorder,inorder,0,inorder.length-1);
    }
    public static TreeNode buildTreeChild(int[] preorder, int[] inorder,int ib,int ie) {
        if(ib>ie){
            return null;
        }
        TreeNode root=new TreeNode(preorder[i]);

        int index=find(inorder,root.val,ib,ie);

        i++;
        root.left=buildTreeChild(preorder,inorder,ib,index-1);

        root.right=buildTreeChild(preorder,inorder,index+1,ie);
        return root;

    }
    public static int find(int[] arr,int num,int begin,int end){
        for (int i=begin;i<=end;i++){
            if(arr[i] == num){
                return i;
            }
        }
        return -1;
    }

八、根据后序遍历和中序遍历构造二叉树

与上题类似，但是后序遍历的顺序是左-右-根，后序遍历的最后一个元素为根节点，那么定义的i变量就从后往前进行遍历，同时需要先创建右子树再创建左子树。

public  static int k=0;
public static TreeNode buildTree2(int[] inorder, int[] postorder) {
        k=postorder.length-1;
        return buildTreeChild2(postorder,inorder,0,inorder.length-1);
    }
public static TreeNode buildTreeChild2(int[] postorder, int[] inorder,int ib,int ie) {
        if(ib>ie){
            return null;
        }
        TreeNode root=new TreeNode(postorder[i]);
        int index=find(inorder,root.val,ib,ie);
        k--;
        root.right=buildTreeChild2(postorder,inorder,index+1,ie);
        root.left=buildTreeChild2(postorder,inorder,ib,index-1);

        return root;
    }
public static int find(int[] arr,int num,int begin,int end){
        for (int i=begin;i<=end;i++){
            if(arr[i] == num){
                return i;
            }
        }
        return -1;
    }

九、二叉树前序非递归遍历

前序遍历的顺序是根-左-右，遍历结果使用list接收，那么就可以使用栈，在树非空的情况下，就定义一个结点cur指向根结点，然后一直向下指向该结点的左子树并将cur添加到list中，list每次接收的都是子树的根结点如果cur为空了，就弹出栈顶元素top，此时栈顶元素刚好存放的是cur的根结点，就让cur指向top，如果此时栈也不为空并且cur也不为空，就继续循环。

public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> list = new LinkedList<>();
        if(root == null){
            return list;
        }
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur=root;
        while(cur != null || !stack.isEmpty()){
            while(cur != null){
                list.add(cur.val);
                stack.push(cur);
                cur=cur.left;
            }
            TreeNode top=stack.pop();
            if(top!=null){
                cur=top.right;
            }
        }
       return list;
    }

十、二叉树中序非递归遍历

中序遍历的顺序是左-根-右，与上述前序遍历的思路基本一致，只不过在list添加的是每次出栈的元素，此是就符合中序遍历的顺序。

public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> list=new LinkedList<>();
        Stack<TreeNode> stack=new Stack<>();
        TreeNode cur=root;
        while(cur!=null||!stack.isEmpty()){
            while(cur!=null){
                stack.push(cur);
                cur=cur.left;
            }
            TreeNode top=stack.pop();
            list.add(top.val);
            cur=top.right;
        }
        return list;

    }

十一、二叉树后序非递归遍历

后序遍历的顺序是左-右-根，那么同样使用栈，定义一个结点cur指向root，一直遍历左子树，若为空则取栈顶元素top，若不为空cur就指向top的右子树进行遍历，否则就弹出元素，并加入到遍历集合list中，但是这样的话就会陷入循环会继续遍历右子树，于是增加一个perv记录每次弹出的元素，若top的右子树为空或top的右子树与prev相等就继续弹出元素进行遍历。

public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> list=new LinkedList<>();
        Stack<TreeNode> stack=new Stack<>();
        TreeNode cur=root;
        TreeNode prev = null;
        while(cur!=null||!stack.isEmpty()){
            while(cur!=null){
                stack.push(cur);
                cur=cur.left;
            }
            TreeNode top=stack.peek();
            if(top.right==null||prev==top.right ){
                TreeNode node = stack.pop();
                prev=node;
                list.add(node.val);
            }else{
                cur=top.right;
            }
        }
        return list;

    }