考研《数据结构》线性表

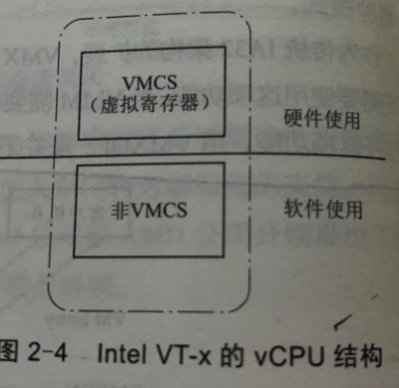
2.设计一个高效算法，将顺序表L的所有元素逆置，要求算法的空间复杂度为0（1）。

思路：扫描顺序表L的前半部分元素，对于元素L.data[i]与L.data[len-1-i]对换。

#include<iostream>
using namespace std;
const int maxn=100;
int len;
//定义顺序表
typedef struct
{
    int data[maxn];
    int length;
}Sqlist;
//实现逆置
void rev(Sqlist &l)//注意这里是引用传递
{

    int tem;
    for(int i=0;i<len/2;i++)
    {
        tem=l.data[i];
        l.data[i]=l.data[len-1-i];
        l.data[len-1-i]=tem;
    }
}
int main()
{
    Sqlist lis;
    cin>>len;//输入顺序表的长度
    for(int i=0;i<len;i++)
    {
        cin>>lis.data[i];
    }
    rev(lis);
    for(int i=0;i<len;i++)
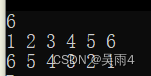
        cout<<lis.data[i]<<" ";
    return 0;
}

运行结果：

3.对长度为n的顺序表L 编写一个时间复杂度为0（n）、空间复杂度为0（1）的算法，该算法删除线性表中所有值为x的数据元素。

思路：用k记录顺序表L中不等于x的元素个数(即需要保存的元素个数)，扫描时将不等于X的元素移动到下标L的位置，并更新k值。

#include<iostream>
using namespace std;
const int maxn=100;
int len;
//定义了一个顺序表
typedef struct
{
    int data[maxn];
    int length;
}Sqlist;
//实现删除值为x的元素
void del_x(Sqlist &l,int x)
{
    int k;
    for(int i=0;i<len;i++)
    {
        if(l.data[i]!=x)//用掷不为x的元素覆盖顺序表，k表示顺序表现在的长度
        {
            l.data[k]=l.data[i];
            k++;
        }
    }
    len=k;
}
int main()
{
    Sqlist lis;
    cin>>len;//输入顺序表的长度
    for(int i=0;i<len;i++)
    {
        cin>>lis.data[i];
    }
    del_x(lis,3);//假设删除值为3的元素
    for(int i=0;i<len;i++)
        cout<<lis.data[i]<<" ";
    return 0;
}

运行结果：

4.从有序顺序表中删除其值在给定值s与t之间（包含s和t，要求s<t）的所有元素，若s或t不合理，或顺序表为空，则显示出错信息并退出运行。

思路：本题与上一题存在区别。因为是有序表，所以删除的元素必然是相连的整体。先寻找值大于等于s的第一个元素(第一个删除的元素)，然后寻找值大于t的第一个元素(最后一个删除的元素的下一个元素)，要将这段元素删除，只需直接将后面的元素前移。

#include<iostream>
using namespace std;
const int maxn=100;
int len;
typedef struct
{
    int data[maxn];
    int length;
}Sqlist;
bool del_s_t(Sqlist &l,int s,int t)
{
    int i,j;
    if(len==0||s>=t) return 0;//表为空，或者s、t不合法，则返回false
    for(i=0;i<len&&l.data[i]<s;i++);//找到第一个大于s的元素(删除的第一个元素)
    if(i>=len) return false;//所有元素都小于s，返回false
    for(j=i;j<len&&l.data[j]<=t;j++);//找到第一个大于t的元素(删除的最后一个元素的下一个)
    for(;j<len;i++,j++)
        l.data[i]=l.data[j];//用后面的元素覆盖上去
    l.length=i;
    len=l.length;
    return true;
}
int main()
{
    Sqlist lis;
    cin>>len;//输入顺序表的长度
    for(int i=0;i<len;i++)
    {
        cin>>lis.data[i];
    }
    del_s_t(lis,3,6);
    for(int i=0;i<len;i++)
        cout<<lis.data[i]<<" ";
    return 0;
}

运行结果：

5.从顺序表中删除其值在给定值s与t之间（包含s和t，要求s<t）的所有元素，若s或t不合理，或顺序表为空，则显示出错信息并退出运行。

思路：用k记录下元素值在s至t之间元素的个数，对于当前扫描的元素，若其值不在s到t之间，则前移k个位置；否则执行k++。

#include<iostream>
using namespace std;
const int maxn=100;
int len;
typedef struct
{
    int data[maxn];
    int length;
}Sqlist;
bool del_s_t(Sqlist &l,int s,int t)
{
    int k;
    l.length=len;
    if(len==0||s>=t) return 0;//表为空，或者s、t不合法，则返回false
    for(int i=0;i<len;i++)//遍历一遍顺序表
    {
        if(l.data[i]>=s&&l.data[i]<=t) k++;//记录要删除元素的个数
        else
            l.data[i-k]=l.data[i];//当前元素前移k个位置
    }
    l.length-=k;
    len=l.length;
    return true;
}
int main()
{
    Sqlist lis;
    cin>>len;//输入顺序表的长度
    for(int i=0;i<len;i++)
    {
        cin>>lis.data[i];
    }
    del_s_t(lis,3,6);
    for(int i=0;i<len;i++)
        cout<<lis.data[i]<<" ";
    return 0;
}

运行结果：

6.从有序顺序表中删除所有其值重复的元素，使表中所有元素的值均不同。

思路：注意是有序顺序表，值相同的元素一定在连续的位置上，用类似于直接插入排序的思想，初始时将第一个元素视为非重复的有序表。之后依次判断后面的元素是否与前面非重复有序表的最后一个元素相同，若相同，则继续向后判断，若不同，则插入前面的非重复有序表的最后，直至判断到表尾为止。

#include<iostream>
using namespace std;
const int maxn=100;
int len;
typedef struct
{
    int data[maxn];
    int length;
}Sqlist;
bool del_same(Sqlist &l)
{
    l.length=len;
    if(l.length==0) return false;
    int i,j;
    for(i=0,j=1;j<len;j++)
    {
        if(l.data[i]!=l.data[j]) l.data[++i]=l.data[j];
    }
    l.length=i+1;
    len=l.length;
    return true;
}
int main()
{
    Sqlist lis;
    cin>>len;//输入顺序表的长度
    for(int i=0;i<len;i++)
    {
        cin>>lis.data[i];
    }
    del_same(lis);
    for(int i=0;i<len;i++)
        cout<<lis.data[i]<<" ";
    return 0;
}

运行结果：

7.将两个有序顺序表合并为一个新的有序顺序表，并由函数返回结果顺序表。

思路：首先，双指针i、j，按顺序不断取下两个顺序表表头较小的结点存入新的顺序表中。然后，看哪个表还有剩余，将剩下的部分加到新的顺序表后面。

#include<iostream>
using namespace std;
const int maxn=100;
typedef struct
{
    int data[maxn];
    int length;
}Sqlist;
bool mergeab(Sqlist &lisa,Sqlist &lisb,Sqlist &lis)
{
    int i=0,j=0,k=0;
    if(lisa.length+lisb.length>lis.length) return false;
    while(i<lisa.length&&j<lisb.length)
    {
        if(lisa.data[i]<=lisb.data[j]) lis.data[k++]=lisa.data[i++];
        else lis.data[k++]=lisb.data[j++];
    }
    while(i<lisa.length) lis.data[k++]=lisa.data[i++];
    while(j<lisb.length) lis.data[k++]=lisb.data[j++];
    lis.length=k;
    return true;

}
int main()
{
    Sqlist lis,lisa,lisb;
    cin>>lisa.length>>lisb.length>>lis.length;//输入顺序表a,b的长度,顺序表lisb的元素
    for(int i=0;i<lisa.length;i++)//输入顺序表lisa的元素
    {
        cin>>lisa.data[i];
    }
    for(int i=0;i<lisb.length;i++)//输入顺序表lisb的元素
    {
        cin>>lisb.data[i];
    }
    mergeab(lisa,lisb,lis);
    for(int i=0;i<lis.length;i++)
        cout<<lis.data[i]<<" ";
    return 0;
}

运行结果：

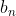8.已知在一维数组A[m+n]中依次存放两个线性表（a1,a2,..., $a_{m}$ ）和（b1, b2, ..., $b_{n}$ ）。编写一个函数，将数组中两个顺序表的位置互换，即将（b1, b2, ..., 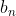$b_{n}$ ）放在（a1,a2,..., $a_{m}$ ）的前面。

思路：先将数组中的全部元素原地逆置,再对前n个元素和后m个元素分别使用逆置算法。

#include<iostream>
using namespace std;
const int maxn=100;
typedef struct
{
    int data[maxn];
    int length;
}Sqlist;
void rev(Sqlist &l,int st,int en)
{
    int tem;
    for(int i=st,j=en;j-i>=1;i++,j--)
    {
        tem=l.data[i];
        l.data[i]=l.data[j];
        l.data[j]=tem;
    }
}
int main()
{
    Sqlist lis;
    int m,n;
    cin>>m>>n;
    lis.length=m+n;
    for(int i=0;i<m;i++)//输入顺序表前m个元素
    {
        cin>>lis.data[i];
    }
    for(int i=m;i<m+n;i++)//输入顺序表前n个元素
    {
        cin>>lis.data[i];
    }
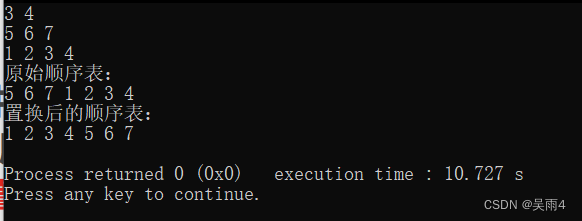
    cout<<"原始顺序表："<<endl;
    for(int i=0;i<lis.length;i++)
        cout<<lis.data[i]<<" ";
    cout<<endl;
    rev(lis,0,m+n-1);
    rev(lis,0,n-1);
    rev(lis,n,m+n-1);
    cout<<"置换后的顺序表："<<endl;
    for(int i=0;i<lis.length;i++)
        cout<<lis.data[i]<<" ";
    cout<<endl;
    return 0;
}

运行结果：

9.线性表（a1,a2,..., $a_{n}$ ）中的元素递增有序且按顺序存储于计算机内。要求设计一个算法，完成用最少时间在表中查找数值为x的元素，若找到，则将其与后继元素位置相交换，若找不到，则将其插入表中并使表中元素仍递增有序。

思路：顺序存储的线性表递增有序，可以顺序查找，也可以折半查找。题目要求“用最少的时间在表中查找数值为x的元素”，这里应使用折半查找法。

#include<iostream>
using namespace std;
const int maxn=100;
typedef struct
{
    int data[maxn];
    int length;
}Sqlist;
//二分查找元素x
void findx(Sqlist &l,int x)
{
    int left=0,right=l.length-1,mid;
    while(left<=right)
    {
        mid=left+right>>1;
        if(x==l.data[mid]) break;
        else if(x>l.data[mid]) left=mid+1;//在右侧
        else right=mid-1;//在左侧
    }
    if(l.data[mid]==x&&left!=l.length-1)//找到啦x，且不在最后一个位置，则可以与后继节点交换
    {
        int tem=l.data[mid];
        l.data[mid]=l.data[mid+1];
        l.data[mid+1]=tem;
    }
    //没有找到
    //由于经过二分查找之后，能确定x在right在右边，即在right的后插入x
    if(left>right)
    {
        int i;
        for(i=l.length-1;i>right;i--) l.data[i+1]=l.data[i];//元素后移
        l.data[i+1]=x;//插入x
        l.length+=1;//更新一下顺序表的长度
    }
}
int main()
{
    Sqlist lis;
    cin>>lis.length;
    for(int i=0;i<lis.length;i++)//输入顺序表前m个元素
    {
        cin>>lis.data[i];
    }
    int x;
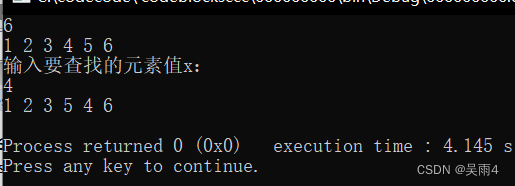
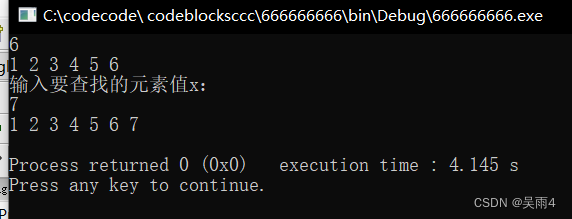
    cout<<"输入要查找的元素值x："<<endl;
    cin>>x;
    findx(lis,x);
    for(int i=0;i<lis.length;i++)
        cout<<lis.data[i]<<" ";
    cout<<endl;
    return 0;
}

运行结果：