1.题目

X 国王有一个地宫宝库，是 n×m 个格子的矩阵，每个格子放一件宝贝，每个宝贝贴着价值标签。

地宫的入口在左上角，出口在右下角。

小明被带到地宫的入口，国王要求他只能向右或向下行走。

走过某个格子时，如果那个格子中的宝贝价值比小明手中任意宝贝价值都大，小明就可以拿起它（当然，也可以不拿）。

当小明走到出口时，如果他手中的宝贝恰好是 $k$ 件，则这些宝贝就可以送给小明。

请你帮小明算一算，在给定的局面下，他有多少种不同的行动方案能获得这 $k$ 件宝贝

输入格式
第一行 3 个整数，$n,m,k$，含义见题目描述。

接下来 n 行，每行有 $m$ 个整数 $Ci$ 用来描述宝库矩阵每个格子的宝贝价值

输出格式
输出一个整数，表示正好取 $k$ 个宝贝的行动方案数。

该数字可能很大，输出它对 $1000000007$ 取模的结果。

数据范围
$1\le n,m\le 50,$
$1\le k\le 12,$
$0\le Ci\le 12$

输入样例1：

2 2 2
1 2
2 1

输出样例1：

2

输入样例2：

2 3 2
1 2 3
2 1 5

输出样例2：

14

2.基本思想

动态规划
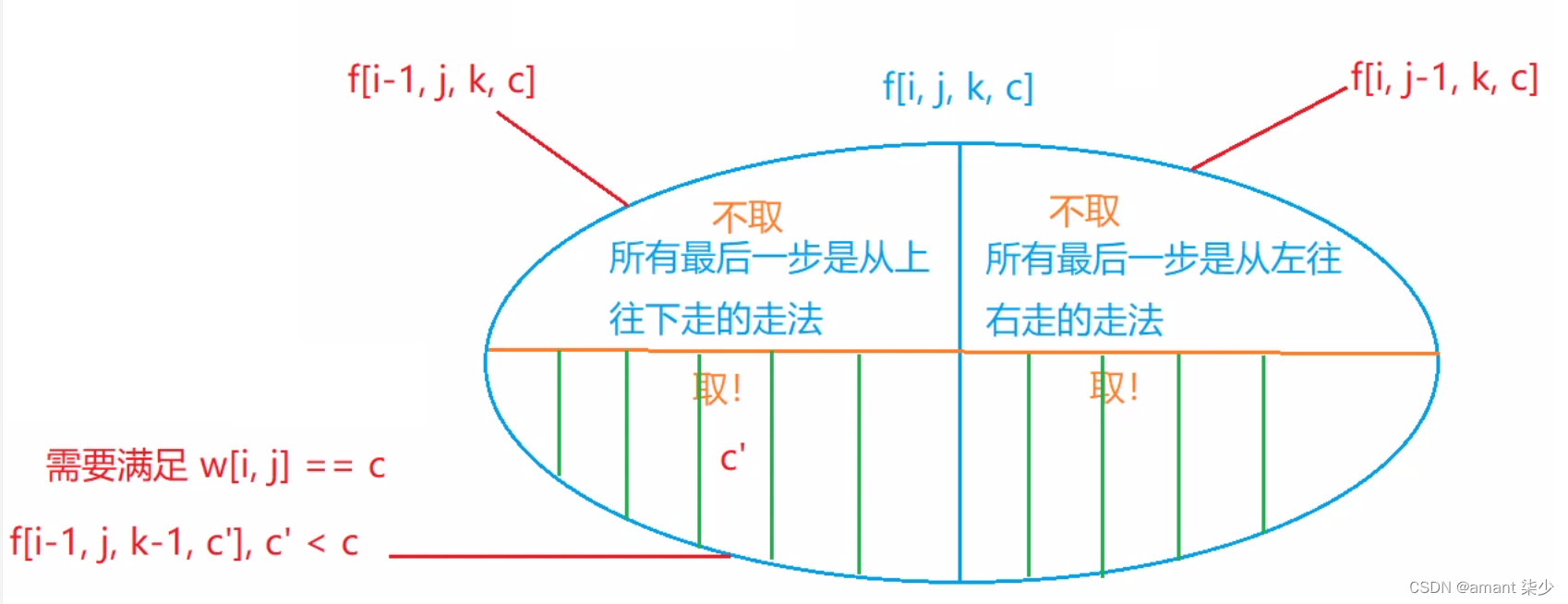
1.状态表示:

1.1集合：$f[i][j][k][c]$:所有从起点走到$（i，j）$且已经取了 $k$ 件物品且最后一件物品是$c$的合法的方案集合.
1.2属性：count

2.状态计算

Tips:

• 1.因为这道题的所有物品价值范围是0…12，可以把他们全部都递增，范围就变成了1…13，因为我们记录的是方案数，只关心各个物品之间的大小关系，具体数值不影响答案，但是这样的做法可以把0作为一个特殊边界来处理 (即当起点（1，1）不取时)
• 2.缝合怪
  本题目结合：摘花生（所有最最后一步从上往下走的走法$/$所有最后一步从左往右走的走法）+ 最长上升子序列+01背包（取$/$不取）

3.代码实现

public class _1212地宫取宝 {
    static Scanner sc = new Scanner(System.in);
    static int MOD = 1000000007;

    public static void main(String[] args) {
        int n = sc.nextInt();//行
        int m = sc.nextInt();//列
        int k = sc.nextInt();//件数
        int w[][] = new int[n+1][m+1];//价值
        int dp[][][][] = new int[55][55][13][14];   //个数：0~12 价值-1~12 此处-1为了方便初始化起点（1，1）处选择不取时
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                w[i][j] = sc.nextInt();
                w[i][j]++;//偏移量+1 价值-1~12 变为 0~13
            }
        }
        //两个边界初始化
        // 在起点 (1, 1) 处如果拿也只能拿 a[i][j] 这个物品，只有一种方案
        // 如果不拿，那就是 0 个物品，也是一个方案数由于物品价值已经增加了一个偏移量，现在价值的范围是 [1, 13]
        // 所以价值为 0 并不代表物品的价值，而是一个边界点
        dp[1][1][1][w[1][1]] = 1;//第一个 取
        dp[1][1][0][0] = 1;//不取

        //循环所有状态
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                if (i == 1 && j == 1) continue;//起点已经做过
                for (int u = 0; u <= k; u++) {
                    for (int v = 0; v <= 13; v++) {
                        // 不取物品
                        dp[i][j][u][v] = (dp[i][j][u][v]+dp[i-1][j][u][v])%MOD;
                        dp[i][j][u][v] = (dp[i][j][u][v]+dp[i][j-1][u][v])%MOD;//不能直接三个数 相加10^8+10^8+10^8可能会爆int(2.1*10^8)
                        //取
                        if (u>0 && v==w[i][j]){
                            for (int s = 0; s < v; s++) {//枚举c‘
                                dp[i][j][u][v]=(dp[i][j][u][v]+dp[i-1][j][u-1][s])%MOD;
                                dp[i][j][u][v]=(dp[i][j][u][v]+dp[i][j-1][u-1][s])%MOD;
                            }
                        }
                    }
                }
            }
        }
        int res=0;
        for (int i = 0; i <=13 ; i++)
            res=(res+dp[n][m][k][i])%MOD;
        System.out.println(res);
    }
}