三角测量法恢复深度

news2024/10/7 14:30:06

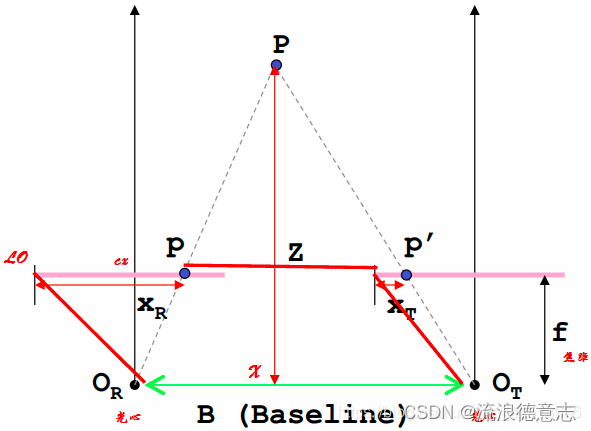
参考：单目vo中的深度确定方法--三角测量_单目相机三角测量-CSDN博客

方法一：直接法

由于我们已经通过本质矩阵分解或者单应矩阵分解获得了R与t，此时想求的是两个特征点的深度

bool depthFromTriangulation(
    const SE3& T_search_ref,
    const Vector3d& f_ref,
    const Vector3d& f_cur,
    double& depth)
{
    Matrix<double,3,2> A;
    A << T_search_ref.rotation_matrix()*f_ref, f_cur;
    const Matrix2d AtA = A.transpose()*A;
    if(AtA.determinant() < 0.000001)
        return false;
    const Vector2d depth2 = - AtA.inverse()*A.transpose()*T_search_ref.translation();
    depth = fabs(depth2[0]);
    return true;
}

方法二：Cramer法则

    // 方程
    // d_ref * f_ref = d_cur * ( R_RC * f_cur ) + t_RC
    // => [ f_ref^T f_ref, -f_ref^T f_cur ] [d_ref] = [f_ref^T t]
    //    [ f_cur^T f_ref, -f_cur^T f_cur ] [d_cur] = [f_cur^T t]
    // 二阶方程用克莱默法则求解并解之
    Vector3d t = T_R_C.translation();
    Vector3d f2 = T_R_C.rotation_matrix() * f_curr; 
    Vector2d b = Vector2d ( t.dot ( f_ref ), t.dot ( f2 ) );
    // 此处计算出系数矩阵A
    double A[4];
    A[0] = f_ref.dot ( f_ref );
    A[2] = f_ref.dot ( f2 );
    A[1] = -A[2];
    A[3] = - f2.dot ( f2 );
    // 此处计算A的行列式
    double d = A[0]*A[3]-A[1]*A[2];
    Vector2d lambdavec = 
        Vector2d (  A[3] * b ( 0,0 ) - A[1] * b ( 1,0 ),
                    -A[2] * b ( 0,0 ) + A[0] * b ( 1,0 )) /d;
    Vector3d xm = lambdavec ( 0,0 ) * f_ref;
    Vector3d xn = t + lambdavec ( 1,0 ) * f2;
    Vector3d d_esti = ( xm+xn ) / 2.0;  // 三角化算得的深度向量
    double depth_estimation = d_esti.norm();   // 深度值

方法三：OpenCV接口同方法二

void triangulation ( 
    const vector< KeyPoint >& keypoint_1, 
    const vector< KeyPoint >& keypoint_2, 
    const std::vector< DMatch >& matches,
    const Mat& R, const Mat& t, 
    vector< Point3d >& points )
{
    //相机第一个位置处的位姿
    Mat T1 = (Mat_<float> (3,4) <<
        1,0,0,0,
        0,1,0,0,
        0,0,1,0);
    //相机第二个位置处的位姿
    Mat T2 = (Mat_<float> (3,4) <<
        R.at<double>(0,0), R.at<double>(0,1), R.at<double>(0,2), t.at<double>(0,0),
        R.at<double>(1,0), R.at<double>(1,1), R.at<double>(1,2), t.at<double>(1,0),
        R.at<double>(2,0), R.at<double>(2,1), R.at<double>(2,2), t.at<double>(2,0)
    );
    
    // 相机内参
    Mat K = ( Mat_<double> ( 3,3 ) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1 );
    vector<Point2f> pts_1, pts_2;
    for ( DMatch m:matches )
    {
        // 将像素坐标转换至相机平面坐标，为什么要这一步，上面推导中有讲
        pts_1.push_back ( pixel2cam( keypoint_1[m.queryIdx].pt, K) );
        pts_2.push_back ( pixel2cam( keypoint_2[m.trainIdx].pt, K) );
    }
    
    Mat pts_4d;
    //opencv提供的三角测量函数
    cv::triangulatePoints( T1, T2, pts_1, pts_2, pts_4d );
    
    // 转换成非齐次坐标
    for ( int i=0; i<pts_4d.cols; i++ )
    {
        Mat x = pts_4d.col(i);
        x /= x.at<float>(3,0); // 归一化
        Point3d p (
            x.at<float>(0,0), 
            x.at<float>(1,0), 
            x.at<float>(2,0) 
        );
        points.push_back( p );
    }
}
 
Point2f pixel2cam ( const Point2d& p, const Mat& K )
{
    return Point2f
    (
        ( p.x - K.at<double>(0,2) ) / K.at<double>(0,0), 
        ( p.y - K.at<double>(1,2) ) / K.at<double>(1,1) 
    );
}

方法四：最小二乘法

// vins中初始化sfm时根据一个三维点在两帧中的投影位置确定三维点位置
void GlobalSFM::triangulatePoint(Eigen::Matrix<double, 3, 4> &Pose0, Eigen::Matrix<double, 3, 4> &Pose1,
						Vector2d &point0, Vector2d &point1, Vector3d &point_3d)
{
	Matrix4d design_matrix = Matrix4d::Zero();
	design_matrix.row(0) = point0[0] * Pose0.row(2) - Pose0.row(0);
	design_matrix.row(1) = point0[1] * Pose0.row(2) - Pose0.row(1);
	design_matrix.row(2) = point1[0] * Pose1.row(2) - Pose1.row(0);
	design_matrix.row(3) = point1[1] * Pose1.row(2) - Pose1.row(1);
	Vector4d triangulated_point;
	triangulated_point =
		      design_matrix.jacobiSvd(Eigen::ComputeFullV).matrixV().rightCols<1>();
	point_3d(0) = triangulated_point(0) / triangulated_point(3);
	point_3d(1) = triangulated_point(1) / triangulated_point(3);
	point_3d(2) = triangulated_point(2) / triangulated_point(3);
}