R-Tree的简单介绍

news2024/10/7 16:21:58

一、R-Tree简介

R-Tree，全称是“Real Tree”，是一种专门为处理多维空间数据（尤其是二维空间数据，如地理坐标）设计的树形数据结构。

简单来说，它就像是一个特殊的目录，将空间数据按照它们的位置和大小进行分组，存储在一系列的矩形区域（称为“节点”）中。每个节点不仅包含空间数据本身，还包含一个能完全覆盖其内部所有数据的矩形边界。这样，当我们查询某个特定区域内的数据时，R-Tree可以通过比较查询区域与节点矩形边界的关系，快速筛选出可能包含所需数据的节点，再逐层深入到更细粒度的节点进行精确查找，大大减少了需要检查的数据量。

二、R-Tree的结构特点

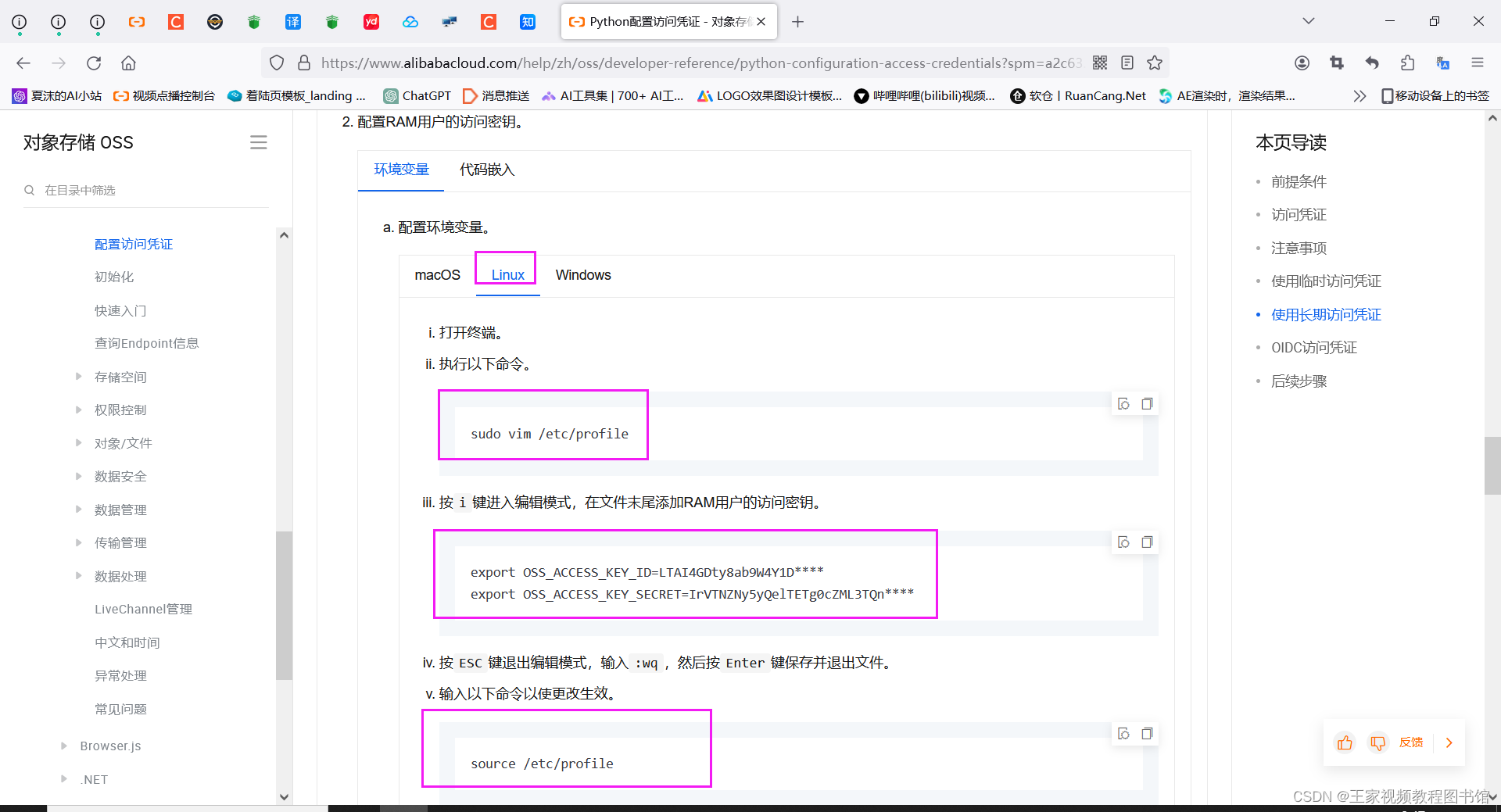
1. 分层结构：R-Tree就像一棵倒立的树，根节点在最上方，叶节点在最下方。根节点包含最少的数据，而叶节点包含最多的数据。每个非叶节点（内部节点）代表一个矩形区域，其子节点（可能是内部节点或叶节点）的矩形区域完全被父节点的矩形区域所覆盖。

2. 节点填充因子：为了保证查询效率，R-Tree通常会限制每个节点容纳的数据数量或其矩形区域的面积。这个比例被称为“填充因子”。合理的填充因子既能减少查询时需要检查的节点数量，又能避免树的高度过高，导致查询效率下降。

3. 超矩形划分：R-Tree的核心在于如何将空间数据划分为大小适中、相互覆盖关系合理的超矩形。常见的划分方法有最小边界矩形（MBR，Minimum Bounding Rectangle）、最小面积包围盒（Min-Area Bounding Box）等。

三、R-Tree的底层实现

1. 插入操作：当向R-Tree插入一个新数据时，需要找到一个合适的叶节点来存放。首先从根节点开始，沿着树向下遍历，直到找到一个与新数据边界有重叠的叶节点。然后，检查该节点是否已满（根据填充因子判断）。如果不满，直接将新数据加入；如果已满，则需要对该节点进行分裂，形成两个新的节点，将部分数据和新数据均匀分配到这两个节点中，并向上更新父节点的超矩形边界。如果父节点也因此满员，继续分裂和更新的过程，直至到达根节点。如果根节点也需要分裂，那么就创建一个新的根节点，将原来的根节点和新分裂的节点作为其子节点。

2. 查询操作：查询时，提供一个目标区域，从根节点开始，依次检查其子节点的超矩形边界是否与目标区域有重叠。如果有重叠，继续深入到子节点及其子孙节点进行相同的操作，直到到达叶节点。最后，收集所有与目标区域有重叠的叶节点中的数据，即为查询结果。

3. 删除操作：删除一个数据时，先找到包含该数据的叶节点，将其从节点中移除。如果移除后节点的数据量低于某个阈值（通常为填充因子的一半），可能需要进行节点合并或兄弟节点间的元素重平衡操作，以保持树的结构稳定和查询效率。

四、示例说明

示例1：插入操作

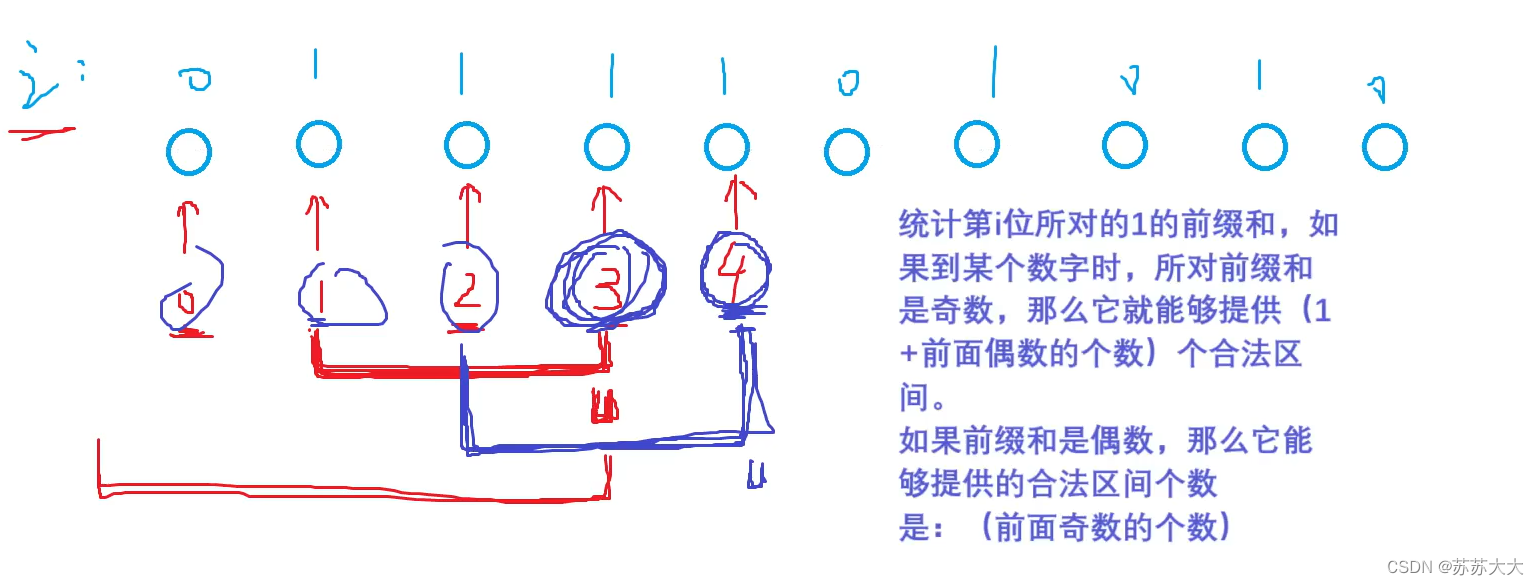
假设我们有一个空的R-Tree，现在要插入四个城市的位置（矩形边界）：北京、上海、广州、深圳。

  1. 首先，根节点为空，直接将北京插入，作为第一个叶节点。
  2. 插入上海，由于根节点未满，直接放入同一叶节点。
  3. 插入广州，根节点依然未满，放入同一叶节点。
  4. 插入深圳，此时叶节点已满（假设填充因子为1），需要分裂。将北京、上海分为一组，广州、深圳分为另一组，形成两个新的叶节点。更新根节点的超矩形边界，使其覆盖这两个新叶节点。

示例2：查询操作

假设我们要查询所有位于长江以南的城市。

  1. 从根节点开始，其超矩形边界包含了整个中国，与查询区域（长江以南）有重叠。
  2. 深入到包含广州和深圳的叶节点，其超矩形边界与查询区域有重叠，所以返回这两个城市。
  3. 继续深入到包含北京和上海的叶节点，其超矩形边界与查询区域无重叠，结束搜索。

示例3：删除操作

假设我们要删除广州。

  1. 找到包含广州的叶节点，将其从节点中移除。
  2. 由于该节点只剩下深圳一个数据，低于填充因子的一半，考虑合并或重平衡。假设选择合并，将相邻的北京、上海节点合并到此节点，形成一个新的叶节点，包含北京、上海、深圳三个城市，并更新父节点的超矩形边界。

 简单作答：

（简化的示例，没有涵盖完整的R-Tree实现细节（如节点分裂的具体算法、填充因子的管理等），旨在展示基本的插入逻辑。实际应用中，建议使用成熟的R-Tree库（如JTS Topology Suite或GeoTools））

Java版：

import java.awt.geom.Rectangle2D;
import java.util.ArrayList;
import java.util.List;

// 城市位置用矩形表示
class City {
    String name;
    Rectangle2D.Float rectangle;

    public City(String name, float x1, float y1, float x2, float y2) {
        this.name = name;
        this.rectangle = new Rectangle2D.Float(x1, y1, x2 - x1, y2 - y1);
    }

    @Override
    public String toString() {
        return name;
    }
}

// R-Tree节点
class RTreeNode {
    Rectangle2D.Float boundingBox;
    List<RTreeNode> children = new ArrayList<>();
    List<City> cities = new ArrayList<>();

    public RTreeNode(Rectangle2D.Float boundingBox) {
        this.boundingBox = boundingBox;
    }

    public void insertCity(City city) {
        // 此处仅模拟插入操作，简化版R-Tree直接将城市添加到当前节点
        cities.add(city);
        boundingBox = calculateBoundingBox(cities);
    }

    private static Rectangle2D.Float calculateBoundingBox(List<City> cities) {
        float xmin = Float.MAX_VALUE, ymin = Float.MAX_VALUE, xmax = Float.MIN_VALUE, ymax = Float.MIN_VALUE;
        for (var city : cities) {
            xmin = Math.min(xmin, (float) city.rectangle.getMinX());
            ymin = Math.min(ymin, (float) city.rectangle.getMinY());
            xmax = Math.max(xmax, (float) city.rectangle.getMaxX());
            ymax = Math.max(ymax, (float) city.rectangle.getMaxY());
        }
        return new Rectangle2D.Float(xmin, ymin, xmax - xmin, ymax - ymin);
    }

    public void addChild(RTreeNode child) {
        children.add(child);
        boundingBox = combineBoundingBoxes(boundingBox, child.boundingBox);
    }

    private static Rectangle2D.Float combineBoundingBoxes(Rectangle2D.Float bbox1, Rectangle2D.Float bbox2) {
        float xmin = Math.min(bbox1.getMinX(), bbox2.getMinX());
        float ymin = Math.min(bbox1.getMinY(), bbox2.getMinY());
        float xmax = Math.max(bbox1.getMaxX(), bbox2.getMaxX());
        float ymax = Math.max(bbox1.getMaxY(), bbox2.getMaxY());
        return new Rectangle2D.Float(xmin, ymin, xmax - xmin, ymax - ymin);
    }

    public List<City> query(Rectangle2D.Float queryArea) {
        var result = new ArrayList<City>();
        searchNodes(this, queryArea, result);
        return result;
    }

    private void searchNodes(RTreeNode node, Rectangle2D.Float queryArea, List<City> result) {
        if (queryArea.intersects(node.boundingBox)) {
            for (var child : node.children) {
                searchNodes(child, queryArea, result);
            }

            for (var city : node.cities) {
                if (queryArea.contains(city.rectangle)) {
                    result.add(city);
                }
            }
        }
    }

    public void removeCity(City city) {
        cities.remove(city);
        boundingBox = calculateBoundingBox(cities);
        if (cities.size() < 2) {  // 假设填充因子为1，最多容纳两个城市
            // 合并相邻节点（简化版R-Tree仅考虑相邻节点合并）
            if (!children.isEmpty()) {
                var firstChild = children.get(0);
                children.clear();
                cities.addAll(firstChild.cities);
                boundingBox = combineBoundingBoxes(boundingBox, firstChild.boundingBox);
                for (var grandchild : firstChild.children) {
                    addChild(grandchild);
                }
            }
        }
    }
}

// R-Tree类，包含根节点和操作方法
class RTree {
    public RTreeNode root;

    public RTree() {
        root = new RTreeNode(new Rectangle2D.Float(0, 0, .png, 1000));  // 假设根节点包含整个中国
    }

    public void insertCity(City city) {
        root.insertCity(city);
    }

    public List<City> query(Rectangle2D.Float queryArea) {
        return root.query(queryArea);
    }

    public void removeCity(City city) {
        root.removeCity(city);
    }
}

public class Main {
    public static void main(String[] args) {
        // 创建R-Tree实例并插入城市（与示例1相同）
        RTree rTree = new RTree();
        rTree.insertCity(new City("北京", 100, 100, 200, 200));
        rTree.insertCity(new City("上海", 300, 300, 400, 400));
        rTree.insertCity(new City("广州", 500, 500, 600, 600));
        rTree.insertCity(new City("深圳", 700, 700, 800, 800));

        // 示例2查询操作
        // 假设长江以南的查询区域为：(x1, y1) = (0, 0), (x2, y2) = (1000, ½ height of China)
        float queryHeight = 500;  // 示例中未提供中国高度，此处假设为500
        Rectangle2D.Float queryArea = new Rectangle2D.Float(0, 0, 1000, queryHeight);

        var result = rTree.query(queryArea);
        System.out.println("Cities located in the south of the Yangtze River:");
        for (var city : result) {
            System.out.println(city);
        }

        // 示例3删除操作
        rTree.removeCity(new City("广州", 500, 500, 600, 600));
    }
}

我们创建了一个接近实际R-Tree结构的简化实现，包括节点的层级结构（尽管在这个简化版本中，所有城市都直接存储在根节点中）和插入、查询、删除方法。RTreeNode类包含节点的边界、子节点列表和城市列表，以及计算边界、搜索节点、合并边界、插入城市、查询、删除城市等方法。RTree类包含根节点和对应的插入、查询、删除方法。

在Main方法中，我们首先创建一个RTree实例并插入四个城市（与示例1相同）。然后，我们根据示例2的描述定义了一个查询区域，表示长江以南的部分。接着，我们调用query方法进行查询，并打印出位于查询区域内的城市名称。最后，我们根据示例3的描述删除城市广州，并触发节点合并。

C++版：

#include <iostream>
#include <vector>
#include <algorithm>
#include <limits>

// 城市位置用矩形表示
struct City {
    std::string name;
    float x1, y1, x2, y2;

    City(const std::string& name, float x1, float y1, float x2, float y2)
        : name(name), x1(x1), y1(y1), x2(x2), y2(y2) {}
};

// R-Tree节点
class RTreeNode {
public:
    struct BoundingBox {
        float xmin, ymin, xmax, ymax;

        BoundingBox(float xmin, float ymin, float xmax, float ymax)
            : xmin(xmin), ymin(ymin), xmax(xmax), ymax(ymax) {}

        bool intersects(const BoundingBox& other) const {
            return !(other.xmax <= xmin || xmax <= other.xmin ||
                     other.ymax <= ymin || ymax <= other.ymin);
        }
    };

    std::vector<RTreeNode> children;
    std::vector<City> cities;
    BoundingBox boundingBox;

    void insertCity(const City& city) {
        // 此处仅模拟插入操作，简化版R-Tree直接将城市添加到当前节点
        cities.push_back(city);
        updateBoundingBox();
    }

    void addChild(const RTreeNode& child) {
        children.push_back(child);
        updateBoundingBox();
    }

    std::vector<City> query(const BoundingBox& queryArea) const {
        std::vector<City> result;
        searchNodes(*this, queryArea, result);
        return result;
    }

    void removeCity(const City& city) {
        auto it = std::find(cities.begin(), cities.end(), city);
        if (it != cities.end()) {
            cities.erase(it);
            updateBoundingBox();

            if (cities.size() < 2) {  // 假设填充因子为1，最多容纳两个城市
                // 合并相邻节点（简化版R-Tree仅考虑相邻节点合并）
                if (!children.empty()) {
                    children[0].cities.insert(children[0].cities.end(), cities.begin(), cities.end());
                    cities.clear();
                    boundingBox = children[0].boundingBox;
                    children.clear();
                }
            }
        }
    }

private:
    static BoundingBox calculateBoundingBox(const std::vector<City>& cities) {
        float xmin = std::numeric_limits<float>::max(), ymin = std::numeric_limits<float>::max(),
              xmax = std::numeric_limits<float>::min(), ymax = std::numeric_limits<float>::min();
        for (const auto& city : cities) {
            xmin = std::min(xmin, city.x1);
            ymin = std::min(ymin, city.y1);
            xmax = std::max(xmax, city.x2);
            ymax = std::max(ymax, city.y2);
        }
        return BoundingBox{xmin, ymin, xmax, ymax};
    }

    void updateBoundingBox() {
        boundingBox = calculateBoundingBox(cities);
        for (const auto& child : children) {
            boundingBox.xmin = std::min(boundingBox.xmin, child.boundingBox.xmin);
            boundingBox.ymin = std::min(boundingBox.ymin, child.boundingBox.ymin);
            boundingBox.xmax = std::max(boundingBox.xmax, child.boundingBox.xmax);
            boundingBox.ymax = std::max(boundingBox.ymax, child.boundingBox.ymax);
        }
    }

    static void searchNodes(const RTreeNode& node, const BoundingBox& queryArea, std::vector<City>& result) {
        if (node.boundingBox.intersects(queryArea)) {
            for (const auto& child : node.children) {
                searchNodes(child, queryArea, result);
            }

            for (const auto& city : node.cities) {
                if (queryArea.xmin <= city.x1 && city.x2 <= queryArea.xmax &&
                    queryArea.ymin <= city.y1 && city.y2 <= queryArea.ymax) {
                    result.push_back(city);
                }
            }
        }
    }
};

// R-Tree类，包含根节点和操作方法
class RTree {
public:
    RTreeNode root;

    RTree() {
        // 假设根节点包含整个中国
        root.boundingBox = RTreeNode::BoundingBox{0, 0, 1000, 1000};
    }

    void insertCity(const City& city) {
        root.insertCity(city);
    }

    std::vector<City> query(const RTreeNode::BoundingBox& queryArea) const {
        return root.query(queryArea);
    }

    void removeCity(const City& city) {
        root.removeCity(city);
    }
};

int main() {
    // 创建R-Tree实例并插入城市（与示例1相同）
    RTree rTree;
    rTree.insertCity({ "北京", 100, 100, 200, 200 });
    rTree.insertCity({ "上海", 300, 300, 400, 400 });
    rTree.insertCity({ "广州", 500, 500, 600, 600 });
    rTree.insertCity({ "深圳", 700, 700, 800, 800 });

    // 示例2查询操作
    // 假设长江以南的查询区域为：(x1, y1) = (0, 0), (x2, y2) = (1000, ½ height of China)
    float queryHeight = 500;  // 示例中未提供中国高度，此处假设为500
    RTreeNode::BoundingBox queryArea{0, 0, 1000, queryHeight};

    auto result = rTree.query(queryArea);
    std::cout << "Cities located in the south of the Yangtze River:" << std::endl;
    for (const auto& city : result) {
        std::cout << city.name << std::endl;
    }

    // 示例3删除操作
    rTree.removeCity({ "广州", 500, 500, 600, 600 });
    return 0;
}

在这个示例中，我们创建了一个接近实际R-Tree结构的简化实现，包括节点的层级结构（尽管在这个简化版本中，所有城市都直接存储在根节点中）和插入、查询、删除方法。

RTreeNode类包含节点的边界、子节点列表和城市列表，以及计算边界、搜索节点、插入城市、查询、删除城市等方法。RTree类包含根节点和对应的插入、查询、删除方法。

在main方法中，我们首先创建一个RTree实例并插入四个城市（与示例1相同）。然后，我们根据示例2的描述定义了一个查询区域，表示长江以南的部分。接着，我们调用query方法进行查询，并打印出位于查询区域内的城市名称。最后，我们根据示例3的描述删除城市广州，并触发节点合并。

C#版：

using System;
using System.Collections.Generic;
using System.Drawing;

// 城市位置用矩形表示
class City
{
    public string Name { get; set; }
    public RectangleF Rectangle { get; set; }

    public City(string name, float x1, float y1, float x2, float y2)
    {
        Name = name;
        Rectangle = new RectangleF(x1, y1, x2 - x1, y2 - y1);
    }
}

// R-Tree节点
class RTreeNode
{
    public RectangleF BoundingBox { get; set; }
    public List<RTreeNode> Children { get; } = new List<RTreeNode>();
    public List<City> Cities { get; } = new List<City>();

    public void InsertCity(City city)
    {
        // 此处仅模拟插入操作，简化版R-Tree直接将城市添加到当前节点
        Cities.Add(city);
        UpdateBoundingBox();
    }

    public void AddChild(RTreeNode child)
    {
        Children.Add(child);
        UpdateBoundingBox();
    }

    public List<City> Query(RectangleF queryArea)
    {
        var result = new List<City>();
        SearchNodes(this, queryArea, result);
        return result;
    }

    public void RemoveCity(City city)
    {
        Cities.Remove(city);
        UpdateBoundingBox();

        if (Cities.Count < 2)  // 假设填充因子为1，最多容纳两个城市
        {
            // 合并相邻节点（简化版R-Tree仅考虑相邻节点合并）
            if (Children.Count > 0)
            {
                Children[0].Cities.AddRange(Cities);
                Cities.Clear();
                BoundingBox = Children[0].BoundingBox;
                Children.Clear();
            }
        }
    }

    private void UpdateBoundingBox()
    {
        BoundingBox = CalculateBoundingBox(Cities);
        foreach (var child in Children)
        {
            BoundingBox = RectangleF.Union(BoundingBox, child.BoundingBox);
        }
    }

    private static RectangleF CalculateBoundingBox(List<City> cities)
    {
        float xmin = float.MaxValue, ymin = float.MaxValue, xmax = float.MinValue, ymax = float.MinValue;
        foreach (var city in cities)
        {
            xmin = Math.Min(xmin, city.Rectangle.X);
            ymin = Math.Min(ymin, city.Rectangle.Y);
            xmax = Math.Max(xmax, city.Rectangle.Right);
            ymax = Math.Max(ymax, city.Rectangle.Bottom);
        }
        return new RectangleF(xmin, ymin, xmax - xmin, ymax - ymin);
    }

    private static void SearchNodes(RTreeNode node, RectangleF queryArea, List<City> result)
    {
        if (queryArea.IntersectsWith(node.BoundingBox))
        {
            foreach (var child in node.Children)
            {
                SearchNodes(child, queryArea, result);
            }

            foreach (var city in node.Cities)
            {
                if (queryArea.Contains(city.Rectangle))
                {
                    result.Add(city);
                }
            }
        }
    }
}

// R-Tree类，包含根节点和操作方法
class RTree
{
    public RTreeNode Root { get; }

    public RTree()
    {
        // 假设根节点包含整个中国
        Root = new RTreeNode { BoundingBox = new RectangleF(0, 0, 1000, 1000) };
    }

    public void InsertCity(City city)
    {
        Root.InsertCity(city);
    }

    public List<City> Query(RectangleF queryArea)
    {
        return Root.Query(queryArea);
    }

    public void RemoveCity(City city)
    {
        Root.RemoveCity(city);
    }
}

class Program
{
    static void Main(string[] args)
    {
        // 创建R-Tree实例并插入城市（与示例1相同）
        RTree rTree = new RTree();
        rTree.InsertCity(new City("北京", 100, 100, 200, 200));
        rTree.InsertCity(new City("上海", 300, 300, 400, 400));
        rTree.InsertCity(new City("广州", 500, 500, 600, 600));
        rTree.InsertCity(new City("深圳", 700, 700, 800, 800));

        // 示例2查询操作
        // 假设长江以南的查询区域为：(x1, y1) = (0, 0), (x2, y2) = (1000, ½ height of China)
        float queryHeight = 500;  // 示例中未提供中国高度，此处假设为500
        RectangleF queryArea = new RectangleF(0, 0, 1000, queryHeight);

        var result = rTree.Query(queryArea);
        Console.WriteLine("Cities located in the south of the Yangtze River:");
        foreach (var city in result)
        {
            Console.WriteLine(city.Name);
        }

        // 示例3删除操作
        rTree.RemoveCity(new City("广州", 500, 500, 600, 600));
    }
}

在这个示例中，我们创建了一个接近实际R-Tree结构的简化实现，包括节点的层级结构（尽管在这个简化版本中，所有城市都直接存储在根节点中）和插入、查询、删除方法。

RTreeNode类包含节点的边界、子节点列表和城市列表，以及计算边界、搜索节点、插入城市、查询、删除城市等方法。RTree类包含根节点和对应的插入、查询、删除方法。

在Main方法中，我们首先创建一个RTree实例并插入四个城市（与示例1相同）。然后，我们根据示例2的描述定义了一个查询区域，表示长江以南的部分。接着，我们调用Query方法进行查询，并打印出位于查询区域内的城市名称。最后，我们根据示例3的描述删除城市广州，并触发节点合并。

注意：实际应用中，请使用成熟的R-Tree库以获得完整的功能和优化。

以上就是对R-Tree的详细介绍，包括其基本概念、结构特点、底层实现以及通过示例说明其插入、查询、删除操作。R-Tree作为一种高效的空间索引结构，极大地提升了大规模空间数据的检索效率，广泛应用于地理信息系统、搜索引擎、图像处理等领域。希望这次口语化的讲解能让大家对R-Tree有更深刻的理解。

如果有任何疑问，欢迎随时提问！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1581002.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

蝙蝠优化算法（bat optimization algorithm）

蝙蝠优化算法（bat optimization algorithm）

注意&#xff1a;本文引用自专业人工智能社区Venus AI 更多AI知识请参考原站 &#xff08;[www.aideeplearning.cn]&#xff09; 算法背景 蝙蝠优化算法&#xff08;Bat Algorithm&#xff09;是一种基于群体智能的优化算法&#xff0c;它的灵感来源于蝙蝠捕食时的回声定位行…
阅读更多...
蓝桥杯刷题-15-异或和之和-拆位+贡献法⭐⭐(⊙o⊙)

蓝桥杯刷题-15-异或和之和-拆位+贡献法⭐⭐(⊙o⊙)

蓝桥杯2023年第十四届省赛真题-异或和之和 题目描述 给定一个数组 Ai&#xff0c;分别求其每个子段的异或和&#xff0c;并求出它们的和。或者说&#xff0c;对于每组满足 1 ≤ L ≤ R ≤ n 的 L, R &#xff0c;求出数组中第 L 至第 R 个元素的异或和。然后输出每组 L, R 得到…
阅读更多...
Xlinx相关原语讲解导航页面

Xlinx相关原语讲解导航页面

原语就是对FPGA底层器件的直接调用&#xff0c;与IP功能是类似的&#xff0c;将原语的参数变成IP配置时的GUI界面参数&#xff0c;可能会更加直观。IP的缺陷在于繁杂&#xff0c;比如SelectIO IP内部包含IDDR、ODDR等等IO转换的功能&#xff0c;如果只想使用单沿转双沿一个功能…
阅读更多...
Leetcode刷题-字符串详细总结（Java）

Leetcode刷题-字符串详细总结（Java）

字符串 字符串可能在算法处理上面和数组是类似的&#xff0c;但是String和数组的数据结构还是有一些不一样的 1、反转字符串 344. 反转字符串 - 力扣&#xff08;LeetCode&#xff09; 双指针的经典应用&#xff0c;两个指针同时向中间移动 public void reverseString(char[…
阅读更多...
C语言进阶课程学习记录-第20课 - 链接过程简介

C语言进阶课程学习记录-第20课 - 链接过程简介

C语言进阶课程学习记录-第20课 - 链接过程简介 链接器静态链接实验-静态链接源代码生成目标文件打包生成静态库文件直接编译使用静态库编译 动态链接实验-动态链接源代码生成动态链接库文件直接编译使用动态链接库编译运行test.out删除dlib.so运行test.out 小结 本文学习自狄泰…
阅读更多...
【算法】二分算法题

【算法】二分算法题

个人主页 &#xff1a; zxctscl 如有转载请先通知 题目 1. 704. 二分查找1.1 分析1.2 代码 2. 34. 在排序数组中查找元素的第一个和最后一个位置2.1 分析2.2 代码 3. 35. 搜索插入位置3.1 分析3.2 代码 4. 852. 山脉数组的峰顶索引4.1 分析4.2 代码 5. 153. 寻找旋转排序数组中…
阅读更多...
nexus设置s3存储

nexus设置s3存储

问题 因为我的nexus是安装在EC2上面&#xff0c;需要利用s3的存储能力&#xff0c;为nexus提供存储服务。 步骤 准备s3桶 输入桶名&#xff0c;创建s3桶&#xff0c;如下图&#xff1a; 创建桶读写策略 具体内容如下&#xff1a; {"Version": "2012-10-1…
阅读更多...
【数据分享】我国第七次人口普查的100m分辨率人口栅格数据（免费获取\tif格式\2020年）

【数据分享】我国第七次人口普查的100m分辨率人口栅格数据（免费获取\tif格式\2020年）

人口空间分布数据是我们在各项研究中经常使用的数据。之前我们分享过来源于LandScan数据集的2000-2022年的1km精度的人口空间分布栅格数据&#xff08;可查看之前的文章获悉详情&#xff09;&#xff01; 相较于LandScan全球人口数据集&#xff0c;我国历次人口普查的数据对于…
阅读更多...
AI服务平台replicate

AI服务平台replicate

Replicate是一个提供优秀AI模型和工具的平台&#xff0c;旨在帮助用户实现各种人工智能任务。该平台汇集了来自各个领域的顶尖模型&#xff0c;涵盖了文本到图像生成、语言模型、图像编辑、超分辨率等多个领域。用户可以通过Replicate平台快速获取和应用先进的模型&#xff0c;…
阅读更多...
【C++】优先级队列（priority_queue）的用法与实现

【C++】优先级队列（priority_queue）的用法与实现

目录 一、概念&#xff1a; 二、仿函数&#xff08;Functor&#xff09;&#xff1a; 概念&#xff1a; 应用&#xff1a; 三、底层实现&#xff1a; 基本操作&#xff1a; 完整代码&#xff1a; 测试示例&#xff1a; 一、概念&#xff1a; 优先级队列&#xff08;pri…
阅读更多...
小白水平理解面试经典题目1431. Kids With the Greatest Number of Candies【Array类】

小白水平理解面试经典题目1431. Kids With the Greatest Number of Candies【Array类】

个人专栏 &#x1f93a; leetcode &#x1f9d7; Leetcode Prime &#x1f3c7; Golang20天教程 &#x1f6b4;‍♂️ Java问题收集园地 &#x1f334; 成长感悟 欢迎大家观看&#xff0c;不执着于追求顶峰&#xff0c;只享受探索过程 1431. 拥有最多糖果的孩子 小白渣翻译 一…
阅读更多...
蓝桥杯刷题-17-平方差-打表+数学⭐(⊙o⊙)

蓝桥杯刷题-17-平方差-打表+数学⭐(⊙o⊙)

之前的题目:最大也就到2e5左右。1e9的数据范围就意味着&#xff0c;即使是O(n)的复杂度&#xff0c;也会超时。此时可以考虑使用数学方法进行解题。 ❗打表:利用电脑去找一些合法答案&#xff0c;然后在这些合法答案中找规律。 ⭐打表后找到的规律: (1)好像所有的奇数都是合法…
阅读更多...
spikingjelly训练自己的网络---量化 --测试

spikingjelly训练自己的网络---量化 --测试

第二个 但是我发现&#xff0c;都要反量化&#xff0c;因为pytorch是只能支持浮点数的。 https://blog.csdn.net/lai_cheng/article/details/118961420 Pytorch的量化大致分为三种&#xff1a;模型训练完毕后动态量化、模型训练完毕后静态量化、模型训练中开启量化&#xff0c;…
阅读更多...
Java 解决 Process 执行命令行命令报【CreateProcess error=2, 系统找不到指定的文件。】错误问题

Java 解决 Process 执行命令行命令报【CreateProcess error=2, 系统找不到指定的文件。】错误问题

目录 问题 问题代码 解决方案 判断操作系统 问题 使用 Process 执行命令行命令时&#xff0c;报 CreateProcess error2, 系统找不到指定的文件。但明明指定的文件是存在的。而且这种错误只在 IDEA 中运行会报错&#xff0c;打包后直接 java -jar 运行就能正常运行&#xf…
阅读更多...
国产DSP FT-M6678开发-中断开发

国产DSP FT-M6678开发-中断开发

全局中断控制器&#xff08;CIC&#xff09; FT-M6678 芯片集成了众多的外设&#xff0c;这些外设都可产生中断事件源&#xff0c;这些中断事件如何被服务取决于用户的特殊应用。在FT-M6678 芯片中&#xff0c;EDMA 和CorePac 都能够为事件服务&#xff0c;为了最大限度的增加系…
阅读更多...
vue3第十六节（keep-alive 内置组件）

vue3第十六节（keep-alive 内置组件）

keep-alive 1、目的 在使用组件时&#xff0c;有时我们需要将组件进行缓存&#xff0c;而不是重新渲染&#xff0c;用以提高性能&#xff0c;避免重复加载DOM&#xff0c;提升用户的体验&#xff1b; keep-alive 组件可以做到这一点&#xff0c;它允许你缓存组件实例&#xf…
阅读更多...
家用洗地机哪个牌子好？四大热销机型推荐，值得推荐！

家用洗地机哪个牌子好？四大热销机型推荐，值得推荐！

随着科技的进步&#xff0c;洗地机在日常生活中能够帮助人们省时省力地打扫卫生&#xff0c;但市面上出现了各种各样的洗地机&#xff0c;好坏参差不齐&#xff0c;选择一个好品牌的洗地机非常重要&#xff0c;因为它们有着可靠的质量保证。那市面上如此众多的洗地机品牌&#…
阅读更多...
Python爬虫之分布式爬虫

Python爬虫之分布式爬虫

分布式爬虫 1.详情介绍 分布式爬虫是指将一个爬虫任务分解成多个子任务&#xff0c;在多个机器上同时执行&#xff0c;从而加快数据的抓取速度和提高系统的可靠性和容错性的技术。 传统的爬虫是在单台机器上运行&#xff0c;一次只能处理一个URL&#xff0c;而分布式爬虫通过将…
阅读更多...
关于阿里云centos系统下宝塔面板部署django/中pip install mysqlclient失败问题的大总结/阿里云使用oss长期访问凭证

关于阿里云centos系统下宝塔面板部署django/中pip install mysqlclient失败问题的大总结/阿里云使用oss长期访问凭证

python版本3.12.0 问题1 解决方案 sudo vim /etc/profile export MYSQLCLIENT_CFLAGS"-I/usr/include/mysql" export MYSQLCLIENT_LDFLAGS"-L/usr/lib64/mysql" Esc退出编辑模式 &#xff1a;wq退出并且保存 问题二 说是找不到 mysql.h头文件 CentOS ‘…
阅读更多...
【Python】不会优雅的记日志，你又又Out了！！！

【Python】不会优雅的记日志，你又又Out了！！！

1. 引言 在日常开发中&#xff0c;大家经常使用 print 函数来调试我们写的的代码。然而&#xff0c;随着打印语句数量的增加&#xff0c;由于缺乏行号或函数名称&#xff0c;很难确定输出来自何处。而且随着print语句的增多&#xff0c;调试完代码删除这些信息的时候也比较麻烦…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023