二分查找

介绍

一种复杂度为$O(logn)$级别的查找算法，需要被查找的数列具有某种单调性质，其本质其实是搜索一个符合check条件的区间。

二分分为两种：

• 整数二分
• 浮点数二分

核心思想：

首先讨论整数二分：

假设对从第l个数到第r个数的数列进行查找操作，取数列的中间的那个数，其下标向下取整则为mid = l + r >> 1，向上取整则为mid = l + r + 1 >> 1，根据题目条件，判断mid点是否满足check条件，满足则根据单调性质收缩区间为左区间或者右区间。

但是这里有两个问题，一个是选择向上取整还是向下取整，一个是收缩区间的端点是否包含mid。

这两种情况会引发不同的结果，这里采用两种方式的搭配：

• 找到数列中第一个满足check条件的点：向下取整，且mid点纳入右区间
• 找到数列中最后一个满足check条件的点：向上取整，且mid点纳入左区间

浮点数二分：

浮点二分较为简单，不需要考虑取整和区间选择的问题，即左右区间都可以容纳mid，因为浮点数的精度很高，只需要逐渐逼近题目要求的精度就可以了。这里需要注意的是，需要预先设定一个阈值eps，一般是比题目的精度还要高2位，比如题目要求的精度是1e-4，那么就可以设eps = 1e-6。

模板代码：

bool check(int x) // 检查x是否满足某种性质

// 整数二分：返回数列中第一个满足check条件的点
int binary_search1(int l, int r)
{
    // 区间[l, r]被划分成[l, mid]和[mid + 1, r]
	while(l < r)
    {
        int mid = l + r >> 1;
        if(check(mid)) r = mid;
        else l = mid + 1;
    }
    return r;
}

// 整数二分：返回数列中最后一个满足check条件的点
int binary_search2(int l, int r)
{
    // 区间[l, r]被划分成[l, mid]和[mid + 1, r]
    while(l < r)
    {
		int mid = l + r + 1 >> 1;
        if(check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

// 浮点数二分
double binary_search3(double l, double r)
{
    const double eps = 1e-6;
    while(r -l > eps)
    {
		double mid = (l + r)/2 ;
        if (check(mid)) r = mid;
        else l = mid;
    }
    return l;
}

例题1：

代码：

#include<iostream>
using namespace std;

const int N = 1e6 + 10;

int q[N], n, m, x;

int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (q[mid] >= x) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}

int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (q[mid] <= x) l = mid;
        else r = mid - 1;
    }
    return l;
}


int main()
{
    cin >> n >> m;
    for(int i=0; i<n; i++) scanf("%d", &q[i]);
    
    while(m--)
    {
        cin >> x;
        int l = bsearch_1(0, n-1);
        if(q[l] != x){cout << "-1 -1"<<endl;}
        else{
            cout << l << " " << bsearch_2(0, n-1) << endl;
        }
    }
    return 0;
}

例题2：

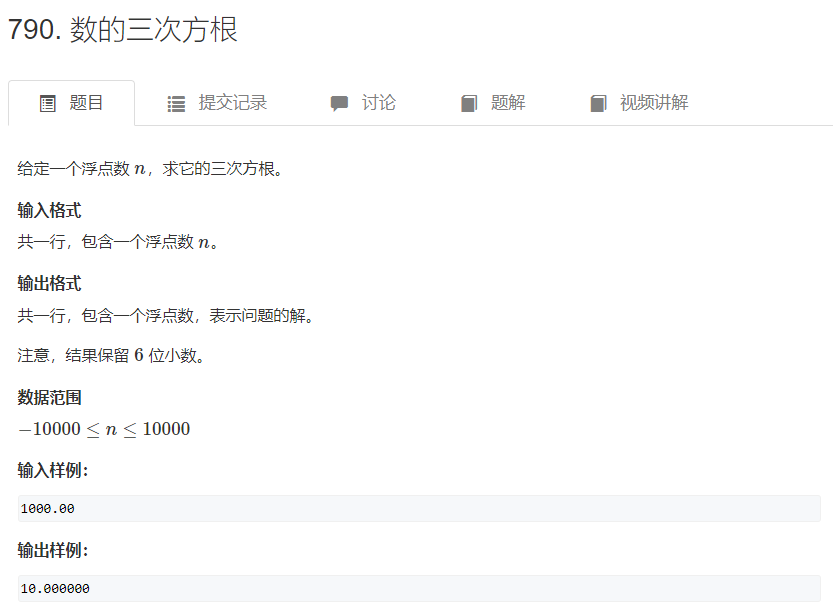
代码

#include<iostream>
using namespace std;
double n;

double binary_1(double l, double r)
{
    // cout << "l,r=" << l << "  " << r << endl;
    if(l >= r) return l; 
    double mid = (l+r)/2;
    if(mid*mid*mid < n) l = mid;
    else r = mid;
    
    if(r - l < 1e-8) return l;
    
    binary_1(l, r);
}

int main()
{
    cin >> n;
    double ans;
    if(n<0) cout << "-";
    
    n = abs(n);
    if(abs(n) >= 1) ans = binary_1(0, n);
    else ans = binary_1(n, 1);// ans = binary_1(0, 1)也可以，这样不需要思考边界
    printf("%.6lf", ans);
}