A. Joey Takes Money

给出一个序列a，每次操作可以选择两个数，将两个数分别改成与原数乘积相同的两个数，问最后得到的最大的数组和是多少。

思路：乘积一定，和最大一定是与1相乘。则整个数组的积与n - 1个1的和就是最大值。

AC Code：

#include <bits/stdc++.h>

typedef long long ll;
const int N = 1e5 + 5;
int t, n;
ll a[N];

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    std::cin >> t;
    while(t --) {
        std::cin >> n;
        ll sum = 1;
        for(int i = 1; i <= n; i ++) {
            std::cin >> a[i];
            sum *= a[i];
        }
        sum = (sum + (n - 1)) * 2022;
        std::cout << sum << '\n';
    }
    return 0;
}

B. Kill Demodogs

有n * n的矩阵，每个矩阵上有i * j个怪兽，每次可以向下移动一格或者向右移动一格，问从(1, 1)到(n, n)最多可以消灭多少怪兽。

思路：很显然，从中间走可以消灭最多的怪兽，这样就是两个数列求和，即通项为n * n的数列与n * (n + 1)的数列，化简得到的结果为(4 * n - 1) * (n + 1) * n * 337 % (1e9 + 7)。

AC Code：

#include <bits/stdc++.h>

typedef long long ll;
const int N = 1e5 + 5;
const int mod = 1e9 + 7;
int t;
ll n;

ll pmod(ll a, ll b) {
    ll res = 1;
    while(b) {
        if(b & 1) res = res * a % mod;
        b >>= 1;
        a = a * a % mod;
    }
    return res;
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    std::cin >> t;
    while(t --) {
        std::cin >> n;
        std::cout<< (4 * n - 1) * (n + 1) % mod * n % mod * pmod(6, mod - 2) % mod * 2022 % mod << '\n';
    }
    return 0;
}

C. Even Subarrays

给出一个数组a，求有多少子数组的异或和因数有偶数个。

思路：因数有奇数个的是完全平方数，所以我们枚举异或和为完全平方数的区间，逆向思维。注意时间复杂度，我们可以枚举数据范围内的完全平方数，mp记录一下即可。

AC Code：

#include <bits/stdc++.h>

typedef long long ll;
const int N = 4e5 + 5;
const int M = 2e6 + 5;
const int mod = 1e9 + 7;
#define int long long
int t, n;
int a[N], mp[M];

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    std::cin >> t;
    while(t --) {
        std::cin >> n;
        for(int i = 1; i <= n; i ++) {
            std::cin >> a[i];
            a[i] ^= a[i - 1];
        }
        for(int i = 0; i <= 2 * n; i ++) {
            mp[i] = 0;
        }
        mp[0] = 1;
        int ans = n * (n + 1) / 2;
        for(int i = 1; i <= n; i ++) {
            for(int j = 0; j * j <= n * 2; j ++) {
                int k = j * j;
                ans -= mp[a[i] ^ k];
            }
            mp[a[i]] ++;
        }
        std::cout << ans << '\n';
    }
    return 0;
}

D. Valiant's New Map

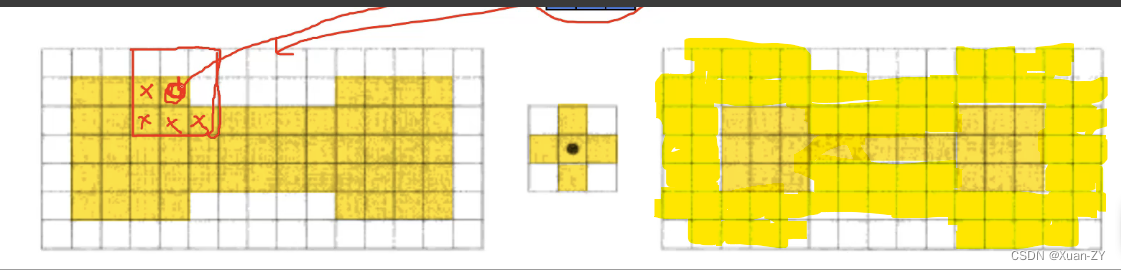
给出一个n * m的矩阵，求一个最大的l，满足矩阵中存在一个l * l的子矩阵，该子矩阵中每个数最小是l。

思路：一眼二分，二分前缀和处理，大于等于l的为1，否则为0，时间复杂度可行。

AC Code：

#include <bits/stdc++.h>

typedef long long ll;
#define int long long
const int N = 1e5 + 5;
int t, n, m;

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    std::cin >> t;
    while(t --) {
        std::cin >> n >> m;
        std::vector<std::vector<int> > a(n + 1, std::vector<int>(m + 1));
        for(int i = 1; i <= n; i ++) {
            for(int j = 1; j <= m; j ++) {
                std::cin >> a[i][j];
            }
        }
        auto check = [&](int mid) {
            std::vector<std::vector<int> > dif(n + 1, std::vector<int>(m + 1));
            for(int i = 1; i <= n; i ++) {
                for(int j = 1; j <= m; j ++) {
                    if(a[i][j] >= mid)
                        dif[i][j] = 1;
                    else
                        dif[i][j] = 0;
                }
            }
            for(int i = 1; i <= n; i ++) {
                for(int j = 1; j <= m; j ++) {
                    dif[i][j] += (dif[i - 1][j] + dif[i][j - 1] - dif[i - 1][j - 1]);
                }
            }
            for(int i = 1; i + mid - 1 <= n; i ++) {
                for(int j = 1; j + mid - 1 <= m; j ++) {
                    if(dif[i + mid - 1][j + mid - 1] - dif[i + mid - 1][j - 1] - dif[i - 1][j + mid - 1] + dif[i - 1][j - 1] == mid * mid)
                        return true;
                }
            }
            return false;
        };
        int l = 1, r = 1e6;
        while(l < r) {
            int mid = l + r + 1 >> 1;
            if(check(mid))
                l = mid;
            else
                r = mid - 1;
        }
        std::cout << l << '\n';
    }
    return 0;
}

E. Graph Cost

给n个点，问能否连出m个边。如果要连u和v那么边权为gcd(u, v)。每次可以连k个边权为k + 1的边，代价为k + 1，问最小代价。

思路：佬的思路！orzorz

AC Code：

#include <bits/stdc++.h>

typedef long long ll;
const int N = 1e6 + 5;
int t;
ll n, m, tot;
ll phi[N], prime[N], sz[N];
bool vis[N];

void getphi() {
    vis[0] = vis[1] = 1;
    phi[1] = 1;
    for(int i = 2; i <= N - 2; i ++) {
        if(!vis[i]) {
            prime[++ tot] = i;
            phi[i] = i - 1;
        }
        for(int j = 1; j <= tot; j ++) {
            if(i * prime[j] > N)
                break;
            vis[i * prime[j]] = 1;
            if(i % prime[j] == 0) {
                phi[i * prime[j]] = phi[i] * prime[j];
                break;
            }
            else
                phi[i * prime[j]] = phi[i] * (prime[j] - 1);
        }
    }
    phi[1] = 0;
    for(int i = 2; i <= N - 2; i ++) {
        phi[i] += phi[i - 1];
    }
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    getphi();
    std::cin >> t;
    while(t --) {
        std::cin >> n >> m;
        for(int i = 2; i <= n; i ++) {
            int res = n / i;
            sz[i] = phi[res];
        }
        ll ans = m;
        for(int i = n; i >= 2; i --) {
            ll h = sz[i] / (i - 1);
            ll c = std::min(h, (ll)m / (i - 1));
            ans += c;
            m -= (i - 1) * c;
        }
        if(m == 0)
            std::cout << ans << '\n';
        else
            std::cout << -1 << '\n';
    }
    return 0;
}