1.题目描述

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

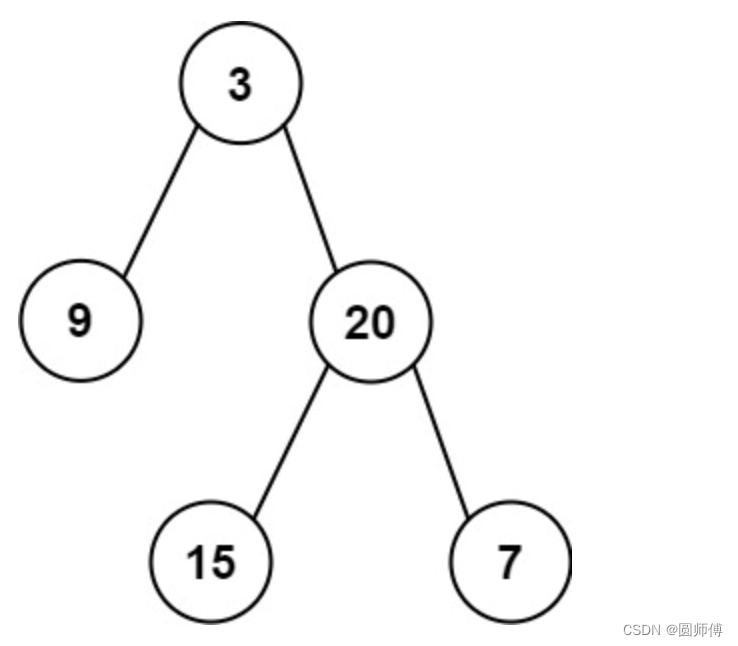
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

2. 分析

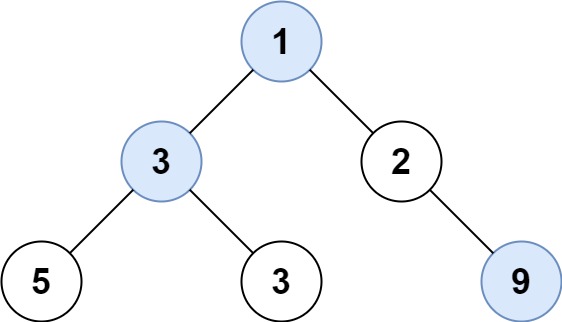
对于一颗普通的二叉树而言（如上图），我们知道的信息包括 根节点，左子树，右子树。遍历，就是每个节点都被访问了。

要解决这个问题，那么要明白下面的问题：

• 什么是前序遍历？
• 是什么中序遍历？
• 以及他们都有什么特点？

2.1 前序遍历

2.1.1 什么是前序遍历？

二叉树的前序遍历是一种常见的树遍历方法，用于按照根-左子树-右子树的顺序遍历二叉树的节点。
具体的前序遍历步骤如下：

• 1. 访问当前节点：首先访问二叉树的根节点。
• 2. 递归遍历左子树：如果当前节点有左子树，就递归地对左子树进行前序遍历，即重复步骤1和步骤2。
• 3. 递归遍历右子树：如果当前节点有右子树，就递归地对右子树进行前序遍历，即重复步骤1和步骤2。

以下是一个示例二叉树的前序遍历序列：1-2-4-5-3。

    1
   / \
  2   3
 / \
4   5

按照前序遍历的顺序，首先访问根节点1，然后遍历左子树，访问节点2，再遍历左子树，访问节点4，没有左子树后回溯到节点2，遍历右子树，访问节点5。最后回溯到根节点1后，遍历右子树，访问节点3。因此，前序遍历序列为1-2-4-5-3。

2.1.2 前序遍历有什么特点？

从前序遍历的结果可以看出：

• 1. 根节点在首位。
• 2. 后面紧跟着的是左子树和右子树。
• 3. 子树本身也符合根节点在首位，后面紧跟左右子树的特点。

2.2 中序遍历

2.2.1 什么是中序遍历

有了前门前序遍历的介绍，中序遍历就简单了。中序遍历就是先左节点-再根节点-最后右节点的方式遍历二叉树。

以下是一个示例二叉树的中序遍历序列：4-2-5-1-3。

    1
   / \
  2   3
 / \
4   5

按照中序遍历的顺序，首先遍历左子树，访问节点4，然后回溯到节点2，访问节点2本身，再遍历右子树，访问节点5。回溯到根节点1后，访问根节点1，再遍历右子树，访问节点3。因此，中序遍历序列为4-2-5-1-3。

2.2.2 中序遍历有什么特点？

• 1. 根节点的前面是左子树
• 2. 根节点的右面是右子树

2.3 后序遍历

2.3.1 什么是后序遍历？

后序遍历，那就是按左节点-右节点-根节点的方式遍历二叉树。
以下是一个示例二叉树的后序遍历序列：4-5-2-3-1。

    1
   / \
  2   3
 / \
4   5

按照后序遍历的顺序，首先遍历左子树，访问节点4，然后遍历右子树，访问节点5。回溯到根节点2后，访问节点2本身，然后遍历右子树，访问节点3。最后回溯到根节点1后，访问根节点1。因此，后序遍历序列为4-5-2-3-1。

2.3.2 特点

• 根节点在最后

2.4 总结

一颗确定的二叉树，有确定的前、中、后序遍历，但是单一的一个前中后序遍历，并不能确定一颗二叉树。要想确定这颗二叉树，那就需要两个遍历序列。

这里我们有了前序和中序遍历，那就可以根据特点推出完整二叉树：

前序遍历： 【3， 9， 20， 15， 7】
中序遍历： 【9， 3， 15， 20， 7】

首先根据前序遍历找到跟节点3， 那么中序遍历中根节点3前门的所有节点都是左子树节点。
由于前序遍历后面紧跟着左子树和右子树节点，根据数量，我们也可以分出前序遍历里左右子树的节点。
然后递归调用构建完整二叉树。

3. 解法

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {

    Map<Integer, Integer> indexMap;

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        int n = preorder.length;
        indexMap = new HashMap<>();

        for(int i = 0; i < n; i++) {
            indexMap.put(inorder[i], i);
        }

        return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);
    }

    private TreeNode myBuildTree(int[] preorder, int[] inorder, int preorderLeftIndex, int preorderRightIndex, int inorderLeftIndex, int inorderRightIndex) {
        if (preorderLeftIndex > preorderRightIndex) {
            return null;
        }

        int preorderRootIndex = preorderLeftIndex;
        int inorderRootIndex = indexMap.get(preorder[preorderRootIndex]);

        TreeNode root = new TreeNode(preorder[preorderRootIndex]);

        int leftSubtreeSize = inorderRootIndex - inorderLeftIndex;
        root.left = myBuildTree(preorder, inorder, preorderLeftIndex + 1, preorderLeftIndex + leftSubtreeSize, inorderLeftIndex, inorderRootIndex - 1);

        root.right = myBuildTree(preorder, inorder, preorderLeftIndex + leftSubtreeSize + 1, preorderRightIndex, inorderRootIndex + 1, inorderRightIndex);

        return root;

    }
}