算法实验课二
矩阵最小路径和
leetcode裸题
最小路径和
给定一个包含非负整数的 *m* x *n* 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例 1:
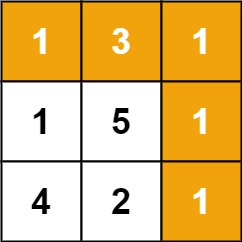
输入:grid = [[1,3,1],[1,5,1],[4,2,1]] 输出:7 解释:因为路径 1→3→1→1→1 的总和最小。
示例 2:
输入:grid = [[1,2,3],[4,5,6]] 输出:12
提示:
-
m == grid.length -
n == grid[i].length -
1 <= m, n <= 200 -
0 <= grid[i][j] <= 200
class Solution {
public:
//dp[i][j]代表该位置上的最小和
//dp[i][j] = dp[i-1][j]) if(grid[i-1][j] > )
int minPathSum(vector<vector<int>>& grid) {
int m = grid.size();//行数
int n = grid[0].size();//列数
vector<vector<int>> dp = grid;
for(int i = 1; i < m; i ++)
dp[i][0] = dp[i][0] + dp[i - 1][0];
for(int j = 1; j < n; j ++)
dp[0][j] = dp[0][j] + dp[0][j - 1];
for(int i = 1; i < m; i ++)
{
for(int j = 1; j < n; j ++)
{
dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + dp[i][j];
// dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
}
}
return dp[m - 1][n - 1];
}
};完整实现
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
typedef long long LL;
LL dp[N][N];
LL grid[N][N];
int n, m;
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= m; j ++)
{
cin >> grid[i][j];
dp[i][j] = grid[i][j];//初始化
}
for(int i = 1; i <= n; i ++)
dp[i][1] = dp[i][1] + dp[i - 1][0];
for(int j = 1; j <= m; j ++)
dp[1][j] = dp[1][j] + dp[1][j - 1];
for(int i = 1; i <= n; i ++)
{
for(int j = 1; j <= m; j ++)
{
dp[i][j] += min(dp[i - 1][j], dp[i][j - 1]);
}
}
cout << dp[n][m] << endl;
return 0;
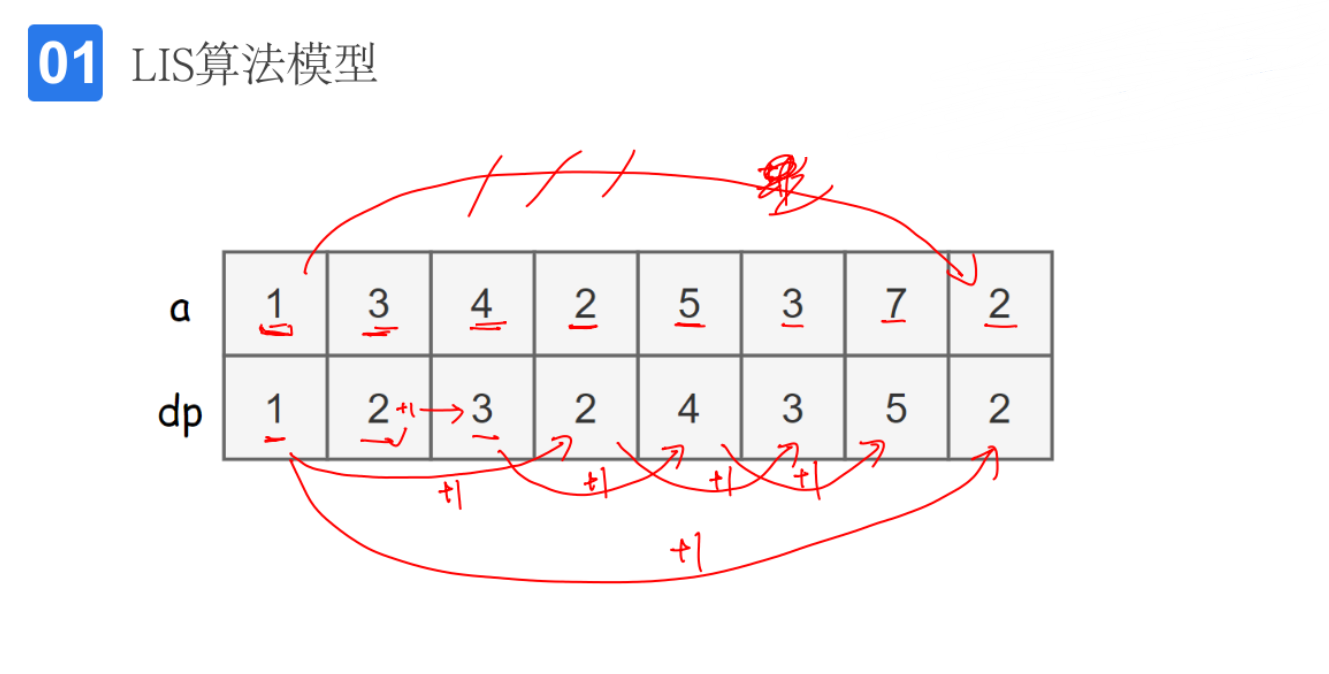
}LIS最长上升子序列

题目练习
1.蓝桥勇士
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int dp[N];//表示以a[i]结尾的最长上升子序列的长度
int a[N];
int n;
int main()
{
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
cin >> n;
for(int i = 1; i <= n; i ++)
{
cin >> a[i];
dp[i] = 1;//初始化
}
for(int i = 1; i <= n; i ++)
for(int j = 1; j < i; j ++)
if(a[j] < a[i])
dp[i] = max(dp[i], dp[j] + 1);//状态转移方程
int res = -0x3f3f3f3f;//答案初始为一个最小值
for(int i = 1; i <= n; i ++)//判断以哪个a[i]结尾是最长的上升子序列
res = max(res, dp[i]);
cout << res << endl;
return 0;
}
判断以哪个a[i]结尾是最长的上升子序列可以偷懒使用库函数
// int res = -0x3f3f3f3f;//答案初始为一个最小值 // for(int i = 1; i <= n; i ++)//判断以哪个a[i]结尾是最长的上升子序列 // res = max(res, dp[i]);
cout << *max_element(dp + 1, dp + 1 + n) << endl;
以上最长上升子序列(LIS)算法时间复杂度O(n^2)
还有一种实现方式,可以利用二分实现O(nlogn)的时间复杂度
题目二
1.合唱队形

代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int a[N], dp1[N], dp2[N], n;
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++)
{
cin >> a[i];
dp1[i] = 1;
dp2[i] = 1;
}
for(int i = 1; i <= n; i ++)
for(int j = 1; j < i; j ++)
if(a[j] < a[i])
dp1[i] = max(dp1[i], dp1[j] + 1);
for(int i = n; i ; i --)
for(int j = n; j > i; j --)
if(a[j] < a[i])
dp2[i] = max(dp2[i], dp2[j] + 1);
int res = -0x3f3f3f3f;
for(int i = 1; i <= n; i ++)
res = max(res, dp1[i] + dp2[i] - 1);
cout << n - res << endl;
return 0;
}leetcode裸题
300. 最长递增子序列 - 力扣(LeetCode)
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int dp[2550];
if(nums.size() == 0)
return 0;
for(int i = 0; i < nums.size(); i ++)
{
dp[i] = 1;//初始化
for(int j = 0; j < i; j ++)
if(nums[j] < nums[i])
dp[i] = max(dp[i], dp[j] + 1);
}
return *max_element(dp, dp + nums.size());
}
};