【问题描述】
小明每天都要练功，练功中的重要一项是梅花桩。
小明练功的梅花桩排列成 n 行 m 列，相邻两行的距离为 1，相邻两列的距离也为 1。
小明站在第 1 行第 1 列上，他要走到第 n 行第 m 列上。小明已经练了一段时间，他现在可以一步移动不超过 d 的距离（直线距离）。
小明想知道，在不掉下梅花桩的情况下，自己最少要多少步可以移动到目标。
【输入格式】
输入的第一行包含两个整数 n, m，分别表示梅花桩的行数和列数。
第二行包含一个实数 d（最多包含一位小数），表示小明一步可以移动的距离。
【输出格式】
输出一个整数，表示小明最少多少步可以到达目标。
【样例输入】
3 4
1.5
【样例输出】
3
【评测用例规模与约定】
对于 30% 的评测用例，2 <= n, m <= 20，1 <= d <= 20。
对于 60% 的评测用例，2 <= n, m <= 100，1 <= d <= 100。
对于所有评测用例，2 <= n, m <= 1000，1 <= d <= 100。

思路：根据题意可以采用广度优先搜索，将遍历过的点加入到一个队列，队列中的点距原点（1,1）的距离从小到大，每次从队首中取出结点进行拓展，直至拓展至终点。

要解决的问题：

①如何判断到达每个点的最小步数：用一个二维数组vis存储，vis[i][j]表示（1,1）到（i

，j）的最小步数，从（i，j）拓展出点（s，t），则令vis[s][t]=vis[i][j]+1，也就是步数加1

②如何拓展周围的点：读懂题目的值，只要我一步的距离小于d，我去哪都行，直着走也行，斜着走也行，就像是以点（i，j）为圆心，做半径为d的圆，圆里边的点我都可以拓展。那怎么判断哪些点在圆内呢？可以用两层for循环来遍历，然后判断那些点与圆心的距离是否小于d，来判断是否在圆内。不过这样时间复杂度就有点大了，可以贪心一下，如下图：

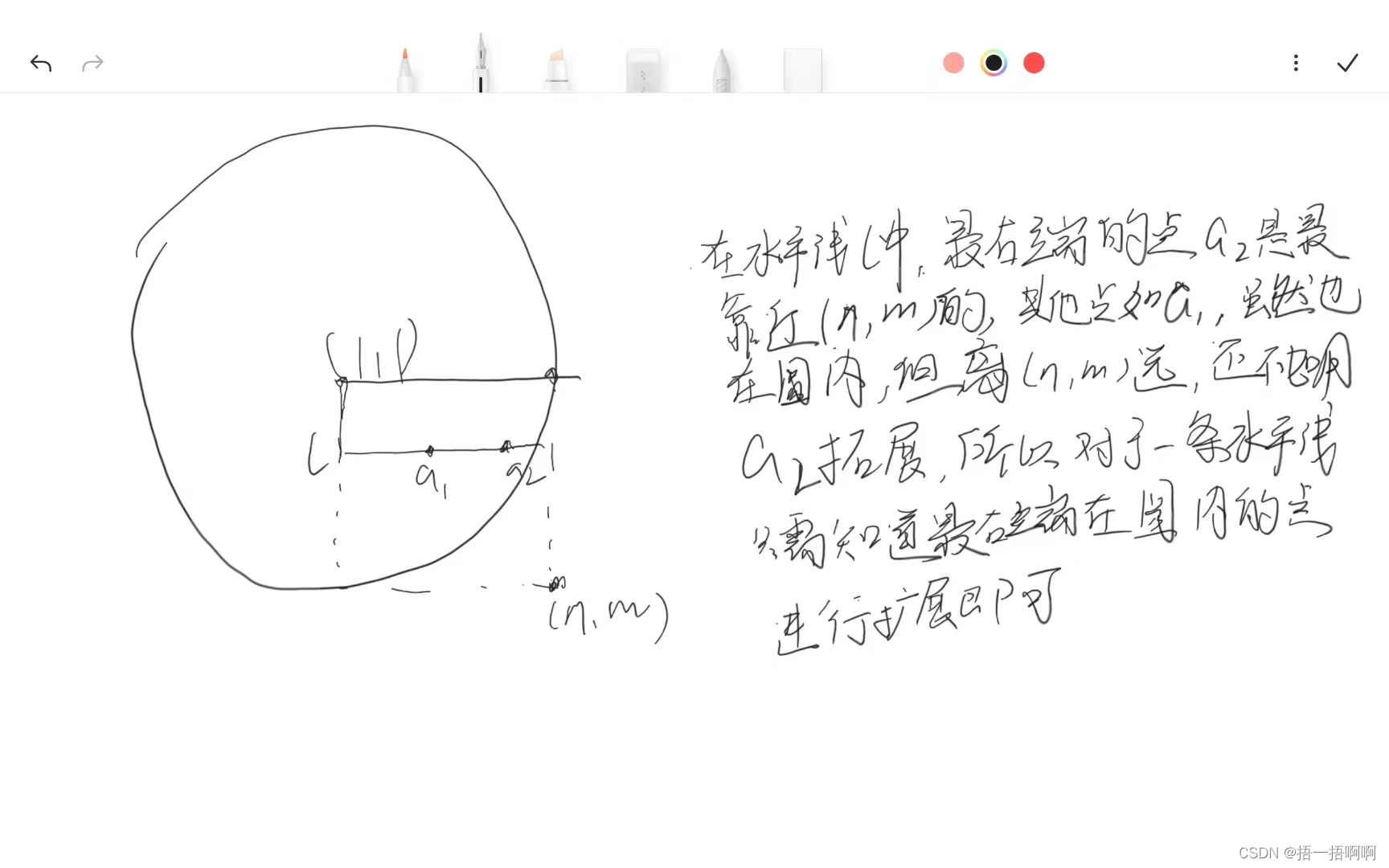
那怎么找一水平线最大能像右边拓展的点呢？用二分（从一堆与圆形距离小于等于d的点中找最大那个）

③通过上述思路，可以写出来代码，但是还是有一个测试点显示时间超时，那怎么优化呢？

可以想到，我们用一个点拓展出的其他点，步数都是一样的，那我只取距离终点（n，m）最近的那个放入队列再进行拓展不就好了

好了，问题应该就这些了，ac代码如下：

#include<bits/stdc++.h>
using namespace std;
int vis[1010][1010];
int n,m;
double d;
struct Point {
	int x,y;
};
double dis(int x1,int y1,int x2,int y2) {
	return sqrt(pow(x1-x2,2)+pow(y1-y2,2));
}
int bfs() {
	queue<Point>q;
	q.push({1,1});
	vis[1][1]=1;
	while(!q.empty()) {
		Point p=q.front();
		q.pop();
		if(d-dis(n,m,p.x,p.y)>-1e-6)return vis[p.x][p.y];//不用到终点，我只需要知道在某个点能不能一步到终点即可，如果能到，我直接得出结果，为什么这里不用加1，因为我的步数是从1开始的，所以自然多了一个1
		int x1=1,y1=1;
    double minDis=0x3f3f3f3f;
		for(int i=p.x; i<=min(p.x+d,n*1.0); i++) {
			//二分找y的最大值
			int mid;
			int l=p.y,r=min(m*1.0,p.y+d);
			while(l<r) {
				mid=(l+r+1)/2;
				if(d-dis(p.x,p.y,i,mid)>-1e-6)l=mid;
				else r=mid-1;
			}
			if(!vis[i][l]&&minDis>dis(i,l,n,m)) {
				x1=i,y1=l,minDis=dis(i,l,n,m);
			}
		}
		if(!vis[x1][y1]){//只拓展离终点最近的那个
			q.push({x1,y1});
			vis[x1][y1]=vis[p.x][p.y]+1;
		}
	}
	return -1;
}
int main() {
	cin>>n>>m;
	cin>>d;
	cout<<bfs()<<endl;
}