day60 动态规划part17

news2024/10/6 6:02:49

这两题看了自己写的笔记还不懂的话，看看这个up的思路就行：
https://space.bilibili.com/111062940/search/video?keyword=%E5%9B%9E%E6%96%87

647. 回文子串

中等
提示
给你一个字符串 s ，请你统计并返回这个字符串中回文子串的数目。

回文字符串是正着读和倒过来读一样的字符串。

子字符串是字符串中的由连续字符组成的一个序列。

具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。

网友1：

回文子串：需要是数组内部连续的。

dp数组含义：
以i为起始，以j为结尾的子串是否为回文。
递推公式：
当遍历到s【i】==s【j】时，就可以判断回文，有三种情况

a 此时i==j 一定是回文串
aa 此时 j-i=1 一定是回文串
j-i<=1 : dp【i】【j】=True
aba 此时j-i>1 ，需要判断内部【 i+1，j-1】是否为回文串，如果是，那么合起来就是回文串。
If dp【i+1】【j-1】==True; dp【i】【j】=True

初始化：
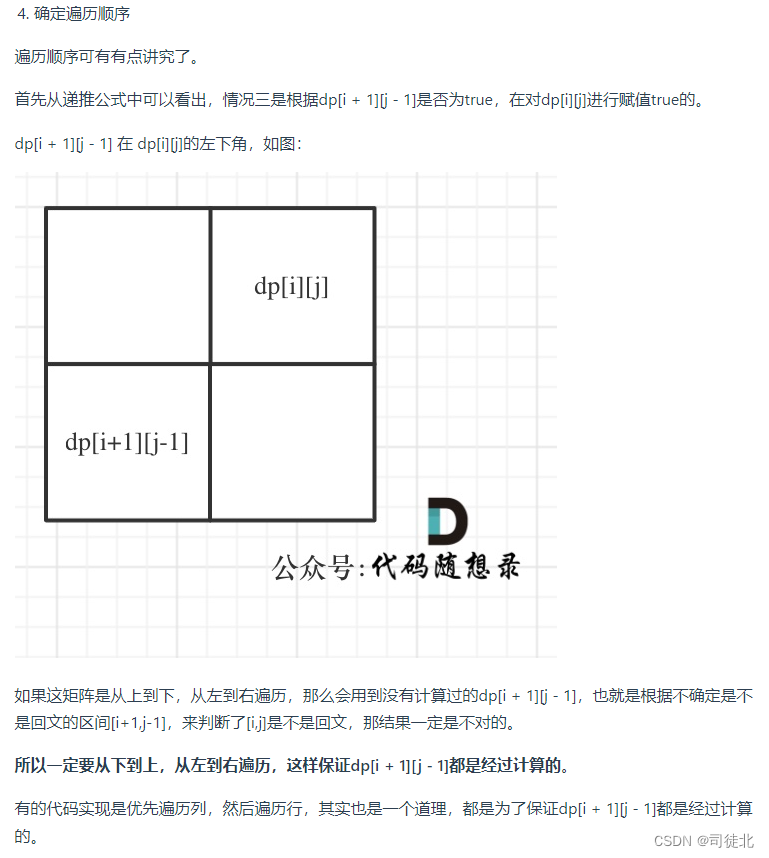
由于上面提及了 i=j的情况，所以将所有位置初始化为false即可
遍历顺序：
dp【i】【j】需要依赖 dp【i+1】【j-1】,所以i从大到小，j从小到大，并且j为i后面，所以j从i开始遍历。

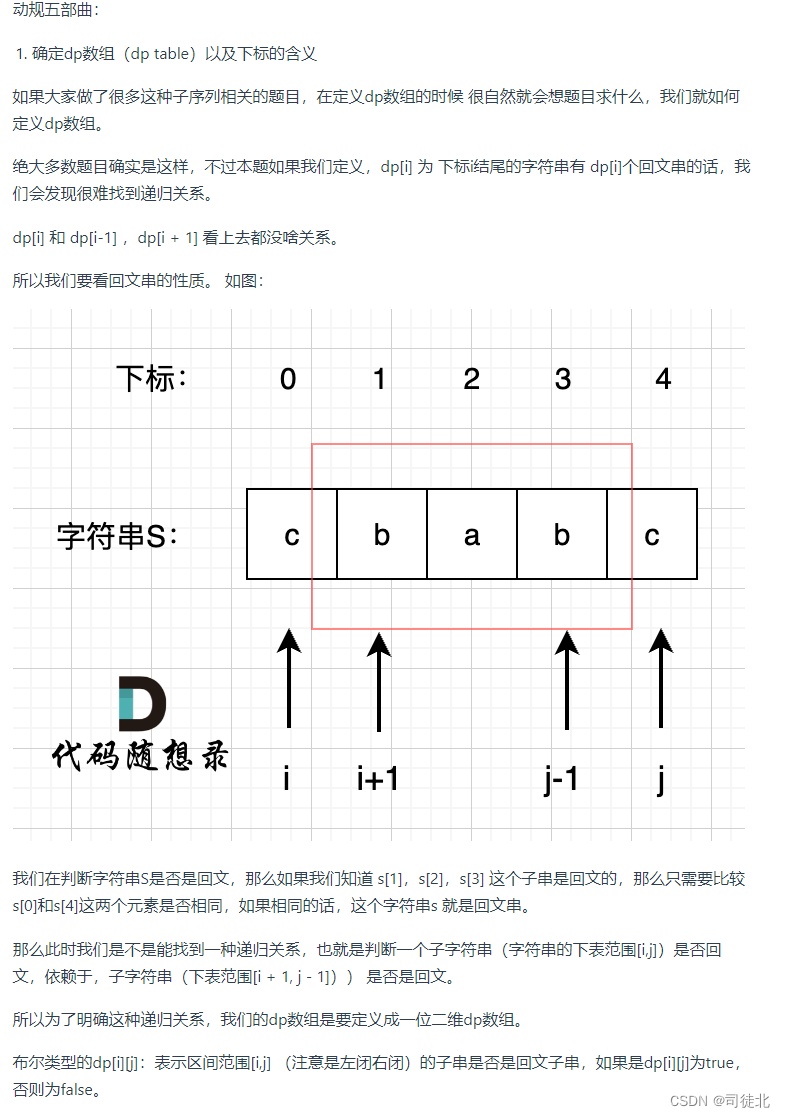
布尔类型的dp[i][j]：表示区间范围[i,j] （注意是左闭右闭）的子串是否是回文子串，如果是dp[i][j]为true，否则为false。dp[i][j]要把i理解为左指针left，j要理解为右指针right，如上图所示。所以遍历顺序一点也不奇怪了，先把right指向第二个元素，下标为1，然后left一直从0开始，始终小于右指针。初始化呢，一开始开辟空间全都是0，所以也不用初始化了。这题建议也可以看看代码随想录的解题思路，它的遍历顺序需要注意。

// dp[i + 1][j - 1] 从递推公式可以看出dp[i][j] 依赖于dp[i + 1][j - 1]，所以要先算比较大的i,i要从末尾开始算，i--，j要从小的开始算，j++
class Solution {
    public int countSubstrings(String s) {
        char[] chars = s.toCharArray();
        int len = chars.length;
        boolean[][] dp = new boolean[len][len];
        int result = 0;
        for (int i = len - 1; i >= 0; i--) { // i 是 left
            for (int j = i; j < len; j++) { // j 是 right
                if (chars[i] == chars[j]) { // 当这俩相等时
                    if (j - i <= 1) { // 说明是同一个字符或者两个挨着的字符 
                        result++;
                        dp[i][j] = true;
                    } else if (dp[i + 1][j - 1]) { // 相隔超过两个字符
                        result++;
                        dp[i][j] = true;
                    }
                    // 其他情况都是false，初始化就为false，不用管了
                }
            }
        }
        return result;
    }
}

516. 最长回文子序列

中等
给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。

子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。

class Solution {
    public int longestPalindromeSubseq(String s) {
        // dp[i][j]：字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]
        // 递推公式：如果s[i]与s[j]相同，那么dp[i][j] = dp[i + 1][j - 1] + 2
        // 根据递推公式可以看出，i要从后往前遍历（i要先计算大的），j要从前往后遍历（j要先计算小的）
        int len = s.length();
        int [][] dp = new int[len][len];
        // 递推公式决定了，left不可能访问到len - 1， right不可能访问到 0
        for (int i = 0; i < len; i++) dp[i][i] = 1;

        for (int l = len - 2; l >= 0; l--) {
            for (int r = l + 1; r < len; r++) {
                if (s.charAt(r) == s.charAt(l)) {
                    dp[l][r] = dp[l + 1][r - 1] + 2;
                } else {
                    dp[l][r] = Math.max(dp[l + 1][r], dp[l][r - 1]); // 也就是说，删掉首部字符或者尾部字符，取最大那种情况
                    // 比如说 acbac， 取前4个，acba或者后4个，cbac
                }
            }
        }

        return dp[0][len - 1];
    }
}