先了解什么是堆:
堆的定义
n个元素的序列 [ k1,k2,...,kn ],满足以下的性质时称之为堆:
ki≥k2i 且 ki≥k2i+1 (1≤i≤
)
或
ki≤k2i 且 ki≤k2i+1 (1≤i≤
)
如果采用顺序方式即用一维数组存储这个序列,就可以将这个序列的每一个元素ki看成是一棵有n个结点的完全二叉树的第i个结点,其中k1是该二叉树的根结点。
把堆对应的一维数组(即该序列的顺序存储结构)看作一棵完全二叉树的顺序存储,那么堆的特征可解释为:
1、完全二叉树中任一分支结点的值都小于等于或大于等于它的左、右孩子结点的值。
2、堆的元素序列中的第一个元素k1,即对应的完全二叉树根结点的值是所有元素中值最小或最大的。
这种堆分别称小顶(根)堆或大顶(根)堆
从图中可以看出,在一个堆中,根结点(称堆顶)具有最大值或最小值,而且堆中任何一个非叶子结点的左子树和右子树也是一个堆,根结点到任何一叶子结点的每条路径上的结点的值都是递减或递增的,即堆具有部分有序性。我们以大顶堆为例来讨论堆排序过程。小顶堆类似。
实现思路:
1、将初始序列建成堆,得到堆顶元素,最大元素
2、取出堆顶,将堆顶与堆的最后一个元素交换,堆最后一个元素更新
3、将剩余元素调整为堆,得到新的堆顶为第二大元素
4、重复步骤2,3知道最后堆为空,此时原序列有序
实现堆排序需解决两个问题:
(1) 怎样将待排序列构成一个初始堆;
(2) 输出堆顶元素后,怎样调整剩余的n-1个元素,使其重新成为一个新的堆。
完成这两项工作,要调用筛选算法。
筛选:就是将以结点i为根结点的子树调整为一个堆。
筛选的条件:结点i的左右子树必须已经是堆。
筛选算法的基本思想:
首先将与堆相应的完全二叉树根结点中的记录移出,该记录称为待调整记录。此时根结点相当于空结点。从空结点的左、右子中选出一个关键字较大的记录,如果该记录的关键字大于待调整记录的关键字,则将该记录上移至空结点中。此时,原来那个关键字较大的子结点相当于空结点。重复上述移动过程,直到空结点左、右孩子的关键字均小于待调整记录的关键字。此时,将待调整记录放入空结点即可。
如图:
以结点 15 为根节点的子树,左右孩子均已是堆,将根节点用tmp保存记录,15 与左右孩子中较大者比较,即与 54 比较,15小,把 54 置于堆顶位置,此时原 54 位置为空。
然后看原 54 位置是否有孩子结点,若有孩子结点,让 tmp 与 孩子最大值比较,小于孩子最大值 50 ,那么把 50 放置到空位置,此时原50 位置为空。
看原 50位置是否有孩子,发现没有孩子,把tmp值放到空位置,调整结束。
要进行整个序列的堆排序:需要我们将当前堆顶与堆尾记录交换,然后调用筛选算法重新调整,如此反复直至排序结束即可。
下面以序列 [ 21,25,49,25*,16,9] 为例进行展示:
代码实现:
def sift(li, low, high): # 调整为大顶堆
'''
:param li:列表
:param low: 堆的根节点位置
:param high: 堆的最后一个元素的位置
:return:
'''
i = low # i最开始指向根节点
j = 2 * i + 1 # j开始是左孩子
tmp = li[low] # 把堆顶存起来
while j <= high: # 只要j位置有数,表示有孩子结点
if j + 1 <= high and li[j + 1] > li[j]: # 如果有右孩子并且右孩子大于左孩子
j = j + 1 # j指向右孩子
if li[j] > tmp: # 孩子中较大的那个大于堆顶
li[i] = li[j] # 把大孩子置于根节点处
i = j # 往下看一层,让大孩子为根向下看有无孩子结点,没有就把tmp放到li[i]处
j = 2 * i + 1 # 此时li[i]已经放到其堆顶了,li[i]可理解为空,若无孩子,把tmp放置此处,完成交换
else: # tmp更大,把tmp放到i的位置上
li[i] = tmp # 把tmp放到当前某一级堆顶位置上
break
else:
li[i] = tmp # 把tmp放到大孩叶子节点上
def HeapSort(li):
n = len(li)
for i in range((n - 2) // 2, -1, -1): # 从下向上建堆
# i 表示建堆的时候调整的部分的根的下标
sift(li, i, n - 1) # 下->上调整
# 建堆完成了, 建造的是大顶堆
for i in range(n - 1, -1, -1): # 从列表最后一个元素开始向前与堆顶交换
# i 指向当前堆的最后一个元素
li[0], li[i] = li[i], li[0] # 将堆顶依次换到末尾,每次末尾减一,最后为升序排列
sift(li, 0, i - 1) # i-1是新的high,进行调整
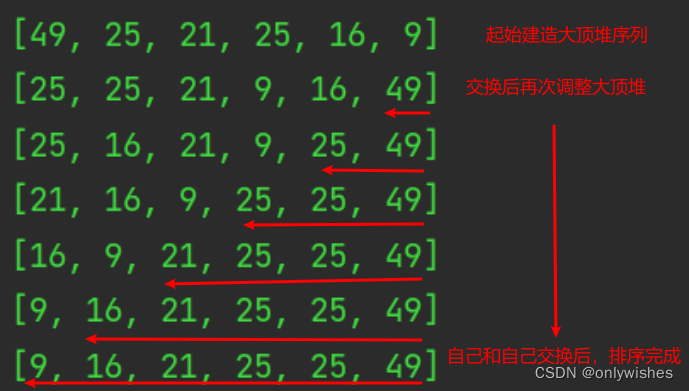
li = [49,25,21,25,16,9]
HeapSort(li)
print(li) # [9, 16, 21, 25, 25, 49]
排序过程如图: