LeetCode-105. 从前序与中序遍历序列构造二叉树【树数组哈希表分治二叉树】

news2024/10/9 20:25:27

LeetCode-105. 从前序与中序遍历序列构造二叉树【树数组哈希表分治二叉树】

题目描述：
解题思路一：暴力搜索
解题思路二：哈希查找
解题思路三：

题目描述：

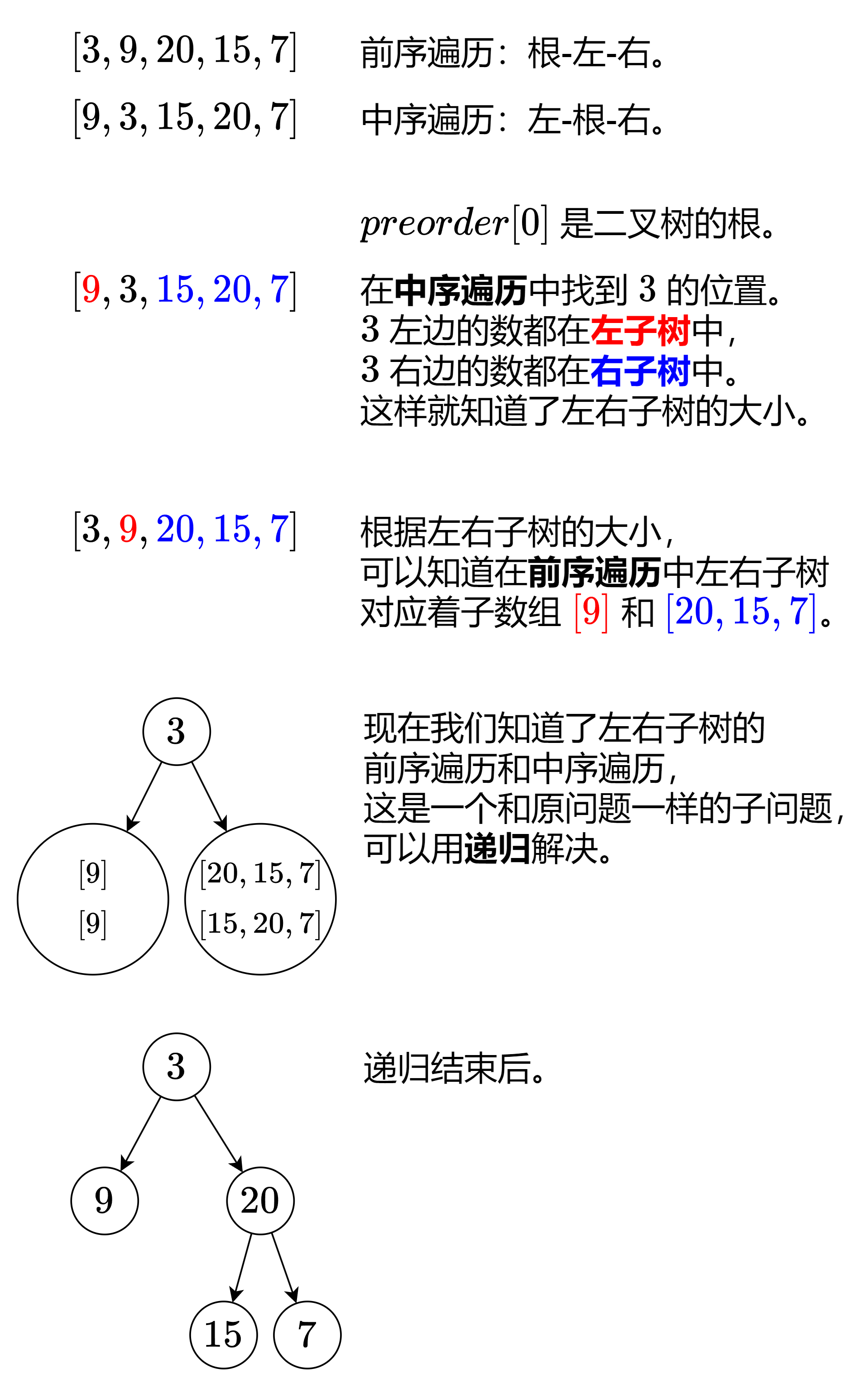
给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:
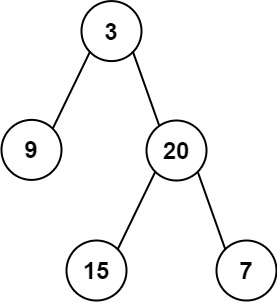
在这里插入图片描述
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均无重复元素
inorder 均出现在 preorder
preorder 保证为二叉树的前序遍历序列
inorder 保证为二叉树的中序遍历序列

解题思路一：暴力搜索

第一步：如果数组大小为零的话，说明是空节点了。

第二步：如果不为空，那么取后序数组最后一个元素作为节点元素。

第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点

第四步：切割中序数组，切成中序左数组和中序右数组（顺序别搞反了，一定是先切中序数组）

第五步：切割后序数组，切成后序左数组和后序右数组

第六步：递归处理左区间和右区间

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
        if not preorder:
            return None
        root_val = preorder[0]
        root = TreeNode(root_val)
        separator_idx = inorder.index(root_val)

        inorder_left = inorder[:separator_idx]
        inorder_right = inorder[separator_idx + 1:]

        preorder_left = preorder[1: 1 + len(inorder_left)]
        preorder_right = preorder[1 + len(inorder_left):]

        root.left = self.buildTree(preorder_left, inorder_left)
        root.right = self.buildTree(preorder_right, inorder_right)
        
        return root

时间复杂度：O(n²)
空间复杂度：O(n²)

解题思路二：哈希查找

在这里插入图片描述

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
        self.index = {x: i for i, x in enumerate(inorder)}
        if not preorder:
            return None
        root_val = preorder[0]
        root = TreeNode(root_val)
        # separator_idx = inorder.index(root_val)
        separator_idx = self.index[root_val]

        inorder_left = inorder[:separator_idx]
        inorder_right = inorder[separator_idx + 1:]

        preorder_left = preorder[1: 1 + len(inorder_left)]
        preorder_right = preorder[1 + len(inorder_left):]

        root.left = self.buildTree(preorder_left, inorder_left)
        root.right = self.buildTree(preorder_right, inorder_right)
        
        return root