Leetcode 93. 复原IP地址

讲解前：

这道题其实在做完切割回文串之后，学会了使用切割的方法来找到字符串的possible 子串之后，思路就会很快找到，细想一下其实无非也就是对given string然后进行切割，只是深度是固定的因为ip只能有四组数字组成，也就是四个sub string，然后呢我们就需要找到所有的possible组合，并且确保组合中每一个substring是符合规则的

并且当我们发现在for循环中，这一整个循环的加入的第一个path都是0开头的长度大于1的substring 的时候，就可以break 整个loop，但是按照我目前的思路，这道题还是有太多细节需要处理，所以我觉得先看题解

讲解后：
 

class Solution:
    def restoreIpAddresses(self, s: str) -> List[str]:
        res = []
        path = []

        # helper function to check if the current substring
        # is a valid ip address
        def is_valid(string):
            if not string:
                return False

            if string[0] == '0' and len(string) > 1:
                return False
            elif int(string) > 255:
                return False
            else:
                return True


        def backtracking(s, res, path, start_index, count):
            # base case
            # if we already added three substring to path
            # check the remaining one is valid or not
            print(path, '-', count)
            if count == 3:
                last_string = s[start_index:]
                if is_valid(last_string):
                    path.append(last_string)
                    res.append('.'.join(path[:]))
                    path.pop()
                    count = count - 1
                return

            
            # recursive case
            for i in range(start_index, len(s)):
                cur_string = s[start_index: i + 1]
                print(cur_string)

                
                if is_valid(cur_string):
                    path.append(cur_string)
                    count = count + 1
                    backtracking(s, res, path, i + 1, count)

                    path.pop()
                    count = count - 1

        backtracking(s, res, path, 0, 0)
        return res 

听完了卡哥的讲解之后发现其实这道题没有那么复杂，关键就在于当对substring是否是一个valid的id进行检查的时候，既然检查的条件会比较多比较繁琐，那么就直接封装成一个函数就好了，然后呢思路就和其他切割字符串的题没区别了，就是检查每一个substring，如果符合要求，就在基础上继续递归找下一个符合条件的，唯一比较特殊的是，在base case中，这里我们只有三条切割线，最后第四个substring需要我们在找完三次之后直接取剩余的string作为第四个，所以在base case中我们还需要再对path进行一次添加，同时这里要注意，这一次添加也需要做回溯操作也就是对path进行pop以及减少count的值

---

Leetcode 78. 子集

讲解前：

这道题的思路其实很简单，题目中需要求的子集其实我们同样把树形结构画出来之后就发现，只不过是在递归的过程中把path的值收集一下，因为如果我们没有特定的组合的要求，那么每一个path在递归的过程中就是一个组合，并且通过我们对i的递增，还可以保证不会重复

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        res = []
        res.append([])
        path = []

        def backtracking(nums, res, path, start_index):

            for i in range(start_index, len(nums)):
                path.append(nums[i])
                res.append(path[:])

                backtracking(nums, res, path, i + 1)

                path.pop()
        
        backtracking(nums, res, path, 0)
        return res 

讲解后：

看了卡哥的讲解发现我其实没必要在for循环里面直接加入res，并且在一开始把空列表先加进去，因为我一开始害怕我们进入函数之后，在重新从2开始递归之前还会出现一次path为空的情况，包括3也是，但其实并不会，在pop了之后，我们还是继续循环并且把数字加入到path之后才会再递归，所以把加入res的代码写在backtracking的第一行就可以了

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        res = []
        path = []

        def backtracking(nums, res, path, start_index):
            # every recursive call, add the current path to res
            res.append(path[:])
            
            for i in range(start_index, len(nums)):
                path.append(nums[i])

                backtracking(nums, res, path, i + 1)

                path.pop()
        
        backtracking(nums, res, path, 0)
        return res 

---

Leetcode 90. 子集II

讲解前：

这道题其实就是之前组合问题的变种，关键就在于去重，就如下图中所示的

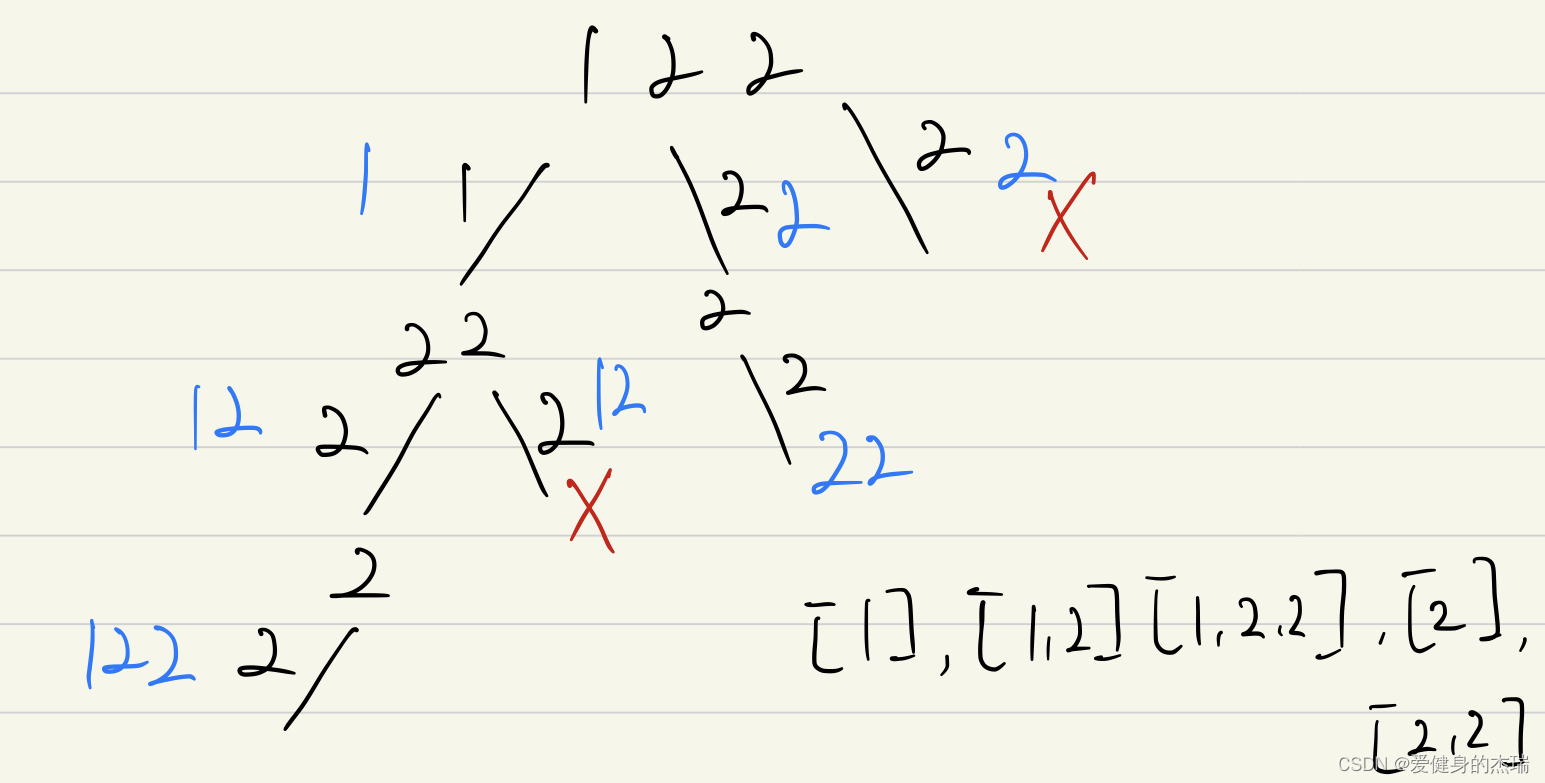
[1, 2] 和 [2] 会反复出现，但是我们不能重复取，这里其实思路就是如果我们是在纵向搜索，也就是说是在继续增加数字然后扩大子集，那么就没关系，但是如果是横向的代表集合由前一个数字开头的已经全部找完了，那么如果我们再从这里开始并且当前这个数字和之前的那个一样，那么我们一定会再end up with the same set，那么这里其实还有个更简单的方法如果我们当前的index和上一位相等并且是在i比startindex大的情况下，因为这时候证明我们是在纵向递归，并且要记得这种方法的前提是我们要先把nums变成递增顺序才可以，这样两个相同的数字才会next to each other

class Solution:
    def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
        res = []
        path = []
        nums.sort()

        def backtracking(nums, res, path, start_index):
            # add the current path to res each recursion
            res.append(path[:])

            for i in range(start_index, len(nums)):
                if i > 0 and nums[i] == nums[i - 1] and i > start_index:
                    continue
                
                path.append(nums[i])
                backtracking(nums, res, path, i + 1)
                path.pop()
        
        backtracking(nums, res, path, 0)
        return res 

讲解后：

卡哥的解法就和之前讲解组合去重问题时候一样，利用了一个used数组，思路依然很清晰，但是这里我的写法更加简便一点，虽然需要在理解了used数组的解法之上去想明白才能看懂

这里是文字解法中利用used数组的解法

class Solution:
    def subsetsWithDup(self, nums):
        result = []
        path = []
        used = [False] * len(nums)
        nums.sort()  # 去重需要排序
        self.backtracking(nums, 0, used, path, result)
        return result

    def backtracking(self, nums, startIndex, used, path, result):
        result.append(path[:])  # 收集子集
        for i in range(startIndex, len(nums)):
            # used[i - 1] == True，说明同一树枝 nums[i - 1] 使用过
            # used[i - 1] == False，说明同一树层 nums[i - 1] 使用过
            # 而我们要对同一树层使用过的元素进行跳过
            if i > 0 and nums[i] == nums[i - 1] and not used[i - 1]:
                continue
            path.append(nums[i])
            used[i] = True
            self.backtracking(nums, i + 1, used, path, result)
            used[i] = False
            path.pop()