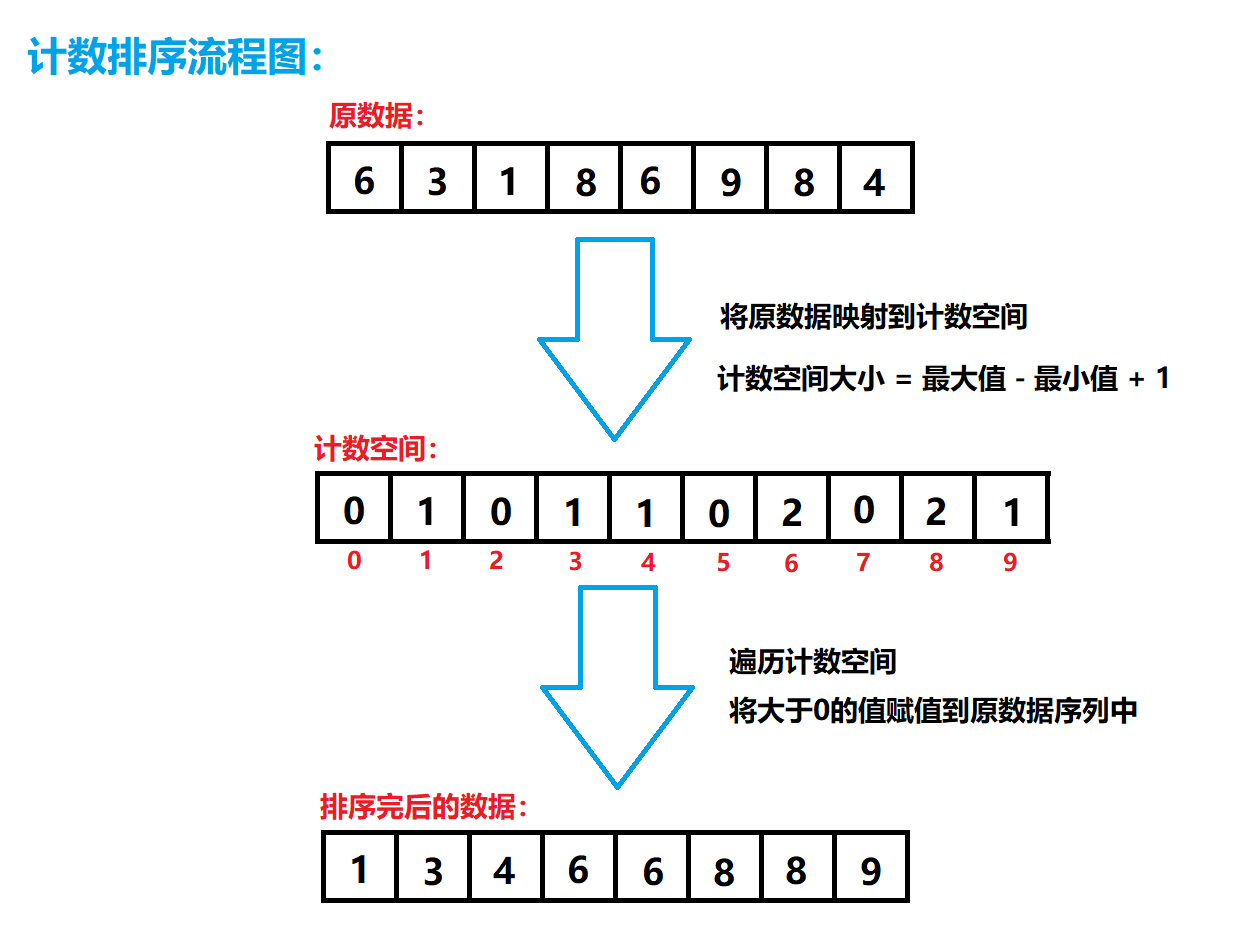
解决之路= =

题目描述

测试案例（部分）

第一次

和昨天的题目有点类似，昨天是找重复，今天是找不重复。那直接按昨天第二次思路来写这次的代码。

class Solution(object):
    def singleNumber(self, nums):
        nums.sort()
        for i in range(len(nums) - 1):
            if nums[i] != nums[i+1]:
                return nums[i]

测试正确，提交，报错了。

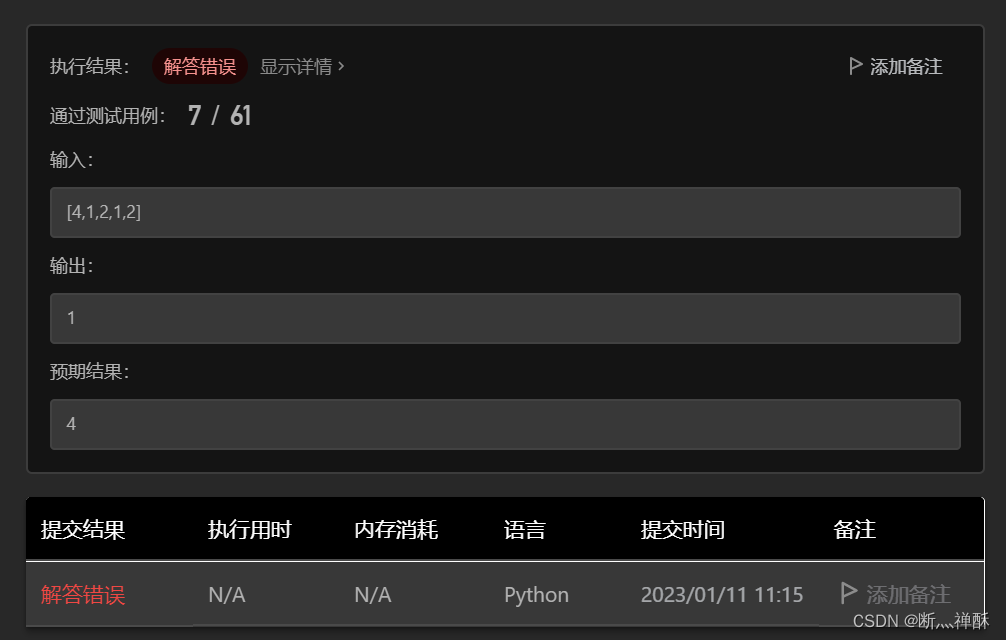
未通过案例是[4,1,2,1,2]，排序后是[1,1,2,2,4]，判断到下标1的1和下标2的2不相等，所以输出了1，导致了错误。

第二次

想想如果避免这个错误，得想个法子跳过一些下标。想了想，方案不可行，太复杂了，设计如何跳过两个重复的元素倒还好，如果三个重复、或者其他情况，可能就不适用了。

那先昨天第一次的代码能跑通嘛？想了想，也跑不通理由还是一样。想想其他思路。

做数学题从小就教，一直想不到办法就重新看看题。重新看了下题：

除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

也就是说，只会出现重复两次的情况和不重复的情况两种，没有其他情况。那么这么说，我们之前的思路是可以往下完善的。不过，为了避免第一次的错误，我们得跳下标，不过，删除相同元素也是间接的跳下标。

class Solution(object):
    def singleNumber(self, nums):
        index = 0
        nums.sort()
        try :
            while nums[index] == nums[index + 1]:
                nums.pop(index)
                nums.pop(index)
            return nums[0]
        except IndexError:
            return nums[0]

测试正确，提交，成功了，不过耗时较大。

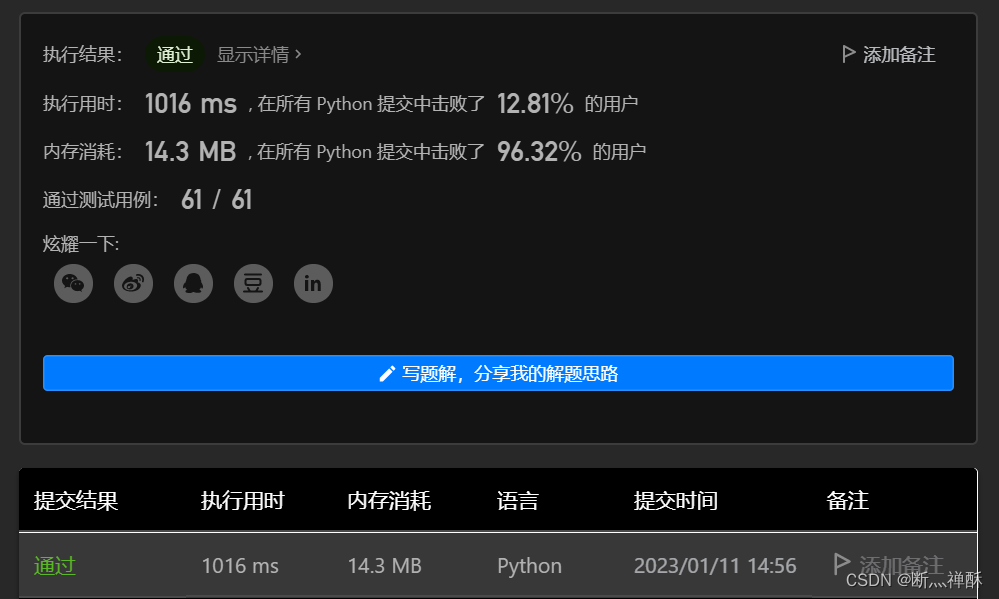
第三次

woc，评论区很多都在说用“异或”运算解决。之前学计组和数字逻辑，了解过异或运算，这次还是第一次用异或运算来解决实际问题。

异或运算的数学符号：⊕，英文符号为：XOR，在python中和and、or一样，xor也是一种逻辑运算
a⊕b = (¬a ∧ b) ∨ (a ∧¬b)
如果a、b两个值不相同，则异或结果为1。如果a、b两个值相同，异或结果为0。

关于异或运算的运算律

1. 交换律：a ^ b ^ c <=> a ^ c ^ b
2. 任何数于0异或为任何数 0 ^ n => n
3. 相同的数异或为0: n ^ n => 0

以[2,2,1]举例，循环到最后就是这个2^2^1的结果，按照上面的三个运算律，就可以推出答案：
2^2^1=0^1=1，就是最后的没有重复的元素！

再来一个长的，[4,1,2,1,2]，经过循环，最后得到4^1^2^1^2，根据交换律，=1^1^2^2^4=0^0^4=4。

这样，就可以理解了，只要列表中有两两重复的元素，那他们两两消除，像消消乐一样，最后剩下的，就是那个唯一的不重复的元素。

杂谈

偶然往下看了看评论区，看到一个挺有意思的思路的。如果有两个重复的元素，那么他们加起来就可以被2整除。这样就可以去判断是否有两个重复元素的情况了。

不过，这个解决方案不符合题目要求，评论区有人指出该算法的时间复杂度为O(nlog₂n)，不是线性的时间复杂度。

但这个方法思路也挺好的，也算学到了一个思路。

附件