Search-based Path Planning Methods
Path Finding Problem
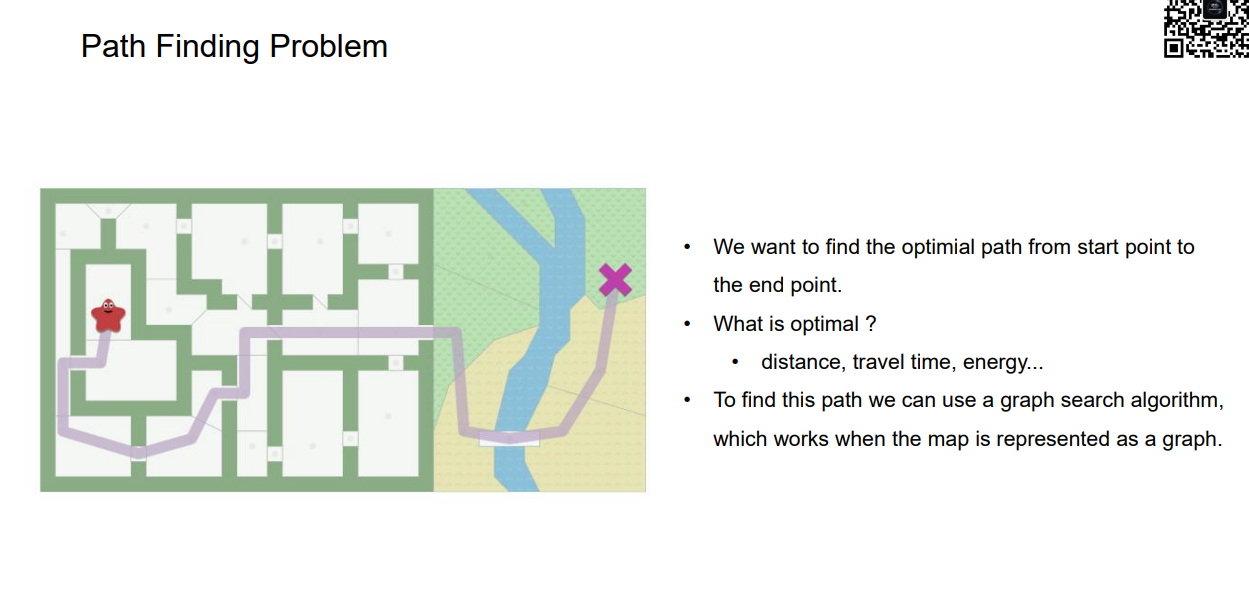
一般来说指标有距离,耗费时间,能量,或者多目标。
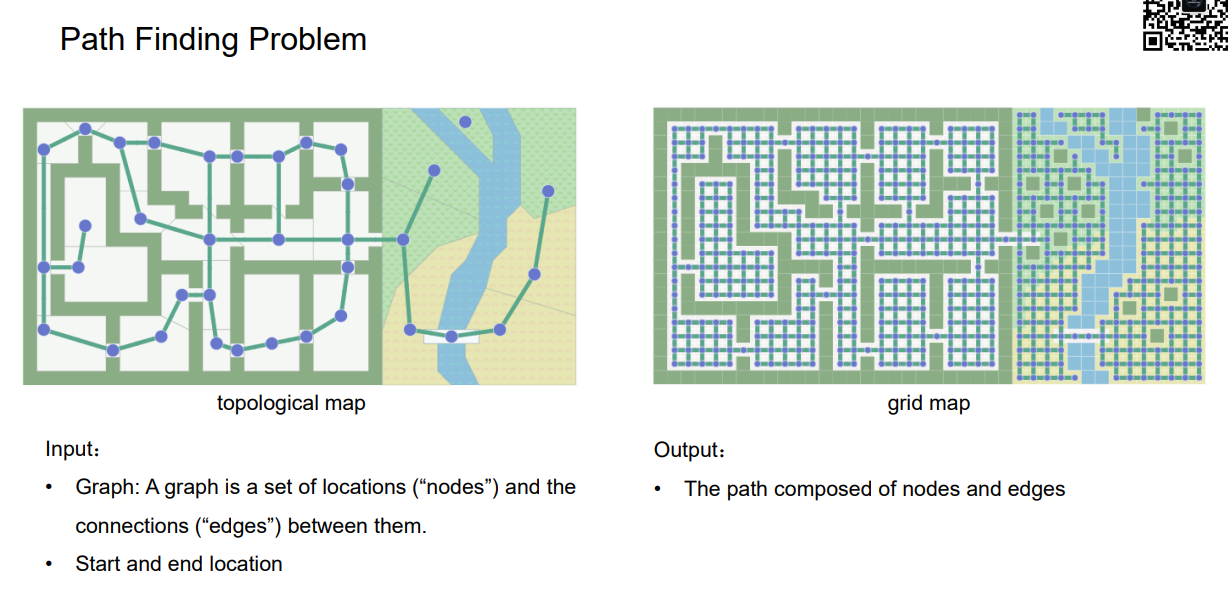
左图是拓扑地图,蓝色的点就是顶点,绿色的线是连接关系。最后得到的是一个从哪里走的一个最优,并非精细解。
右图是栅格地图,这个搜索出来的是在相对分辨率比较高的情况下的最优路径。
路径搜索问题的输入输出是什么:
输入:给出一副由节点和边构成的图论上的图,起点和终点
输出:返回一条由节点和边组成的path
Graph Basic
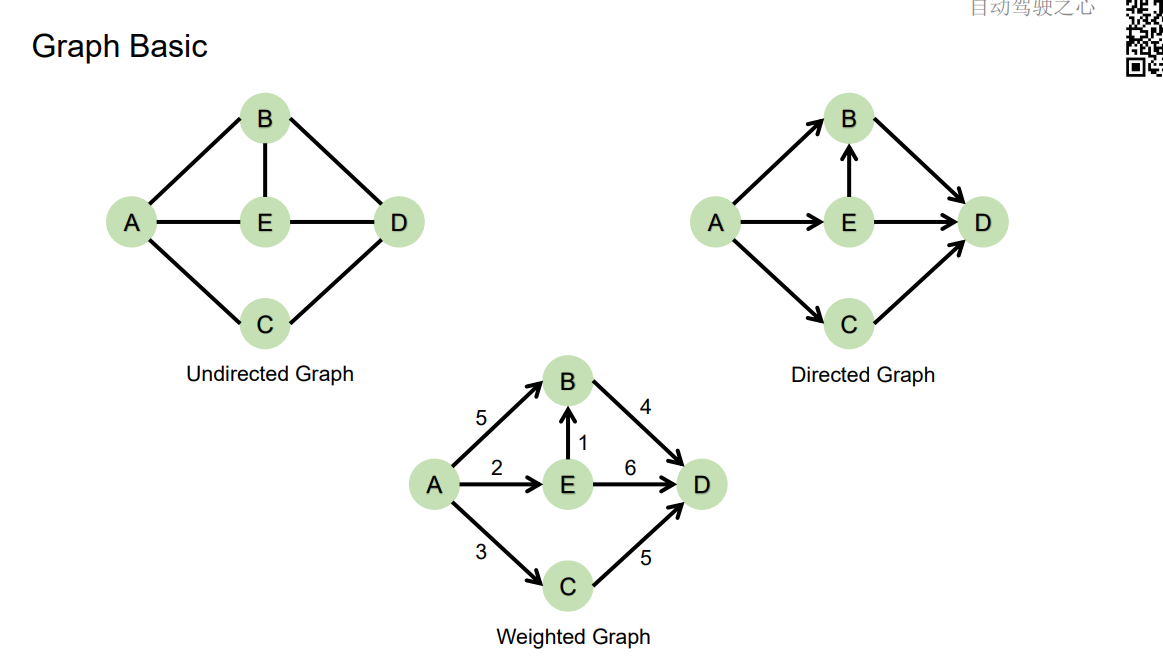
无向图(可以从节点A-B,也可以B-A)、有向图(可以从A-B,但是不可以B-A)、带权重的图(有了每条边的代价,来定义哪条路最优)
Some ways to Construct Graph
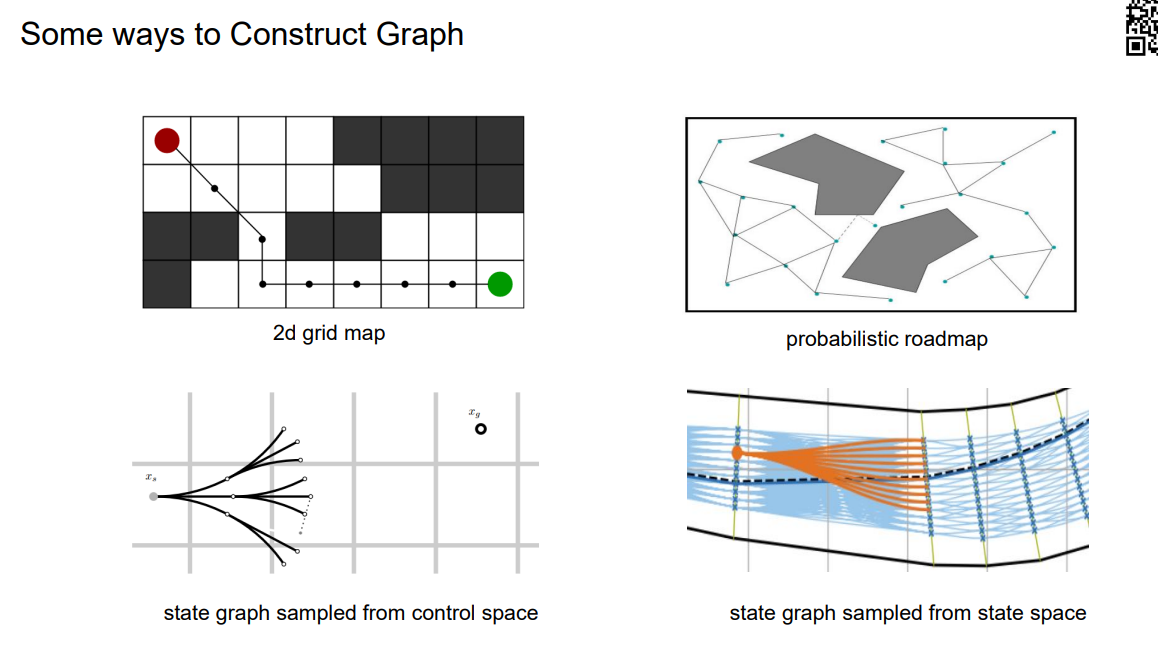
基于实现的效果来定制图。
栅格地图:每个顶点就描述栅格中心世界坐标系下的坐标,有天然的连接关系,与周围八个节点天生连接。
概率路图:通过采样得到的,采样顶点,通过规则,选择边。
state graph sampled from control space :运动基元构成的,给定转角和速度,通过积分的方式得到一小段轨迹。
state graph sampled from state space:给定起点终止顶点,根据逆动力学来构造运动基元。
Graph Traversal Algorithm
BFS
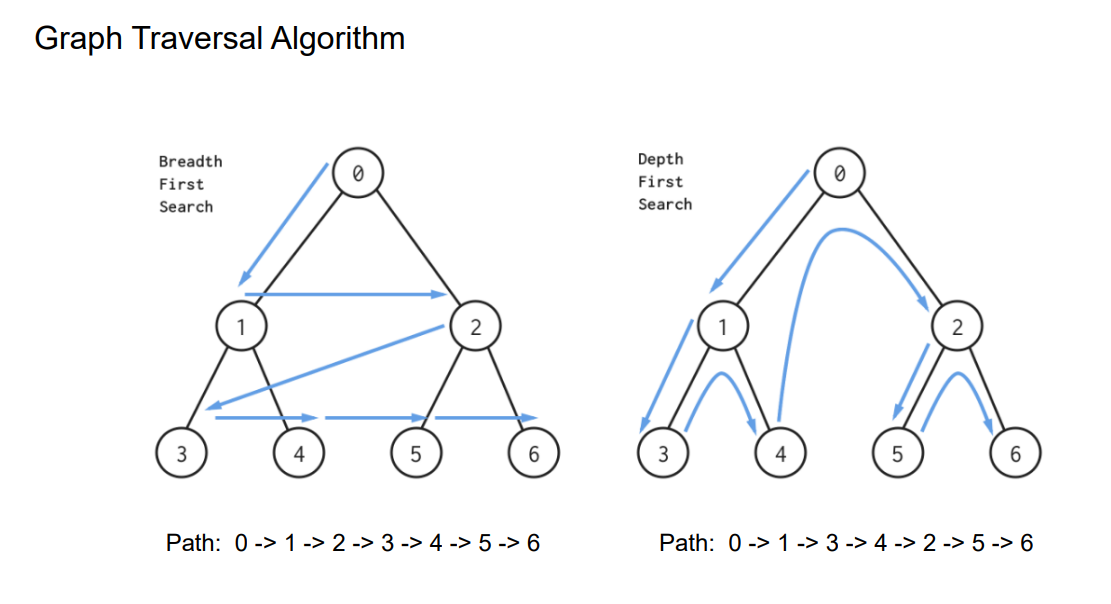


队列,先进先出,层序遍历。
算法输入是:一幅图,起始节点、终止节点。
输出是:从终点回溯到起点的最短路径。
步骤:先定义队列Q,然后把起始节点加入到队列中,然后把起始节点标记成已访问。
主循环:终止条件:队列Q没有节点,也就是所有节点都访问过了,另外一个条件式访问的节点是终点。
弹出队列的第一个节点,依次访问节点周围的邻居节点,如果节点没有访问过,就把节点加入到队尾中,并且把父节点标记成当前节点,并且把这个节点标记成已访问的状态。不断循环,就可以遍历到所有节点,如果存在可行路径,一定能找到。
BFS Search Process
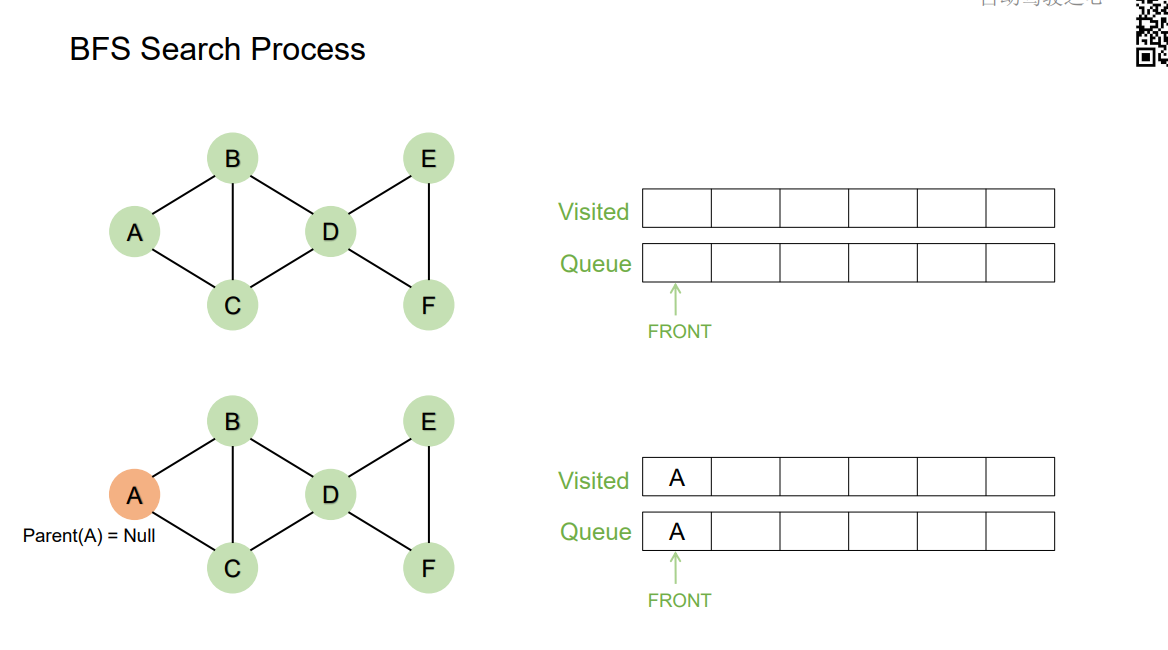
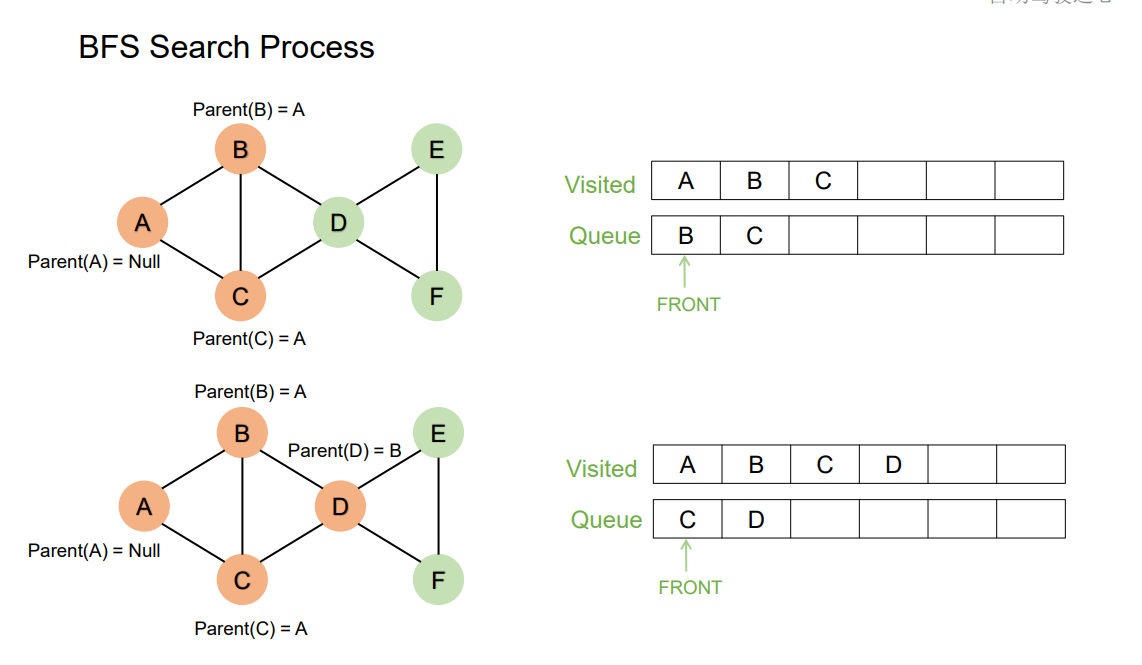
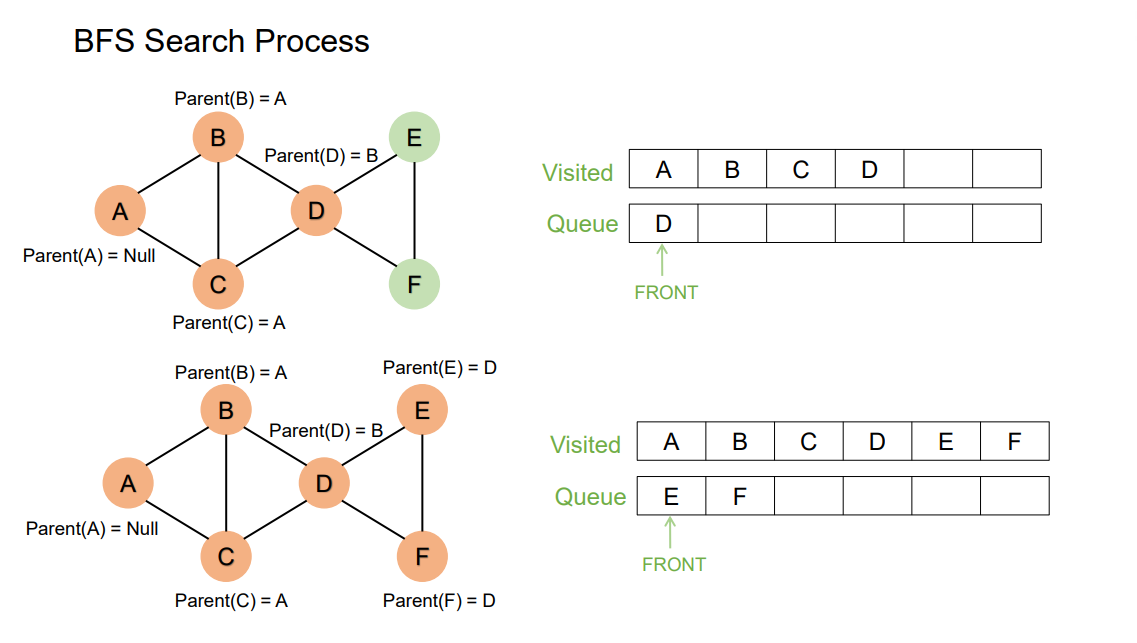
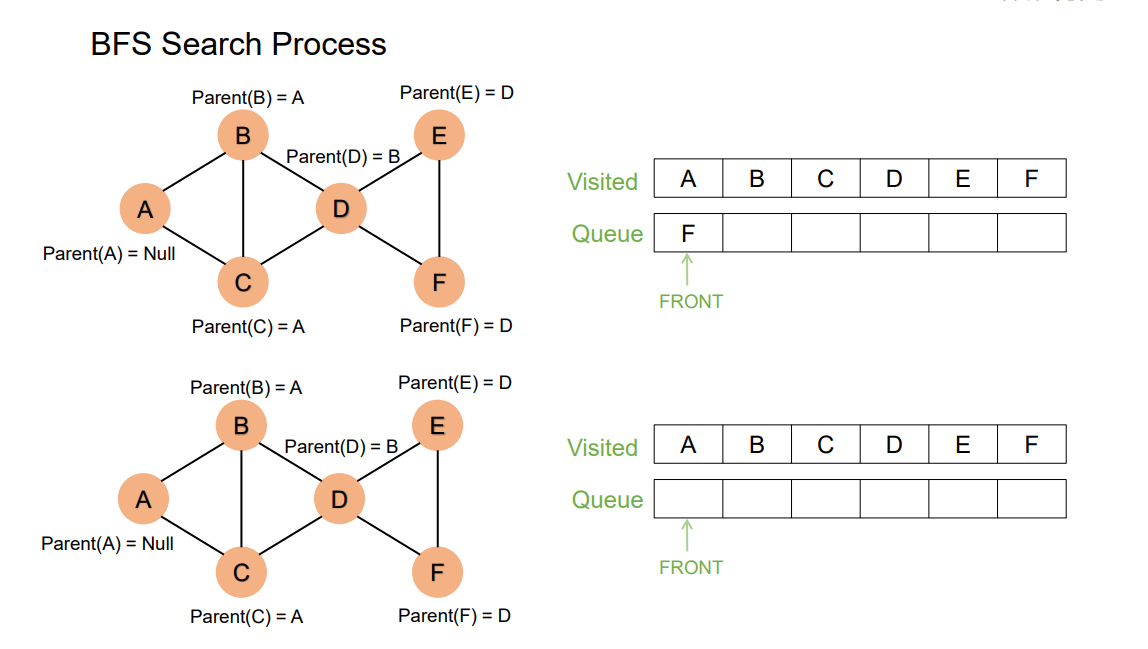
Summary

1、会相同的探索所有的方向
2、如果所有边的权重为1,那么BFS搜索出来的路径就是cost最优的路径。
Dijkstra

维护了一个新的变量g(n),g(n)是从起始节点到当前节点n累计的代价,访问的是在openset中累计代价最小的那个节点去访问,采用贪心的思想。
Priority queue

优先级队列,为容器赋予优先级。
Algorithm Dijkstra

输入:有个图,有个起点的节点和终点节点
输出:一条从终点节点向起点节点回溯得到的最短路径
Dijkstra Search Process
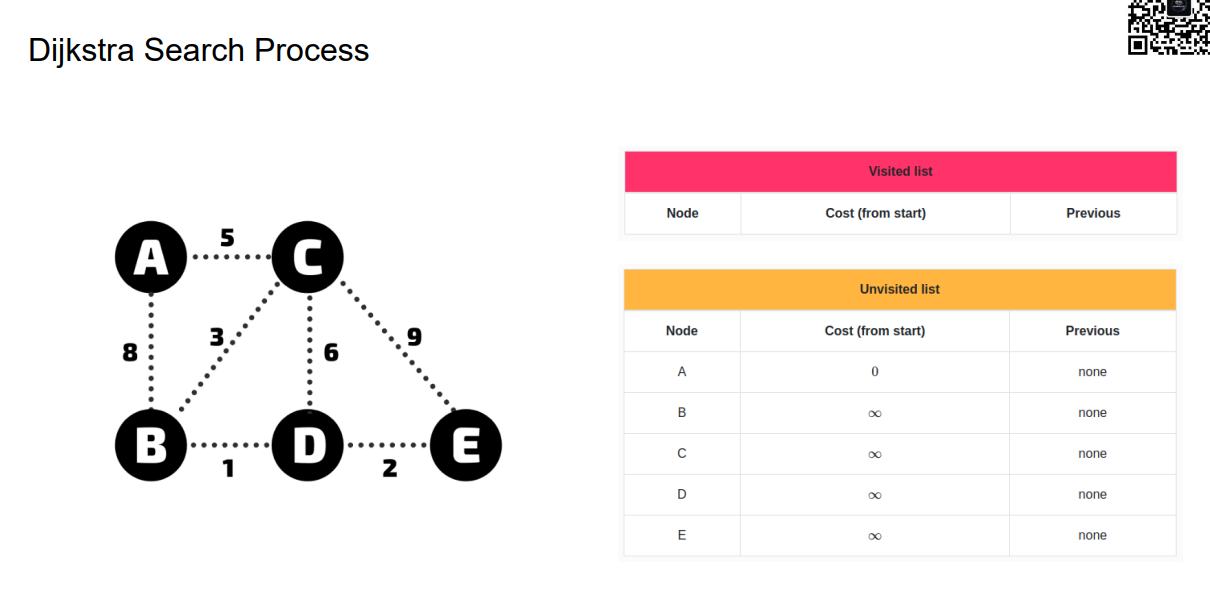
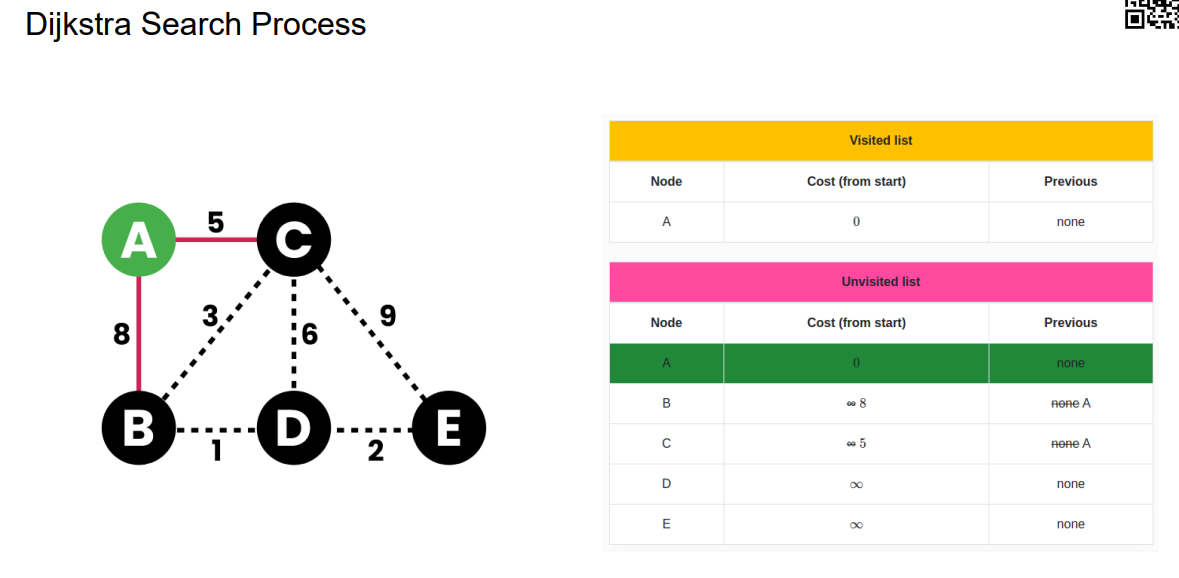



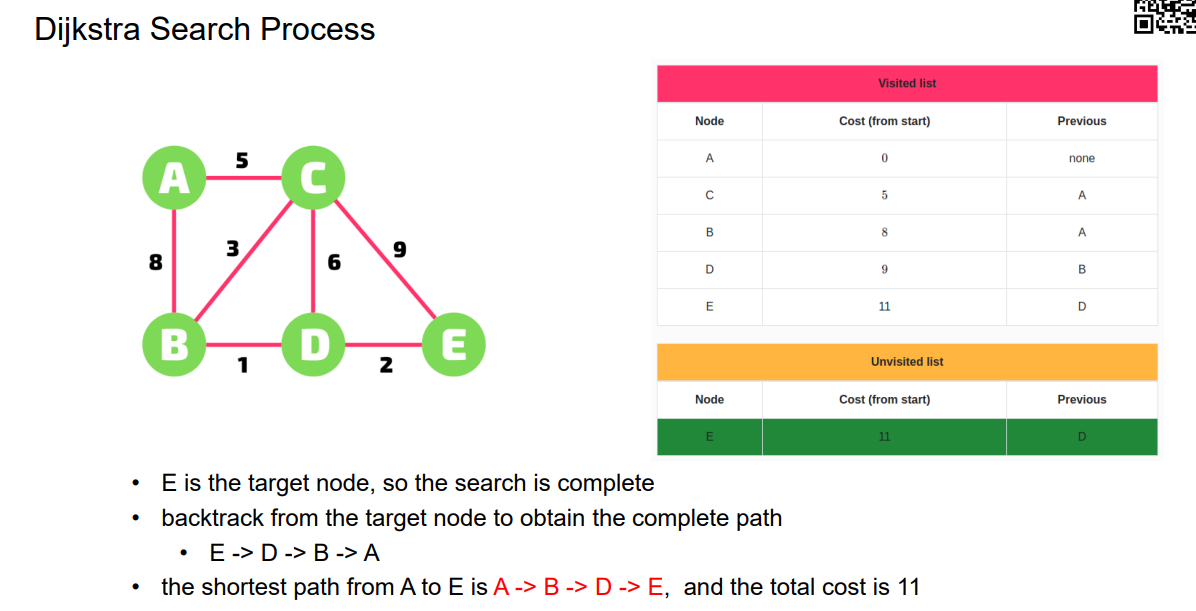
Summary

优点:
1、可以获得到起点到任何节点的最短路径
2、满足最优性
缺点:
1、无启发函数
A* Algorithm
Core ideas

Dijkstra在搜索的过程中是不知道终点信息的,搜索效率不高。A*算法设计一个到目标点的启发式函数,此时用f来描述每个节点的cost(f = g + h)。
这里可以简单的画个图,如图所示,Dijkstra会浪费一部分计算资源去扩展与终点较远的节点,对于A*算法会更有目的性一些。
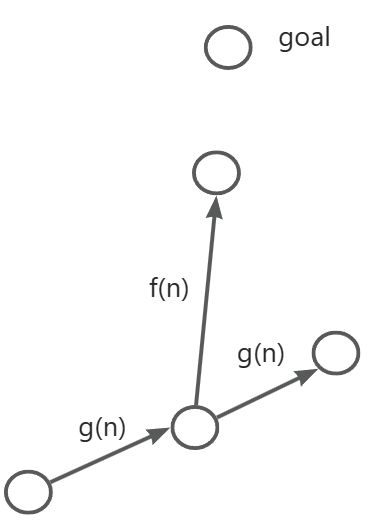
A* Search Process

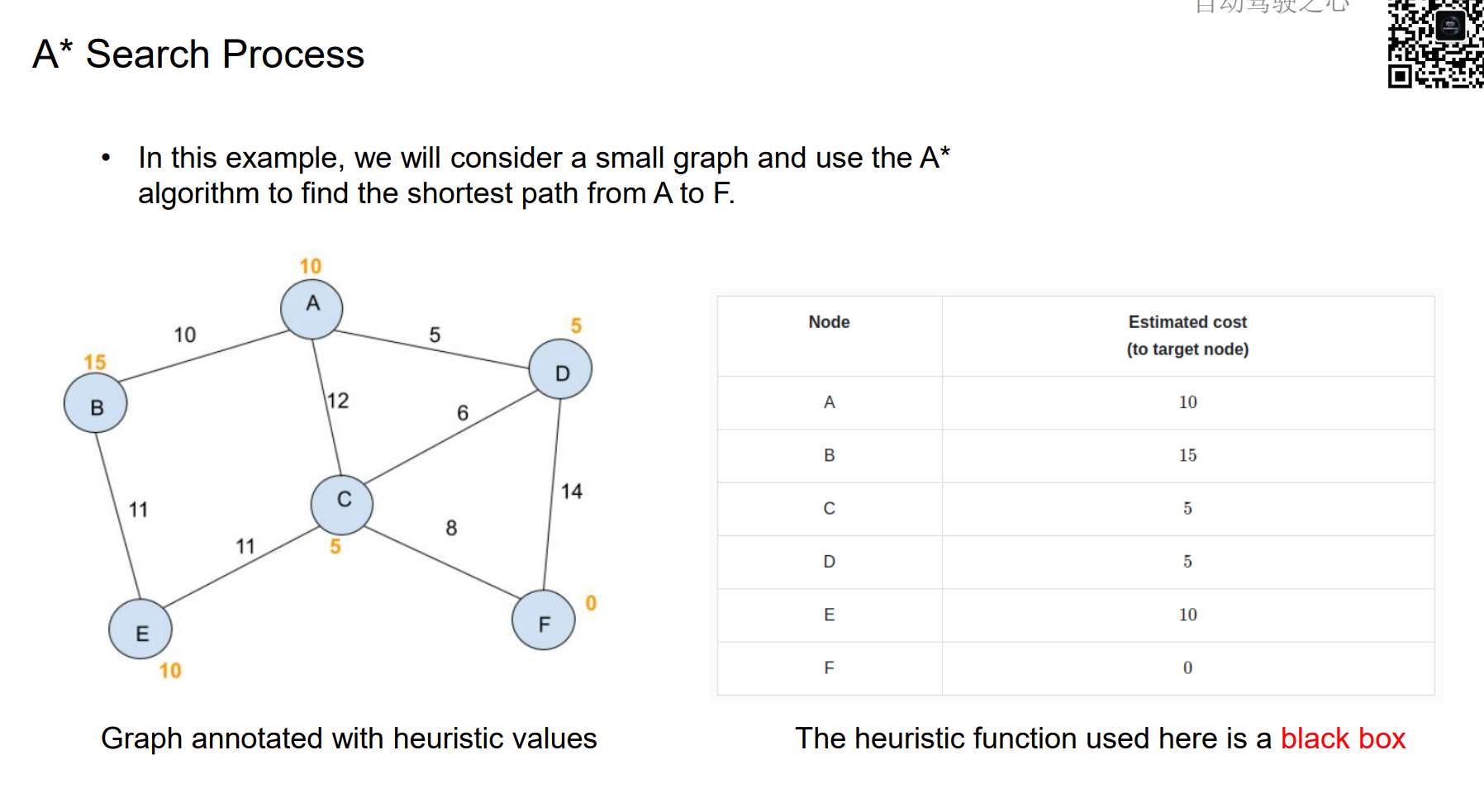

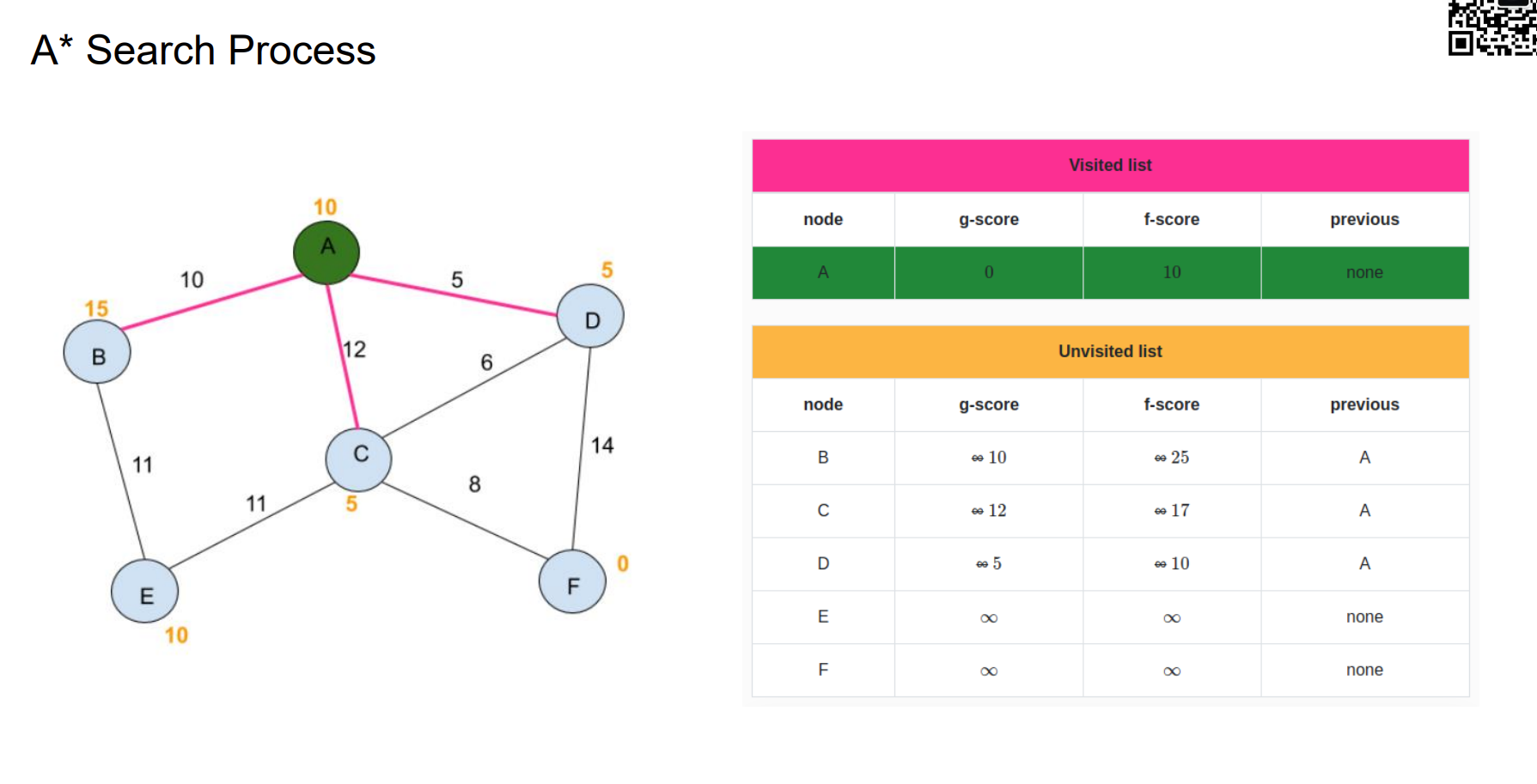
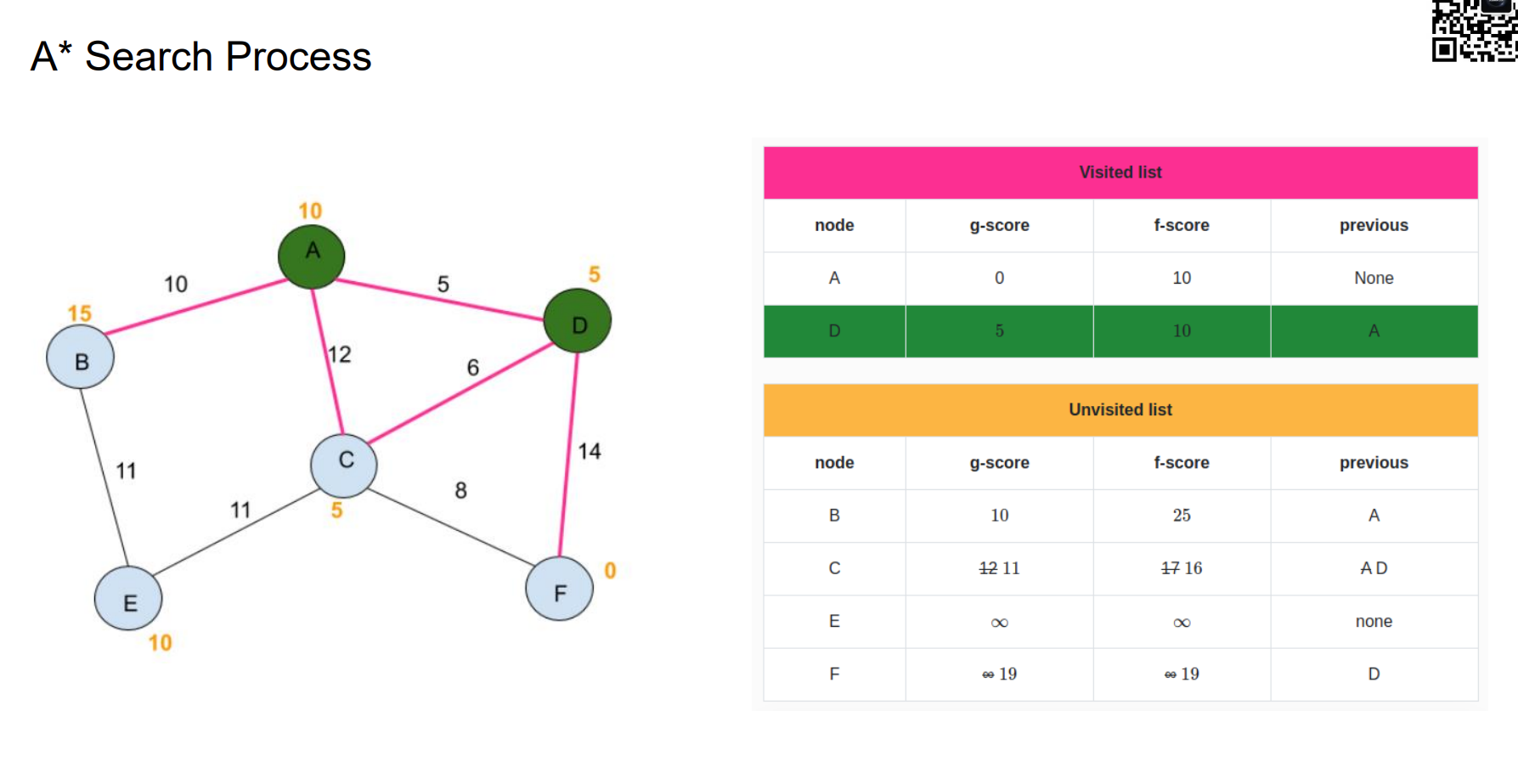
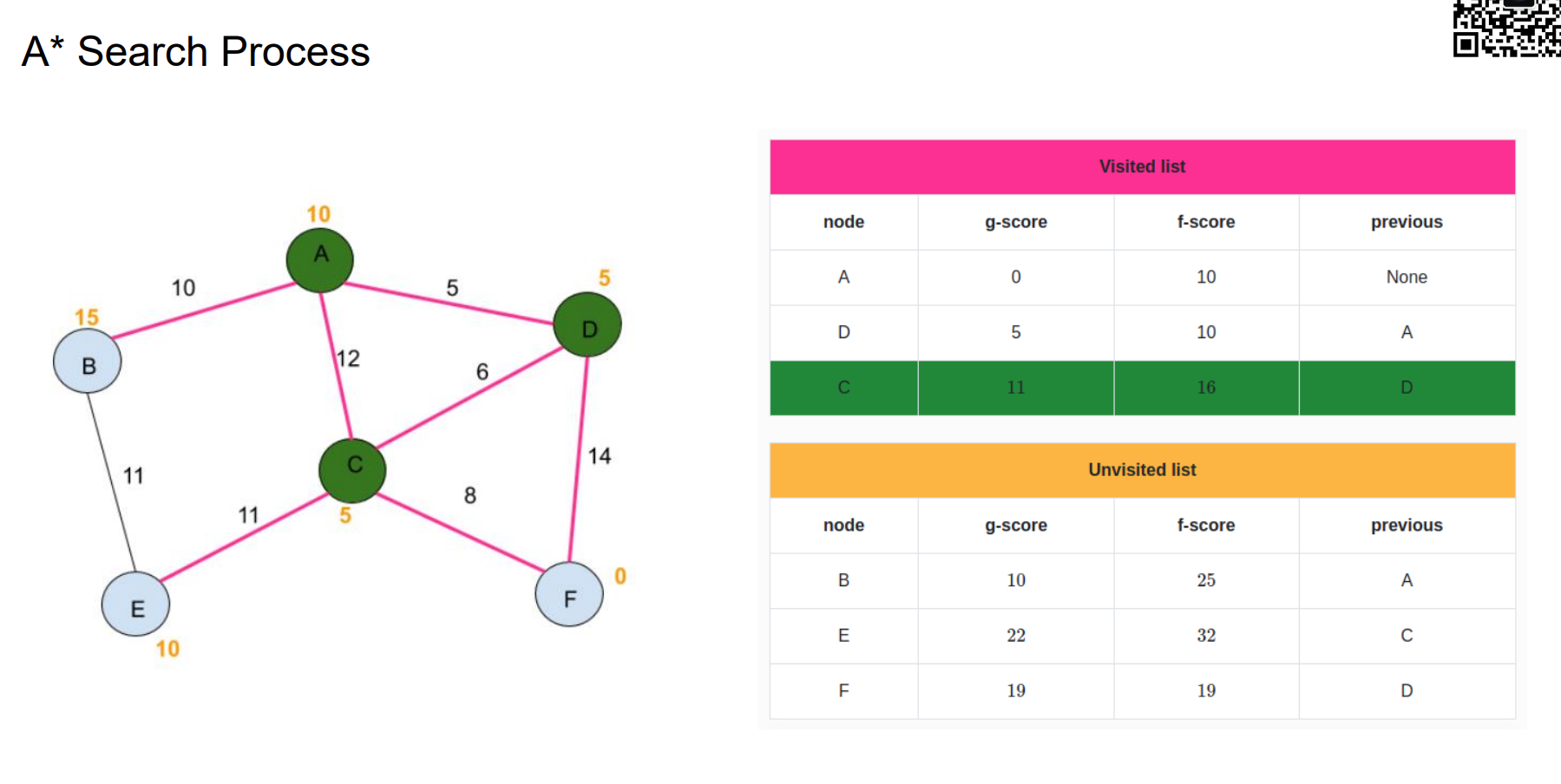
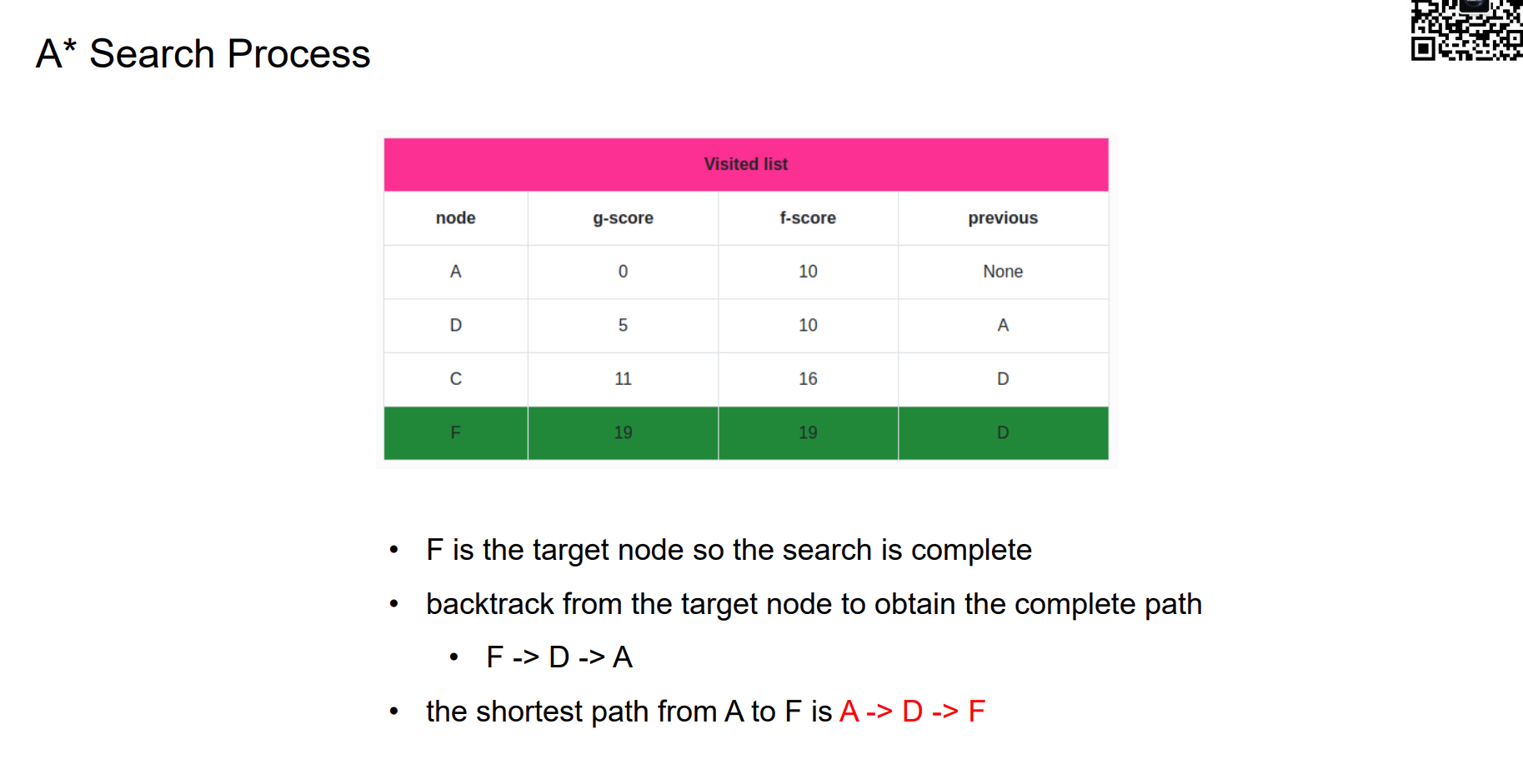
Heuristic Function Design

启发式函数的设计和具体任务有关系,如果说搜索问题的最优指标和距离有关系的话,那么可以用下面这几种距离来定义启发式函数。

Euclidian distance其实对应的是一个二范数,在几何上就是直线距离。
Manhattan distance在数学上就是一范数。
Great circle distance描述的是球面上两点的最短路径,对应于是弧长的概念。
Optimality

如何设计启发式函数能保证A*算法的最优性:heuristic function不能高于costs。也就是估计值需要小于真实值。如果满足这一点,那么A*算法一定能找到最优解的,且比Dijkstra快。
What’s Wrong with Overestimated Heuristics?
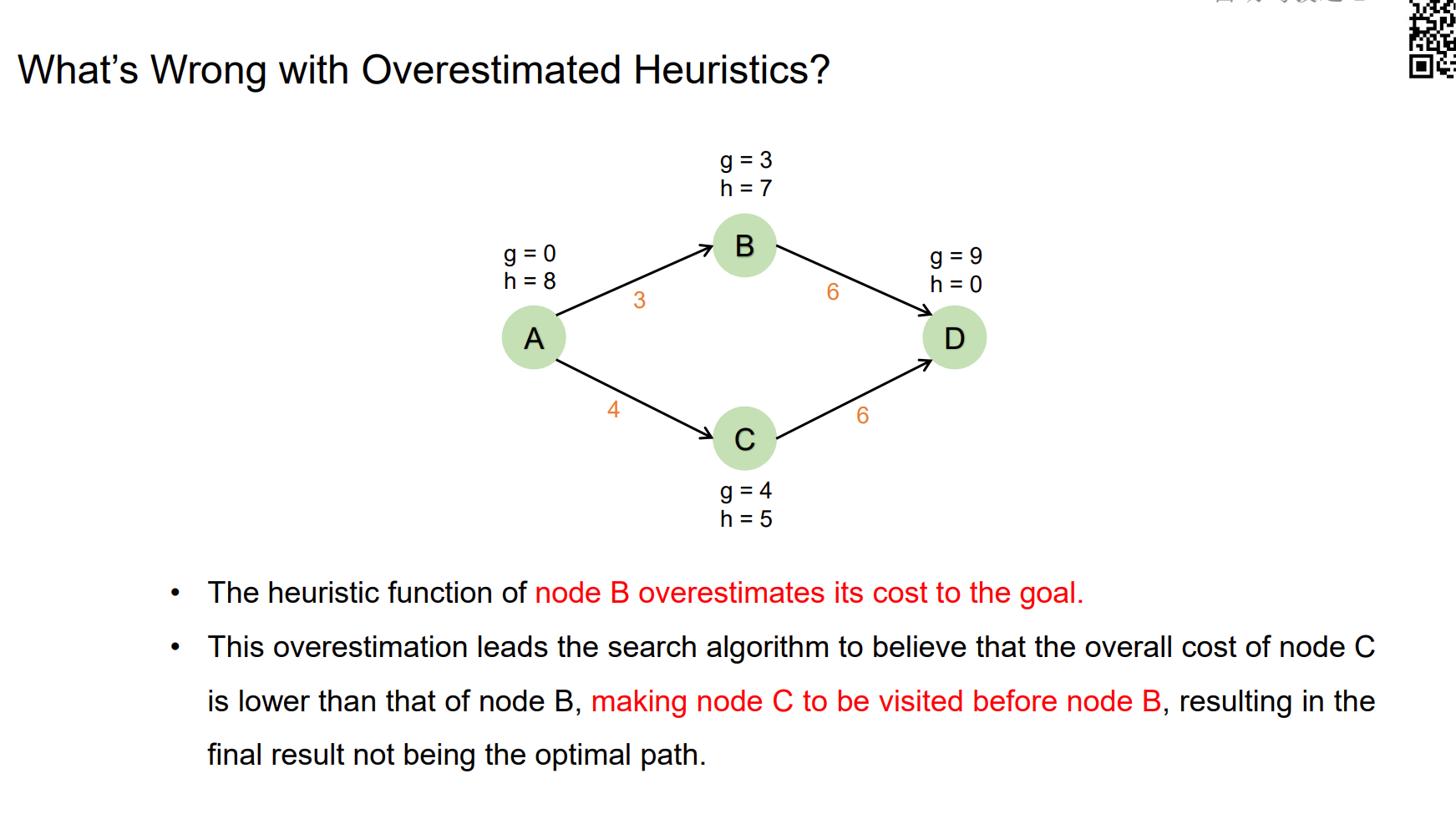
对于上图而言,根据A*的逻辑,选择ACD这个路径,但是真实情况是ABD的代价最小,出现这样的计算错误是由于B的h值大于真实的cost。
Heuristic Function Design in Gridmap
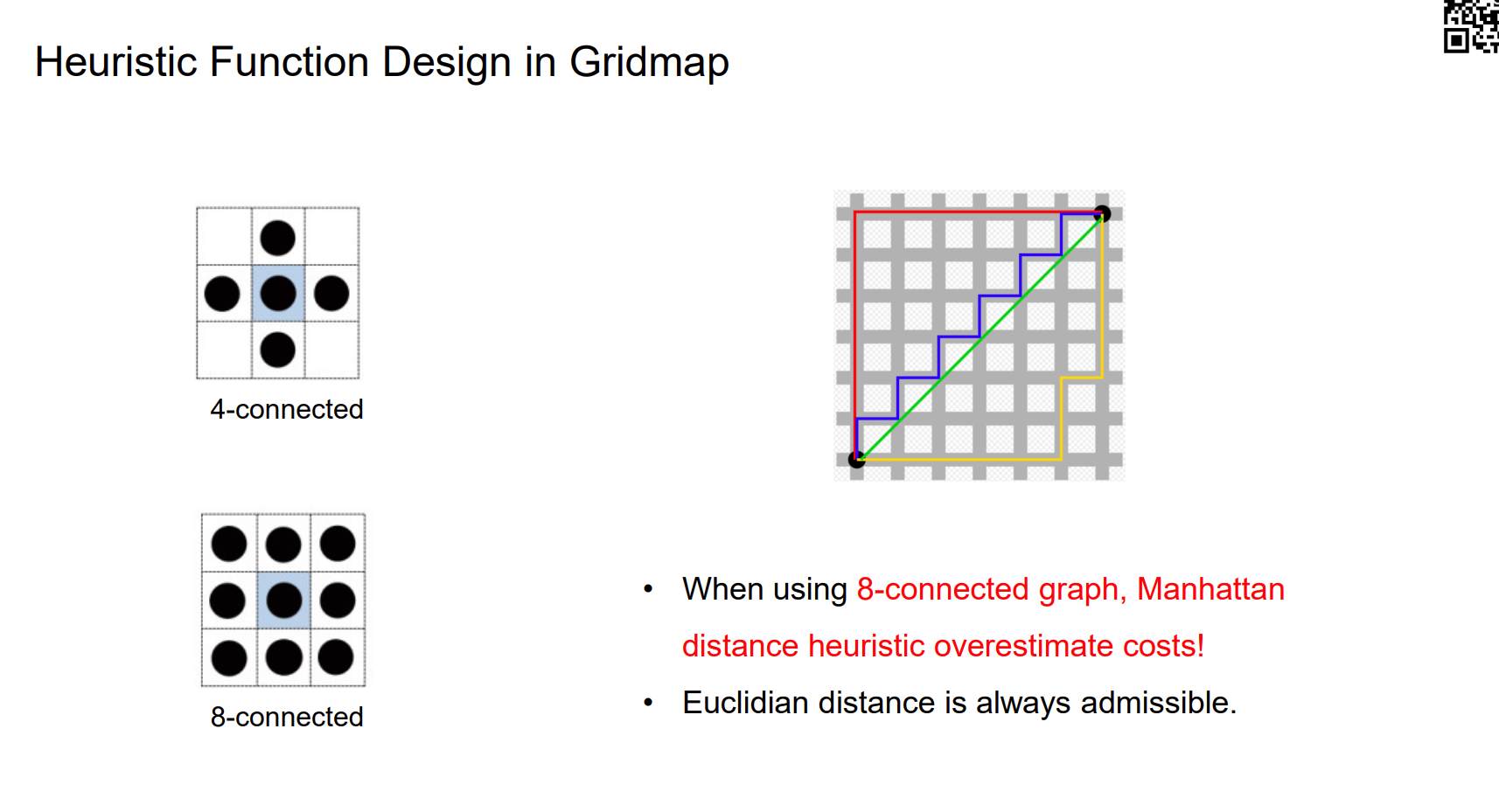
对于八连通的形式,用Manhattan distance会高估cost,可能导致找不到最优解。欧式距离可以使用。
Efficiency and Accuracy
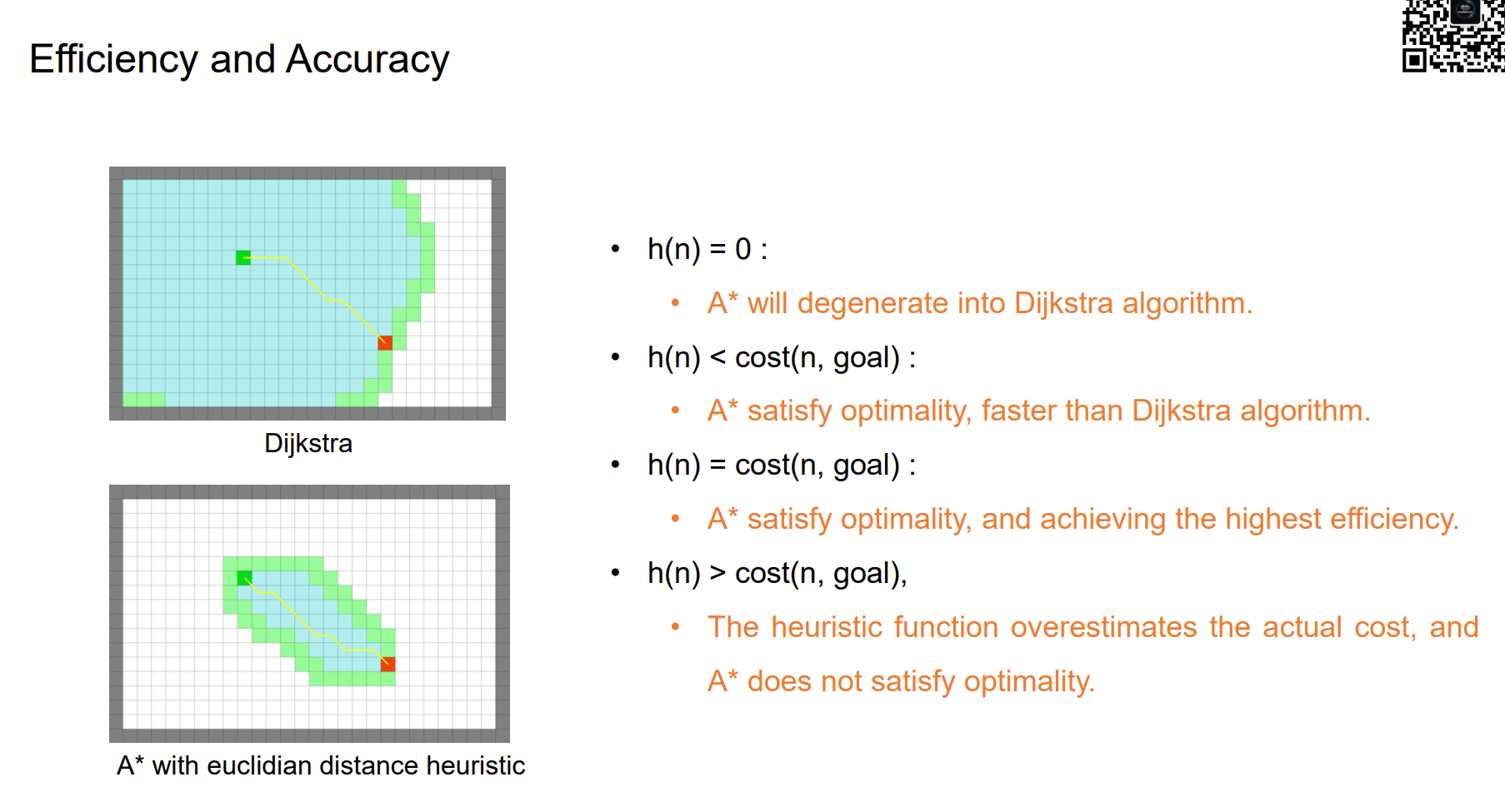
Summary

Dynamic Programming
What is Dynamic Programming

对于一个动态规划的问题,具有
1、有一个最优的子结构
2、对于所有的子问题,有很多是重复的。(这里相当于,如果一个子问题之前计算过了,那么就将结果保存起来,后续可以通过查表的形式,不用重复计算)
Tiny Example of Dynamic Programming

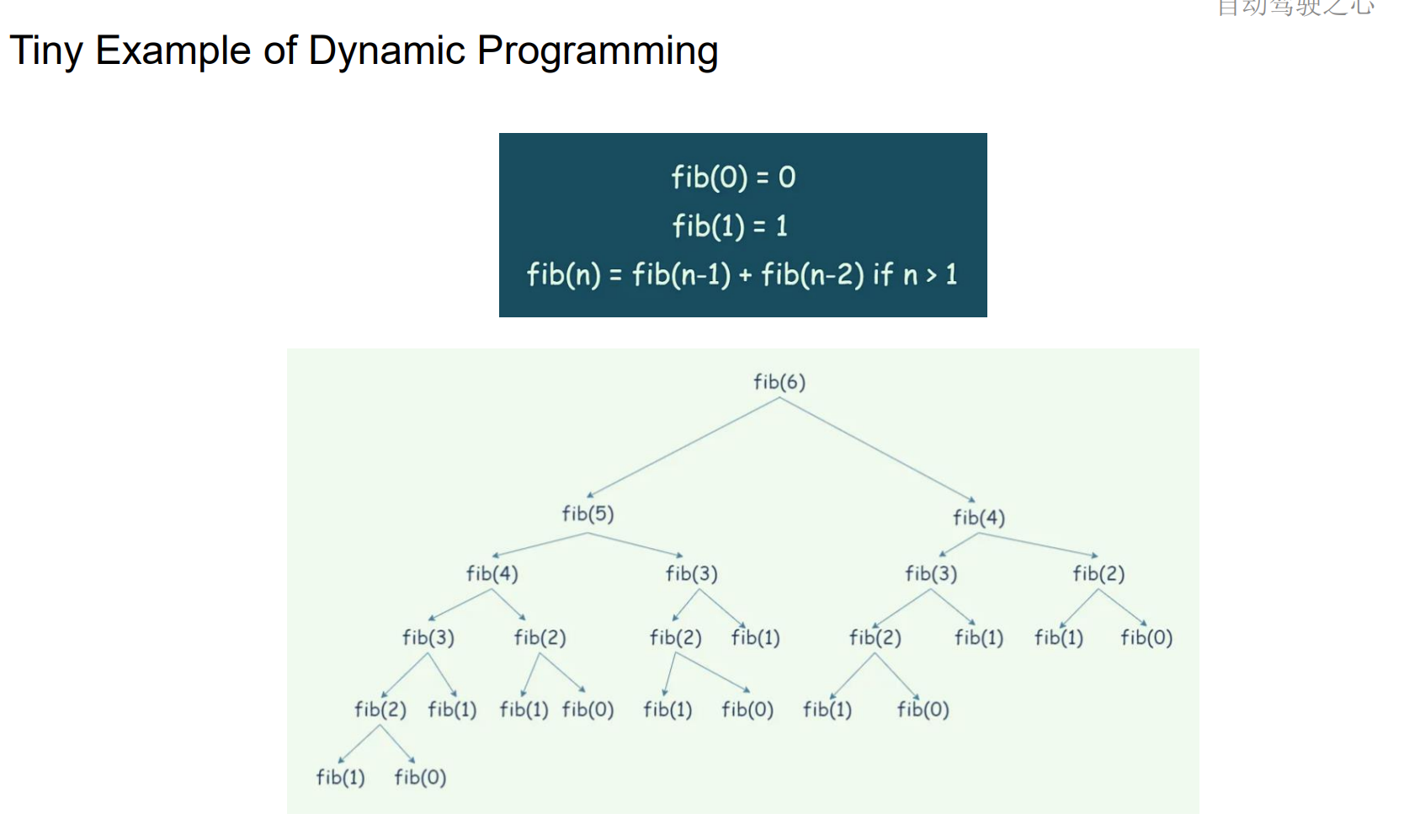
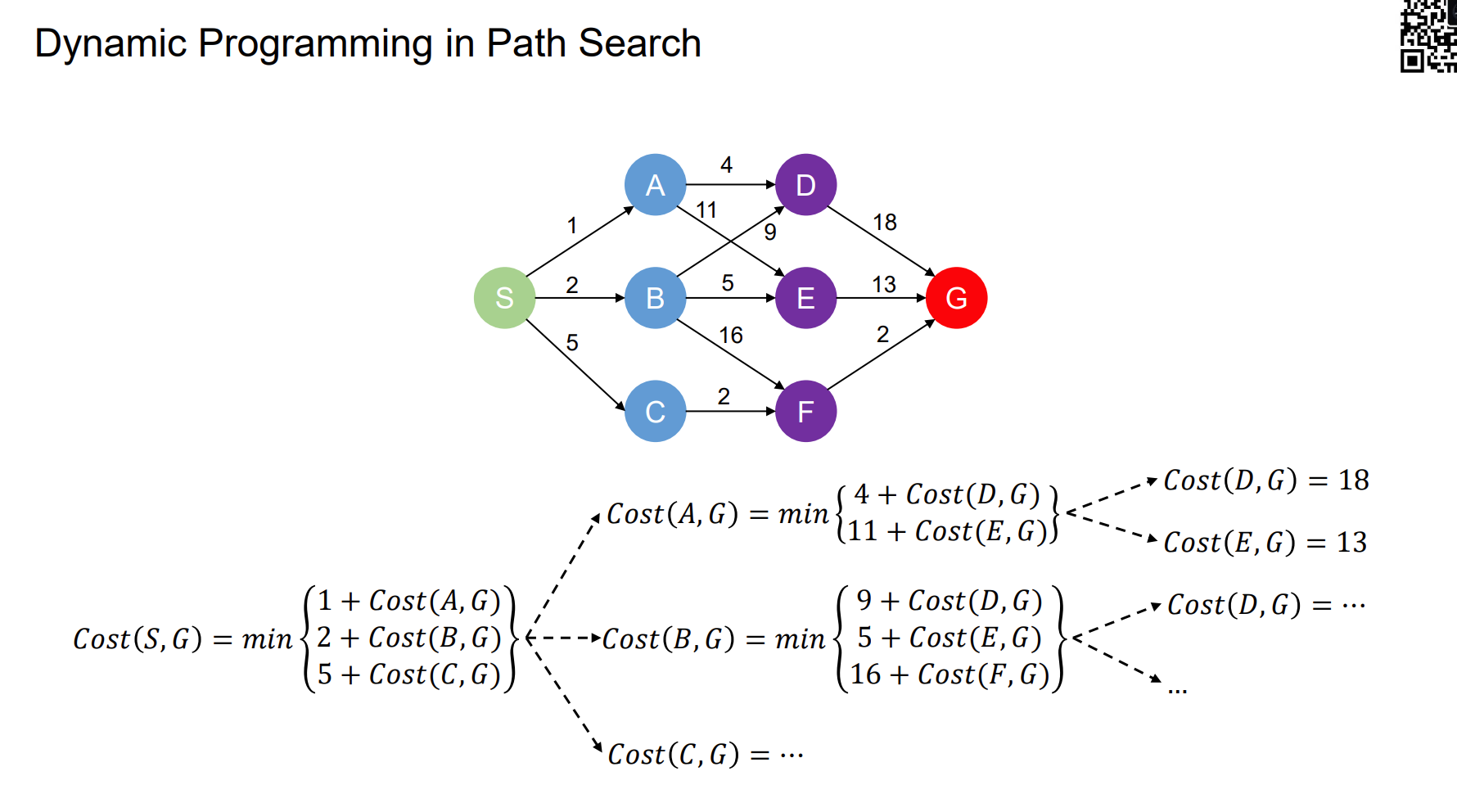
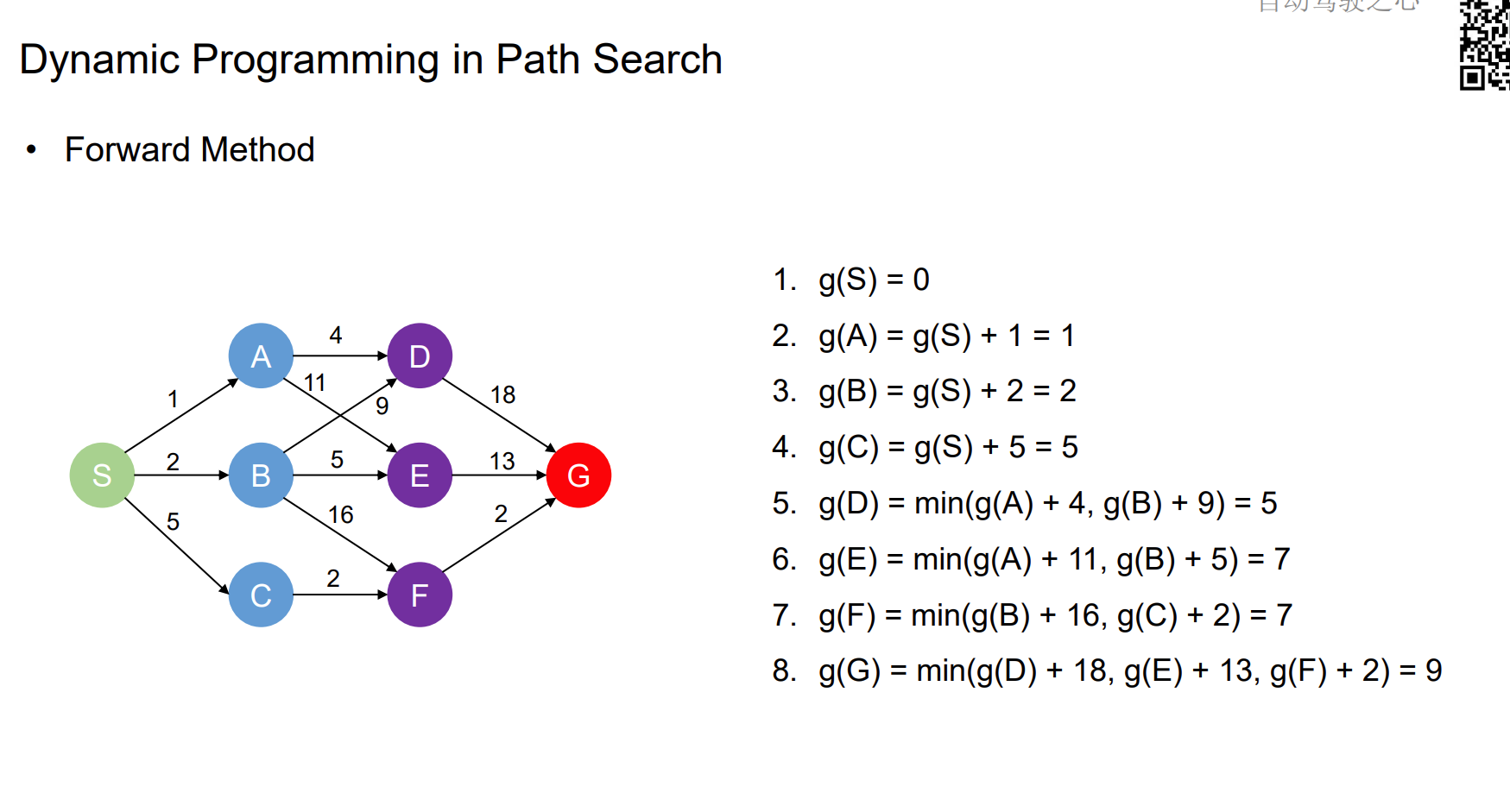
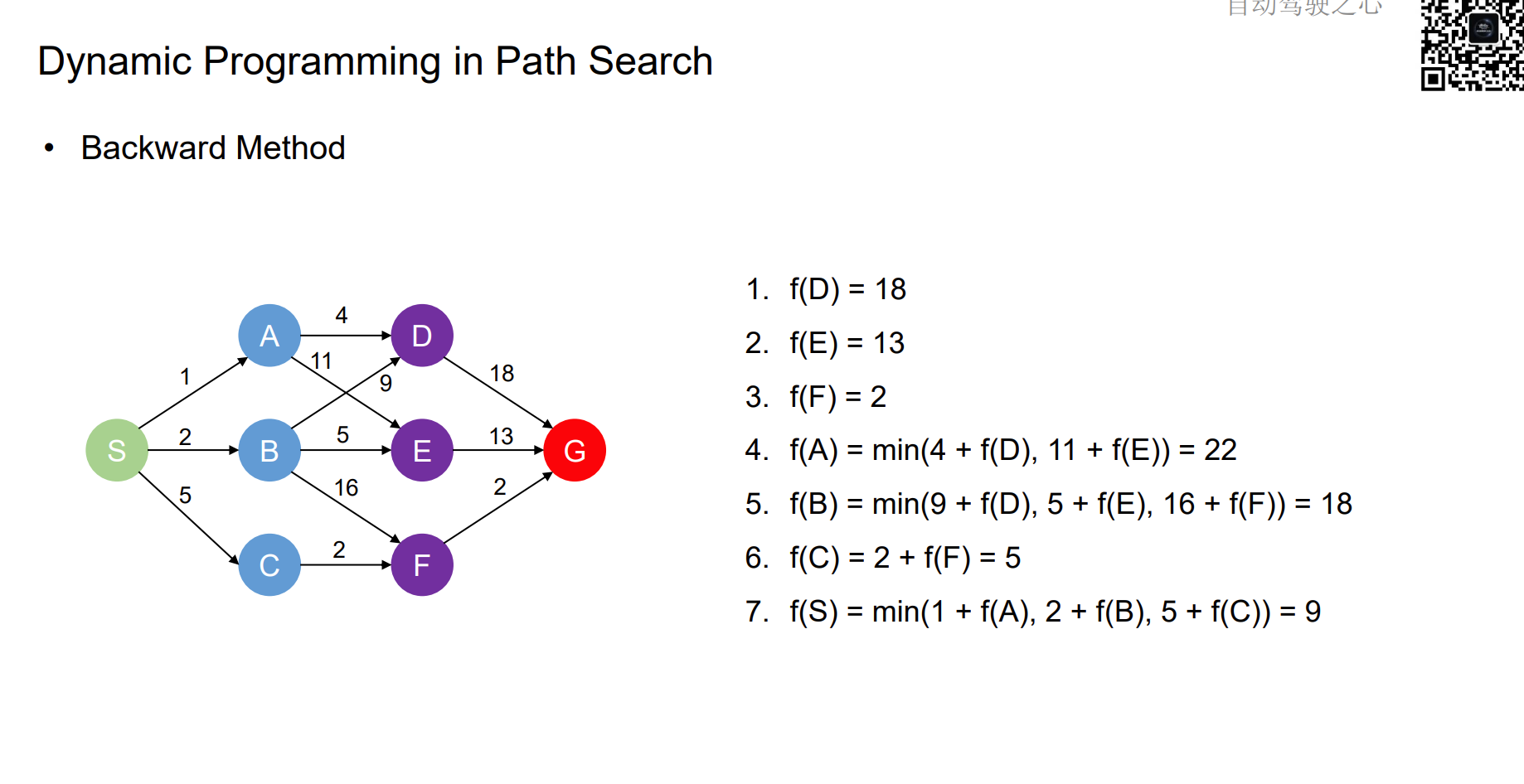
Dynamic Programming in Path Search
Sampling-based Planning Methods
General Recipe

Probabilistic Roadmap (PRM)
PRM
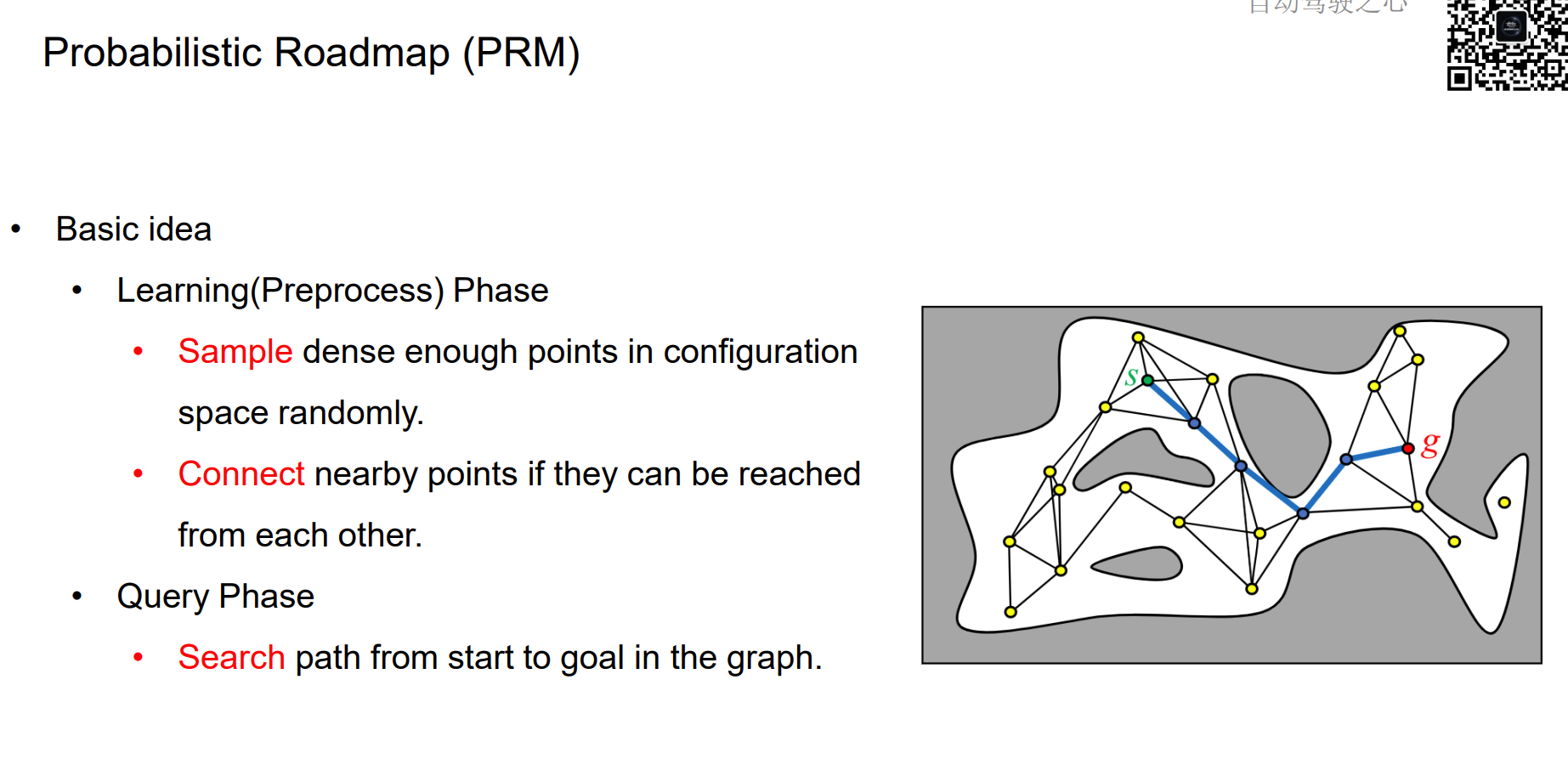
1、撒点来学习出图的结构,得到一个graph
2、用图搜索来搜索出最优的路径
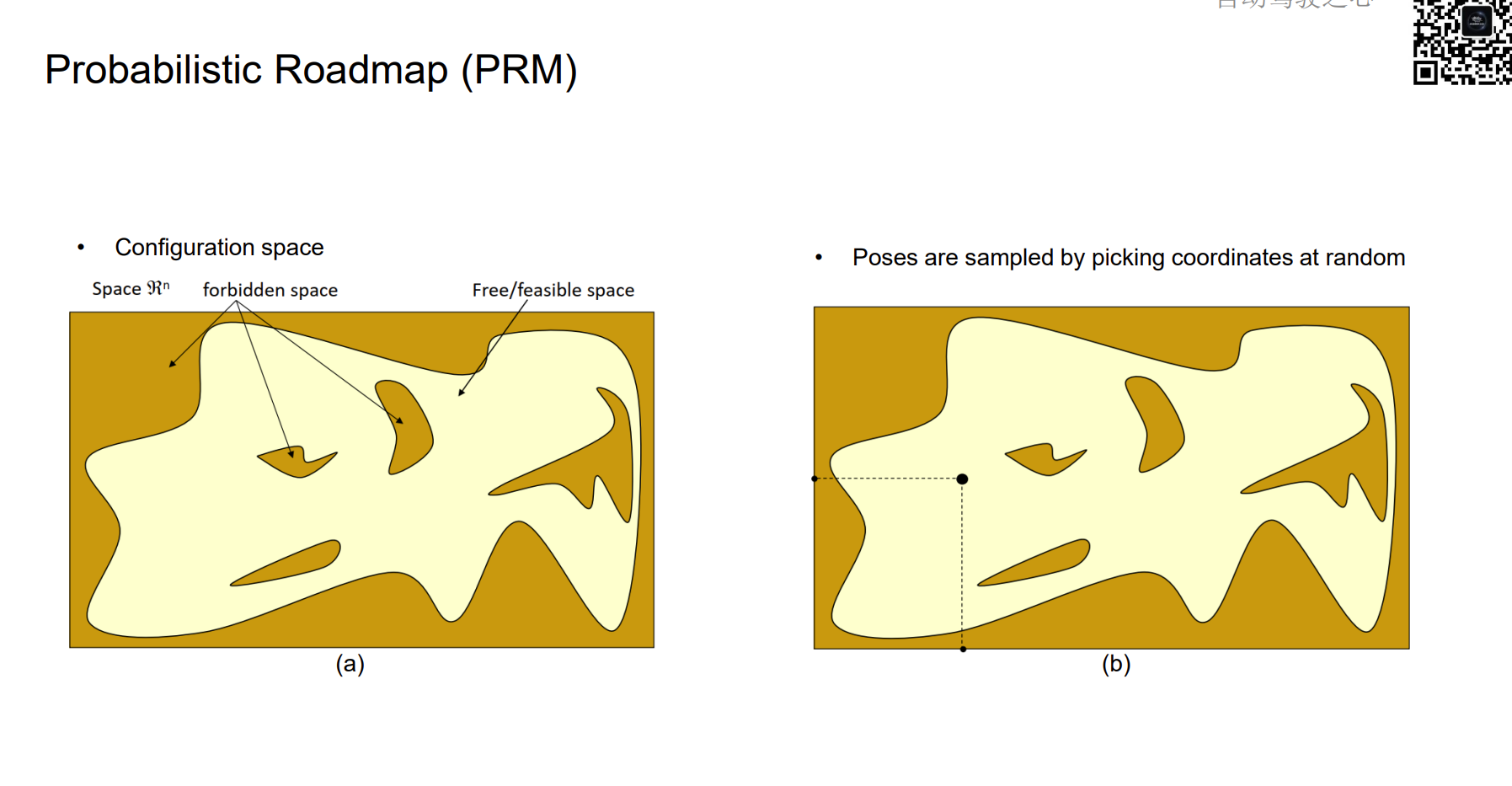
配置空间是指,在这样空间中规划的其实是一个质点,机器人的几何信息都被近似到forbidden space里面了。
对于图中的freespace来说,只要质点是在图中,那么可以忽略机器人几何形状的影响。
随机采样:依据某种分布,在一定范围内随