题目：
给定 N 个闭区间 [ai,bi]，请你将这些区间分成若干组，使得每组内部的区间两两之间（包括端点）没有交集，并使得组数尽可能小
输出最小组数

第一行包含整数 N，表示区间数
接下来 N 行，每行包含两个整数 ai,bi，表示一个区间的两个端点

输出一个整数，表示最小组数

1 ≤ N ≤ 10^5,
−109 ≤ ai ≤ bi ≤ 10^9

输入:
3
-1 1
2 4
3 5

输出：
2

public class 区间分组 {
    //all存储所有区间的l和r，q代表当前共有多少个区间组
    public static int N = 1000010, n;
    public static Range[] all = new Range[N];
    public static PriorityQueue<Integer> q = new PriorityQueue<>();

    public static void main(String[] args) {
        //读入
        Scanner in = new Scanner(System.in);
        n = in.nextInt();
        for (int i = 0; i<n; i++) {
            int l = in.nextInt(), r = in.nextInt();
            all[i] = new Range(l ,r);
        }

        //根据区间的左端点的值，从小到大sort
        Arrays.sort(all, 0, n);

        //遍历所有区间
        //对于每个区间有两种情况:
        //1.如果当前q中的区间组的最小Max_r大于等于当前区间r的左端点(也就是和所有区间组有交集)，那么说明当前区间应该新开一组
        //2.不符合条件1,说明q中最小Max_r小于当前区间的左端点(也就是和最小Max_r这个区间没有交集)，那么说明当前区间可以加到最小Max_r的区间中
        for (int i = 0; i<n; i++) {
            Range r = all[i];
            if (q.isEmpty() || q.peek() >= r.l) q.add(r.r);
            else {
                q.poll();
                q.add(r.r);
            }
        }

        System.out.println(q.size());
    }
}

//定义一个区间类，l表示左端点，r表示右端点，定义区间类的compareTo方法
class Range implements Comparable<Range>{
    int l, r;

    public Range(int l, int r) {
        this.l = l; this.r = r;
    }

    @Override
    public int compareTo(Range other) {
        return this.l - other.l;
    }
}

思路：
1.将每个区间按照左端点的值，从小到大进行排序
2.从前往后枚举每个区间
判断能否将当前区间x放入任何已存在的区间组当中（x的左端点 > 任意区间组的Max_r）：

1. 如果不行（说明x和所有区间组有交集），那么就新开一组，将x的右端点放进去
2. 如果可以（说明x和一些区间组没有交集），那么就将放入的那一组的Max_r更新为x的右端点值

根据这样的思路，我们可以将其简化一下，使用小根堆来判断条件，因为我们想快速判断当前区间x能否放入某个区间组中，那么我们只要记录每个区间组的Max_r即可，更新的时候也是直接拿最小的Max_r对比即可

以题目为例：
-1 1和2 4可以分为一组，因为这两个区间没有交集
3 5单独分为一组，因为他和已经存在的区间组（-1 1，2 4）有交集
也可以用Max_r来判断，区间组中的最右端点是4 > 当前区间的左端点3，说明3 5不能放入这个区间组中

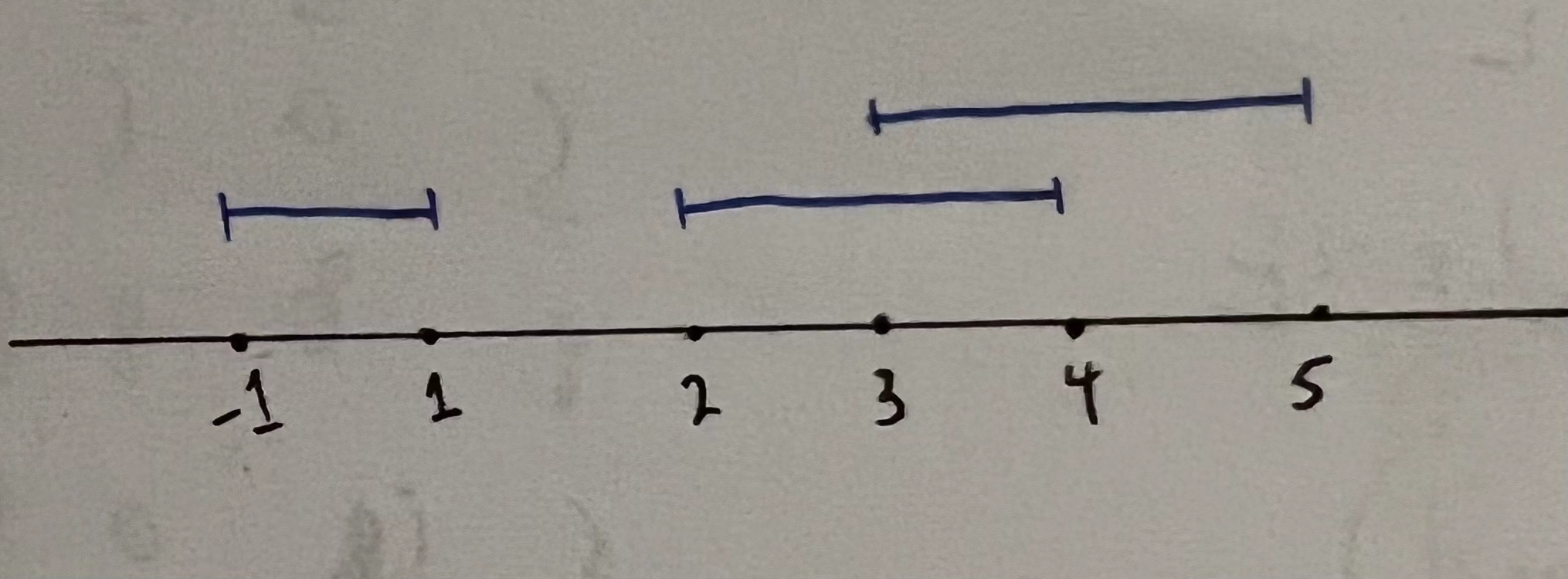
声明：
算法思路来源为y总，详细请见https://www.acwing.com/
本文仅用作学习记录和交流