参考资源:
- 视觉目标跟踪SiamRPN
- SiameseRPN详解
- CVPR2018视觉目标跟踪之 SiameseRPN
目录)
- 1. 模型架构
- 1.1 Siamese Network
- 1.2 RPN
- 2. 模型训练
- 2.1 损失函数
- 2.2 端到端训练
- 2.3 正负样本选择
- 3. 跟踪阶段
- 总结
SiamRPN是在SiamFC的基础上进行改进而得到的一种新架构。与基础的SiamFC相比,其添加了RPN(Region Proposal Network,区域建议网络)模块,从而避免了多尺度测试(multi-scale test),并提高了执行速度,同时,RPN中对anchor box的运用使得其输出的跟踪框准确度更高。
除此之外,SiamRPN的另一个特点在于其可以基于稀疏数据来进行训练,这代表可以用更多的数据来对网络进行训练(稀疏标记的数据集所包含的数据量会比精确标记的数据集大得多),而在目标跟踪领域,更多的训练数据往往意味着更好更鲁棒的模型性能。
RPN首次被提出是在Faster R-CNN: T owards Real-Time Object Detection with Region Proposal Networks这篇文章中,也就是大名鼎鼎的Faster RCNN,可以通过阅读这篇RCNN Fast R-CNN Faster R-CNN总结(学习笔记)来详细了解其原理。
1. 模型架构
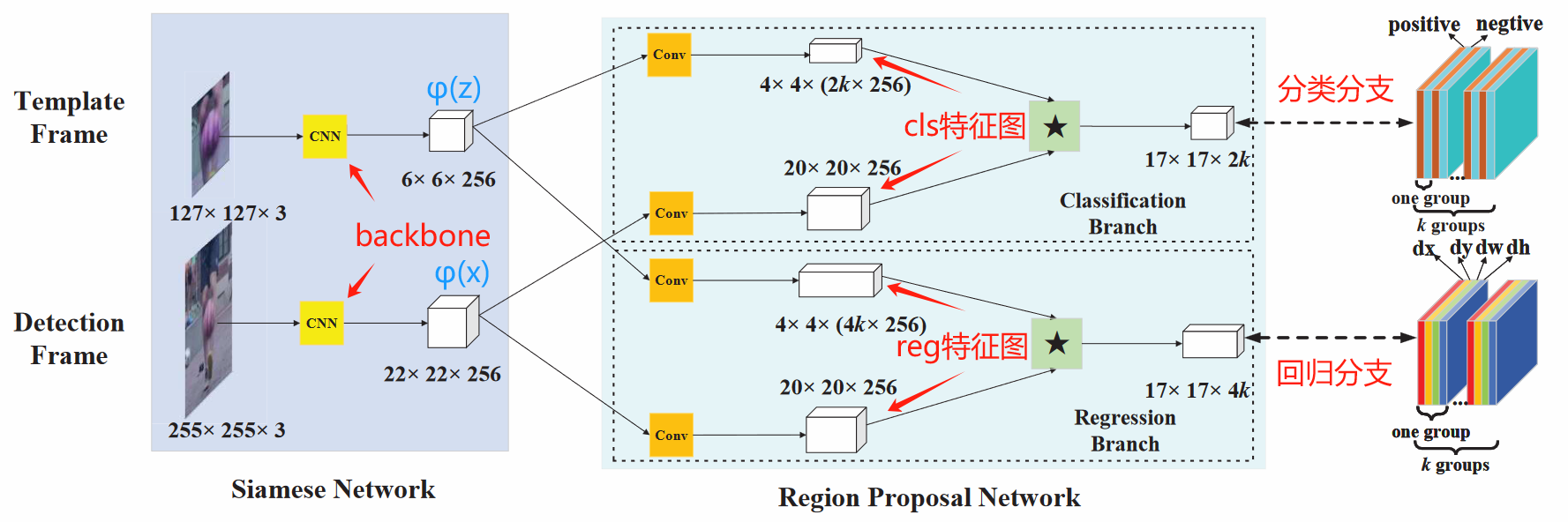
SiamRPN的主要网络架构如上图所示,可以分为两个部分:
-
与SiamFC一样,包括一个Siamese网络用于特征提取,分别提取模板帧和检测帧(搜索区域)的图像特征。这个步骤是用同一个CNN实现的,即backbone。也就是说,尽管在图中看起来好像分别用了两个CNN来提取特征,但是实际上模板特征提取分支和检测区域特征提取分支共用同一个CNN。
-
提取完的特征被送入Region Proposal Network,该子网络应用anchor机制对bounding box(边界框)进行预测。anchor,也称anchor box,是预先定义好的候选边界框。我们定义一组anchor boxes,并默认这组框能够覆盖到所有状态时刻的跟踪目标。
基于Siamese网络提取到的抽象特征,RPN网络通过分类分支来得到每一个anchor box包含跟踪目标的置信度(也就是将其分类为目标/背景),同时通过回归分支将可能包含目标的候选框(置信度高的anchor box)的位置和长宽进行微调,以使得微调后的anchor box能够完美包裹住跟踪目标(anchor是预设的,其长宽比、位置都是固定的,数量有限,因此不微调的话很难总是包裹住跟踪目标)。
有关anchor,具体可以参考这篇目标检测中的anchor机制。如果看不懂可以看这篇RCNN Fast R-CNN Faster R-CNN总结(学习笔记)中有关anchor的部分。
1.1 Siamese Network
Siamese Network,译为孪生网络,代表该子网络由两个分支组成,可以参考网络架构图。孪生网络接受两个输入,一个是template frame(模板帧),一个是detection fame(检测帧),其中,模板帧从视频的第一帧中由人工勾选出来,检测帧则是从视频流中除了第一帧以外的其它帧中crop出来的(这里是指实际推理阶段,训练阶段的模板帧和检测帧的选择方式是不同的)。
实际上,这两个分支的卷积神经网络共享权重(因为都是为了提取抽象特征,只不过一个是提取模板,一个是提取检测区域,所以可以共享),即,在代码实现中,只包含一个网络。
需要注意的是,Siamese子网络采用全卷积网络,即不包含padding,以满足平移不变性。关于什么是平移不变性,可以参考这篇【深入思考】卷积网络(CNN)的平移不变性和这篇卷积神经网络中的平移不变性,看了之后受益良多。
除此之外,原论文中还提到:
We use a modified AlexNet pretrained from ImageNet with the parameters of the first three convolution layers fixed and only fine-tune the last two convolution layers in Siamese-RPN. These parameters are obtained by optimizing the loss function in Eq. 5 with SGD
这里表示SiamRPN用了古老的AlexNet来进行特征提取。至于为什么不用新一点的ResNet来进行特征提取,这个原因将在SiamRPN++中提及。这里不作过多解释。
Siamese网络分别提取模板帧 z z z和检测帧 x x x的特征,并分别生成6×6×256的特征图 φ ( z ) \varphi(z) φ(z)和22×22×256的特征图 φ ( x ) \varphi(x) φ(x)。
1.2 RPN
从SiameseRPN结构图可以看到,RPN子网络有两个分支,一个分支叫做分类分支,另一个分支叫做回归分支。每个分支都接收 φ ( z ) \varphi(z) φ(z)和 φ ( x ) \varphi(x) φ(x)通过卷积层改变维度后的两个特征图作为输入。
对于分类分支,其接收 [ φ ( z ) ] c l s [\varphi(z)]_{cls} [φ(z)]cls和 [ φ ( x ) ] c l s [\varphi(x)]_{cls} [φ(x)]cls作为输入,对于回归分支,其接收 [ φ ( z ) ] r e g [\varphi(z)]_{reg} [φ(z)]reg和 [ φ ( x ) ] r e g [\varphi(x)]_{reg} [φ(x)]reg作为输入。其中,通过图中被黄色标注的3×3卷积核后, φ ( z ) \varphi(z) φ(z)分别产生了4×4×(2k×256)的 [ φ ( z ) ] c l s [\varphi(z)]_{cls} [φ(z)]cls和4×4×(4k×256) 的 [ φ ( z ) ] r e g [\varphi(z)]_{reg} [φ(z)]reg。
这里从6×6的尺寸经过3×3的卷积核得到4×4的特征尺寸比较简单,值得注意的是特征通道从256上升到了2k×256以及4k×256。对于分类分支,之所以特征通道上升了2k倍,是因为在特征图的每个点都预设了k个anchor,分类分支预测每个anchor是背景还是目标,总共有2类,所以是从256变成了256×2k。同理,每个anchor可以用 ( x , y , w , h ) (x,y,w,h) (x,y,w,h)来描述,共有4个参数,因此,对于需要微调这4个参数的回归分支,其特征图通道从256上升成了256×4k。检测帧的特征 φ ( x ) \varphi(x) φ(x)在经过卷积层后,也被分成两个分支特征 [ φ ( x ) ] c l s [\varphi(x)]_{cls} [φ(x)]cls和 [ φ ( x ) ] r e g [\varphi(x)]_{reg} [φ(x)]reg,但保持通道数不变。
之后,将模板图像上全部2k个anchor的4×4×256特征与检测图像的20×20×256特征进行相关操作,从而产生分类分支响应图,对于回归分支,也是类似的操作,最终,分别生成17×17×2k的分类响应图
A
w
×
h
×
2
k
c
l
s
A^{cls}_{w\times h\times 2k}
Aw×h×2kcls和17×17×4k的回归响应图
A
w
×
h
×
4
k
r
e
g
A^{reg}_{w\times h\times 4k}
Aw×h×4kreg:
A
w
×
h
×
2
k
c
l
s
=
[
φ
(
x
)
]
c
l
s
⋆
[
φ
(
z
)
]
c
l
s
A
w
×
h
×
4
k
r
e
g
=
[
φ
(
x
)
]
r
e
g
⋆
[
φ
(
z
)
]
r
e
g
(1)
A^{cls}_{w\times h\times 2k}=[\varphi(x)]_{cls}\star[\varphi(z)]_{cls}\\ A^{reg}_{w\times h\times 4k}=[\varphi(x)]_{reg}\star[\varphi(z)]_{reg}\tag{1}
Aw×h×2kcls=[φ(x)]cls⋆[φ(z)]clsAw×h×4kreg=[φ(x)]reg⋆[φ(z)]reg(1)
其中,
⋆
\star
⋆代表的是卷积操作,相当于用卷积核
[
φ
(
z
)
]
c
l
s
[\varphi(z)]_{cls}
[φ(z)]cls和
[
φ
(
z
)
]
r
e
g
[\varphi(z)]_{reg}
[φ(z)]reg来对
[
φ
(
x
)
]
c
l
s
[\varphi(x)]_{cls}
[φ(x)]cls和
[
φ
(
x
)
]
r
e
g
[\varphi(x)]_{reg}
[φ(x)]reg进行卷积操作。
2. 模型训练
2.1 损失函数
在训练过程中,使用cross-entropy loss(交叉熵损失)作为分类分支的损失函数,使用smooth L1 loss作为回归分支的损失函数。交叉熵损失函数比较常见了。这里主要介绍一下smooth L1 loss:
之前说过,一个anchor可以用
(
x
,
y
,
w
,
h
)
(x,y,w,h)
(x,y,w,h)来描述,其中,
x
x
x和
y
y
y描述了anchor的中心点坐标,
w
w
w和
h
h
h则描述了anchor的宽和高。假设,跟踪目标的真实边界框(bounding box)为
(
T
x
,
T
y
,
T
w
,
T
h
)
(T_x,T_y,T_w,T_h)
(Tx,Ty,Tw,Th),而此时有个anchor十分接近这个边界框,其anchor box为
(
A
x
,
A
y
,
A
w
,
A
h
)
(A_x,A_y,A_w,A_h)
(Ax,Ay,Aw,Ah),那我们的回归目标则为:
δ
[
0
]
=
T
x
−
A
x
A
w
,
δ
[
1
]
=
T
y
−
A
y
A
h
δ
[
2
]
=
ln
T
w
A
w
,
δ
[
3
]
=
ln
T
h
A
h
(2)
\delta [0]=\frac{T_x-A_x}{A_w},\space\space\delta [1]=\frac{T_y-A_y}{A_h}\\ \delta [2]=\ln\frac{T_w}{A_w}, \space\space\space\space\space \delta [3]=\ln\frac{T_h}{A_h}\tag{2}
δ[0]=AwTx−Ax, δ[1]=AhTy−Ayδ[2]=lnAwTw, δ[3]=lnAhTh(2)
在这个回归目标的基础上,应用smooth L1损失,smooth L1损失为:
s
m
o
o
t
h
L
1
(
x
,
σ
)
=
{
0.5
σ
2
x
2
,
∣
x
∣
<
1
σ
2
∣
x
∣
−
1
2
σ
2
,
∣
x
∣
≥
1
σ
2
(3)
smooth_{L_1}(x,\sigma)=\begin{cases}0.5\sigma^2x^2, \space\space|x|<\frac{1}{\sigma^2} \\ |x|-\frac{1}{2\sigma^2},|x|\ge\frac{1}{\sigma^2}\tag{3} \end{cases}
smoothL1(x,σ)={0.5σ2x2, ∣x∣<σ21∣x∣−2σ21,∣x∣≥σ21(3)
其中,
σ
\sigma
σ是控制平滑区域范围的超参数。不同的
σ
\sigma
σ值决定了在何处从平方损失过渡到绝对值损失。则,回归分支的损失函数为:
L
r
e
g
=
∑
i
=
0
3
=
s
m
o
o
t
h
L
1
(
δ
[
i
]
,
σ
)
(4)
L_{reg}=\sum^3_{i=0}=smooth_{L_1}(\delta[i],\sigma)\tag{4}
Lreg=i=0∑3=smoothL1(δ[i],σ)(4)
最后,总的损失函数为:
l
o
s
s
=
L
c
l
s
+
λ
L
r
e
g
(5)
loss=L_{cls}+\lambda L_{reg}\tag{5}
loss=Lcls+λLreg(5)
其中,
λ
\lambda
λ是用于平衡两个分支损失的超参数。
2.2 端到端训练
训练阶段,首先应用Imagenet对Siamese子网络进行了预训练。之后,再应用Youtube-BB数据集和ILSVRC数据集对整个SiameseRPN进行了端到端的训练(基于SGD)。由于训练回归分支需要更多的数据量,因此文中提到采用了数据增强方法,如仿射变换。
除此之外,作者提到了:
We choose less anchors in tracking task than detection task by noticing that the same object in two adjacent frames won’t change much. So only one scale with different ratios of anchor is adopted and the anchor ratios we adopted are [0.33, 0.5, 1, 2, 3].
也就是说,考虑到相邻帧之间目标不会发生太大的变化,因此和传统的RPN会在特征图的每个点生成三种尺度和三种宽高比即3×3=9种anchor相比,SiameseRPN只会考虑一种尺度和5种宽高比即1×5=5种anchor,所采用的宽高比为 [ 1 3 , 1 2 , 1 , 2 , 3 ] [\frac{1}{3},\frac{1}{2},1,2,3] [31,21,1,2,3]。
-
对于模板帧和检测帧的选取,在训练阶段,模板帧和检测帧来自于同一个视频流中的同一个目标的两帧。为了更好地学习目标的变换,模板帧和检测帧分别取自不同的帧,且这两帧之间有一定的随机间隔(间隔小于100,因为过远的间隔会导致目标的变换过大)。
-
假设目标的边界框(bounding box)大小为 ( w , h ) (w,h) (w,h),则我们将从全局图像中裁剪一个大小为 A × A A\times A A×A的patch作为模板帧, A A A的定义如下:
( w + p ) × ( h + p ) = A 2 (6) (w+p)\times(h+p)=A^2\tag{6} (w+p)×(h+p)=A2(6)
其中, p = ( w + h ) 2 p=\frac{(w+h)}{2} p=2(w+h)。之后,裁剪得到的patch被resize到 127 × 127 127\times127 127×127大小。检测帧基于同样的方式被crop出来,但是其大小是模板帧的两倍,同时resize到 255 × 255 255\times255 255×255大小。
2.3 正负样本选择
使用IOU作为判断正负样本的标准,设置高(0.6)和低(0.3)两个阈值,正样本为IOU>0.6的anchor和其对应的ground truth,负样本则为IOU<0.3的anchor。同时,还限制了一个training pair中包含64个样本,其中正样本最多16个。
3. 跟踪阶段
在原文的第4节Tracking as one-shot detection中,作者将跟踪任务描述为了one-shot detection检测任务。首先,其在4.1节对什么是one-shot detection进行了公式化的建模,得到了下述公式:
min
W
1
n
∑
i
=
1
n
L
(
ζ
(
φ
(
x
i
;
W
)
;
φ
(
z
i
;
W
)
)
,
ℓ
i
)
(7)
\min\limits_W \frac{1}{n} \sum_{i=1}^n \mathcal{L}(\zeta (\varphi(x_i;W);\varphi(z_i;W)),\ell_i)\tag{7}
Wminn1i=1∑nL(ζ(φ(xi;W);φ(zi;W)),ℓi)(7)
4.1节比较好理解,这里不对公式(7)作过多解释。建议仔细阅读原文。
比较难理解的是4.1节的最后一段。我翻来覆去看了很多遍,才有一点自以为是的感悟,现分享如下:
We can now reinterpret the template branch in Siamese subnetwork as training parameters to predict the kernel of the local detection task, which is typically the learning to learn process. In this interpretation, the template branch is used to embed the category information into the kernel and the detection branch performs detection using the embedded information. During the training phase, the meta-learner doesn’t need any other supervision except the pairwise bounding box supervision. In the inference phase, Siamese framework is pruned only leaving the detection branch except the initial frame thus leading to high speed. The target patch from the first frame is sent into the template branch and the detection kernel is pre-computed so that we can perform one-shot detection in other frames. Because the local detection task is based on the category information only given by the template on initial frame, it can be viewed as one-shot detection.
首先用三种颜色标注这段话中比较重要的三个部分。对于每个部分,分别解释如下:
-
红色部分,直译过来是:将连体子网络中的模板分支重新解释为预测local detection task内核的训练参数。
看回到公式(1),还记得上面提到的:最终用于分类预测和回归预测的响应图是用卷积核 [ φ ( z ) ] c l s [\varphi(z)]_{cls} [φ(z)]cls和 [ φ ( z ) ] r e g [\varphi(z)]_{reg} [φ(z)]reg来对 [ φ ( x ) ] c l s [\varphi(x)]_{cls} [φ(x)]cls和 [ φ ( x ) ] r e g [\varphi(x)]_{reg} [φ(x)]reg进行卷积操作得到的吗?也就是说,这里是把模板帧的特征图当成卷积核,在检测帧的特征图上进行卷积。这里十分关键,模板帧的特征图是“卷积核”,则特征图的值就可以被理解为CNN中卷积核训练好的参数值,而特征图又是由模板分支得到的,因此,模板分支的参数相当于什么?是不是就可以相当于训练过程中咱们人工设置好的超参数?
对吧,类比卷积神经网络的卷积核参数(训练后得到)和训练网络用的超参数(训练前人工设置得到)的关系,就可以理解这句话。并且,在训练阶段,模板分支的参数是不是会被训练?一旦训练结束,到测试阶段,模板分支的参数就固定了,基于固定的模板分支参数和不同的输入检测帧,我们可以得到不同的特征图,也就相当于,基于同样的超参数和不同的数据集,我们能够训练出不同的卷积核。看到这里应该能大概理解红色部分语句的意思了,句中的local detection task的内核其实就是指的是基于模板分支提取得到的模板帧特征图。
-
蓝色部分,直译过来是:在这种解释下,模板分支用于将类别信息嵌入内核,而检测分支则利用嵌入的信息执行检测。
理解了红色部分,蓝色部分就更好理解了。将类别信息融入内核指的就是模板分支提取模板帧的深度特征,然后生成特征图,即“内核”,然后,检测分支利用特征图中蕴含的深度特征,进行互相关操作,以生成响应图,来生成对anchor类别和边界框回归的预测。
-
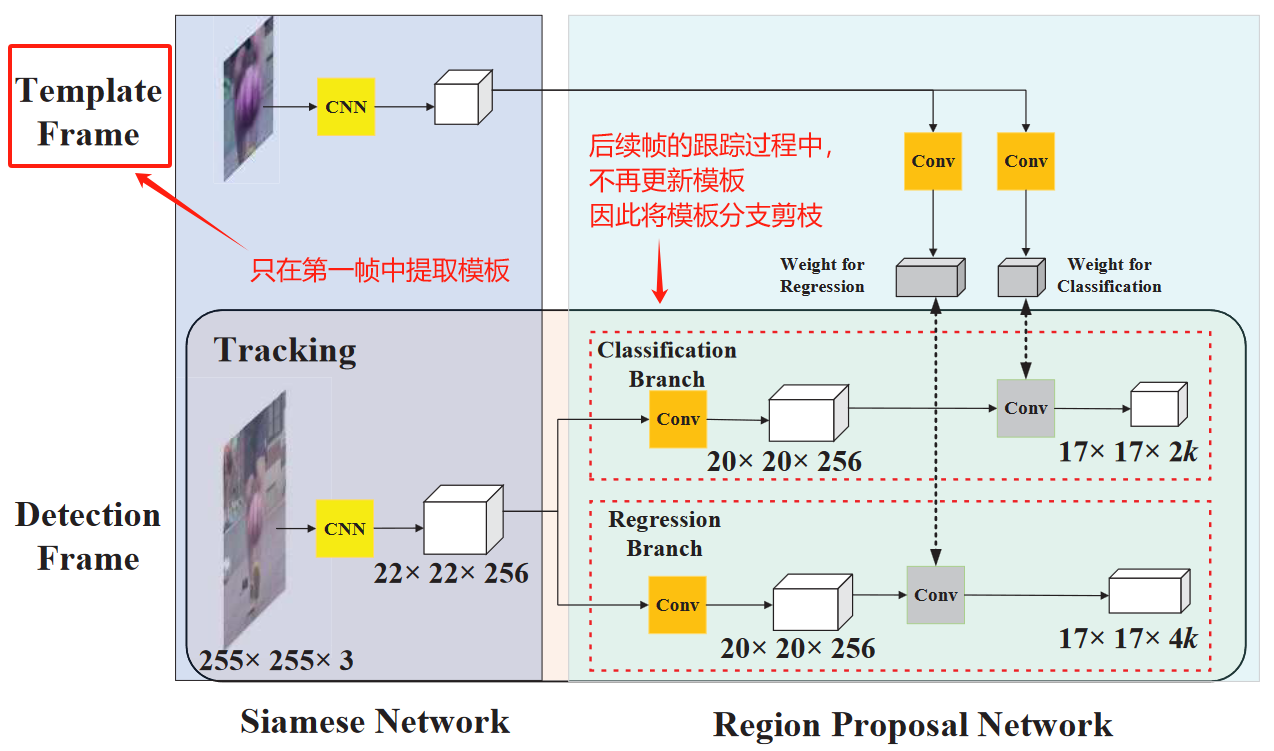
橙色部分,直译过来是:在推理阶段,除初始帧外,Siamese框架只在检测分支中剪枝,因此速度很快。第一帧的目标patch被送入模板分支,并预先计算检测内核,这样我们就可以在其他帧中执行单次检测。由于local-detection task仅基于初始帧模板提供的类别信息,因此可以将其视为一次检测。
这里也很好理解,可以参考下图,在推理阶段(实际跟踪阶段),SiameseRPN只在第一帧中生成模板帧,并通过模板分支计算得到特征图,也就是local-detection的“内核”。在之后的跟踪过程中,为了保证模板的准确性,当然,也是相信深度卷积神经网络能够提取得到足够有用和准确的特征,SiamRPN不再对模板进行更新,因此只需通过模板分支计算一次模板帧的特征图。这也是为什么作者将跟踪任务视为local-detection task的原因,因为算法只使用了初始帧模板提供的类别信息。
4.2节主要是对推理过程进行了数学建模(自己看一下!很好懂!),最终,基于前 K K K个分类置信度最高的anchor boxes,和回归分支对这 K K K个anchor boxes的回归预测,得到 K K K个更精确(相较于anchor)的proposals。
由于这 K K K个proposals不一定完全准确,因此作者提出了两种策略来选择保留哪些proposals:
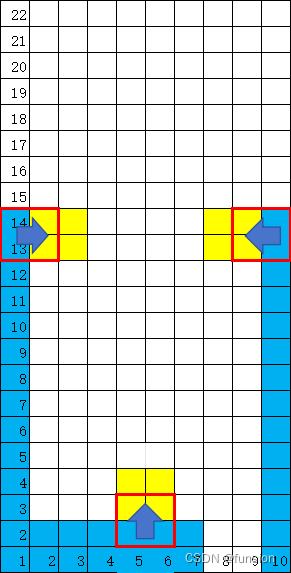
- 策略一:抛弃远离中心的anchor生成的proposals,例如,只保留中心 g × g g\times g g×g区域的anchor圣成的proposals,这个策略是考虑到相邻帧间目标不会有太大的运动。实际代码中, g g g被设置为7。
- 策略二:使用余弦窗口和比例变化惩罚来对这 K K K个proposals进行re-rank(重新排名)。
最后,进行NMS(非极大值抑制),然后选择排名第一的proposal作为最终的输出。在确定最终边界框后,通过线性插值更新目标尺寸,以保持形状的平滑变化。
总结
了解RPN和SiamFC的话,可以很容易地理解SiameseRPN的架构和核心思想。还没跑过代码,希望有时间试试。