💕"对相爱的人来说,对方的心意,才是最好的房子。"💕
作者:Lvzi
文章主要内容:算法系列–递归,回溯,剪枝的综合应用(3)
大家好,今天为大家带来的是
算法系列--递归,回溯,剪枝的综合应用(3),带来几个比较经典的问题N皇后和解数独,这两道都是hard级别的题目,但是不要被吓到!请看我的分析
1.N皇后
题目链接:
https://leetcode.cn/problems/n-queens/description/

分析**
1.画决策树
理解题目的意思之后可以开始画决策树,决策树其实也好画,我们只需枚举每一行可能的位置即可,下面是当N = 3时的决策树:
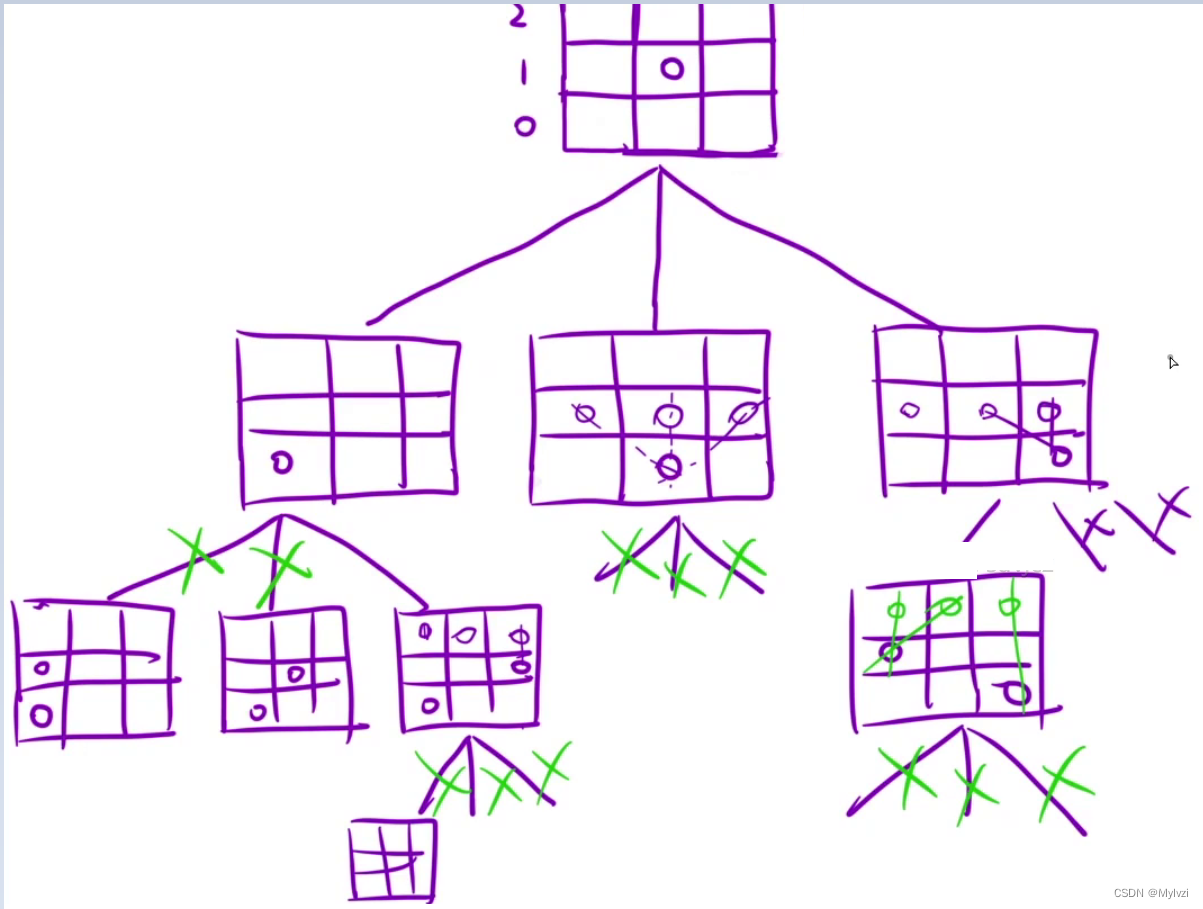
每一层干的事情:
- 枚举当前行所有的位置,如果可以放皇后,就放,并递归下一行
- 如果不可以放—剪枝
2.剪枝(本题的难点)
这里先不设计代码,先进行剪枝的操作,分析上图,当我们在某个位置放皇后的时候一定要保证该位置行,列,主对角线,副对角线上没有其他皇后

其实当前行不需要考虑有没有皇后,因为我们是一行一行枚举的,所以只需要考虑列,主对角线,副对角线上没有其他皇后即可
那该怎么判断呢?可能会想到使用3层for循环去遍历与当前位置相关的位置:
- 第一层循环遍历当前位置所在列有无皇后
- 第二层循环遍历当前位置的
主对角线上有无皇后 - 第三层循环遍历当前位置
副对角线上有无皇后
如果在遍历的过程中发现了皇后,则该皇后会攻击当前要填位置的皇后,所以不能放皇后–剪枝
但是此时的时间复杂度高达3n * 2 ^ n,时间复杂度很高(但是在本题也能通过),其实我们可以采用之前学习过的五子棋中判断当前位置的相关位置有无棋子的策略–使用三个布尔类型的数组
boolean[] col:用于标记当前列上有无皇后boolean[] digit1:用于标记当前位置的主对角线上有无皇后boolean[] digit2:用于标记当前位置的副对角线上有无皇后

3.设计代码
全局变量
ret:最终的返回值path:记录每次dfs的结果,类型设置为char[][],方便填充- 三个布尔类型的数组
N:用于表示皇后的个数
dfs
- 函数头:只需要告诉我当前遍历到哪一行就行–一个参数
row - 函数体:每一个子问题都是
从0开始遍历当前行的所有位置,符合条件的位置添加Q,并递归下一行,不符合条件的位置什么也不干 - 递归出口:当
row==N,即遍历到完所有行后
4.剪枝:
不符合条件的位置直接跳过即可
5.回溯:
回溯只需要将原先填充的位置恢复原状,并将对应位置的三个布尔类型的数组更改为false
代码:
class Solution {
List<List<String>> ret;// 返回值
char[][] path;// 记录每次搜索的结果
boolean[] col;// 列
boolean[] digit1;// 主对角线
boolean[] digit2;// 副对角线
int N;
public List<List<String>> solveNQueens(int n) {
N = n;
ret = new ArrayList<>();
path = new char[N][N];
for(int i = 0; i < n; i++)// 预处理 全部填充为. 后续只需要考虑符合条件的情况即可
Arrays.fill(path[i],'.');
col = new boolean[N];
digit1 = new boolean[2 * N];
digit2 = new boolean[2 * N];
dfs(0);
return ret;
}
private void dfs(int row) {
// 递归出口
if(row == N) {
// 添加结果
List<String> tmp = new ArrayList<>();
for(int i = 0; i < N; i++)
{
tmp.add(new String(path[i]));
}
ret.add(new ArrayList<>(tmp));
return;
}
for(int i = 0; i < N; i++) {
if(!col[i] && !digit1[i - row + N] && !digit2[i + row]) {
path[row][i] = 'Q';
col[i] = digit1[i - row + N] = digit2[i + row] = true;
dfs(row + 1);// 递归下一行
path[row][i] = '.';// 回溯
col[i] = digit1[i - row + N] = digit2[i + row] = false;
}
}
}
}
总结:
- path是一个二维的字符数组,path[0]代表一个
char[],字符数组就是一个字符串,然后创建一个List类型的集合去依次添加path每一行的元素即可 - 将path数组使用
Arrays.fill()将path全部填充为.,这样在后面遍历的时候只需要考虑为Q的情况即可 - 注意在填充的时候一定要创建
新的引用,不要直接添加,因为引用指向的是堆上的地址,你后续的更改会影响集合中存储的内容的 - i代表列数,row是行数,明确每一个变量的实际意义
2.有效的数独
注:本题只是一个引子,是为了给解数独这道题目做引入
链接:
https://leetcode.cn/problems/valid-sudoku/description/

分析:
本题需要判断已经填入数字的数独是否有效,判断条件和N皇后那道题目的剪枝策略很像,具体的判断条件如下:
- 当前数字所在位置的相同
行不能有相同的数字 - 当前数字所在位置的相同
列不能有相同的数字 - 当前数字所在位置所处的
九宫格不能有相同的数字
行和列只需要使用两个二维的布尔类型的数组进行标记即可,但是九宫格这个判断条件如何标记呢?这里用到了一个比较巧妙的策略,将连续的三个位置看成一个数字,

代码:
class Solution {
boolean[][] row, col;
boolean[][][] grid;
public boolean isValidSudoku(char[][] board) {
row = new boolean[9][10];
col = new boolean[9][10];
grid = new boolean[3][3][10];
for(int i = 0; i < 9; i++) {
for(int j = 0; j < 9; j++) {
if(board[i][j] != '.') {
int num = board[i][j] - '0';
if(col[j][num] == true || row[i][num] == true || grid[i / 3][j / 3][num] == true)
return false;
col[j][num] = row[i][num] = grid[i / 3][j / 3][num] = true;
}
}
}
return true;
}
}
3.解数独
链接:
https://leetcode.cn/problems/sudoku-solver/description/

分析:
很容易分析出本题是一个递归问题,因为每一步做的事情都是相同的
- 存入数字,判断是否符合条件
递归的策略也容易想出–以一个一个的空格进行枚举

1.设计代码
全局变量
row[][],col[][]分别用于标记行和列grid[][][]:用于标记九宫格
dfs:
- 函数头:只需要传递原始的棋盘即可,返回值设置为boolean
- 函数体:关注每一个子问题具体干的事情,在当前空位置从数字1枚举到数字9,判断是否符合添加的条件,如果可以,就填入,并递归下一个空位置
- 递归出口:全部填充完毕
2.剪枝
注意有可能上一步的策略会导致当前位置无法填入任何数字,也就是上一步的策略是否有效需要递归到后面的子问题才能知道,一旦某个子问题中发现无法填入任何数字,证明上一步的策略是失败的,没有必要继续递归下去,此时就发生了剪枝,对于每一次递归来说,都需要返回一个布尔类型的数据,用于记录策略成功与否
3.回溯
回溯的策略和N皇后很像,恢复原状即可
代码:
class Solution {
boolean[][] row, col;
boolean[][][] grid;
public void solveSudoku(char[][] board) {
row = new boolean[9][10];
col = new boolean[9][10];
grid = new boolean[3][3][10];
// 初始化
for(int i = 0; i < 9; i++) {
for(int j = 0; j < 9; j++) {
if(board[i][j] != '.') {
int num = board[i][j] - '0';
row[i][num] = col[j][num] = grid[i / 3][j / 3][num] = true;
}
}
}
// 递归
dfs(board);
}
private boolean dfs(char[][] board) {
// 这里采用的递归的策略是一个一个空位置进行递归的
for(int i = 0; i < 9; i++) {
for(int j = 0; j < 9; j++) {
if(board[i][j] == '.') {
for(int num = 1; num <= 9; num++) {
if(!row[i][num] && !col[j][num] && !grid[i / 3][j / 3][num]) {// 剪枝
board[i][j] = (char)('0' + num);
row[i][num] = col[j][num] = grid[i / 3][j / 3][num] = true;
// 递归下一个位置
if(dfs(board) == true) return true;// 当前位置的策略是成功的
board[i][j] = '.';// 回溯
row[i][num] = col[j][num] = grid[i / 3][j / 3][num] = false;
}
}
return false;// 走到这里证明当前位置一个数字也填不了,需要更换上一步的策略
}
}
}
return true;// 所有的空位都被填充
}
}
一定要重点理解代码中三个return的实际含义

(本题真的很有意思,你可以利用上述代码快速的完成一道大师级的数独题目哦~笔者已经试过一次,真的很爽!!!)