参考资料：python统计分析【托马斯】

1、例子

        假设你在经营一家私立教育机构，你的合同显示：如果全国平均水平时100分时，你的学生在期末考试中得了110分，你就能获得奖金；若结果明显降低，你就会失去奖金。

学生得分数据如下：109.4,76.2,128.7,93.7,85.6,117.7,117.2,87.3,100.3,55.1

图像展示如下：

# 导入库
# 用于数值处理的库
import numpy as np
import pandas as pd
import scipy as sp
from scipy import stats
# 用于绘图的库
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
#录入学生成绩
scores=np.array([109.4,76.2,128.7,93.7,85.6,117.7,117.2,87.3,100.3,55.1])
x=np.arange(0,10)
#制作学生成绩散点图
plt.scatter(x,scores)
plt.axhline(110,linestyle=":")
plt.axhline(np.mean(scores),linestyle="-.")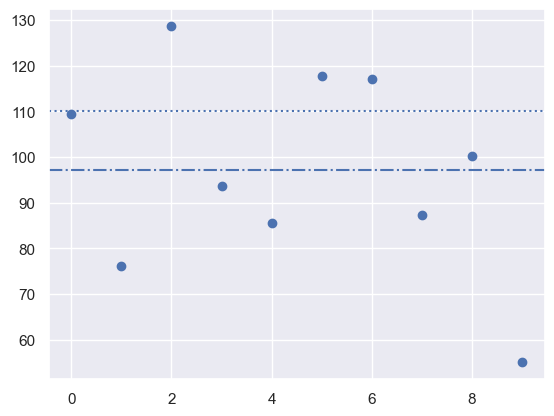

        现在我们想知道：分数的均值97.1是否和110显著不同？

首先进行正态性检验：

stats.normaltest(scores)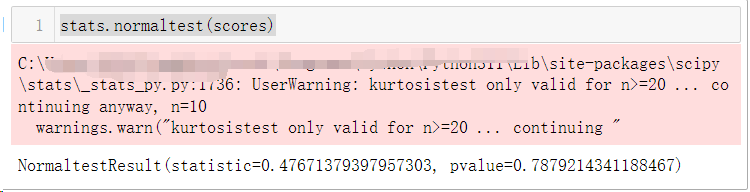

        正态性检验（stats.normaltest()）表示数据很可能来自一个正态分布。由于我们不知道我们检验的学生结果的总体方差，我们必须尽力去猜测样本方差。同时我们知道样本均值和总体均值之间的标准化的差异，即来自t分布的t统计量。

        我们样本的均值和我们想比较的值的差值是-12.9。通过样本标准差进行标准化后得到t=-1.84。因为t分布只依赖于样本数量且是一条已知的曲线，我们可以通过下面代码计算得到|t|>1.84的t统计量的可能性。

# 计算t值
tval=((110-np.mean(scores))/stats.sem(scores))
print("t-value: ", tval)
# 设置t分布
td=stats.t(len(scores)-1)
# 计算p值
p=2*td.sf(tval)
print(p)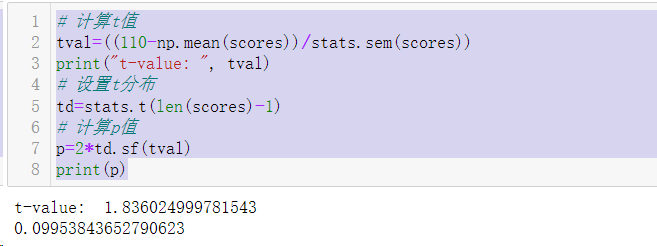

        之所以用2*td.sf(tval)，是因为我们必须综合考虑两个概率，t<-1.84和t>1.84。考虑到我们的样本数据，我们可以声明总体均值是110的可能性是9.95%。由于我们习惯上将低于5%的可能性能认为是统计学差异，我们可以作出结论：观察到的97.1并没有和110显著不同。

2、推广和应用

（1）推广

        基于前面的例子，假设检验的一般步骤如下所述：

        ①从总体中抽取一个随机样本。

        ②构建一个无效假设（即零假设）。

        ③计算一个我们已知概率分布的检验统计量。

        ④比较观测值的统计量和对应分布，我们可以得到一个和观测值同样极端或更极端的概率，就是所谓的p值。

        如果p值小于0.05，我们拒绝无效假设，并声称有统计学显著差异。

        和p值进行比较的相对值是显著性水平，经常用字母α来表示。

        这种对建设进行检验的方式叫做统计学推断。

        请记住：p值仅仅表示在无效假设为真的情况下，得到一个确定的检验统计量的值的可能性。

（2）其他案例

        ①让我们比较两组受试者的体重。零假设是两组体重之间不存在差异。如果统计学比较体重产生的p值为0.03，这意味着，零假设是正确的概率是3%。由于这个概率小于0.05，我们说，“两组的体重有显著差异”。

        ②如果我们要检验一个假设，即一个组的平均值是7，么个相应的零假设将是：“我们假设总体的平均值和7之间没有差异。”

        ③（正态性检验）如果我们检查一个数据样本是否服从正态分布，零假设就是“我的数据和正态分布的数据之间没有什么区别”：这里大的p值表示数据实际上是正态分布。

3、p值的解释

        零假设的p<0.05的值被解释为：如果零假设是真的，找到比观察到的统计量同样极端或更极端的一个检验统计量的机会小于5。这并不是说零假设是错误的，但更不能说另一种假设是正确的。

4、错误的类型

        假设检验中，会发生两种类型的错误。

（1）Ⅰ类错误

        Ⅰ类错误是指无效假设是真的时候，结果是显著的。Ⅰ类错误的可能性经常用α表示，并且该值在数据分析前就确定了。在质量控制中，Ⅰ类错误被叫作生产者风险，因为你在一个产品符合规范要求的情况下拒绝了它。

（2）Ⅱ类错误

        Ⅱ类错误是，尽管无效假设是错误的，但结果是不显著。在质量控制中，Ⅱ类错误被叫做消费者风险，因为消费者获得了一个不符合规范要求的产品。这类错误的概率通常表示为β。一个统计检验的“效能”被定义为(1-β)×100，并且这也是正确的接受备择假设的概率。

（3）解释p值的陷阱

        换句话说，p值测量的是假设的证据。不幸的是，p值经常被错误的看待成拒绝假设的错误概率，或者更糟糕的是，认为是假设为真的后验概率。

5、样本量

        一个二元假设的灵敏度/效能是当备择假设是真的时候，检验正确地拒绝了无效假设的概率 。

        决定统计学检验的效能和计算揭示一定大小效能所需要的最小样本来量，叫作效能分析。它包括4个因素：

        ①α，Ⅰ类错误的概率；

        ②β，Ⅱ类错误的概率；

        ③d，效能的大小，即所研究的效应相对样本的标准差σ的大小；

        ④n，样本大小。

        这4个参数中只有3个可以被选择，第4个自动地被固定。

（1）案例

        如果我们有这样一个假设，即我们抽样的总体均值为x1，标准差为σ，实际的总体均值为x1+D，标准差也是σ，我们可以用最小的样本量来找到这样的差异：

        其中，z是标准化的正态变量：

        并且，是效应的大小。

        总的来说，如果真是的均值是x1，我们想要在1-α的检验中正确地检测；如果真是的均值偏移了D或更多，我们想要在至少1-β的概率下检测到。

        为了找到两组正态分布均值之间的差异，它们的标准差分别是σ1和σ2，为了检测出绝对差异是D，所需要的每组最小样本量是：

（2）python实现

        statsmodels很巧妙地利用了上面提到的4个变量中有3个是独立的这个事实，它将其与python一个“具名参数”的特征结合起来，提供了一个程序，接受这些参数中的三个作为输入，并计算剩下的第4个参数。例如：

# 导入库
import numpy as np
from scipy import stats
from statsmodels.stats import power


nobs=power.tt_ind_solve_power(
    effect_size=0.5,
    alpha=0.05,
    power=0.8
)
print(nobs)

        代码结果告诉我们，如果我们比较两个具有相同个体数和相同标准差的组别，需要α=0.05和检验效能80%，并且我们想检验的组间差异是标准差的一半大，那么我们需要每组64个个体。

effect_size=power.tt_ind_solve_power(
    alpha=0.05,power=0.8,nobs1=25)
print(effect_size)

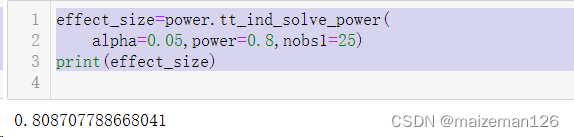
        此代码结果告诉我们：如果我们的α=0.05，检验效能为80%，每组有25个个体，那么组间差异最小是样本标准差的81%。