RRBE
本文仅供自我学习使用,切勿转载和搬运,如有侵权,联系立删~
方法总框架
首先由内容所有者生成原始图像像素点的标签映射; 然后数据隐藏者采用自适应霍夫曼编码将多个信息插入加密图像像素点;接收端进行数据提取和图像恢复。在数据提取之前,必须对标记的加密图像进行置乱以增强安全性。

方法细节介绍
A 生成Label map
保留第一行、第一列的像素作为参考像素,使用中值边缘检测器(MED)进行像素预测。根据预测像素和原始像素的八位二进制序列相同位数来确定每个像素的Label。注意参考像素的Label设置为-1。以下图为例:
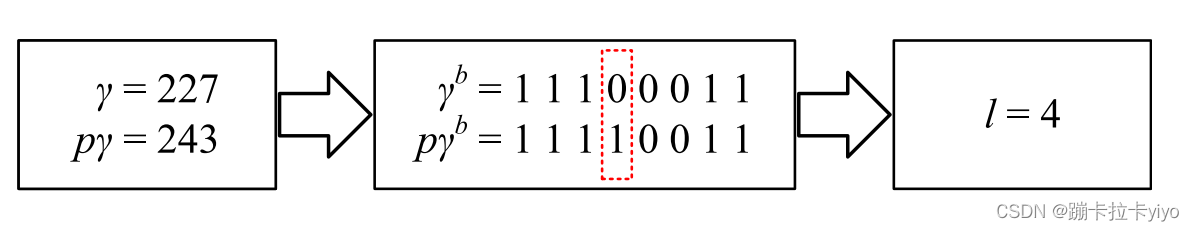
当标签为4时,说明该位置可以嵌入的bit数为4,在恢复时,MSB-(-1)位与预测像素相同,第
位与预测像素相反。
B EC的几何变换及比较
在生成具体的Label map之前,对图像进行几何变换和比较。分别用00、01、10、11表示原图和三个几何变换
、
、
的图像,以下图为例