自然语言处理3（NLP）—

1. 自然语言处理在机器学习领域的主要任务

自然语言处理（NLP）在机器学习领域中扮演着至关重要的角色，旨在使计算机能够理解、解释和生成人类语言。以下是NLP在机器学习领域中的主要任务及其分类方法：

1.1 按照功能类型分类

1.1.1 分类任务

分类任务是指将输入数据分配给预定义类别中的一类的过程。在NLP中，这通常涉及文本或文档的分类，比如情感分析（将文本分类为正面或负面情感）、垃圾邮件检测（判断邮件是否为垃圾邮件）和话题分类（确定文本所属的主题或类别）。

1.1.2 结构预测任务

结构预测任务是指预测输入数据的结构化输出的任务。在NLP中，一个典型的例子是句法分析，其中模型需要从给定的句子中预测句法树。

输入：自然语言句子。
输出：句子的句法树，展示了句子中词汇元素之间的句法关系，如主谓宾结构、修饰关系等。

1.1.3 序列标注任务

序列标注任务涉及到为输入文本序列中的每个元素（通常是单词或字符）分配一个标签或类别。这类任务的例子包括命名实体识别（NER），其中需要识别文本中的特定实体（如人名、地名、组织名等），以及词性标注（POS tagging），即确定句子中每个单词的词性（如名词、动词、形容词等）。

输入：文本序列。
输出：对于输入序列中的每个元素，输出一个对应的标签序列。

1.1.4 回归任务

回归任务是指预测一个连续值而非分类标签的任务。在NLP中，回归任务可以用于估计文本的某些属性，如文本相关性评分、情感强度评估等。

输入：文本或文档。
输出：一个连续的数值，表示文本的某种量化属性（如情感强度、相关性评分等）。

这些任务展示了NLP在机器学习领域的多样性和复杂性。通过结合先进的机器学习技术，NLP旨在深入理解和处理自然语言数据，从而支持广泛的应用，包括自动翻译、智能助手、信息检索和内容分析等。

1.2 按照学习方法分类

在自然语言处理（NLP）领域，根据训练数据的标注情况，机器学习任务通常可以分为有监督学习、无监督学习和半监督学习。这三种方法各有优势和局限，适用于不同的场景和需求。

1.2.1 有监督的学习

有监督学习是指利用一组已经被手动标注的数据（训练集）来训练模型的过程。每个训练样本都包含一个输入和一个期望的输出标签。有监督学习任务在NLP中非常常见，如文本分类、情感分析、命名实体识别等。

手动标注：这个过程需要大量的人力来为数据集中的每个实例提供准确的标签。虽然这增加了成本和时间，但通常可以得到性能更好、更可靠的模型。

1.2.2 无监督的学习

无监督学习不依赖于标注数据，而是试图直接从无标注的数据中学习模式和结构。无监督学习适用于数据标注成本高昂或者标注资源稀缺的场景，如主题发现、词义聚类、文档聚类等。

从无标注的数据学习：这种方法节省了大量的人类标注成本，但性能通常比有监督学习低。然而，通过发掘数据本身的内在结构，无监督学习能够揭示出数据中未被标注的潜在信息。

1.2.3 半监督的学习

半监督学习结合了有监督学习和无监督学习的优点。它使用少量标注数据和大量无标注数据一起训练模型。这种方法旨在通过无标注数据来增强模型的泛化能力，同时利用有限的标注数据确保模型学习到正确的任务特定信息。

结合有标注和无标注数据：半监督学习适用于标注数据有限但未标注数据丰富的场景。这种方法可以显著减少人工标注的需求，同时保持或甚至提高模型性能。

这三种学习方法在自然语言处理任务中广泛应用，选择哪种方法取决于特定任务的需求、数据的可用性和标注资源的限制。通过适当选择学习策略，可以有效地处理自然语言数据，解决各种复杂的NLP问题。

2 模型与概率的概念

2.1 模型Models

在自然语言处理（NLP）和机器学习领域中，模型是对现实世界数据和现象进行高度抽象和简化的数学表达。这些模型能够帮助我们理解数据的内在结构，预测未来事件，或者从数据中自动提取有价值的信息。下面详细介绍概率模型的相关概念和组成部分。

2.1.1 概率模型

概率模型是使用概率论的方法来表达变量之间关系的模型。在NLP中，概率模型尤其重要，因为自然语言的生成和理解本质上是不确定和多变的。是随机事件概率的可能性。对随机事件的概率进行估算。

2.1.2 训练样本和训练数据集

训练样本：单个数据点或例子，通常包括输入数据及其对应的输出数据。在NLP任务中，一个训练样本可以是一个文本及其对应的标签（如情感分类中的正面或负面）。
训练数据集：一组训练样本的集合，用于训练模型。通过分析训练数据集中的模式和关系，概率模型可以学习到如何将输入映射到输出。

2.1.3 建模的对象

建模的对象是我们希望模型学习和预测的现实世界现象。在NLP中，这可能是文本的类别、文本中某个单词的下一个单词、文本的情感倾向等。

2.1.4 建模的训练和训练的原则

建模的训练：指的是使用训练数据集来调整模型参数的过程。训练目的是让模型能够准确地从输入数据预测输出数据。
训练的原则：最大似然估计（MLE）是训练概率模型的一种常见原则。通过最大化训练数据的似然函数，MLE寻找最佳的模型参数，使得模型产生观测数据的概率最大。

2.1.5 概率的语言模型

概率的语言模型是NLP中一种重要的概率模型，用于计算一系列词汇（即文本）出现的概率。这种模型通常用于各种任务，如语音识别、机器翻译、拼写纠错等。语言模型通过学习大量文本数据，能够预测给定前面词汇后，下一个词汇是什么。

2.1.6 掷骰子的概率模型

掷骰子的概率模型是一个经典的例子，用来说明如何应用概率理论来建模和分析随机事件。假设我们有一个标准的六面骰子，每个面分别标记为1到6。我们想要建立一个模型来描述掷骰子结果的概率分布。

2.1.6.1 模型的定义

在这个模型中，每次掷骰子的结果可以是1、2、3、4、5或6，这六种结果构成了我们的样本空间，即所有可能发生的结果。

2.1.6.2 样本的前提

公平骰子：假设骰子是公平的，即每个面朝上的概率都是相同的。
独立事件：每次掷骰子的结果是独立的，即一次掷骰的结果不会影响下一次掷骰的结果。

2.1.6.3 概率分布

基于上述假设，每个面朝上的概率都是 $1/6$ 。我们可以将这个概率分布写为：

$P(1) = 1/6$
$P(2) = 1/6$
$P(3) = 1/6$
$P(4) = 1/6$
$P(5) = 1/6$
$P(6) = 1/6$

其中， $P(x)$ 表示骰子掷出结果为 $x$ 的概率。

2.1.6.4 概率模型的应用

这个简单的概率模型可以用来解答各种关于掷骰子的概率问题，比如：

        单次掷骰子：计算掷出特定数字的概率（如上所述）。
        多次掷骰子：计算在多次掷骰中出现特定组合的概率。例如，掷两次骰子都得到6的概率是 $(1/6) \times (1/6) = 1/36$ 。
        期望值：计算掷骰子的期望值，即平均来看每次掷骰子得到的数字。对于公平的六面骰子，期望值为 $E(X) = (1+2+3+4+5+6)/6 = 3.5$ 。

这个模型虽然简单，但它展示了如何使用概率理论来建立和理解随机事件的数学模型，这对于理解更复杂的概率模型和统计分析是非常重要的基础。

总之，概率模型在NLP和机器学习领域中扮演着核心角色，通过对数据进行建模、训练和预测，它们能够帮助我们理解和生成自然语言。最大似然估计是训练这些模型的一个重要原则，它通过最大化模型生成训练数据的概率来寻找最佳的模型参数。

2.2 最大似然估算

最大似然估计（Maximum Likelihood Estimation, MLE）是一种统计方法，用于估计模型参数，使得观测到的数据在该模型参数下的概率（似然）最大。简而言之，MLE通过优化模型参数来找到最有可能产生观测数据的参数值。

2.2.1 如何工作

假设我们有一组观测数据和一个概率模型，该模型由一组参数决定。MLE的目标是找到这组参数的最佳值，以使观测数据出现的概率最大。

2.2.2 步骤

定义似然函数：似然函数是观测数据在模型参数下出现概率的函数。对于给定的数据集和模型，似然函数表示为这组数据在模型中的概率。

最大化似然函数：通过调整模型参数，找到使似然函数达到最大值的参数值。这通常通过求解似然函数的导数并设置为零来完成，求解得到的方程组可以给出参数的最佳估计值。

求解参数：最终，通过最大化似然函数获得的参数值就是我们估计的模型参数。

2.2.3 例子

让我们用一个简单的例子来解释最大似然估计（MLE）的概念：假设你有一枚不公平的硬币，想要估计这枚硬币正面朝上的概率（我们将这个概率记为 $p$ ）。

2.2.3.1 步骤 1: 进行实验

你抛了这枚硬币 10 次，记录下来的结果是：正面朝上 7 次，反面朝上 3 次。

2.2.3.2 步骤 2: 定义似然函数

似然函数表示的是，在给定参数 $p$ 下，观测到当前实验结果（正面朝上 7 次，反面朝上 3 次）的概率。根据二项分布，这个概率可以表示为：

$L(p) = p^7(1-p)^3$

其中， $L(p)$ 是似然函数， $p$ 是硬币正面朝上的概率。

2.2.3.3 步骤 3: 最大化似然函数

接下来，我们需要找到使 $L(p)$ 最大化的 $p$ 值。这通常通过对似然函数求导，然后令导数等于零来完成。对于这个例子：

$\frac{dL(p)}{dp} = 7p^6(1-p)^3 - 3p^7(1-p)^2 = 0$

解这个方程，我们可以找到使似然函数最大化的 $p$ 值。

简化这个过程，对于我们的特定情况，直觉上，最大似然估计的 $p$ 值会是正面出现的次数除以总次数，即 $p = \frac{7}{10} = 0.7$ 。这是因为在给定观测数据下， $p = 0.7$ 使得我们观测到这组数据的概率最大。

2.2.3.4 解释

所以，通过最大似然估计，我们估计说这枚硬币正面朝上的概率为 0.7。这意味着根据我们通过实验收集到的数据，我们最有信心认为这枚硬币落地正面朝上的概率为 70%。

这个例子展示了最大似然估计的直观思想：选择使观测到的数据出现概率最大的参数值。通过这种方式，MLE为我们提供了一种基于观测数据来估计未知参数的强大方法。

2.2.4 优点

        直观：最大似然估计的原理直观，即找到使数据出现概率最大的参数值。
        一致性：在一定条件下，随着样本量的增加，最大似然估计值会收敛到真实参数值。
        效率：在某些条件下，最大似然估计达到了所有无偏估计中方差最小的估计，即具有最小方差的无偏估计（MVUE）。

2.2.5 缺点

过拟合：在某些情况下，如果模型过于复杂，最大似然估计可能会导致过拟合，特别是当样本量较小时。
计算复杂性：对于复杂的模型，最大化似然函数可能涉及到复杂的数学运算，甚至可能没有解析解，需要使用数值方法求解。

最大似然估计在统计学、机器学习和许多其他领域中都有广泛的应用，是估计模型参数的一个基本和强大的工具。

2.3 随机事件与随机变量

让我用一个更简单的例子来解释随机事件和随机变量的概念：

2.3.1 随机事件

想象一下你在玩掷硬币游戏，硬币落地后可能正面朝上，也可能反面朝上。这里，“硬币正面朝上”或“硬币反面朝上”就是随机事件。这些事件是随机的，因为在你掷硬币之前，你无法确定硬币会怎样落地。

2.3.2 随机变量

现在，假设我们对这个掷硬币游戏稍微改变规则：我们不仅关心硬币是正面还是反面朝上，而且我们决定给每种结果打分。比如，如果硬币正面朝上，你得1分；如果硬币反面朝上，你得0分。

在这个例子中，得分就是一个随机变量。为什么这是一个随机变量呢？因为你得到的分数（1分或0分）取决于随机事件的结果（硬币是正面还是反面朝上）。换句话说，随机变量得分给了我们一个方法，通过它我们可以用数字（0或1）来表示掷硬币的随机结果。

如果硬币正面朝上，随机变量的值为1。
如果硬币反面朝上，随机变量的值为0。

2.3.3 总结一下

随机事件就是可能发生也可能不发生的事情，比如掷硬币的结果。

参数化：比如神经网络参数。
随机变量是一个数字，它基于随机事件的结果给出一个值，比如基于掷硬币结果给出的得分。

2.4 概率分布

概率分布是一个数学概念，用于描述随机变量取各种可能值的概率。它为我们提供了一种方式来表达或模拟不确定性和随机性。概率分布可以分为两大类：离散概率分布和连续概率分布。

2.4.1 离散概率分布

当一个随机变量的取值是有限的或者是可数的无限序列时，它的概率分布称为离散概率分布。离散概率分布给出了随机变量取每个可能值的概率。常见的离散概率分布包括：

二项分布：描述了在固定次数的独立试验中，成功（满足某条件）的次数。例如，抛10次硬币，正面朝上（成功）的次数。
泊松分布：描述了在一定时间或空间内，发生某事件的次数。例如，一小时内到达某网站的访问量。

2.4.2 伯努利分布与类别分布

伯努利分布和类别分布是概率论和统计学中两种常见的离散概率分布，它们在描述随机变量的概率分布时具有特定的应用场景。

2.4.2.1 伯努利分布

伯努利分布是最简单的离散分布之一，用于描述只有两个可能结果的单次随机试验。这两个结果通常被标记为成功（1）和失败（0）。伯努利分布的概率质量函数（PMF）由单个参数 $p$ 定义，其中 $p$ 是试验结果为成功的概率。因此，失败的概率为 $1-p$ 。伯努利分布的PMF可以写为： $P(X=x) = p^2x(1-p)^{1-x}$

其中 $x$ 取值为0或1。伯努利分布常用于描述单次的二元事件（如抛硬币），其中事件的结果只能是两种状态中的一种。

2.4.2.2 类别分布

类别分布（有时也称为多项分布的特例）是伯努利分布在多于两个结果的情况下的推广。它用于描述单次试验中有多个可能结果的情况，并且这些结果是互斥的。每个结果都有一个与之相关的概率，所有结果的概率之和为1。

如果我们有 $K$ 个可能的互斥结果，其中每个结果 $k$ 的概率为 $p_k$ ，则类别分布的概率质量函数可以表示为：

$P(X=k) = p_k$

其中 $k = 1, 2, ..., K$ ，且 $\sum_{k=1}^{K} p_k = 1$ 。

类别分布常用于描述单次试验的多种可能结果，例如掷一个多面骰子的结果，或者在多类分类问题中选择一个类别。

2.4.2.3 区别和联系

基本区别：伯努利分布描述的是一个二元（两种可能结果）的随机试验，而类别分布用于描述一个多元（多于两种可能结果）的随机试验。
联系：从某种意义上说，伯努利分布可以看作是类别分布在只有两个类别时的特例。当类别分布中的 $K=2$ 时，它实际上就是一个伯努利分布。

这两种分布都在数据分析、机器学习和统计推断中有广泛的应用，尤其是在处理分类数据和二元决策问题时。

2.4.3 连续概率分布

当一个随机变量可以取某个区间内的任何值时，它的概率分布称为连续概率分布。对于连续随机变量，我们通常关注变量落在某个区间内的概率，而不是取具体某个值的概率（这个概率在连续情况下为0）。常见的连续概率分布包括：

均匀分布：在某个区间内，随机变量取任何值的概率相同。例如，一个完美的随机数生成器生成0到1之间任何数的概率。
正态分布（高斯分布）：具有钟形曲线的分布，被广泛用于自然和社会科学。例如，人群中的身高分布。

2.4.4 概率分布的表示

对于离散概率分布，通常使用概率质量函数（PMF）来描述，它给出了随机变量取特定值的概率。
对于连续概率分布，使用概率密度函数（PDF）来描述，它并不直接给出随机变量取特定值的概率，而是随机变量落在某个区间内的概率可以通过PDF在该区间上的积分来计算。

概率分布是理解和描述随机现象的基础，它们在统计学、机器学习、工程和科学研究中有着广泛的应用。通过对概率分布的研究，我们可以对随机事件进行建模、预测和分析。

3. 文本的处理

3.1 齐普夫定律（Zipf's Law）

齐普夫定律（Zipf's Law）是一个关于词频分布的定律，描述了在自然语言处理和信息论中观察到的一种现象：一个文本中的任何单词的频率和它在频率排序中的位置成反比。也就是说，一个单词的频率大约等于它的排名的倒数。用数学表达式来说，如果 $r$ 是一个单词按频率降序排列的排名the rank of a word， $f$ 是它的频率frequency，那么 $f \approx \frac{1}{r}$ 。简单来说，这个定律认为在任何一篇文章或书籍中，最常见的单词出现的次数最多，第二常见的单词出现次数大约是最常见的单词的一半，第三常见的单词出现次数大约是最常见的单词的三分之一，以此类推。所以，如果一个单词的排名是第一，也就是它是最常见的，那么它出现的次数就是最多的。如果一个单词的排名是第二，它出现的次数就大约是排名第一的单词的一半。

以《白鲸记》（Moby Dick）为例，书中有189,910次单词occurrences出现，32,303种不同的单词形式forms，其中45,841个单词只出现了一次（hapaxes，即孤立词）。如果用这个定律来看《白鲸记》这本书，书中有大约19万次单词出现，超过3万种不同的单词形式。其中，有将近4.6万个单词只在书中出现了一次。根据齐普夫定律，这意味着《白鲸记》中最常见的那些单词出现的频率远远高于其他大部分单词。

这本书中出现最频繁的单词（排名第一）的频率会是出现第二频繁的单词频率的两倍，是第三频繁的三倍，以此类推。这个定律揭示了自然语言中词汇使用的一个有趣规律，即少数几个单词在文本中被高频使用，而大多数单词的使用频率则相对较低。

3.2 文本挖掘系统的架构示例Architecture of a text mining system

这张图展示的是一个文本挖掘系统的架构。我会按照图中的流程解释每一部分：

a.数据来源：系统从不同的在线资源（如网站、FTP资源WWW & FTP Resources

、新闻、电子邮件News and Email和其他在线资源Other Online Resources收集数据。

b.文档获取/爬取技术Document Fetching/ Crawling Techniques ：系统通过特定的技术获取或爬取这些在线资源的文档。

c.预处理任务Preprocessing Tasks ：在这个阶段，系统会对收集到的数据执行如分类Categorization,、特征/词项提取Feature/Term Extraction等任务。这是文本挖掘前的准备工作，目的是提取重要的信息，为后续的分析做准备。

d.处理后的文档集合Processed Document Collection ：预处理后的数据会被整理成一个处理后的文档集合，这些文档已被分类categorized、关键词标记keyword-labeled和时间戳标记。

e.压缩/层次化表示：这些处理后的文档可能会被进一步压缩或以层次化的方式表示，以便更有效地存储和处理。

f.知识源(Knowledge Sources)：系统可能会使用现有的知识库或数据库作为参考。

g.解析程序：这些程序用于解析处理后的文档和知识源中的数据。

h.文本挖掘发现算法Text Mining Discovery Algorithms：这个阶段，系统利用算法来识别模、趋势分析等。这是文本挖掘的核心部分，通过算法来发现文本数据中的有价值信息。

i.改进技术Refinement Techniques：在发现有价值的信息后，可能还需要进一步的改进技术，如抑制、排序、剪枝、泛化、聚类等，以提炼和优化结果。

j.浏览功能Browsing Functionality：系统提供了一系列的浏览功能，包括简单的过滤器、查询解释器、搜索工具、可视化工具、图形用户界面（GUI）和绘图功能，以便用户更好地理解和利用挖掘结果。

k.用户：最终，用户可以通过这些浏览功能和改进技术来查看和使用文本挖掘系统提取的信息。

l.背景知识(Backgroud Knowledge)：在整个过程中，用户的背景知识也会被用来辅助解释和理解文本挖掘结果。

整体来说，这个系统是从数据收集到信息提取和用户交互的完整流程。

3.3 文本预处理Preprocessing总揽

预处理是指在文本挖掘或自然语言处理中对文本数据集（语料库）进行处理，以便得到文档的表征（representation）。预处理就是在做文本分析前，先把文章或者文本资料做一些处理，让计算机更好地理解和分析这些文本。

下图展示了NLP预处理任务的层次和分类，它们是构建更复杂的NLP系统和应用的基础。

        文档表征是对文档内容的一种描述，它可以是简单的，也可以是复杂的：
        简单的表征可能只包括一些关键词或概念，这些关键词或概念可能来自于一个知识库。这个处理过程可能很简单，比如挑出一些重要的关键词或者概念。
        复杂的表征则可能是通过对文本进行更深入的语言分析得到的结果，比如通过词性标注、句法分析或语义分析等方法。比如详细地分析文本里的语言用法，包括每个词的词性（名词、动词等），句子的结构等等。

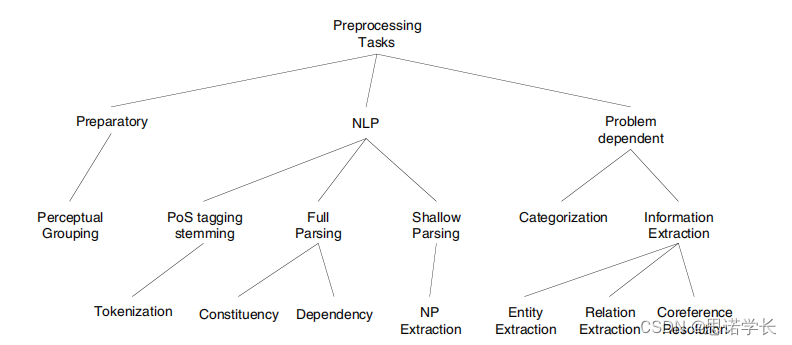
3.3.1 第一分枝：预备Preparatory

这一类任务是处理文本数据的基础步骤，通常在执行更复杂的NLP任务之前完成。 Perceptual Grouping（感知分类)是对文本进行初步的感知级别处理，将文本分成可管理的段落或单元，这可以视为预处理的一部分。可以看作是理解和处理文本数据的最初步骤，是在进行词性标注、词干提取和更深入的解析之前的基础工作。

3.3.2 第二分枝：NLP

这是图中的中心节点，表示所有的预处理任务都服务于NLP的更广泛目标。

3.3.2.1 词性标注和词干提取（PoS Tagging and Stemming）

词性标注和词干提取（PoS Tagging and Stemming）：词性标注是给文本中的每个单词分配一个词性（如名词、动词等），而词干提取是将单词还原为基本形式，去除词缀。
标记化（Tokenization）：这是将文本分割成更小单元（例如单词、短语或符号）的过程。将文本分割成单词或符号。

3.3.2.2 完整解析（Full Parsing）

完整解析（Full Parsing）：这是确定文本中单词之间关系的过程，包括句法结构和语义角色。

成分句法分析（Constituency）：用树状结构来分析句子的成分，如主语、谓语和宾语等。

依存句法分析（Dependency）：识别句子中单词之间的依赖关系，即哪些单词依赖于其他单词。

3.3.2.3 浅层解析（Shallow Parsing）

浅层解析（Shallow Parsing）：也称为块解析，它在完整解析和标记化之间，用于识别句子中的短语和有限的句法结构，但不进行完整的句法分析。

名词短语提取（NP Extraction）：特别关注于从文本中提取名词短语。

3.3.3 第三分枝：问题依赖性任务

这类任务通常是针对特定问题设计的，根据所面对的NLP问题的性质而定。

3.3.3.1 分类

分类（Categorization）：这是将文本分配到预定义类别的过程，例如文本分类或主题识别。

3.3.3.2 信息提取

信息提取（Information Extraction）：从文本中提取结构化信息的过程。

实体提取（Entity Extraction）：识别文本中的命名实体，如人名、地点、组织等。

关系提取（Relation Extraction）：识别实体之间的关系，例如谁是谁的CEO或哪个公司位于哪个城市。

指代消解（Coreference Resolution）：这是确定文本中的代词或指示词指向的实体的过程。

总的来说，预处理的目的是为了把原始文本转换成更适合计算机处理的形式，以便进行后续的文本分析和挖掘工作。简单说，预处理就是把文本整理成一种格式，方便后面用计算机程序来分析。

3.4 第二分枝——分词（Tokenization）

分词（Tokenization）是文本处理中的一项基础任务，指的是将文本切分成许多小部分，这些小部分被称为“标记”（tokens）。在不同的语境中，一个标记可以是一个字符、一个音节、一个词、一个句子、一个段落，甚至是一个章节等。

        字符：最小的标记单元，如英文中的a、b、c或汉字。字符的标准定义可以参考Unicode标准附件#29，这是一个国际标准，为世界上大多数的书写系统提供了一个唯一的编号。
        音节：语言中的基本发音单位。
        词：通常是指基于字形的词，也就是在书写中以空格或者标点符号分隔开的单元。
        句子：一个完整的思想或陈述单位，通常以句号、问号或感叹号结束。
        段落和章节：文本的更大的结构单元，通常包含多个句子。

对于不使用空格分隔单词的语言（如中文、泰语、高棉语，甚至部分阿拉伯语等），分词尤其具有挑战性，因为必须通过上下文来确定单词的边界。

在处理文本时，“层”的概念非常重要。如果在某一层（比如分词）遇到问题，可以利用上一层的信息（比如句子结构）来帮助解决。分词是文本处理的基础，如果在这一步出现错误，可能会影响到后续的所有分析工作。因此，准确的分词对于整个文本分析来说至关重要。

3.5 第二分枝——词干提取（Stemming）和词形还原（Lemmatization）

词干提取（Stemming）和词形还原（Lemmatization）都是文本预处理中常用的技术，用于减少单词的变形形式，使其归一化到一个基本形式。

词干提取：是通过去掉单词末尾的词尾来实现的。例如，法语单词 porteront 的词干是 port 。这个过程是自动的，有时可能不会考虑单词的实际用法和语法，因此得到的词干可能不是一个真正的单词。

词形还原：则是将单词转化为其标准的词典形式，也就是词的原形。比如，法语单词porteront 的原形或词元是 porter （动词的不定式形式）。词形还原通常需要词汇和语法的知识，这个过程会考虑单词的具体用法，所以比词干提取更为精确。

简单来说，词干提取更加粗糙，通常只是简单地去掉单词后面的一部分；而词形还原更加细致，会尝试找到单词的正确原形。因此，词形还原通常比词干提取更为准确，但也更复杂。在某些应用中，比如搜索引擎，词干提取可能就足够了，因为它运行快速并且相对简单。而在需要高精度的语言处理任务中，比如语义分析，词形还原会更为合适。

3.6 停用词

停用词（Stop-words）是指在文本处理中通常被排除的那些词，因为它们在大多数情况下不携带主题信息或重要意义。停用词的列表是依赖于语言的，因为不同语言中使用频率高、意义相对空泛的词汇不同。

在英语中，停用词包括许多介词（如above、between）、连词（如and、“but”）、代词（如“he”、“they”）、助动词（如“can”、“will”）、冠词（如the”、“an”）等。这些词在句子中充当语法结构的作用，但它们自身不包含具体的内容信息。

尽管停用词在主题检索或关键词提取时经常被忽略，但在某些文本处理或语言理解的场景中，移除停用词可能会改变句子的意思或者影响信息的完整性。例如，在情感分析或者语言模型中，停用词的存在对句子的语气和意图可能有重要影响。因此，在决定是否移除停用词时，需要根据具体的应用场景和目的谨慎考虑。

4. 语言模型搭建 —— 基于统计的语言模型

语言模型是指对每个词序列的概率的建模。特别地，它关注于下一个词的概率，即给定一系列前面的词之后，预测下一个词出现的概率： $P(w_n | w_1, ..., w_{n-1})$

4.1 搭配（Collocations）

搭配（Collocations）指的是在语言中经常一起出现的词语组合，这些组合在统计上具有显著性。它们可以是复合名词（如disk drive硬盘驱动器）、短语动词（如make up化妆或编造）或固定短语（如bacon and eggs 培根加鸡蛋）。

搭配可以通过点互信息（pointwise mutual information, PMI）来评估，这是一个衡量两个变量之间相关性强度的统计量。PMI的公式如下：

$I(x, y) = \log_2 \frac{P(xy)}{P(x)P(y)}$

这里的 $P(xy)$ 表示两个词 $x$ 和 $y$ 一起出现的概率，而 $P(x)$ 和 $P(y)$ 分别表示词 $x$ 和词 $y$ 各自出现的概率。PMI的值越高，表示这两个词一起出现的频率超过了随机组合的频率，因此它们构成了一个强搭配。

搭配的特点包括：

        非组合性：某些搭配的意思不能通过组成它们的单词的字面意思来理解，比如 red herring （红鲱鱼，实际意为转移注意力的事物）。
        不可替代性：在搭配中的词通常不能被同义词替换，例如用 yellow wine 来替换 white wine （白葡萄酒）就显得不合适。
        不可修改性：一些搭配不能随意更改其中的词，比如将 it rains cats and dogs （下倾盆大雨）改成“it rains small cats and bad dogs”就不正确。
        不可直译性：一些搭配不能直接翻译到其他语言中保持原有的意义，比如将英文的“It's raining cats and dogs”直译为法语的“il pleut des chats et des chiens”（下猫下狗），在法语中并不表示“下倾盆大雨”的意思。

需要注意的是，搭配不应该与术语表达式（terminological expressions）混淆，术语通常是指专业领域中的固定词汇，而搭配更多指的是日常语言中自然形成的词组。

4.2 语言模型的概念LM

语言模型（Language Model, LM）是用来计算一个句子出现概率的模型。它在自然语言处理（NLP）中扮演着重要的角色，特别是在机器翻译、语音识别、拼写纠错等领域。语言模型的基本思想是根据语言出现的规律来预测下一个词或者给定一个句子的概率。

4.2.1 词汇表（Vocabulary）

词汇表是语言模型中所有可能出现单词的集合，用 $V$ 表示。例如，如果我们有一个非常简单的词汇表，里面只包含“eat”、“pizza”和“drink”，那么我们可以表示为 $V = \{"eat", "pizza", "drink"\}$ 。

4.2.2 相对频率和最大似然估计（MLE Training）

最大似然估计（Maximum Likelihood Estimation, MLE）是一种用来训练语言模型的方法，通过计算词语在给定语料库中出现的相对频率来估计概率。比如，要计算句子“eat pizza”出现的概率，我们可以用“eat pizza”这个词组在语料库中出现的次数除以“eat”出现的次数，这样就可以得到条件概率 $P(\text{"pizza"}|\text{"eat"})$ 。

相对频率的计算公式通常如下：

$P(w_n|w_{n-1}) = \frac{Count(w_{n-1}, w_n)}{Count(w_{n-1})}$

这里， $w_n$ 是当前的词， $w_{n-1}$ 是前一个词， $Count(w_{n-1}, w_n)$ 是两个词连在一起出现的次数，而 $Count(w_{n-1})$ 是 $w_{n-1}$ 单独出现的次数。

4.2.3 例子：比较“eat pizza”和“drink pizza”

在最大似然估计框架下，如果我们要比较“eat pizza”（吃比萨）和“drink pizza”（喝比萨）两个短语的概率，我们会查看这两个短语在语料库中的出现频率。直观上，因为“eat pizza”在现实生活中的语境中出现得更频繁，所以 $P(\text{"eat pizza"})$ 应该大于 $P(\text{"drink pizza"})$ 。这就是说，在我们的语言模型中，“eat pizza”的概率高于“drink pizza”，这与我们的直觉和实际使用情况相匹配。

4.3 N-gram模型(N元组)

n-gram模型是一种基础的语言模型，它假设一个词出现的概率仅依赖于它前面的 $n-1$ 个词。这个模型通过统计各种词序列在训练数据中出现的频率来估计概率,。分类通常有Unigram,Bigram,Trigram。

4.3.1 一元语言模型Unigram language Models

一元语言模型（Unigram Language Models）是最简单的语言模型之一，它假设句中每个词的出现是独立的（即，它不考虑词与词之间的顺序或依赖关系）。这种模型的关键在于估算句子中每个单词出现的概率，并将这些概率相乘以得到整个句子出现的概率。

4.3.1.1 估算概率

通过iid词或短语的概率估算某句话的概率：P(s) = P(w1)P(w2)P(w3).......P(wn)

在一元模型中，一个句子 $s$ 的概率 $P(s)$ 可以通过句子中所有单词概率的乘积来估算。如果句子由个 $n$ 词组成： $w_1, w_2, ..., w_n$ ，那么句子的概率可以表示为：

$P(s) = P(w_1)P(w_2)...P(w_n)$

这里， $P(w_i)$ 是单词 $w_i$ 出现的概率，可以通过该单词在语料库中出现的频率除以总单词数量来估计。

4.3.1.2 out-of-vocabulary OOV

在实际应用中，我们经常会遇到一些在训练语料库中未出现过的词，这些词被称为词汇表外（Out-of-Vocabulary，简称OOV）词。因为我们无法直接从训练数据中估计这些词的概率，它们会给语言模型的使用带来挑战。

4.3.1.3 add- $\alpha$ smoothing加 $\alpha$ 平滑

为了解决OOV问题并改进概率估计，一种常用的技术是加平滑（Additive Smoothing），通常也称为拉普拉斯平滑（Laplace Smoothing）。加平滑的基本思想是给所有可能的单词（包括那些在训练集中未出现的单词）一个小的非零概率，以此来避免计算概率时出现零概率的情况。

假设我们的词汇表大小为 $V$ ，加平滑公式调整了单词 $w$ 的概率计算方法，变为：

$P(w) = \frac{Count(w) + \alpha}{N + \alpha \times V}$

这里， $Count(w)$ 是单词 $w$ 在训练集中出现的次数， $N$ 是训练集中总单词数， $\alpha$ 是平滑参数（通常取1）， $V$ 是词汇表的大小。通过这种方法，即使是在训练集中从未出现过的单词，其概率也不会是零，从而可以有效处理OOV问题，并使概率估计更加平滑和鲁棒。

4.3.2 二元语言模型Unigram language Models

二元语言模型（Bigram Language Models）是在自然语言处理中常用的一种模型，它考虑了词与词之间的顺序关系。不同于一元模型（Unigram Model）只考虑单个词出现的概率，二元模型通过使用条件概率来考虑两个连续词的出现概率，从而更好地捕捉语言的结构。

4.3.2.1 估算概率

在二元语言模型中，一个句子 $s$ 的概率是通过计算句子中每对连续单词出现的条件概率的乘积来估算的。用数学表示为：

$P(s) = P(w_1|<s>)P(w_2|w_1)...P(w_n|w_{n-1})P(</s>|w_n)$

这里， $P(w_i|w_{i-1})$ 表示在前一个词是 $w_{i-1}$ 的条件下，词 $w_i$ 出现的条件概率。

4.3.2.2 推导过程

二元模型的概率计算可以通过链式法则来推导。链式法则是概率论中的一个重要原理，它允许我们将联合概率分解为一系列条件概率的乘积。对于句子 $s$ ，我们可以表示为：

$P(s) = P(w_1|<s>)P(w_2|<s>,w_1)...P(wn|<s>,w_1,...,w_{n-1})$

但在二元模型中，我们做了一个条件独立的假设，即每个词的出现只与它前面的一个词有关。因此，我们可以简化为：

$P(s) = P(w_1|<s>)P(w_2|w_1)...P(wn|w_{n-1})$

4.3.2.3 稀疏性问题

稀疏性问题是指在实际语料库中，许多词对组合可能从未出现过，或者出现的非常少，这导致了模型对这些词对的概率估计不准确或无法进行。这个问题在二元模型中尤为突出，因为条件概率的计算需要两个词的组合在训练数据中有足够的出现次数。

4.3.2.4 回退Back-off

为了解决稀疏性问题，可以使用回退（Back-off）技术。回退模型在计算条件概率时，如果当前词对的数据稀疏或不存在，就会退回到更简单的模型（如一元模型）来估计概率。具体来说，如果 $P(w_2|w_1)$ 的估计不可靠或无法计算，我们可以用 $P(w_2)$ 来近似，并通过一个平滑参数来调整这两者的权重，公式如下：

$P_{\text{backoff}}(w_2|w_1) = \lambda P(w_2|w_1) + (1-\lambda)P(w_2)$

这里， $\lambda$ 是一个介于 0 和 1 之间的参数，用于调整二元概率和一元概率的相对重要性。通过这种方式，回退技术使得模型在面对稀疏数据时更加鲁棒，能够给出更加合理的概率估计。

4.3.3 三元语言模型Unigram language Models

三元语言模型（Trigram Language Models）是自然语言处理（NLP）中的一种统计模型，它考虑了句子中每个词与其前面两个词的关系。这种模型比一元（Unigram）和二元（Bigram）模型能更好地捕捉语言的上下文信息，因为它考虑了更长的词的序列依赖。

4.3.3.1 概率计算

在三元模型中，一个句子 $s$ 的概率计算公式可以表示为连续词对的条件概率的乘积：

$P(s) = P(w_1|<s>)P(w_2|<s>, w_1) \prod_{i=3}^{n} P(w_i|w_{i-2}, w_{i-1})$

这里， $P(w_i|w_{i-2}, w_{i-1})$ 表示给定前两个词 $w_{i-2}$ 和 $w_{i-1}$ 的情况下，词 $w_i$ 出现的条件概率。

4.3.3.2 训练方式

三元模型的训练通常使用最大似然估计（MLE）方法，它根据训练语料中的词序列出现的频率来估计条件概率：

$P(w_i|w_{i-2}, w_{i-1}) = \frac{Count(w_{i-2}, w_{i-1}, w_i)}{Count(w_{i-2}, w_{i-1})}$

这里， $Count(w_{i-2}, w_{i-1}, w_i)$ 表示三个词 $w_{i-2}\), \(w_{i-1}$ , 和 $w_i$ 作为一个序列连续出现的次数，而 $Count(w_{i-2}, w_{i-1})$ 是前两个词作为序列出现的次数。

4.3.3.3 Back-off（回退）技术

由于数据稀疏性问题在三元模型中更为严重（因为需要三个词的组合出现在训练集中），所以经常使用回退（Back-off）技术来解决。当特定的三元组在训练数据中没有出现或出现次数很少时，回退技术允许模型“回退”到二元或一元模型来估计条件概率。

具体来说，如果 $P(w_i|w_{i-2}, w_{i-1})$ 的可靠估计不可行，模型可以尝试使用 $P(w_i|w_{i-1})$，即退回到二元模型的估计；如果二元模型的估计也不可靠，甚至可以进一步回退到一元模型 $P(w_i)$。在实践中，可以通过设定一系列阈值来确定何时进行回退，以及如何结合不同模型的估计来得到最终的概率估计，这通常涉及到对不同层次模型的概率估计进行加权或调整。通过这种方法，即使在面对数据稀疏问题时，三元模型也能提供较为准确的概率估计，从而更好地捕捉语言的上下文信息。

4.3.4 N-gram模型(N元组)

对于一个特定的词序列，其概率可以用以下公式进行估计：

这个概率可以通过最大似然估计（Maximum Likelihood Estimation, MLE）来估算，即通过以下公式计算给定前面所有词序列时，下一个词出现的概率：

$P_{MLE}(w_n | w_1, ..., w_{n-1}) = \frac{\#(w_1 ... w_n)}{\#(w_1 ... w_{n-1})}$

$P(w_n | w_{n-1}, w_{n-2}, ..., w_{n-N+1}) = \frac{Count(w_{n-N+1}, ..., w_{n-1}, w_n)}{Count(w_{n-N+1}, ..., w_{n-1})}$

这里，表示序列 $w_1 ... w_n$ 在数据中出现的次数，而 $\#(w_1 ... w_{n-1})$ 表示序列 $w_1 ... w_{n-1}$ 出现的次数。这种模型被称为n-gram模型。换而言之，其中， $Count(w_{n-N+1}, ..., w_{n-1}, w_n)$ 表示序列 $w_{n-N+1}, ..., w_{n-1}, w_n$ 在数据中出现的次数，而 $Count(w_{n-N+1}, ..., w_{n-1})$ 表示序列 $w_{n-N+1}, ..., w_{n-1}$ 出现的次数。

这个计算方式是用来估算在给定前面的词序列 $w_{n-N+1}, ..., w_{n-1}$ 的条件下，下一个词 $w_n$ 出现的条件概率。也就是说，它反映了所有这些词按照特定顺序同时出现的频率相对于它们的前缀（不包括最后一个词）出现的频率。这并不是这些词独立出现的概率相乘，而是它们作为一个整体序列出现的实际情况在数据集中的观察频率。

具体来说， $P(w_n | w_{n-1}, ..., w_{n-N+1})$ 代表了在观察到序列 $w_{n-N+1}, ..., w_{n-1}$ 之后，词 $w_n$ 紧接着出现的概率。这是一个条件概率，因为它是在已知前面的词序列的条件下计算的。这里的关键点是，我们是基于特定的上下文（即前面的词序列）来预测下一个词的出现概率，而不是单纯地考虑这些词各自独立出现的概率。

例如，在一个3-gram模型中，如果我们计算 sleeps 在“the cat”之后出现的概率，我们实际上是在问：在我们观察到‘the cat’这个序列的情况下，下一个词是‘sleeps’的概率是多少？这个概率是通过将 the cat sleeps 这个序列在数据中出现的次数除以“the cat”这个序列出现的次数来估计的。这反映了在给定“the cat”作为上下文时， sleeps 作为下一个词出现的频率。

4.3.5 稀疏性sparcity问题

稀疏性是指在实际数据集中，许多可能的词序列从未出现过，导致这些词序列的概率被估计为零。这种情况会严重影响模型的性能和泛化能力，因为它不能合理地处理未见过的词序列。

n-gram模型的主要问题是稀疏性（sparsity），即很多词序列在实际数据中可能从未出现过，导致其概率估计为零，这会影响模型的性能和泛化能力。

4.3.6 线性插值解决方案（Linear Interpolation）

为了解决稀疏性问题，可以采用线性插值（Linear Interpolation）的方法，该方法通过结合不同长度的n-gram模型来估计词序列的概率。具体来说，一个词的概率不仅由其在长序列中的出现概率决定，也由它在更短的序列中的出现概率共同决定。公式如下：

$P_{interp}(w_n | w_{n-1}, ..., w_{n-N+1}) = \lambda_1 P(w_n | w_{n-1}, ..., w_{n-N+1}) + \lambda_2 P(w_n | w_{n-1}, ..., w_{n-N+2}) + ... + \lambda_N P(w_n)$

同等公式：

$P_{lin}(w_n | w_1, ..., w_{n-1}) = \lambda_1P(w_n) + \lambda_2P(w_n | w_{n-1}) + \lambda_3P(w_n | w_{n-2}, w_{n-1}) + ...$

其中， $\lambda_1, \lambda_2, ..., \lambda_N$ 是权重系数，用于平衡不同长度n-gram模型的贡献， $\lambda_i$ 是权重系数，用于平衡不同长度n-gram模型的贡献，且所有的 $\lambda_i$ 之和等于1 $\sum_{i} \lambda_i = 1$ 。这些权重可以通过数据学习得到，且（ $k$ 考虑的最大n-gram长度）远小于 $n$ （整个词序列的长度），以避免模型复杂度过高，以确保模型能够在保持合理复杂度的同时，更有效地处理数据稀疏性问题。

通过线性插值，模型不仅考虑了长序列中的上下文信息，也利用了短序列中的信息，从而在未见过的词序列上提供了更平滑、更合理的概率估计，显著提高了模型的泛化能力。

4.4 朴素贝叶斯文本分类

4.4.1 文本分类问题

输入是：

5. 基于向量的语言模型

判别式的模型

5.1 特征向量

6.基于对数线性模型

7. 带有隐变量的神经网络模型

8. 结构预测问题——基于序列的模型

8.1 序列标注

8.1.1 词性标注问题

输入：一个句子。

输出：词性标签。

由周围的词性来确定这个词性

8.2 隐马尔可夫模型（Hidden Markov Models ,HMM）生成式模型

隐马尔可夫模型（HMM）是一种统计模型，用于描述一个系统的状态序列，其中每个状态不是直接可见的，但通过观察可见的事件序列间接推断。这里给出的是一个可见的马尔可夫模型（也称为马尔可夫链）的简化说明，不涉及隐状态和可观察输出之间的关系，而是直接描述状态序列本身的性质。

8.2.1 马尔可夫链

马尔可夫链：设 $X = (X_1, ..., X_T)$ 是一个随机变量序列，这些随机变量的取值在有限空间 $S = \{s_1, ..., s_N\}$ 中。

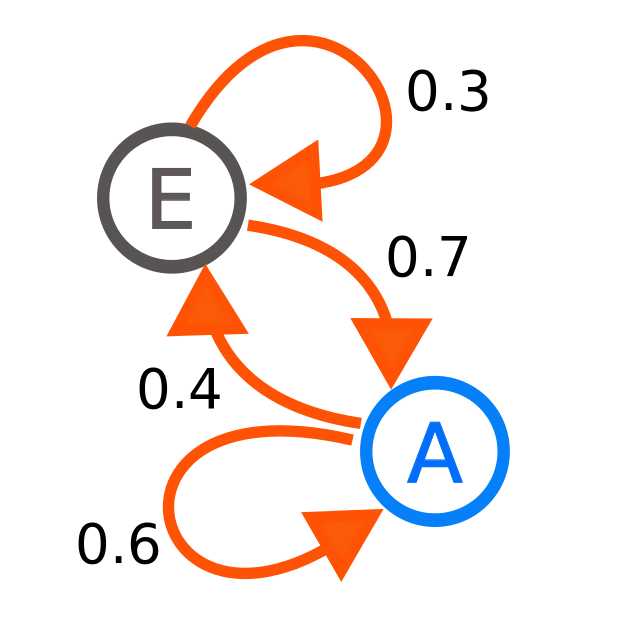
8.2.2 马尔可夫链的特性

8.2.2.1 有限视野性（the limited horizon）

当前状态的下一个状态的概率仅依赖于当前状态，而不依赖于之前的状态序列。数学上表示为 $P(X_{t+1} = s_k | X_1, ..., X_t) = P(X_{t+1} = s_k | X_t)$

8.2.2.2 平稳性（the stationarity）

任意时刻 $t$ 的转移概率与时间无关，即转移概率是恒定的。表示为 $P(X_{t+1} = s_k | X_t) = P(X_2 = s_k | X_1)$ 。

平稳性（stationarity）在统计和时间序列分析中是一个重要概念。当我们说一个过程是平稳的，意味着这个过程的统计属性（如平均值、方差和自相关性）不随时间改变。简而言之，平稳性指的是无论我们在时间序列的哪个点开始观察，数据的行为和性质都是相同的。

“任意时刻的转移概率与时间无关，即转移概率是恒定的”，这是指在马尔科夫链中，系统从一个状态转移到另一个状态的概率不随时间改变。这意味着，无论我们在过程中的哪个时间点观察，转移概率都是相同的。

这个概念在很多领域都非常重要，如信号处理、经济学、物理学等。它允许我们使用过去的数据来预测未来的行为，因为过程的统计性质是恒定的。在实际应用中，很多时间序列数据可能不是严格平稳的，因此需要通过某些方法（如差分、转换等）使其尽可能地接近平稳，以便于分析和预测。

8.2.2.3 状态和转移概率

在这样的模型中， $S$ 是状态的集合， $a_{ij} = P(X_{t+1} = s_j | X_t = s_i)$ 是从状态 $s_i$ 转移到状态 $s_j$ 的概率，称为转移概率，而整个转移概率的集合构成一个随机矩阵（stochastic matrix）。

8.2.2.4 初始状态概率

初始状态 $s_i$ 的概率为 $\pi_i = P(X_1 = s_i)$ ，所有初始状态概率的和为1，即 $\sum \pi_i = 1$ 。

8.2.2.5 状态序列的概率

一个特定状态序列 $X$ 出现的概率可以通过初始状态的概率和状态转移概率的乘积来计算，即 $P(X_1, ..., X_T) = \pi_{X_1} \prod_{t=1}^{T-1} a_{X_t X_{t+1}}$

8.2.2.6 可见马尔可夫模型

这里描述的是一个可见马尔可夫模型，因为它直接处理状态序列，而不涉及观察序列和状态序列之间的隐含关系。

简而言之，马尔可夫链是一种数学模型，用于描述一个过程，其中下一个状态的发生仅依赖于当前状态，而与过去的状态无关。这种性质使得马尔可夫链成为分析各种序列数据（如语言处理、生物信息学和金融市场分析等领域）的有力工具。

8.4.3 第二分枝：词性标注的应用——隐马尔可夫模型

隐马尔可夫模型（Hidden Markov Model，简称HMM）是一种统计模型，它用来描述一个含有隐含未知参数的马尔可夫过程。

在自然语言处理中，HMM常用于词性标注（part-of-speech tagging），即确定句子中每个单词的词性（名词、动词等）。

8.4.3.1 HMM和词性标注

8.4.3.1.1 隐马尔可夫模型（HMM）

在某些情况下，我们无法直接观察到状态序列，只能观察到一些与状态序列相关的输出。这些输出被认为是状态的随机函数。在这种情况下，我们使用隐马尔可夫模型来描述这一过程。
在自然语言处理中，句子中的词 $w_i$ 可以看作观测序列，而每个词对应的词性 $t_i$ 则是隐藏的状态序列。

8.4.3.1.2 学习

我们通过在已标注的训练语料库上进行学习来估计模型参数，即状态转移概率和观测概率。

8.4.3.1.3. 参数估计

        训练语料库中，某个词 $w_\ell$ （词汇表中的词）的出现次数记为 $\#(w_\ell)$ 。
        某个词性 $t_j$ （可用的标签或词性）的出现次数记为 $\#(t_j)$ 。
        词性 $t_j$ 后面跟着词性 $t_k$ 的次数记为 $\#(t_j, t_k)$ ，这是状态转移概率的估计。
        词 $w_\ell$ 被标注为词性 $t_j$ 的次数记为 $\#(w_\ell : t_j)$ ，这是观测概率的估计。

8.4.3.2 概率估计

在隐马尔可夫模型（Hidden Markov Model, HMM）中，我们通常对模型参数进行最大似然估计（Maximum Likelihood, MV）来找出最有可能的参数值。

8.4.3.2.1 状态转移概率的估计

$\hat{P}(t_k | t_j)$ 表示在给定前一个词性 $t_j$ 的情况下，下一个词性是 $t_k$ 的概率。
这个概率是通过计算词性 $t_j$ 后面紧跟着词性 $t_k$ 的次数 $\#(t_j, t_k)$ 与词性 $t_j$ 总共出现的次数 $\#(t_j)$ 的比值得到的。

8.4.3.2.2 观测概率的估计

$\hat{P}(w_t | t_j)$ 表示在给定词性 $t_j$ 的情况下，观测到单词 $w_\ell$ 的概率。
这个概率是通过计算单词 $w_\ell$ 被标记为词性 $t_j$ 的次数 $\#(w_\ell : t_j)$ 与词性 $t_j$ 总共出现的次数 $\#(t_j)$ 的比值得到的。

8.4.3.2.3 最优词性序列的求解

        要找到最优的词性序列，我们使用 argmax 函数来选择使得整个句子的概率最大化的词性序列 $\hat{t}_{1,n}$ 。
        这个过程通过计算给定词性序列下，观测到整个单词序列 $w_1, w_2, ..., w_n$ 的概率的乘积，并选择这个乘积最大的词性序列来实现。
        公式可以表示为： $\hat{t}_{1,n} = \arg \max_{t_1, ..., t_n} \prod_{i=1}^{n} \hat{P}(w_i | t_i) \hat{P}(t_i | t_{i-1})$ 。

8.4.3.2.4 问题 - 指数复杂度

问题在于，对于一个长句子来说，计算所有可能的词性序列的概率并找出最大的那个会有指数级的时间复杂度。
这意味着随着句子长度的增加，所需要计算的可能序列数量呈指数增长，这使得直接计算变得不可行。

为了解决这个问题，通常会使用Viterbi算法。Viterbi算法是一种动态规划算法，它通过只保留到达每个状态的最高概率路径，避免了对所有可能路径的显式枚举，从而大大减少了计算量。这使得在实践中找到最优词性序列变得可行。

8.4.3.3 举例

假设我们有一句话“他看书”，我们要用HMM进行词性标注。我们的标签集合是{名词(N)，动词(V)}。在训练语料库中，我们可能有以下统计信息：

        他这个词作为名词出现了100次 $\#("ta": N) = 100$ 。
        名词后面跟动词的情况出现了50次 $\#(N, V) = 50$ 。
        看这个词作为动词出现了80次 $\#("kan": V) = 80$ 。

使用这些统计信息，我们可以估计转移概率和观测概率，然后使用Viterbi算法等方法来找出最有可能的标签序列。在这个例子中，最终我们可能得到的标注是“他(N) 看(V) 书(N)”。

首先，我们定义一些概率：

初始概率：指的是句子第一个词性出现的概率。这通常是基于训练语料统计得到的，但这里我们没有具体的初始概率，所以可能会假设每个词性出现的概率是等可能的，或者基于语料库中的分布。

转移概率：指的是一个词性后跟另一个词性的概率。在这个例子中，我们只有“名词后面跟动词”的转移概率，即 $P(V|N) = \frac{\#(N,V)}{\#(N)}$ 。但我们没有给出其他转移概率，比如 $P(N|N)$ 或 $P(V|V)$ 。这些通常需要从语料库中获取。

观测概率：指的是给定一个词性时，观测到某个特定单词的概率。根据给出的信息，我们有：
$P("ta"|N) = \frac{\#("ta":N)}{\#(N)}$ $P("kan"|V) = \frac{\#("kan":V)}{\#(V)}$

现在，让我们使用Viterbi算法来为句子他看书找到最有可能的词性序列。为了简化这个例子，我们假设除了给定的概率外，其他的转移概率和观测概率都是0.5（这只是为了示例，实际中这些概率应由语料库中的数据得出）。

假设的概率如下：

         $P(N|N) = 0.5, P(V|N) = 0.5$
         $P(N|V) = 0.5, P(V|V) = 0.5$
         $P("ta"|N) = \frac{100}{\#(N)}, P("kan"|V) = \frac{80}{\#(V)}$
        假设 $P("shu"|N) = 0.5$

Viterbi算法是一种动态规划算法，广泛用于隐马尔可夫模型（HMM）中计算最可能的状态序列——在自然语言处理中，这通常是指最可能的词性标注序列。现在，让我解释如何使用Viterbi算法为句子“他看书”找到最有可能的词性序列。

我们会设定一些概率，并使用这些概率来计算每个单词最可能的词性。在这个简化的例子中，我们还假设未给出的转移概率和发射概率（观测概率）都是0.5。

以下是使用Viterbi算法的步骤：

a.初始化：
我们先为句子中的第一个词“他”设定一个词性，假设它是名词（N）。这是初始化步骤，通常会基于单词的发射概率进行。

b.迭代：
        接着我们考虑第二个词“看”。我们计算两种情况的概率：
        如果“他”是名词，那么“看”是动词（V）的概率。
        如果“他”是动词，那么“看”还是动词的概率。
        我们选择上述两种情况中概率较高的一个，作为当前最优的选择。因为我们假设“他”是名词，所以我们会选择“看”作为动词的概率。

c.下一个词：
        对于第三个词“书”，我们再次计算两种情况的概率：
        如果“看”是动词，那么“书”是名词的概率。
        如果“看”是名词，那么“书”还是名词的概率。
        同样的，我们选择概率较高的情况。

在每一步，我们不仅考虑到了发射概率（一个特定词性产生某个词的概率），还考虑到了转移概率（一个词性转移到另一个词性的概率）。Viterbi算法会在每个步骤存储当前的最优路径（即到目前为止最可能的词性序列）和相应的概率。通过这种方式，我们可以有效地处理整个句子，并最终得出整个句子的最可能词性序列。

在实际的自然语言处理任务中，这些概率会通过大量的语言数据进行学习和训练，以确保模型可以准确地反映自然语言的统计特性。这个例子中的概率和简化的假设只是为了演示算法的计算过程。

8.4.3.4 三元标记器

三元标记器（Trigram Tagger）是自然语言处理（NLP）中的一种工具，用于词性标注（Part-of-Speech Tagging，简称POS Tagging）。词性标注的目的是自动识别文本中每个单词的词性（如名词、动词、形容词等）。三元标记器在执行这一任务时，会考虑一个单词及其前面两个单词的上下文信息，基于这三个单词（即“三元”）来预测当前单词的词性。

8.4.3.4.1 工作原理

三元标记器根据前两个单词的词性来预测第三个单词的词性。它使用了称为三元模型（Trigram Model）的概念，这是一种统计语言模型，考虑连续三个项目（在此上下文中是词性）的序列概率。模型会尝试计算某个词性出现在特定两个词性序列后面的概率。

例如，如果我们有句子“猫喜欢吃鱼”，三元标记器会考虑“猫喜欢”（名词+动词）这个词性序列，来预测“吃”这个词的最可能词性（在这个例子中是动词）。

8.4.3.4.2 训练

三元标记器的训练通常使用最大似然估计（MLE），这涉及到基于训练语料库中的词性序列出现频率来计算概率。具体地，它会计算每种三元词性序列（前两个词的词性和当前词的词性）在训练数据中出现的概率。

8.4.3.4.3 Backoff

在实际应用中，三元标记器可能会遇到数据稀疏性问题，即某些三元词性序列在训练集中未出现过或出现频率极低，使得概率估计不准确或不可靠。为了解决这个问题，通常会使用Backoff技术。如果三元模型不能提供可靠的预测（比如因为某个特定的三元序列在训练数据中没有出现），标记器会退回到二元模型（考虑当前单词和它前面一个单词的词性），甚至一元模型（只考虑当前单词的词性）。通过这种方式，Backoff技术提高了模型的覆盖范围和灵活性，确保即使在面对未见过的单词序列时也能做出合理的词性预测。

8.4.3.5 多元标记器

隐马尔可夫模型（HMM）基本上是一种双元标记器，它在自然语言处理中常用于词性标注。例如，在法语句子 la jeune fille la porte 中，很难仅从 la 来判断“porte”是名词还是动词，因为“la”既可以作为冠词也可以作为代词，这导致了歧义。

Church在1988年描述了一种三元标记器。在三元标记器中，我们可以计算一个长度为n的词序列 $w_{1,n}$ 有标记序列 $t_{1,n}$ 的概率。这个概率可以通过递归地使用以下公式来计算：

$p(w_{1,n}, t_{1,n}) := p(t_n | t_{n-2} t_{n-1}) \times p(w_n | t_n) \times p(w_{1,n-1}, t_{1,n-1})$

        这里：
         $p(t_n | t_{n-2} t_{n-1})$ 是在给定前两个词性的条件下，当前词性出现的条件概率。
         $p(w_n | t_n)$ 是在给定当前词性的条件下，当前单词出现的条件概率。
         $p(w_{1,n-1}, t_{1,n-1})$ 是前n-1个单词和其对应词性序列出现的概率。

我们可以根据最大似然（MV）原则来估计 $p(t_n | t_{n-2} t_{n-1})$ ，方法是计算三元组 $t_{n-2} t_{n-1} t_n$ 出现的频率除以双元组 $t_{n-2} t_{n-1}$ 出现的频率。

然而，存在一个问题：这些概率可能会非常低（如果三元组在训练语料中没有出现，甚至可能是零）。

这会导致模型在处理未见过的词组合时性能下降，因为模型无法从未见过的组合中学习到信息。

为了克服这个问题，通常会使用平滑技术，比如拉普拉斯平滑或古德-图灵估计，来调整那些低概率的数值，确保模型对于未见过的数据也有一定的处理能力。

9 结构预测问题——基于树状结构的模型

9.1 树的基本概念

9.1.1 第二分枝——句法分析

句法分析，也称为语法分析，是自然语言处理（NLP）中的一项核心任务，旨在理解和解析句子的语法结构。输入是自然语言文本，输出通常是一个成分句法树，该树描绘了句子的层级语法结构。

成分句法树：这种树状结构展示了句子从整体到局部的分解，包括句子（S）、短语（比如名词短语NP、动词短语VP）以及词性（如名词N、动词V、形容词A等）。每个节点表示语言的一个构成成分，根节点代表整个句子，叶节点代表句子中的词汇。

9.1.2 树结构的序列化

树结构的序列化是将树形结构转换为线性序列的过程，目的是为了更便于存储、传输和处理。常见的序列化方法包括：

括号表示法（Bracketed Notation）：使用括号和标签来表示树的层级结构，例如“(S (NP ...) (VP ...))”。
XML或JSON表示：利用这些标记语言的结构化特点来描述树，使得树结构在不同的平台和语言之间可以轻松共享和处理。

9.1.3 二叉化

二叉化是句法分析中的一种技术，用于将具有多个分支的树结构转化为只有两个分支的二叉树。这样做的目的是简化句法分析和处理过程，因为二叉树比多叉树更易于管理和操作。二叉化通常有三种方法：

9.1.3.1 左二叉化

在左二叉化中，每个节点的左子节点保留为原树结构中的第一个子节点，而其他子节点被递归地合并到右子节点中。这种方法倾向于保留左侧的树结构。

9.1.3.2 右二叉化

右二叉化正好相反，它保留每个节点的最后一个子节点作为右子节点，而其他子节点被递归地合并到左子节点中。这种方法倾向于保留右侧的树结构。

9.1.3.3 头二叉化

头二叉化是一种更为复杂的二叉化方法，它根据“头”（通常是最重要的子节点，如主谓宾结构中的谓语）的位置来决定如何进行二叉化。如果“头”在左边，则采取类似左二叉化的方式；如果“头”在右边，则采用类似右二叉化的方式。头二叉化的目的是保留语言学中的“头”驱动特性，使得二叉化后的树更贴近自然语言的语法特征。

二叉化处理后，虽然树的形态改变，但通过适当的转换规则，可以确保原始的语法信息不丢失，从而在简化句法分析结构的同时，保持语言学的精确性。

9.2 TreeTagger

TreeTagger是一种用于自然语言处理的工具，它使用二叉决策树来确定给定前两个词性时第三个词性的概率，即 $p(t_n | t_{n-2} t_{n-1})$ 。下面用中文解释TreeTagger是如何工作的：

9.2.1 二叉决策树

TreeTagger使用一棵决策树来决定词性标注的概率。决策树是一种机器学习模型，它通过一系列的问题来导向决策。在这个上下文中，这些问题是关于前一个词 $t_{n-1}$ 和前前一个词 $t_{n-2}$ 的词性。

9.2.2 概率决策示例

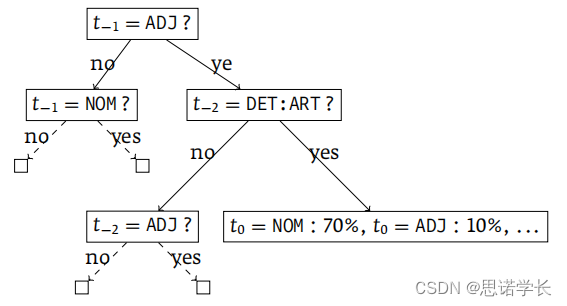
在决策树中，一个问题可能是：前一个词是形容词（ADJ）吗？。如果答案是“是”，则可能接着问“前前一个词是冠词（DET:ART）吗？”。

根据这些问题的答案，决策树将导向不同的概率决策。例如，如果路径是“是，是”，则当前词是名词（NOM）的概率可能是70%，是形容词的概率可能是10%，等等。

TreeTagger中使用的二叉决策树的一个例子。二叉决策树是通过一系列的是/否问题来预测目标变量的值，在这个情况下目标变量是词 $t_0$ 的词性。

图中这个过程可以用以下步骤来描述：

a. 首先，决策树询问前一个词的词性 $t_{-1}$ 是否是形容词（ADJ）。

如果答案是“否”，它接着询问前一个词是否是名词（NOM）。

如果答案是“是”，则继续询问前前一个词的词性 $t_{-2}$ 是否是冠词（DET:ART）。

b. 在第一个问题中，如果答案是“是”，则会根据 $t_{-2}$ 的词性来进行下一步的决策。
如果 $t_{-2}$ 不是冠词（DET:ART），则会继续询问 $t_{-2}$ 是否是形容词（ADJ）。
如果 $t_{-2}$ 是冠词（DET:ART），则根据这个信息给出 $t_0$ 的词性的概率分布，例如， $t_0$ 是名词（NOM）的概率是70%，是形容词（ADJ）的概率是10%，以此类推。

c. 在第一个问题中，如果答案是否，并且 $t_{-1}$ 也不是名词（NOM），那么就不再继续询问，因为已经有足够的信息来确定 $t_0$ 的词性。

d. 在第二个问题中，如果答案是否，并且 $t_{-2}$ 不是形容词（ADJ），则会给出一个默认的词性概率分布。

通过这样的一系列问题和决策，TreeTagger能够有效地预测未知词的词性。这个过程依赖于大量的训练数据来构建决策树，并且能够处理自然语言中的歧义和复杂性。通过使用不同的概率分布，决策树能够灵活地调整对不同上下文的反应，从而提高词性标注的准确性。

9.2.3 词典和后缀规则

TreeTagger拥有一个包含单词及其词性标注概率的词典，用于确定 $p(w_n | t_n)$ ，即在给定词性的情况下观测到某个特定单词的概率。如果词典中没有某个词，TreeTagger会使用正则表达式来匹配该词的后缀，从而推断其可能的词性。这种方法特别适用于处理未知单词或新词。

简而言之，TreeTagger是一种复杂的词性标注工具，它通过结合决策树和详尽的词典，以及对未知词的后缀分析，来提高词性标注的准确性。这种方法使得TreeTagger在各种语言和文本类型中都能够有效地标注词性，即使是在面对语料库中未出现过的单词时也是如此。

9.2.4 语法树

语法树是用来表示句子结构的树状图表，它展示了句子中各个部分之间的语法关系。在自然语言处理（NLP）中，语法分析器（又称句法分析器）是一种程序，用于计算句子的语法树。有时，一个句子可能对应多个语法树，这些树反映了句子可能具有的不同语义解释。

9.2.4.1 为什么会有多个语法树？

一个句子可能有多种语法结构，这取决于句中词语的多义性和语法结构的复杂性。比如，某些词语既可以作为名词也可以作为动词，这种词性的不确定性就可能导致生成多个不同的语法树。

9.2.4.2 如何解决多义性问题？

        为了解决这个问题，我们需要借助更高层次的分析，比如语义分析和语用分析：
        语义分析：试图理解句子的意义，确定词语的具体含义及其在句中的作用。
        语用分析：考虑语言使用的上下文，理解句子的含义及其可能的隐含意义。

9.2.4.3 图像解释

这张图展示了 le vendeur de serpents à sonnettes（响尾蛇的卖家）的两种不同的句法树。在自然语言处理中，句法分析器可以计算出一个句子的一个或多个句法树。不同的句法树可能对应不同的语义。为了消除歧义，我们需要依赖于更高层次的分析，比如语义分析和语用分析。

在这个例子中，左边的句法树将 de serpents（的蛇）看作是名词短语 le vendeur（卖家）的限定语，这意味着“卖家”和“蛇”之间有所属关系；而 à sonnettes（带铃铛的）则是限定 serpents（蛇），这意味着卖的是带铃铛的蛇。

右边的句法树则有所不同，它把 de serpents （的蛇）和 à sonnettes （带铃铛的）一起看作是对 le vendeur （卖家）的整体修饰，意味着这个卖家专门卖带铃铛的蛇。

简单来说，左边的句法树强调卖的是蛇，这些蛇恰好带有铃铛；而右边的句法树则表明卖家专门卖一种特定类型的蛇——带铃铛的蛇。通过上下文或者额外的语义信息，我们才能确定哪种理解是正确的。

9.2.4.4 示例解析

在句法分析中，每个字母的缩写代表了不同的语法成分。这些缩写是英文语法术语的缩写，即便是分析法语句子时也常用英文缩写。在您提供的句法树图片中，以下是每个缩写的含义：

        S：句子（Sentence）。这通常是整个句子结构的顶点。
        NP：名词短语（Noun Phrase）。它包含一个名词和它的修饰语，可以充当主语、宾语或者表语等。
        PP：介词短语（Prepositional Phrase）。由一个介词和它的宾语（通常是一个名词短语）组成。
        AT：冠词（Article）。在法语中，它通常指定代词le（男性单数定冠词）。
        NN：名词（Noun）。
        IN：介词（Preposition）。在法语中，de和à都是介词。

所以，当你看到这些术语时，它们代表了句子中的不同部分和功能。通过将句子分解成这些组成部分，句法分析器能够分析句子的结构，从而理解其意义和功能。

9.2.4.5 示例解析

考虑法语句子 la belle porte le voile 和 la vieille garde le lit ，这两个句子中都存在多义性，可能导致生成多个语法树。

9.2.4.5.1 示例1: la belle porte le voile

解释一：一个美丽的女人穿着面纱。
解释二：美丽的事物带来（或引起）隐藏或遮盖。

9.2.4.5.2 示例2:la vieille garde le lit

解释一：一个年老的女人看守着床铺。
解释二：老旧的守卫（或保护者）保持在床边。

在这些例子中，要确定每个句子的确切含义，就需要考虑到更多的上下文信息和对语言的深入理解。

总的来说，语法树是理解句子结构的有力工具，但要准确把握句子的全面含义，还需要结合语义和语用分析来解决多义性问题。

9.3 形式句法

9.3.1 上下文无关语法(CFG)

上下文无关语法（Context-Free Grammar，CFG）是一种用来描述一种自然语言或编程语言中句子的语法结构的规则集合。CFG主要由以下四个组成部分构成：

9.3.1.1 非终结符（N）

这些是语法的变量，代表了句子的结构组成部分，如短语或句子成分等。它们是产生式规则的左部，表示还可以被进一步替换的符号。

9.3.1.2 终结符（Σ）

这些是语法的基本符号，代表了句子中实际出现的词汇或字符。终结符构成了句子的最终输出，不再参与产生式规则的替换。

9.3.1.3 规则（R）

也称为产生式，是一系列的规则，指导如何从一个或多个非终结符生成终结符或其他非终结符的序列。规则定义了语言的结构，并指出了哪些符号序列是该语言中的有效句子。

9.3.1.4 开始符号（S）

CFG中的一个特殊非终结符，表示产生式规则的起点，用于推导出所有合法的句子。

一个CFG的例子可能如下所示：

        非终结符：N = {句子, 名词短语, 动词短语}
        终结符：Σ = {我, 鱼, 吃}
        规则：
        句子 → 名词短语动词短语
        名词短语 → 我 | 鱼
        动词短语 → 吃名词短语
        开始符号：句子

在这个例子中，我们可以用规则来生成句子，如“我吃鱼”，这个句子可以通过以下推导得到：

句子 → 名词短语动词短语 → 我动词短语 → 我吃名词短语 → 我吃鱼。

CFG被广泛用于编程语言的语法设计以及自然语言处理中的句法分析。在自然语言处理中，CFG可以被用来构建语法树，这些树展示了句子内部的层次结构。

9.3.2 随机上下文无关语法（Stochastic Context-Free Grammar, SCFG）

随机上下文无关文法（Stochastic Context-Free Grammar, SCFG），它是一种用概率来描述生成规则的形式文法。随机上下文无关文法（SCFG）是一种用来描述语言中句子结构的方法。和一般的文法规则不同的是，SCFG为每一条规则都赋予了一个概率，这个概率表明了某个特定的结构出现的可能性有多大。

随机上下文无关文法（SCFG）：这种文法是在普通的上下文无关文法（Context-Free Grammar, CFG）的基础上，给每条产生规则增加了一个概率值。上下文无关文法是乔姆斯基层级（Chomsky hierarchy）中的第二级文法，可以生成自然语言中的句子结构。

9.3.2.1 术语和概念

        非终结符（Ni）：就是指那些可以被替换为其他东西的符号，比如上面提到的NP（名词短语）。

        终结符和非终结符序列（ζj）：就是那些可以替换非终结符的东西，可以是单词，也可以是其他非终结符。

概率：对于每一条可以替换非终结符的规则，我们都有一个概率来表明这种替换发生的可能性。

句子的概率：一个句子由某个文法生成的概率，是通过计算所有可能得到这个句子的方法的概率的总和来得到的。一个句子属于语法 G 的概率可以通过累加所有可能生成这个句子的句法树`t`的概率`P(w1m,t)`来计算。其中`w1m`代表单词序列。

Njkl分支：想象一下我们把一个句子拆分开来，Njkl 就代表了这个句子中从第k个词到第l个词的一部分。 $Njkl$ 代表非终结符`Nj`下的一个分支，这个分支的叶子节点是从第`k`个单词到第`l`个单词的序列。

不变性条件：这是一些规则，它们保证了无论句子的哪个部分，无论我们考虑哪些单词，或者无论我们处在语法树的哪个位置，某些概率是不会改变的。这就像是说无论你在哪里，规则的使用概率应该是固定的.提出了三个不变性条件，这些条件规定了文法规则的应用概率在特定情况下保持不变：
不变性条件1-空间不变性：对于所有的 k ，非终结符 Njk(k+c) 成序列`ζ`的概率保持不变。
不变性条件2-上下文不变性：非终结符 Njkl 生成序列 ζ 的概率不受外部单词的影响，即不考虑 wkl 之外的单词。
不变性条件3-祖先不变性：非终结符`Njkl`生成序列`ζ`的概率不受它的祖先节点的影响。

产生规则的概率：在SCFG中，每个非终结符 $Ni$ 生成一个终结符或非终结符序列 ζj 的规则都有一个概率 P(Ni → ζj | Ni) 。对于每个非终结符`Ni`，它所有产生规则的概率之和必须等于1，即`∑j P(Ni → ζj | Ni) = 1`。

总结来说，SCFG是一种在生成语法结构时考虑了规则概率的文法，它允许我们计算和预测某个句法结构的可能性，并且提出了在特定条件下这些概率应当保持不变的原则。这样的文法在自然语言处理领域，特别是在句法分析和机器翻译中非常有用。

用一个更简单的比喻：假如有一个餐厅的菜单（文法规则），上面有不同的菜（句子结构）。每道菜被点的几率（概率），有的菜可能很受欢迎（高概率），有的不那么受欢迎（低概率）。SCFG就像是一个带概率的菜单，告诉我们每道菜被选中的可能性。而不变性条件就好比是说，无论是哪位服务员来点菜（空间不变性），顾客点菜时忽略了其他顾客正在吃的（上下文不变性），或者无论菜单的哪个部分（祖先不变性），某道菜被点的几率总是不变的。

9.3.2.2 示例

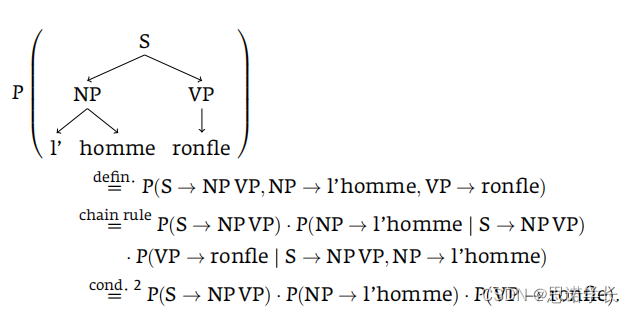
我们的目标是计算整个句子的概率定义，即 $P\left(\begin{array}{c} S\\ VP\\ ronfle\\ NP\\ l'homme \end{array}\right)$ 。使用条件简化计算

9.3.2.2.1 定义

首先，我们定义整个句子的概率为三个产生规则概率的乘积：

$P(S \rightarrow NP\ VP, NP \rightarrow l'homme, VP \rightarrow ronfle)$

9.3.2.2.2 链式规则

使用链式规则（chain rule），我们可以将这个概率展开为：

$P(S \rightarrow NP\ VP) \cdot P(NP \rightarrow l'homme | S \rightarrow NP\ VP) \cdot P(VP \rightarrow ronfle | S \rightarrow NP\ VP, NP \rightarrow l'homme)$

9.3.2.2.3 不变性条件2的应用

根据不变性条件2（上下文不变性），我们知道产生规则的概率仅依赖于规则本身，而与其他规则无关。因此，我们可以简化上述表达式为：

$P(S \rightarrow NP\ VP) \cdot P(NP \rightarrow l'homme) \cdot P(VP \rightarrow ronfle)$

这里，条件2允许我们将复杂的条件概率简化为单独的产生规则概率，因为我们假设每个产生规则的概率独立于其在特定树中的上下文。

9.3.2.2.4 不变性条件1的应用

条件1（空间不变性）允许我们在整个句子或文本中普遍应用这些规则，即不管它们在特定树中的位置如何，规则的概率保持不变。这在本例中意味着无论这些规则在句子中的具体应用位置如何，它们的概率都是固定的。

9.3.2.2.5 结论

通过应用SCFG中的条件2（上下文不变性），我们能够将句子的概率计算简化为三个产生规则概率的乘积。这种方法不仅简化了计算过程，而且提供了对如何组合这些规则以生成特定句子结构的深入理解。条件1（空间不变性）进一步保证了这些规则概率的普遍适用性，从而增强了模型的通用性和灵活性。

9.3.2.3 SCFG的一些关键点

随机上下文无关文法（SCFG）是一种统计模型，用于在自然语言处理中分析句法结构。以下是关于SCFG的一些关键点，用中文详细解释：

9.3.2.3.1 切换到乔姆斯基范式

为了计算方便，我们通常将SCFG转换为乔姆斯基范式（CNF）。我们会把句子的构成规则简化成最基本的形式，这样计算机就更容易理解了，文法只允许以下两种类型的产生规则：

二元规则：形式为 $N_i \rightarrow N_jN_k$ ，这里 $N_i$ 是非终结符，它产生两个非终结符 $N_j$ 和 $N_k$ 的序列。一个部分可以分成两个小部分，比如“句子”可以分成“名词短语”和“动词短语”。
词汇规则：形式为 $N_i \rightarrow w_j$ ，这里 $N_i$ 是非终结符，它直接产生终结符 $w_j$ 。一个部分直接是一个单词，比如“名词短语”可能就是单词“苹果”。

例如，考虑句子“小猫在睡觉”：

在不使用乔姆斯基范式的情况下，我们可能有一个复杂的规则，如：句子 → 主语谓语状语。
在乔姆斯基范式中，我们会将其简化为：句子 → 名词短语动词短语，名词短语 → 形容词名词，动词短语 → 动词状语。

9.3.2.3.2 计算句子的概率

我们使用与隐马尔可夫模型（HMM）类似的技术来计算给定语法G下一个句子的概率。这涉及到计算所有可能的句子结构（句法树）的概率，并将它们相加以得到整个句子的概率。我们会用一种类似于猜测“今天会下雨的概率”这样的方法来计算句子结构的概率。就是说，我们要计算出一个句子按照一定的规则排列起来的可能性有多大。

        假设我们有一个简单的句子“我吃饭”。在我们的语法模型中，可能有以下概率：
        我”作为主语的概率是0.6，
        在“我”之后，“吃”作为动词的概率是0.7，
        吃”后面接“饭”作为宾语的概率是0.8。

那么，“我吃饭”这个句子的结构概率可以大致计算为0.6×0.7×0.8。

9.3.2.3.3 计算最可能的句法树

我们还可以计算一个句子对应的最可能的句法树。这里通常使用Viterbi算法，这是一种动态规划算法，它在计算过程中仅保留最有可能的部分树结构，从而避免了遍历所有可能树结构（其复杂度是指数级的）的需要。Viterbi算法通常具有二次方的时间复杂度，相对于指数级复杂度的穷举搜索，它大大提高了效率。

我们还可以找出一个句子最有可能的结构，这个过程有点像解数学题找出最有可能的答案。我们用一种特别的计算方法，叫做Viterbi算法，这个算法可以帮我们快速找到这个最可能的结构，而不用检查所有的可能性，因为那样太耗时间了。

        考虑句子“猫追老鼠”：
        有两种可能的词性标注，一种是“猫(Noun) 追(Verb) 老鼠(Noun)”，另一种是“猫(Verb) 追(Preposition) 老鼠(Noun)”。
        使用Viterbi算法，我们可以计算哪种词性标注的概率更高。通常情况下，第一种结构因为符合常规语法，其概率会被计算得更高。

9.3.2.3.4 文法归纳方法

文法归纳是一个非常活跃的研究领域，它的目的是从一组预先标注好的句子中识别出文法规则及其概率。这个过程类似于机器学习中的训练过程，目标是找到一套规则，使得生成的句子尽可能地贴近训练语料库中的句子。这些方法可能包括最大似然估计、期望最大化算法等，它们可以用来估计规则的概率，以便更好地匹配训练数据。最后，文法归纳方法就是我们用来找出所有规则和每条规则发生的概率的方法。这有点像我们在学习时通过不断练习和测试来找出最常用的解题方法

        比如我们有一些标注好词性的句子：
        猫(Noun) 喜欢(Verb) 鱼(Noun)”
        狗(Noun) 吃(Verb) 骨头(Noun)”

        通过分析这些句子，我们可以归纳出：
        一个名词通常后面会跟一个动词（概率为0.9），
        一个动词后面通常会跟另一个名词作宾语（概率为0.85）。

这样，通过这些标注好的句子，我们就可以教会计算机识别句子的一般结构和各个词汇之间的关系。

综上所述，SCFG结合了传统的上下文无关文法的形式与概率模型，提供了一种强大的框架来分析和生成自然语言的句法结构。通过将语法规则与概率相结合，SCFG不仅能够描述语言的结构，还能捕捉到语言使用中的不确定性和变化性。### 文法归纳方法

9.3.2.4 SCFG的问题

随机上下文无关文法（SCFG）是一种强大的工具，用于处理自然语言中的句法结构，但它并非没有缺点。下面是SCFG的一些问题，并用中文进行解释：

9.3.2.4.1 不考虑词汇属性

SCFG在分析句子时，不会考虑到单词的词汇属性。比如，它可能会认为“L’homme dort la lune”（男人睡了月亮）这句法文是正确的，因为它没有考虑到动词 dort （睡觉）是不及物的，不应该带宾语。在真实的语言使用中，动词是否及物（即是否需要宾语）是非常重要的，但是SCFG没有能力捕捉这种细节。

        实例：
        正确的法语句子："L'homme dort."（男人在睡觉。）
        错误的法语句子："L'homme dort la lune."（男人睡月亮。）

在第二个句子中，动词“dort”（睡觉）是不及物的，不应该带宾语“la lune”（月亮）。但是SCFG可能不会识别这个问题，因为它不考虑词汇属性，从而可能错误地判定这个句子是语法正确的。

9.3.2.4.2 空间不变性的假设并不现实

SCFG假设规则的概率在句子中的不同位置是相同的，这称为空间不变性。但实际上，这个假设并不符合现实情况。例如，专有名词作为句子主语出现的频率通常远高于作为宾语。这种词汇的偏好用SCFG是很难表示的。

        实例：
        专有名词作为主语："苹果发布了新产品。"（Apple released a new product.）
        专有名词作为宾语："我刚买了一个苹果。"（I just bought an apple.）

在这个例子中，“苹果”（Apple）作为专有名词更常作为句子的主语，表明一个公司名字，而较少作为宾语。然而，在中文里“苹果”作为宾语更多指的是水果。SCFG可能不会区分这种用法上的区别，因为它不考虑词汇在句子中的位置偏好。

综上所述，SCFG在处理某些语言现象时存在局限性。它无法处理涉及词汇特性和位置变化性的复杂语言规则，这在真实语言处理中是非常关键的。因此，尽管SCFG在一定程度上可以模拟句子的结构，但它还需要与其他类型的语言模型或分析技术相结合，以更准确地理解和生成自然语言。

9.4 依赖关系方法

9.4.1 依赖语法（Dependency Grammar）

为了解决SCFG的这些问题，一些研究者提出了基于依赖语法的统计模型和词汇化解析器。

依赖语法关注单词之间的依赖关系，而不是像传统句法分析那样着眼于句子的层次结构。在依赖语法中，句子被视为单词之间的依赖网络，其中每个单词都依赖于句子中的另一个单词（通常是动词或其他关键词），形成一个有向图。

依赖语法关注的是词与词之间的依赖关系，而不是像SCFG那样只关注非终结符的层次结构。

9.4.2 Collins的统计模型和词汇化解析器

Collins的工作：在1996年和1997年，Collins提出了一个基于依赖语法的统计模型和解析器。在他的模型中，对于句子S和它的任意句法树T，模型计算的是条件概率P(T | S)。为了做到这一点，句子S被简化为基础和依赖关系的组合 $\bar{S} = (B, D)$ 。基础B是指句子中的核心词，而依赖D则指出这些核心词与其他词之间的依赖关系。

简单来说，Collins的方法更多地关注单词之间的直接关系，这样不仅可以捕捉词与词之间的配合限制（如及物动词需要宾语），还可以更好地反映语言的实际使用情况（如专有名词通常作主语而不是宾语）。通过这种方法，解析器能够更准确地分析句子的结构。

Collins提出的模型是一个统计模型，它可以计算给定句子的任何依赖树$T$出现的概率$P(T|S)$。在这个模型中，句子$S$被简化为一组基础元素（B）和依赖关系（D）。基础元素通常是句子中的关键词，而依赖关系描述了这些关键词如何相互作用。

例子

假设我们有句子“小猫追着小球玩”：

基础元素（B）:可能包括“小猫”、“追”和“小球”这样的关键词。
依赖关系（D）:描述了这些词之间的关系，例如：“小猫”依赖于“追”（表明“小猫”是主语），“小球”依赖于“追”（表明“小球”是宾语）。

Collins的模型通过分析这些基础元素和依赖关系，计算出该句子结构的概率。这种方法不仅考虑了句子的词汇特性（即词汇化），还考虑了单词之间的依赖关系，从而提供了对句子深层次语义的理解。

总的来说，Collins的工作在自然语言处理领域提供了一种强有力的工具，它通过结合统计模型和依赖语法的优势，能够有效地解析和理解自然语言句子的结构。

9.4.3 示例

以下是由此产生的依赖关系：

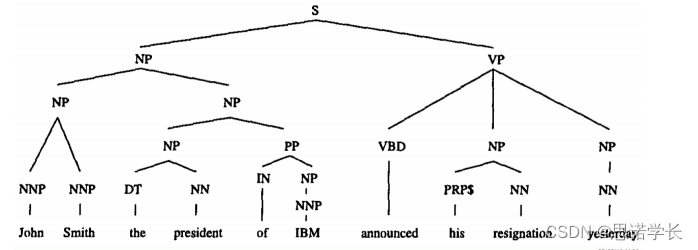
在句法依存关系分析部分，句子是：“John Smith, the president of IBM, announced his resignation yesterday.” 分析的结果以树状结构展示，每个词或短语被分配到了不同的语法类别，比如NP（名词短语），VP（动词短语）等。句子的主体是“John Smith”，被标为NP；“the president of IBM”是一个插入语，提供了关于John Smith的额外信息，也被标为NP；动词“announced”构成了VP；而“his resignation”是宾语，被标为NP。时间状语“yesterday”提供了动作发生时间的信息。

这是B组和D组：

集合B包括短语：“John Smith”，“the president”，“IBM”，“his resignation”，“yesterday”。这些短语可能是根据句子中的关键成分提取出来的。

集合D包含一些可能由原句中的词汇重组而成的短语：“Smith announced”，“Smith president”，“president of”，“of IBM”，“announced resignation”。这些组合展示了原句中的词语如何相互关联。

9.4.4 简化语法树

a.找到头节点-子节点对：首先，对于语法树中的每个中间节点，通过一个决策树算法（可能是Jelinek等人在1994年提出的一种算法）来找出所谓的头节点，也就是最能代表该中间节点核心意义的子节点。

找到它们与其子节点之间的关系。这种关系可以被理解为一个节点在语法树中的位置，以及其直接子节点的位置。

语法树是一种树形结构，其中的每个节点代表了一个语言单位，如单词或短语。在这种方法中，我们对语法树中的每个节点进行处理，找到它们与子节点之间的关系。这个关系指示了一个节点在树中的位置以及它们直接连接的子节点。

b.向上移动头节点-子节点对：接下来，将找到的头节点-子节点对尽可能地向上移动，也就是在树结构中提升它的位置，让它更靠近根节点。

这意味着将子节点连接到它们的最近共同父节点。这样做有助于简化树结构并减少树的深度。这样做可以使树的结构更加简单化，同时减少树的深度。

c.提取依存关系：一旦头节点-子节点对已经移动到树中的适当位置，就可以提取出它们之间的依存关系。

这些依存关系指示了树中各个部分之间的语法关系，例如修饰关系或动词与其宾语之间的关系。

一旦头节点-子节点对已经移动到了适当的位置，我们就可以提取出它们之间的依存关系。依存关系表示了一个词或短语与另一个词或短语之间的语法关系，比如主谓关系或修饰关系。在树结构被压平后，从中提取依存关系。

d.生成依存关系：每个具有n个子节点的成分（如短语结构）会产生n-1个依存关系。这意味着，根据简化后的结构，每个成分会产生对应数量的依存关系。每个具有n个子节点的成分会产生n-1个依存关系。这意味着，对于每个成分，我们需要生成相应数量的依存关系，以确保树结构的完整性和准确性。

e.学习与分析：在简化后的结构上，解析器会对依存关系的三元组进行学习，以更好地理解和处理语言。简单来说，这是一种让复杂句子结构变得更简单、更容易分析的技术。

这意味着解析器会分析这些关系，学习它们在不同语言结构中的出现频率和模式，并根据这些模式来理解和生成句子的结构。

在得到简化的树结构和相关的依存关系之后，解析器会对这些信息进行学习和分析。这意味着解析器会尝试理解这些依存关系在不同句子中的出现模式，并根据这些模式来预测句子的结构或生成新的句子。

压平（flattening）树结构意味着将原本多层的树转变成更为扁平的形式，这样做可以简化句子的结构，并更容易地看出词语之间的直接依赖关系。每当有一个构成成分（constituent）含有n个子节点时，就会产生n-1个依存关系，因为每个子节点（除了头孩子）都会与它的父节点产生依存关系。

通过这种方式，该方法利用依存关系来分析句子结构，并在简化后的结构上进行学习，以实现更高效和准确的语法分析。

10 第二分枝——浅层分析（或称块分析）

浅层解析（Shallow Parsing）或称为分块（Chunking），是句法分析的简化版。不同于找到一个完整的句法树，浅层解析仅仅满足于识别出句子的表层结构。这种方法非常适用于信息提取或文档分类等任务。

9.5.1 浅层解析的定义

分块（Chunking）：是指将一个句子分解成若干个较大的片段（称为“块”或“chunk”），每个块通常包括一个核心词（如名词、动词等）及其修饰词（如形容词、副词等）。

9.5.2 块（Chunk）的概念

根据Abney在1994年的定义，一个“块”可以是任何非语法性的词w以及它周围的语法性词汇，除非w位于另一个词w′和一个依赖于w′的语法性词之间。
例如，在“a big proud man”（一个骄傲的大个子男人）中，虽然“big”、"proud"和“man”都是名词，整个短语却被视为一个单一的块，因为“a”依赖于“man”。

9.5.2 浅层解析的应用

浅层解析特别适用于那些不需要深入理解句子完整结构的场合。例如，在信息提取中，我们可能只关心句子中的特定信息，比如提取组织名、人名或地点名；在文档分类中，我们可能根据关键短语的出现频率来判断文档的主题或类别。

9.5.3 心理学依据

Abney的定义还基于心理学研究，这些研究表明人们在理解句子时，并不总是构建完整的句法结构，而是倾向于识别出句子中的关键信息块。这说明在很多实际应用场景中，浅层解析可能就足够了，因为它能快速提供关键信息，同时减少计算复杂度。

总的来说，浅层解析或分块提供了一种高效的方式来处理自然语言，特别是在需要快速提取关键信息而不需深入分析句子结构的应用中。这种方法虽然简化了句法分析的过程，但在很多场景下已经足够有效。

9.5.4 分块（chunking）

在介绍浅层解析中的一个特定概念，即分块（chunking）。这是自然语言处理中的一种技术，用来识别句子中的短语或“块”，而这些块代表着更大的语法单元。来自Sha和Pereira在2003年的研究中对分块的定义如下：

        分块（Chunks）：它们被定义为句子中各个组的非递归核心。非递归核心是指这些短语不包含任何嵌套的小短语或子块，简而言之，分块是简单、不包含其他块的短语。

        句子分解：由于块是非递归的，因此当我们将句子拆解时，它的结构总是平面的，没有更深层次的嵌套结构。例如，给出的例子句子通过分块可以清楚地看到，句子被分解为了名词短语（N）和动词短语（V）等基本组成部分。

        例子：[Indexing]N [for the most part]N [has involved simply buying]V [and then holding]V [stocks]N [in the correct mix]N [to mirror]V [a stock market barometer]N.在这个例子中，每个方括号内的内容代表一个块，每个块后面的字母代表该块的类型（名词N或动词V）。

Illinois Chunker：这是一个可以识别10种不同类型块的工具，例如形容词短语（ADJP），副词短语（ADVP），连接短语（CONJP），感叹词（INTJ），列表标记（LST），名词短语（NP），介词短语（PP），小品词（PRT），从句（SBAR），动词短语（VP）等。例如，“Jack and Jill” 是一个名词短语（NP），而“went” 是一个动词短语（VP），“up” 是一个副词短语（ADVP），如此类推。

分块是自然语言处理中的基础步骤，它帮助处理器快速识别和分类句子中的不同成分，而无需深入到更复杂的句子结构。通过识别这些基本的块，可以进一步分析句子的语法和意义。

9.5.5 如何标记分块

这段文字进一步解释了浅层解析中的一个特定方面，即如何标记分块。我们通常将分块限制在名词短语或"nominal chunks"内。在这个上下文中，每个单词都会被分配一个特定的标签，以指示它在分块中的位置：

        1. `O`（Outside）标签用于表示一个单词不属于任何分块。
        2. `B`（Beginning）标签用于表示一个单词是分块的第一个单词。
        3. `C`（Continuing）标签用于表示一个单词属于某个分块，但不是第一个单词。

为了实现这种标记，Ramshaw和Marcus在1995年的研究中使用了变换规则。这些规则考虑了给定单词左右各自最多三个单词或词性标签（POS tags）。词性标签是单词在语言学中的分类标记，比如名词、动词、形容词等。

从1992年到2001年间，研究者们尝试了多种技术来处理这个问题，包括：

        隐马尔可夫模型**（HMM）
        最大熵马尔可夫模型**（MEMM）
        Winnow** 算法
        AdaBoost**，这是一个用于提升弱学习器性能的算法
        支持向量机**（SVM）
        泛化感知机**（generalized perceptron）

例如，Sha和Pereira在2003年的研究中使用了条件随机场（CRFs）来解决这个问题。对于某个单词wi，他们使用了这个单词前后各自两个单词（wi-2, ..., wi+2）和相应的词性标签（ti-2, ..., ti+2），以及当前单词的分块标签（yi）和下一个单词的分块标签（yi+1）作为特征。

简而言之，这段话描述的是如何使用机器学习和序列标注方法来标记句子中的分块，这对于自然语言处理和文本分析是非常重要的步骤。