【ML】类神经网络训练不起来怎么办 5
-
- 1. Saddle Point V.S. Local Minima(局部最小值 与 鞍点)
- 2. Tips for training: Batch and Momentum(批次与 动量)
-
- 2.1 Tips for training: Batch and Momentum
- 2.2 参考文献:
- 2.3 Gradient Descent
- 2.4 Concluding Remarks(前面三讲)
- 3. Tips for training: Adaptive Learning Rate ,Error surface is rugged ...
-
- 3.1 凸优化 使用 同意的learning rate 可能出现的问题
- 3.1.2 Warm Up
- 3.2 Different parameters needs different learning rate(客制化 learning rate)
- 3.3 RMSProp 是一种自适应学习率优化算法,它可以根据梯度的均方根来调整每个参数的学习率。
- 3.4 Adam: RMSProp + Momentum
- 3.5 Summary of Optimization
- 4. Loss 影响
1. Saddle Point V.S. Local Minima(局部最小值 与 鞍点)
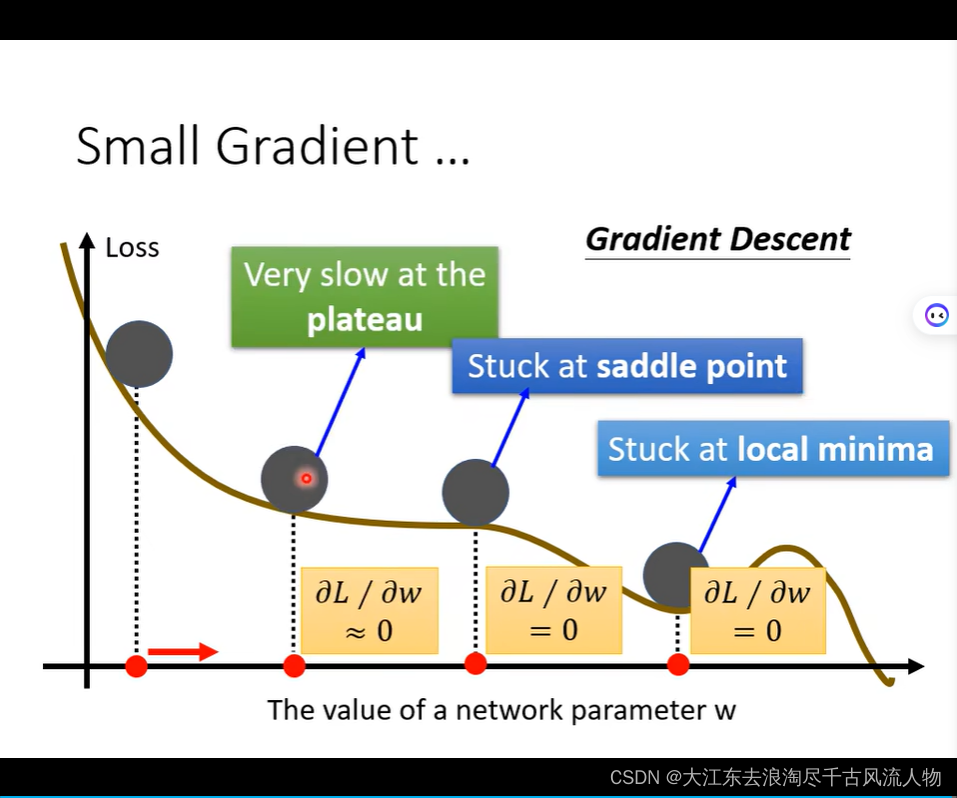
Optimzation Fails,Why?
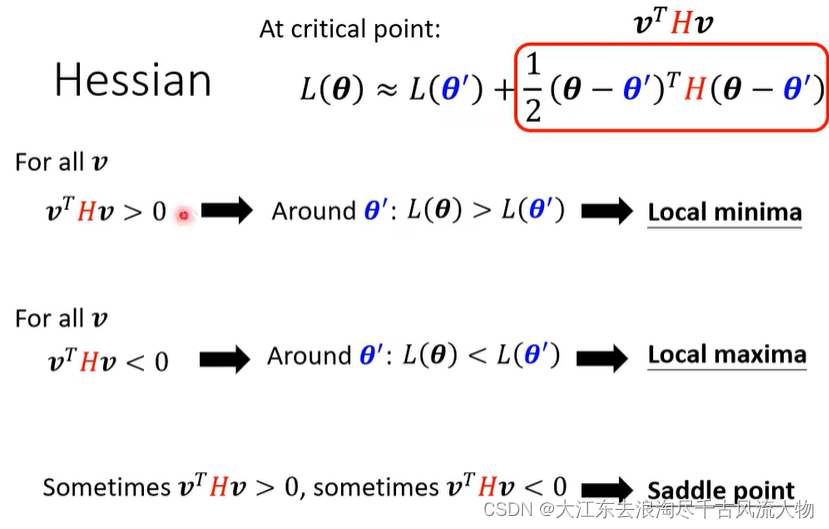
gradient is close to zero , 2 situation : local minima or saddle point ,we call this critical point.
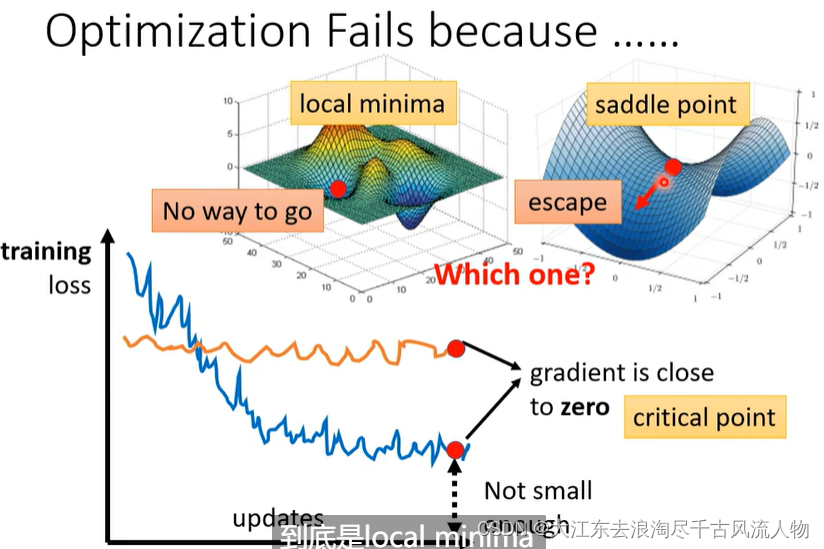
如何判断 是 local minima or saddle point中的哪一种情况呢?
我们采用Taylor的展开来求解:

求零点附近的Hessian矩阵,根据Hessian矩阵判断是哪一种情况

实现步骤如下:
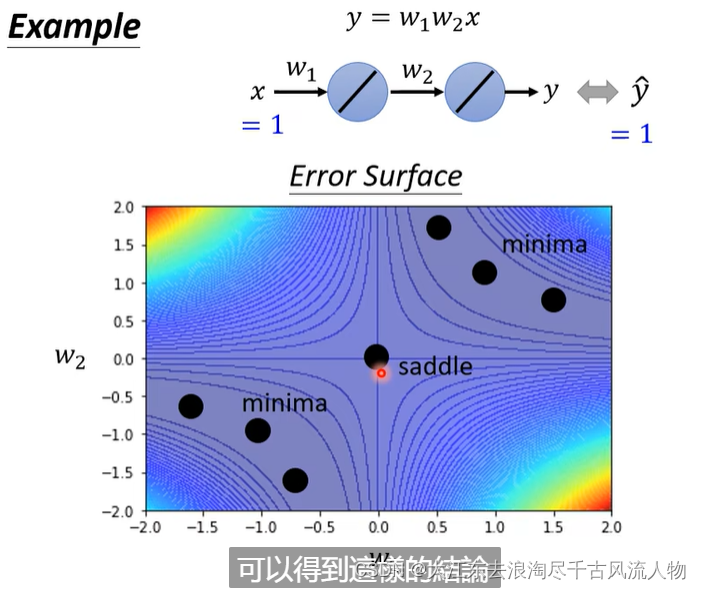
举例说明:
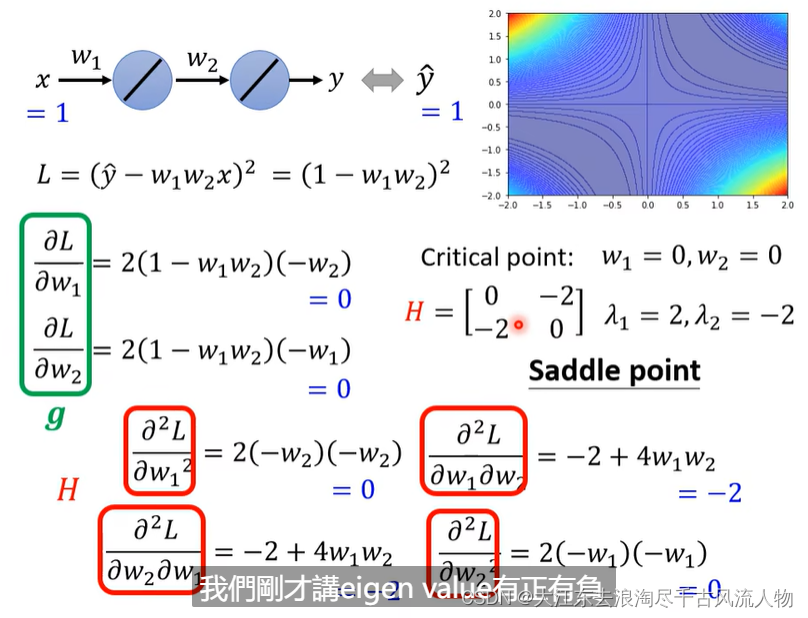

saddle point 在训练过程中出现该怎么处理 hessian matrix 处理Saddle Point 逃离
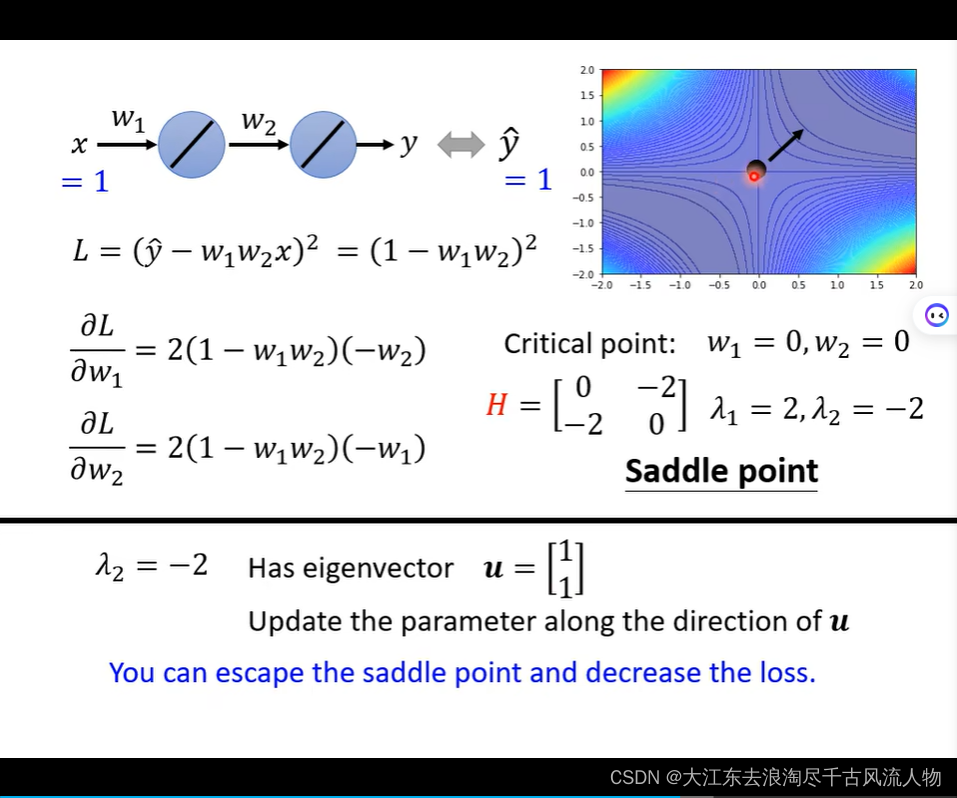
站在更高的维度去处理解决问题:

2. Tips for training: Batch and Momentum(批次与 动量)
2.1 Tips for training: Batch and Momentum
同一个数据集合 :做batch 然后shuffle这些batch

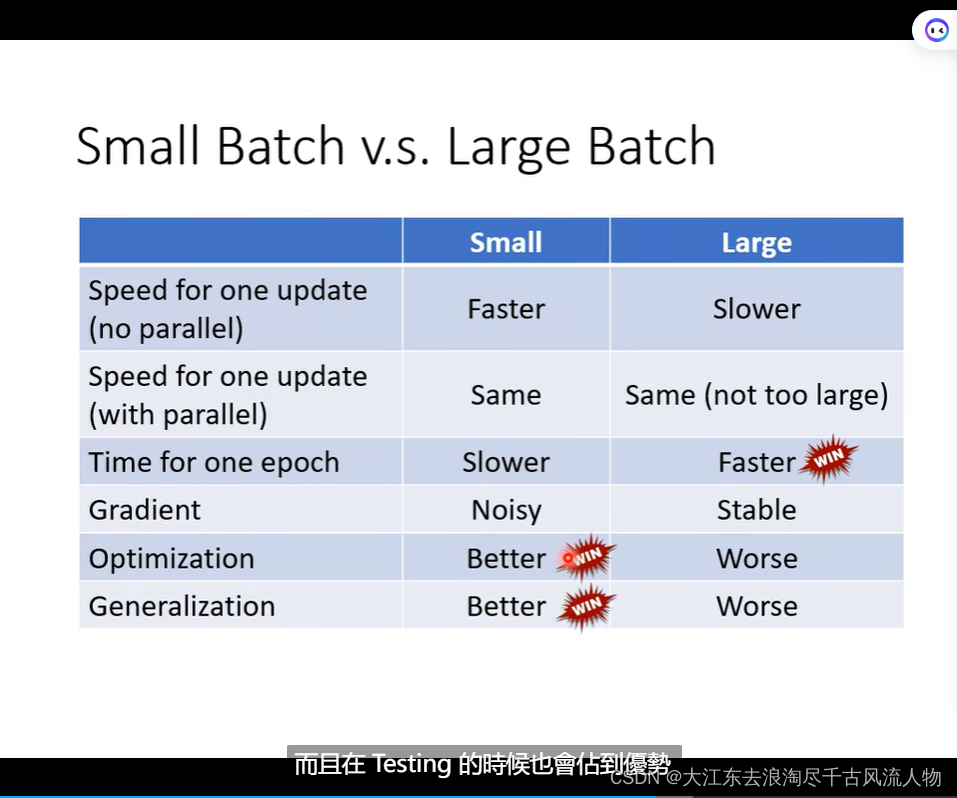
Small Batch v.s. Large Batch 优缺点对比

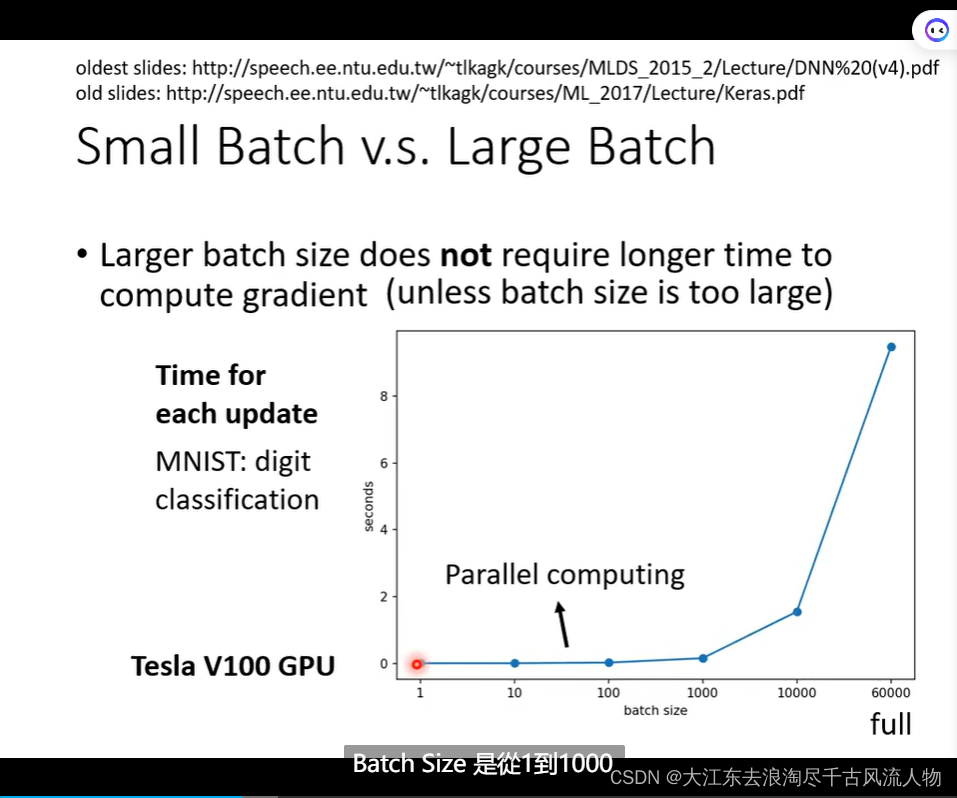
不考虑 并且运算的情况下 Epoch 大的跑的快
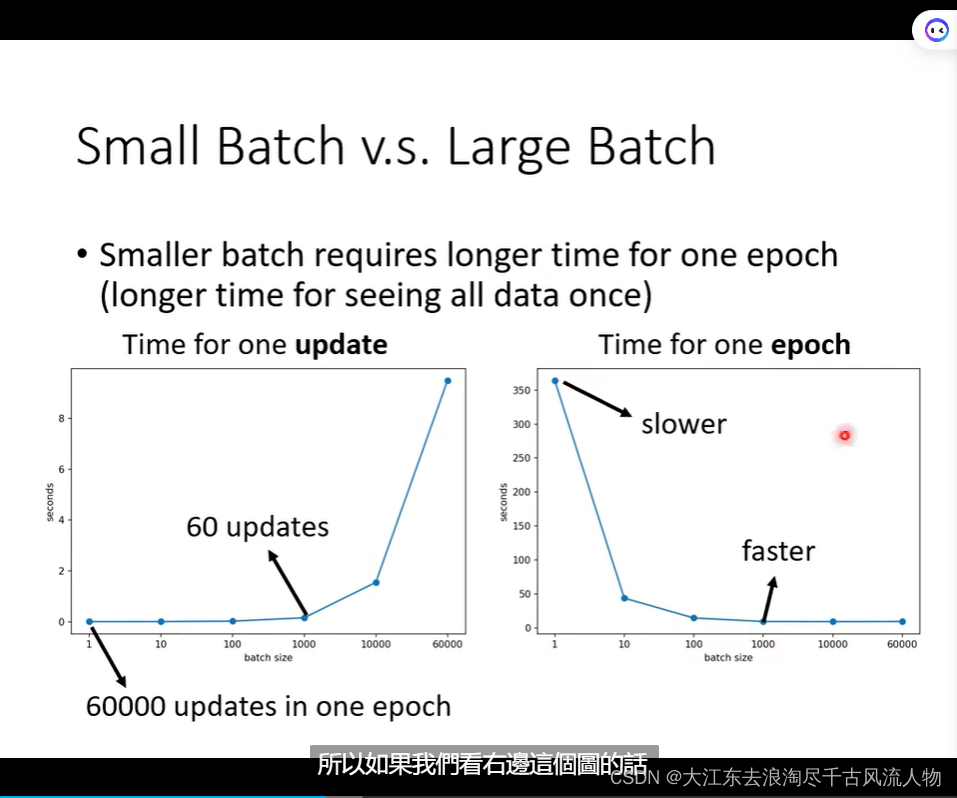

大的batch 结果好的原因是什么?

上面这个问题下面给出答案:
Small Batch v.s. Large Batch
Smaller batch size has better performance
“Noisy” update is better for training.
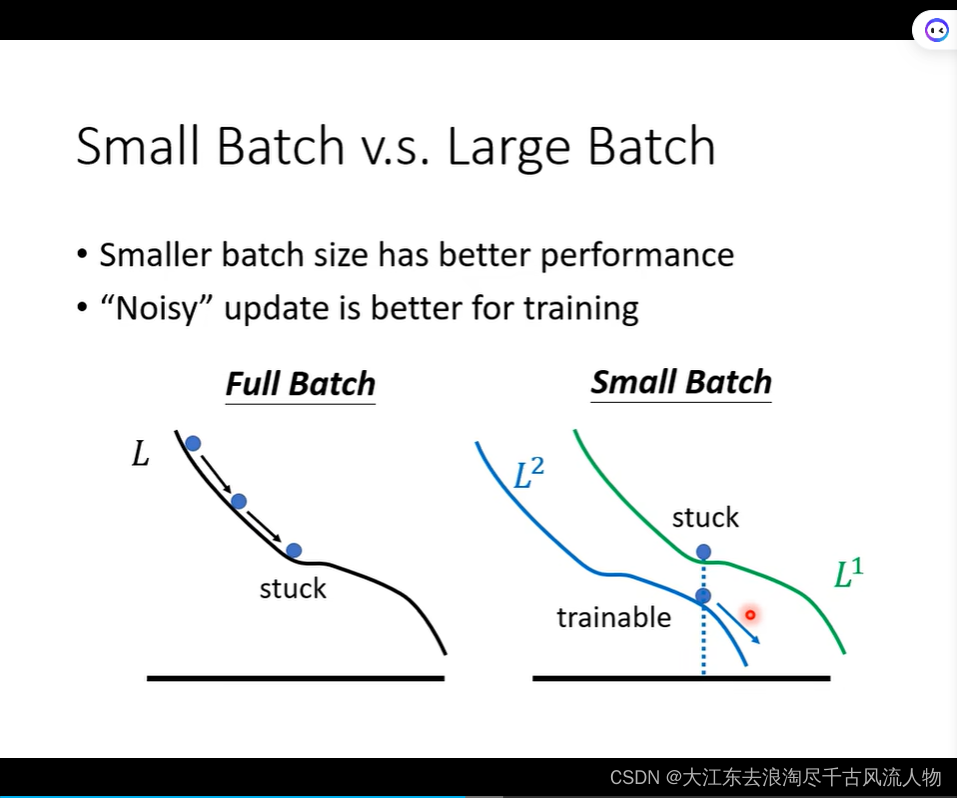
Small batch is better on testing data!

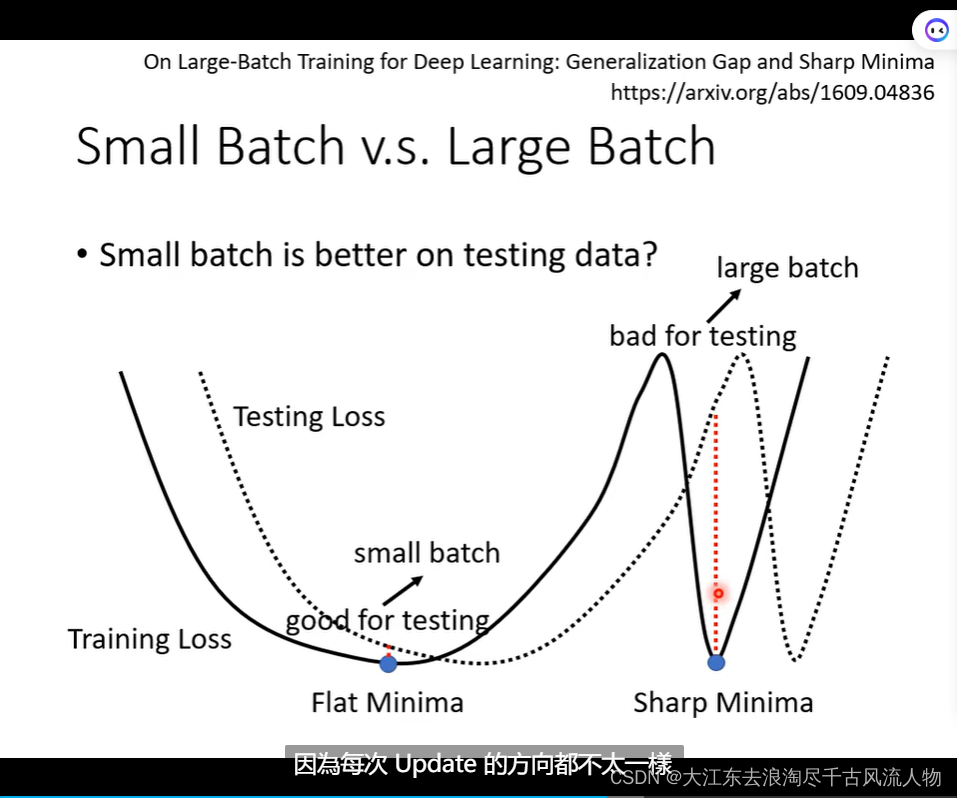
Small Batch v.s. Large Batch: 详细的优势掠食 对比,在并行情况下,速度持平,除非,大的batch特别大
但是大的batch在update的时候比较快(优势);小的batch 的优化洁后果和泛化性能更好;
Batch size is a hyperparameter you have to decide.
2.2 参考文献:
Have both fish and bear’s paws?
- Large Batch Optimization for Deep Learning: Training BERT in 76 minutes (https://arxiv.org/abs/1904.00962)
- Extremely Large Minibatch SGD: Training ResNet-50 on ImageNet in 15 Minutes (https://arxiv.org/abs/1711.04325)
- Stochastic Weight Averaging in Parallel: Large-Batch Training That Generalizes Well (https://arxiv.org/abs/2001.02312)
- Large Batch Training of Convolutional Networks
(https://arxiv.org/abs/1708.03888) - Accurate, large minibatch sgd: Training imagenet in 1 hour
(https://arxiv.org/abs/1706.02677)
2.3 Gradient Descent
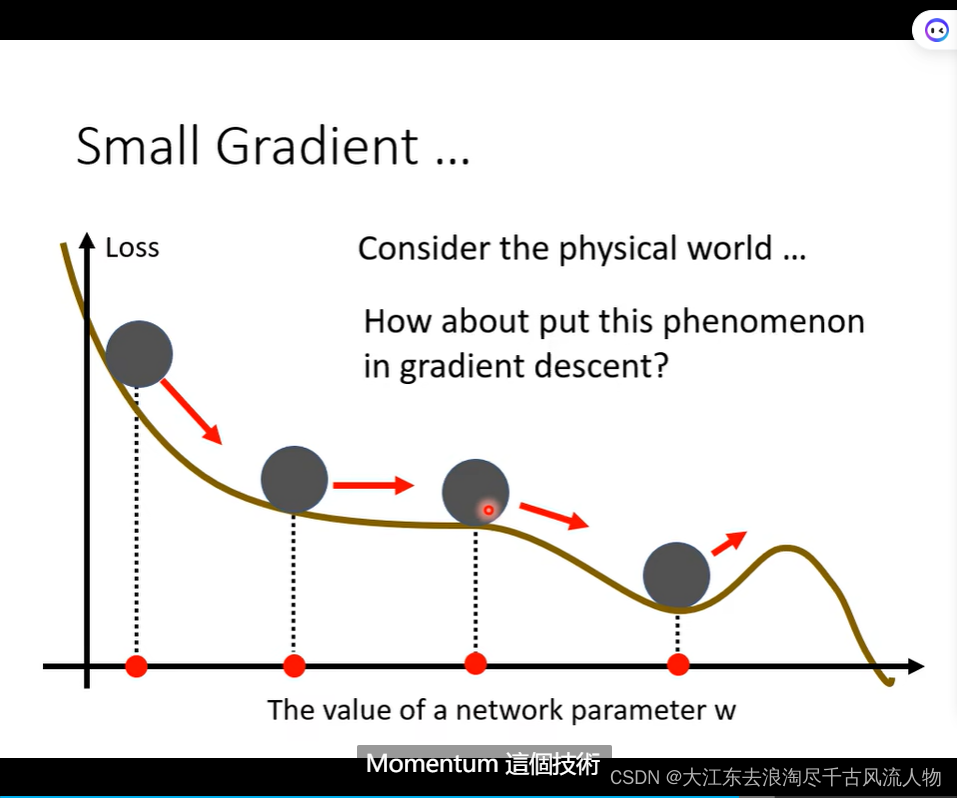
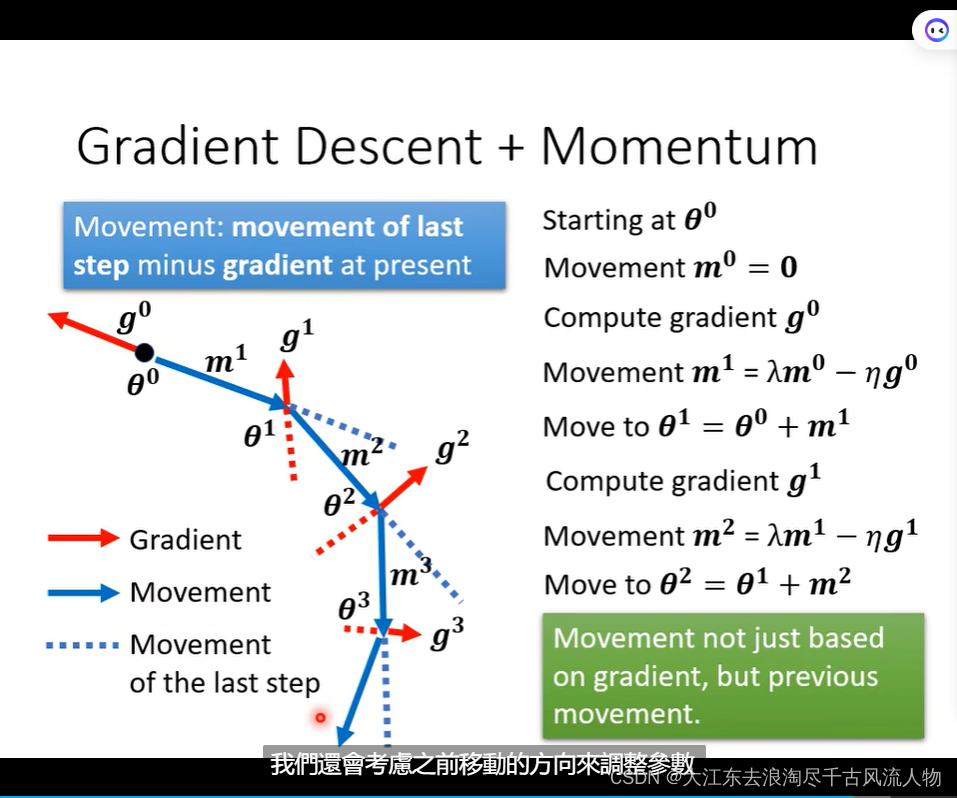
考虑过去 Gradient 过去的总和:

Gradient Descent + Momentum 一大好处就是Gradient Descent退化时候,依然可以继续优化步骤,而不是导致优化停止。