引言

这是李宏毅老师深度强化学习视频的学习笔记，主要介绍策略梯度的概念，在上篇文章的末尾从交叉熵开始引入策略梯度。

如何控制你的智能体

上篇文章末尾我们提到了两个问题：

• 如何定义这些分数$A$，即定义奖励机制；
• 如何采样这些状态和动作对；

版本0

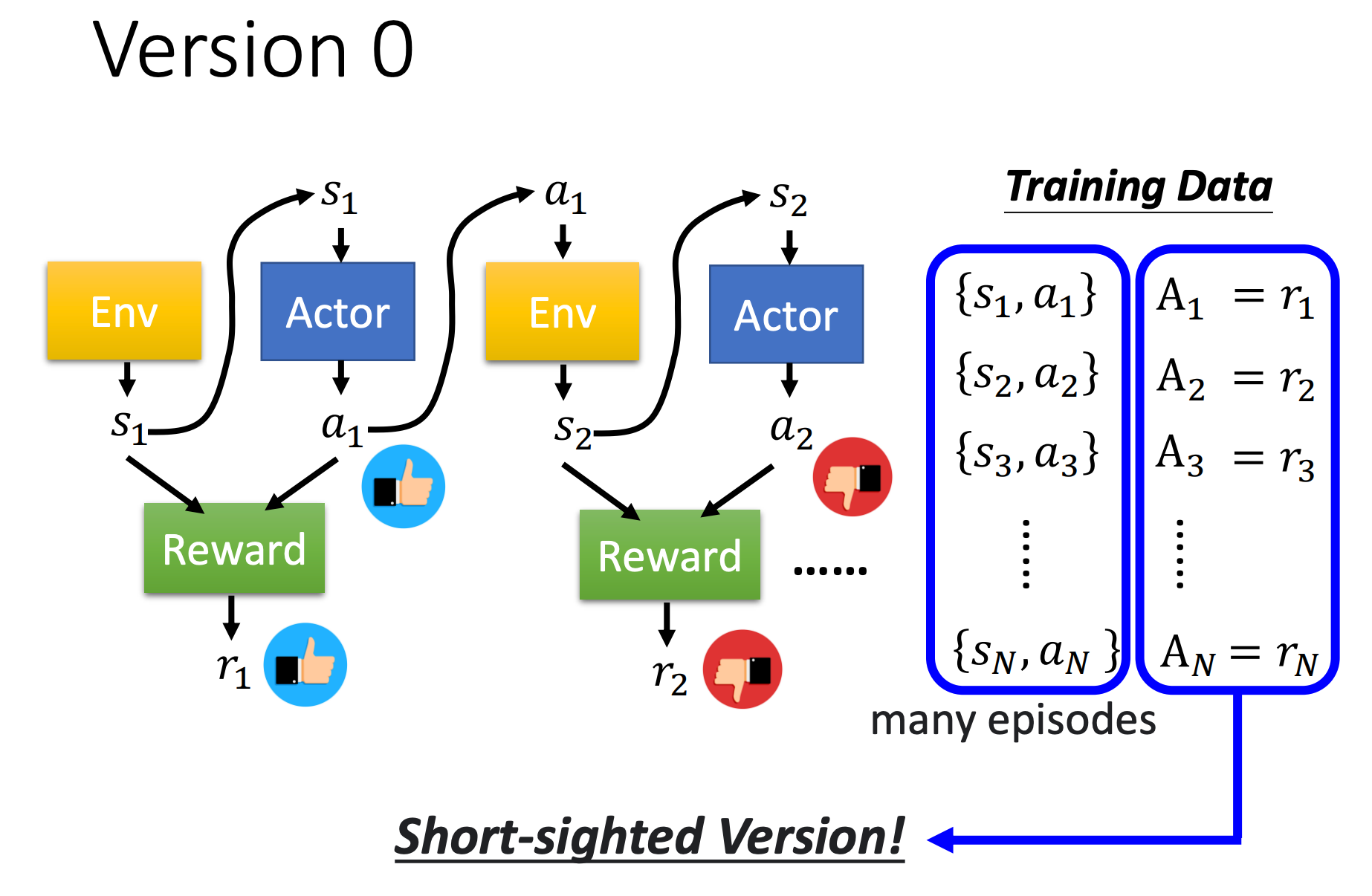
我们先来看一个最简单，但不正确的版本。

首先要收集状态-动作对，其实很简单，需要先有一个智能体，这个智能体很傻也没关系，让它去和环境互动，记录互动过程中看到的状态和产生的动作，就可以收集这些状态-动作对。通常我们做多个episode，就可以收集到很多数据，如上图蓝框所示。

这里说这个智能体很傻也没关系，指的是刚开始我们可以随机初始化这个智能体(神经网络)。

收集到这些数据后，我们就可以评价每个动作的好坏，评价就是看智能体在某个状态下执行的动作所得到的分数有多少，这个分数(就是奖励)可正可负可零，正的越多表示这个动作越好，负的越多表示这个动作越不好。

这样我们可以把分数$A$和奖励$R$关联起来：$A_i=r_i$。
如果智能体在看到$s_1$执行动作$a_1$后得到的奖励$r_1$是正的，就代表这是一个好的动作，以后尽可能执行这个动作。
如果智能体在看到$s_2$后执行动作$a_2$得到的奖励$r_2$是负的，就代表是一个坏的动作，以后不要执行这个动作。

⚠️ 这里说尽可能是为了增加随机性(探索性)，可能执行$a_1$虽然好，但不是最好的；还有可能先执行一个负奖励的动作，但后面可以得到正奖励超大的很多的动作(下一个版本会看到)。因此通常在训练时会引入一个随机性来探索更多的可能性。

这并不是一个很好的版本，因为通过这种方法训练出来的智能体非常短视，没有长期规划，每次只会执行当前状态下奖励最高的动作。但是当前采取的每个动作会影响接下来互动的发展。

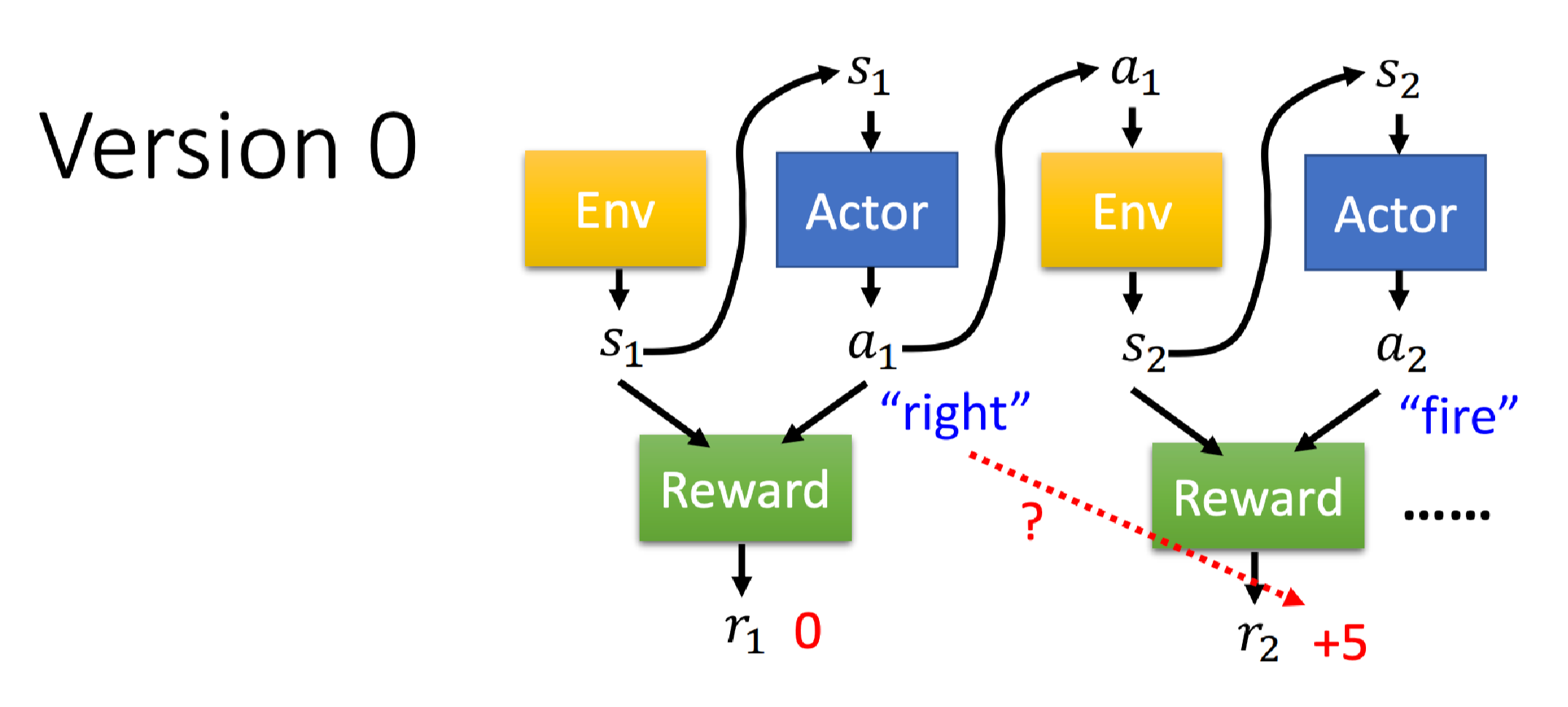
比如在看到$s_1$采取$a_1$会得到奖励$r_1$，但是会影响环境产生$s_2$，从而影响了奖励$r_2$。

举个例子，闯红灯是不好的(奖励-1)，但如果车上有需急救病人，那么闯红灯可以更快地到达医院(奖励+100)，那么这种情况下应该更灵活一点。

实际上智能体在和环境互动时还可能存在奖励延(Reward delay)问题，例如上面说的最大的奖励+100，智能体要学习牺牲短期奖励(瞬时奖励)来获取更多的长期奖励。

如果我们使用版本0来玩外星人入侵游戏，因为只有开火凯能获得正奖励，那么版本0会训练一个只会开火的无情机器，但不会躲弹的话很快就可以开下一把。

版本1

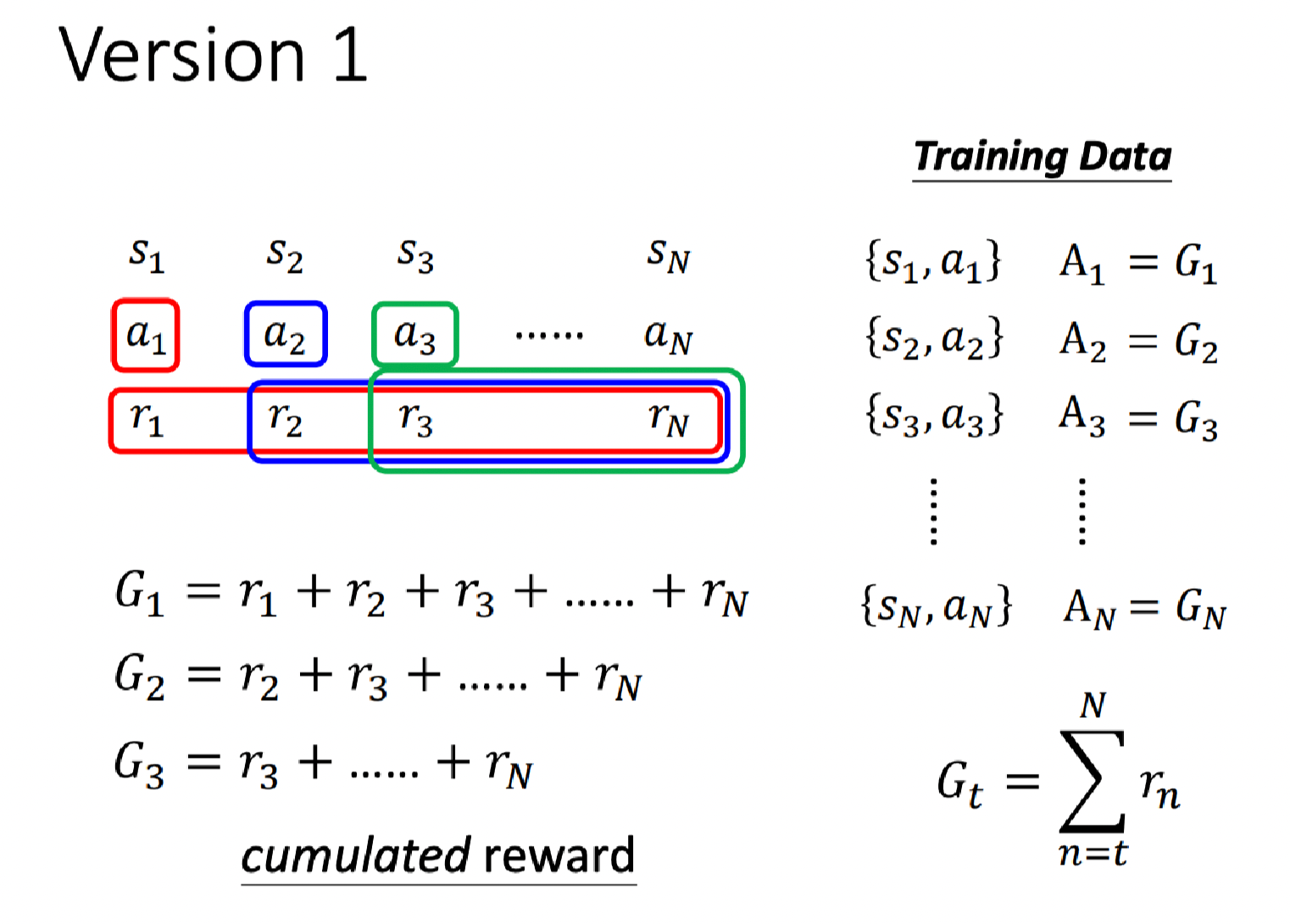
所以我们评价动作$a_1$有多好，不应该只看$r_1$，而是要看$r_1$和后续所有的奖励总和$G_1=r_1+r_2+r_3+\cdots +r_N$。然后我们令$A_1=G_1$。

以此类推，评价动作$a_2$有多好，要通过$G_2=r_2+r_3+\cdots +r_N$来看。

这里的$G$称为累积奖励(cumulated reward)：
$$G_t=\sum _{n=t}^N{r}_n$$

这个版本就可以解决智能体短视的问题，假设$a_1$是向右，没有立即的奖励，但是向右恰好躲掉了外星人的子弹，那么就可以存活的更久，也就会有更多的机会开火，最后得到的累积奖励更高。

但是版本1也有点问题，就是把后续所有的奖励和当前的奖励同等看待(默认前面的权重全为1)，虽然我们做了$a_1$，最后得到了$r_N$，是有一定的影响，但不应该这么高吧，更多的应该是和执行动作$a_N$有关。

版本2

所以我们引入一个折扣因子$\gamma <1$来表示后续影响持续衰退这件事情。
以执行动作$a_1$为例，瞬时奖励$r_1$前的系数还是设为1，因此此时受该动作影响最大。但后续的奖励我们累乘这个因子：
$$G_1^{\prime }=r_1+\gamma r_2+{\gamma }^2{r}_3+\cdots$$
即使距离动作$a_1$越远，$\gamma$项乘的就越多。
得到了累积奖励的衰退版本：
$$G_t^{\prime }=\sum _{n=t}^N{\gamma }^{n-t}{r}_n$$

这个版本已经很好了，但是还有一个小问题。

版本3

奖励的好与坏其实应该是相对的，假设是一个非常解压的游戏，没有负奖励，类似场景中有非常多的金币，没有陷阱和阻碍，只要碰到金币就能拿到超过10的奖励，没有碰到也有10的奖励。那么相对来说，奖励10就是不好的。

所以我们可以引入一个偏置(baseline，这里通常翻译成偏置而不是基准)b，让奖励有正有负。
如上图所示，我们让每个$G^{\prime }-b$。

听起来不错，但又引入了一个新的问题，我们要如何设定这个偏置大小呢？

下面正式进入策略梯度，它也包含了这个问题的解决。

策略梯度

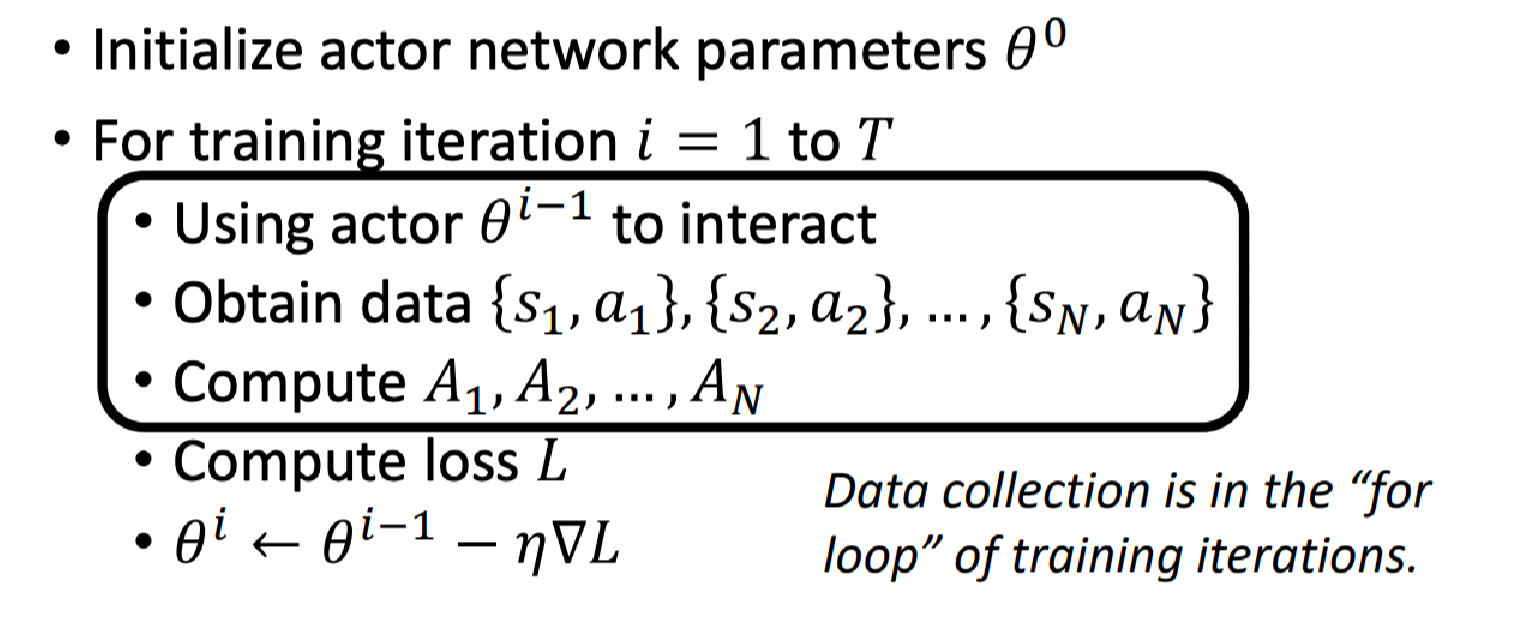
我们先来看下策略梯度(Policy Gradient)的算法。

• 首先随机初始化Actor网络(表示执行动作的智能体网络，下文都用Actor表示)，假设此时初始化参数为${\theta }^0$；
• 进入训练迭代，假设迭代$T$次，每次迭代记为$i$：
  • 使用上次迭代的Actor(${\theta }^{i-1}$)去与环境互动；
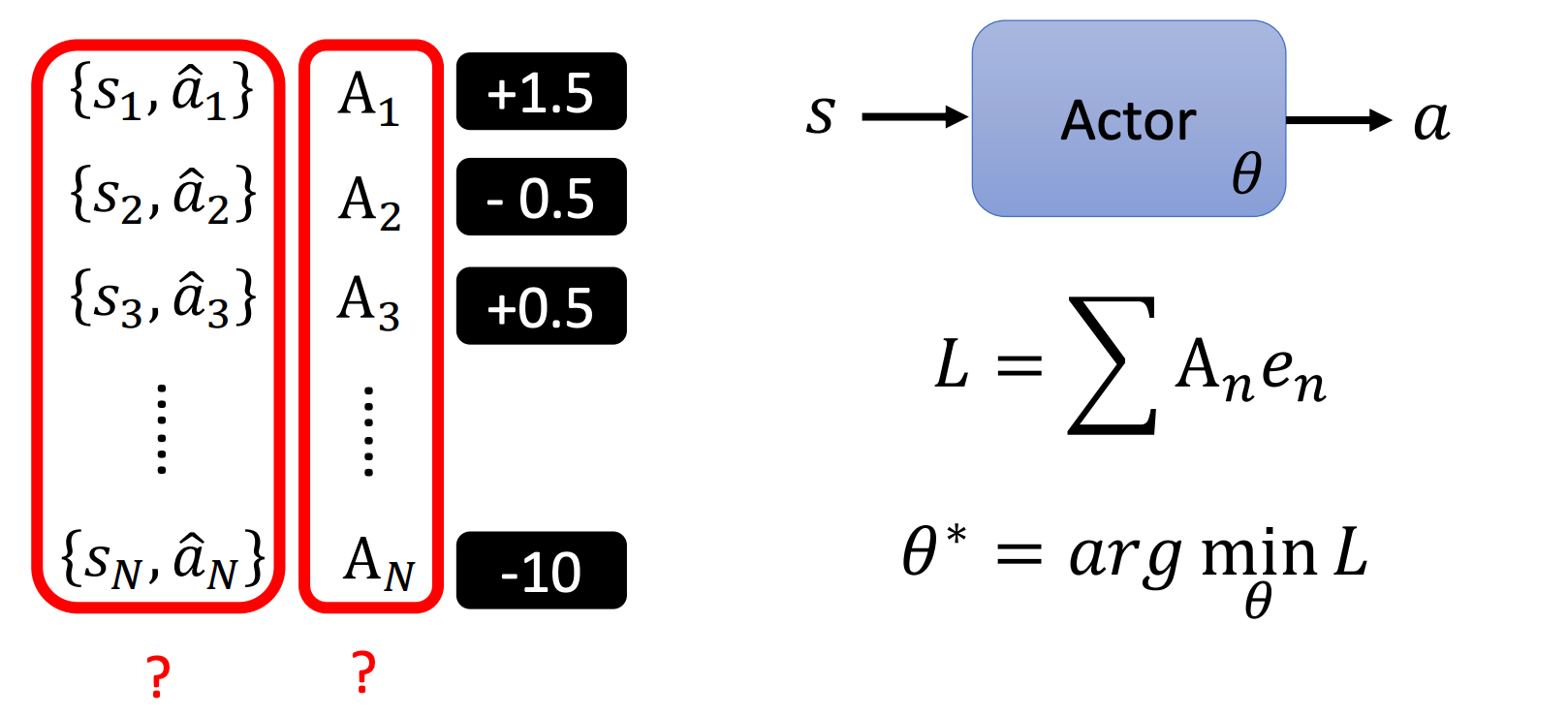
  • 得到状态-动作对数据： { s 1 , a 1 } , { s 2 , a 2 } , ⋯   , { s N , a N } \{s_1,a_1\},\{s_2,a_2\},\cdots,\{s_N,a_N\} {s1​,a1​},{s2​,a2​},⋯,{sN​,aN​}；
  • 评价这些动作的好坏：计算$A_1,A_2,\cdots ,A_N$；
  • 定义损失$L$(该步以及下一步和梯度下降类似)；
  • 更新网络参数：${\theta }^i\leftarrow {\theta }^{i-1}-\eta \nabla L$；

算法重点的区别在于$A$的定义。
这里要注意的是数据的收集是在训练循环内，通过上次迭代得到的网络来做的。

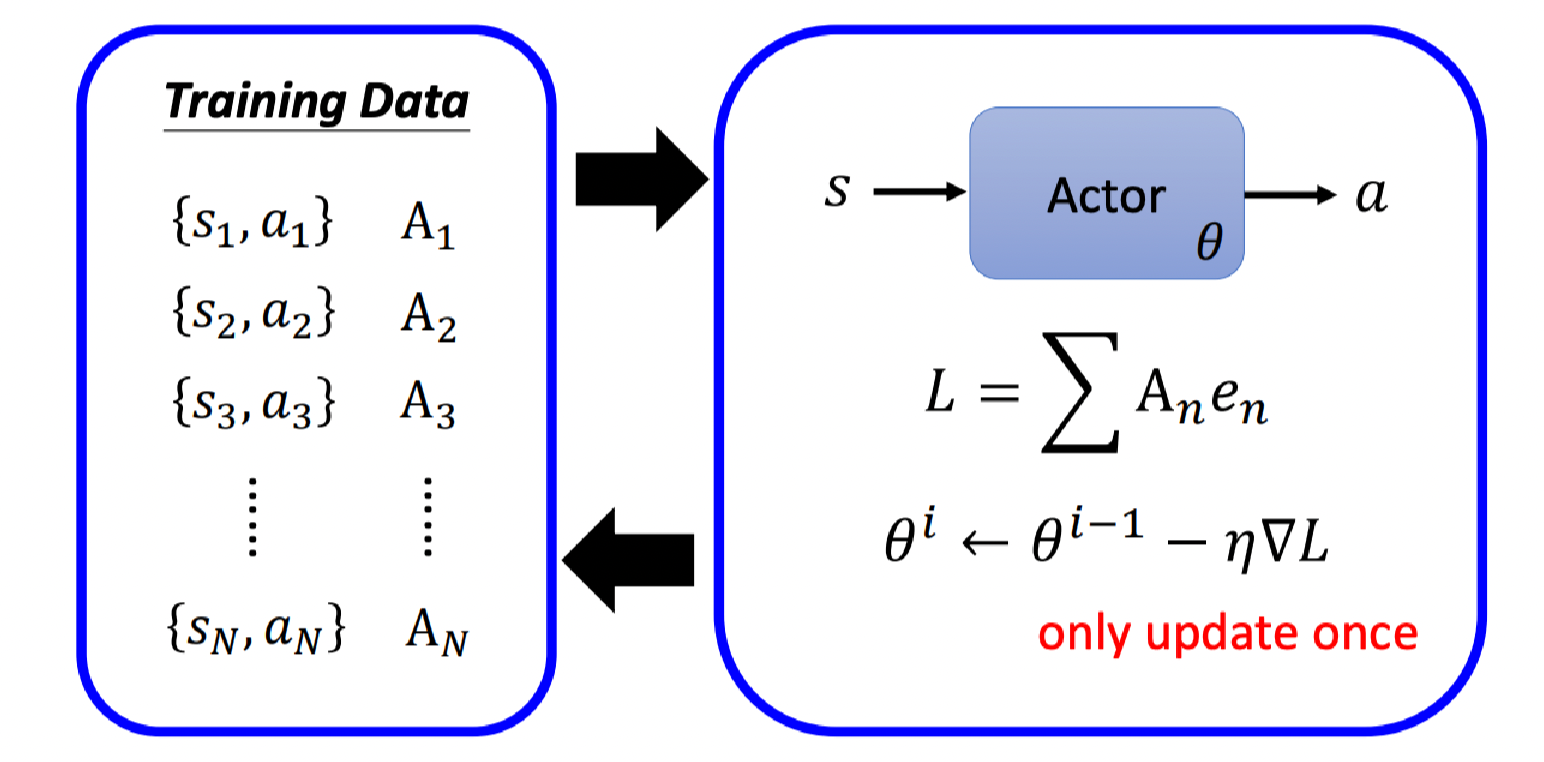
我们用图像化来表示，左边是收集到的数据，观测Actor在每个状态执行的动作，然后给予一个评价$A$；然后拿这个评价定义一个损失来训练Actor；接着计算这个损失的梯度来更新一次Actor的参数；然后用更新后的Actor来重新收集数据；…

所以这样训练起来往往会耗时较久，因为我们在循环内还要执行收集数据这件事。

为什么我们每次要重新收集数据，而不是一直使用一份数据呢？

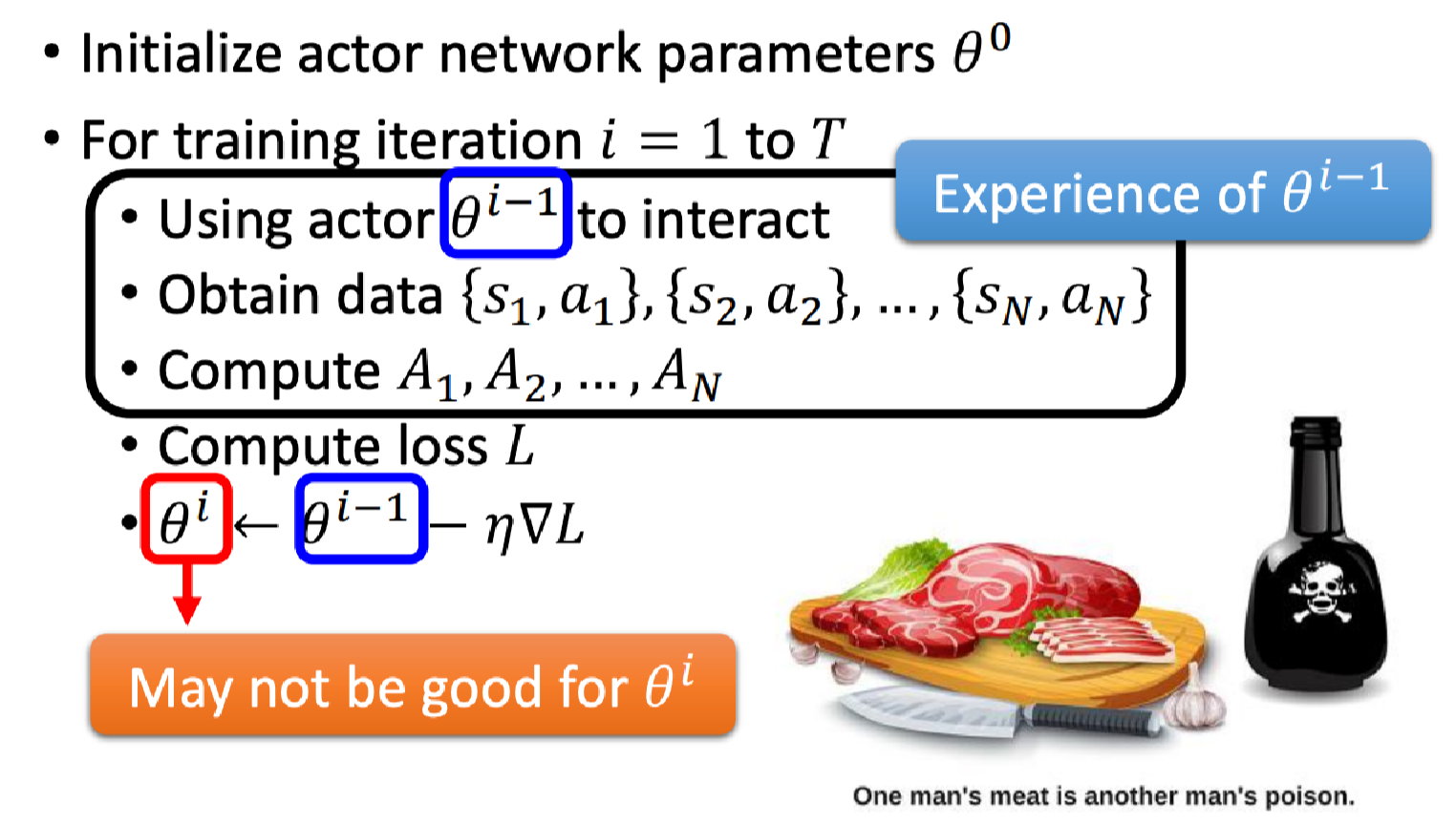
这里用一个简单的比喻，一个人的食物可能是另外一个人的毒药。
具体来说，${\theta }^{i-1}$所获得的经验(收集到的数据)对${\theta }^i$来说不一定是好的。

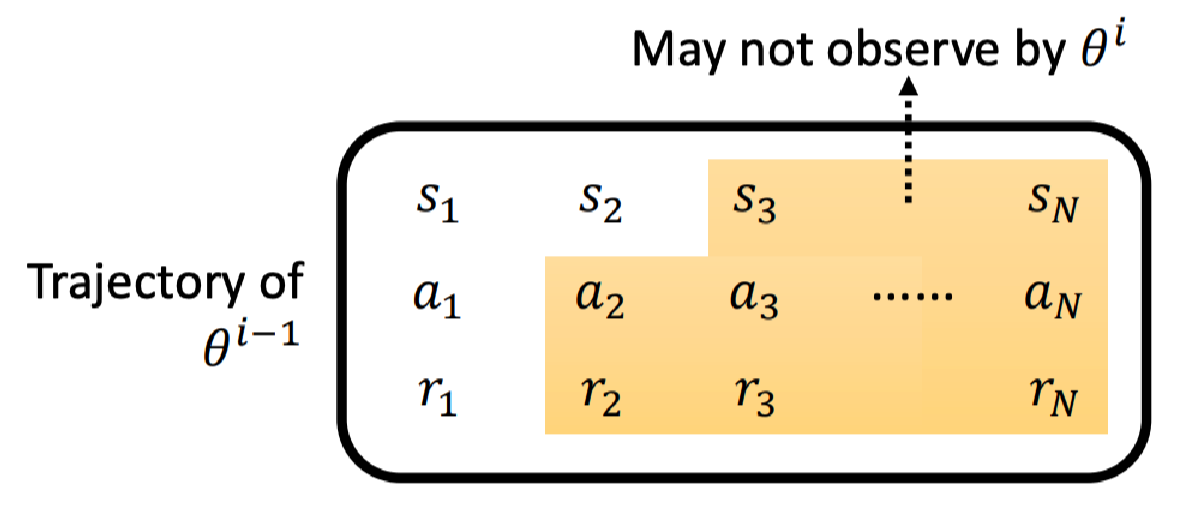
或者说，${\theta }^{i-1}$的轨迹不一定会被${\theta }^i$观测到。
假设它们都可以在$s_1$采取$a_1$；但可能在$s_2$后采取的行为就不一样了。

On-policy v.s. Off-policy

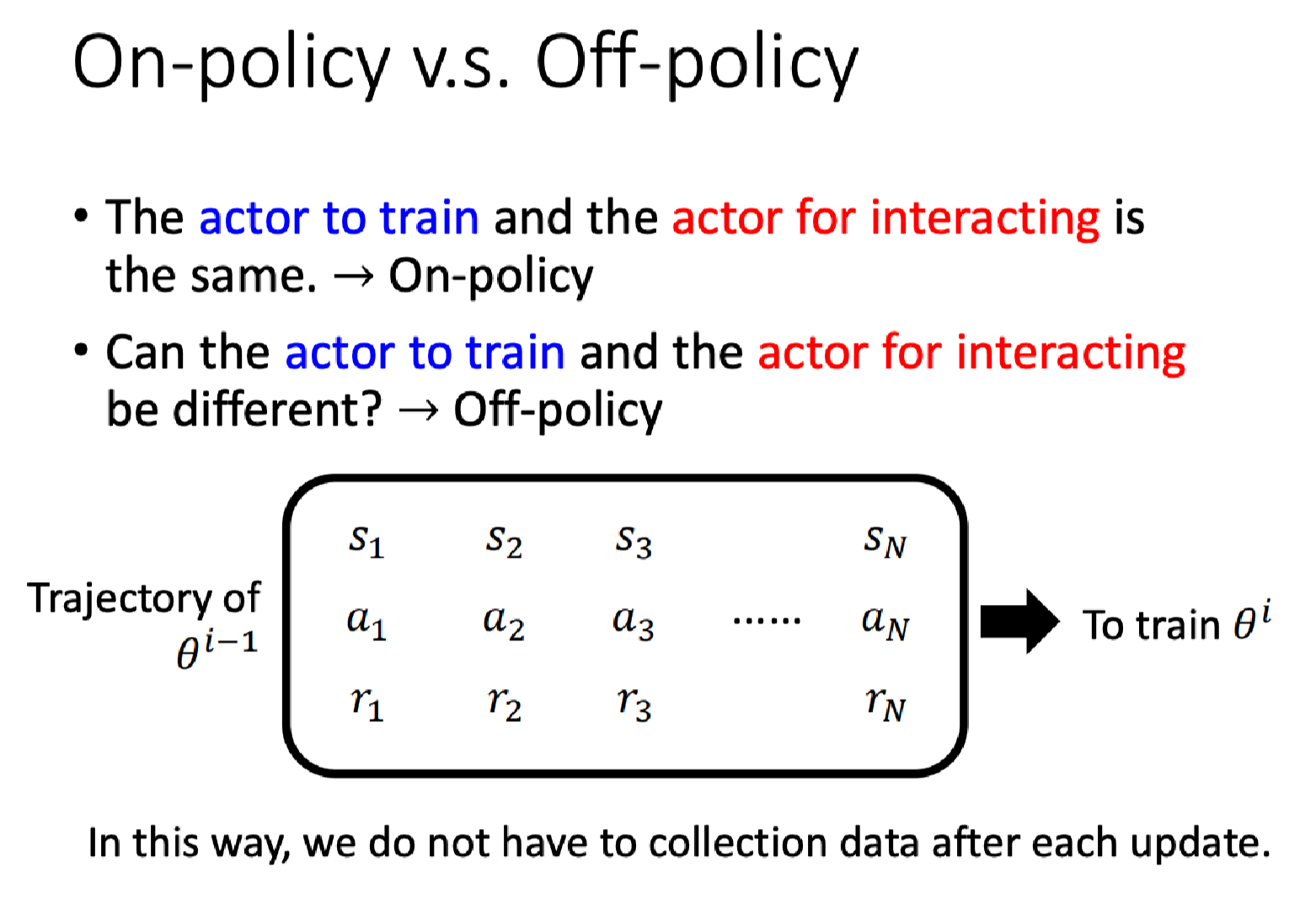
• 同策略(On-policy) 要训练的actor和交互的actor是同一个；
• 异策略(Off-policy) 要训练的actor和交互的actor不是同一个；

刚才我们介绍的是同策略的方法，其实还有一种是异策略的方法，用${\theta }^{i-1}$收集的数据来训练${\theta }^i$。后者有一个显著的优势是我们不必在每次更新后重新收集数据。

近端策略优化(PPO)

异策略的重点是知道自己(actor)和别人(interact)的差距。

PPO后面再学习。

探索

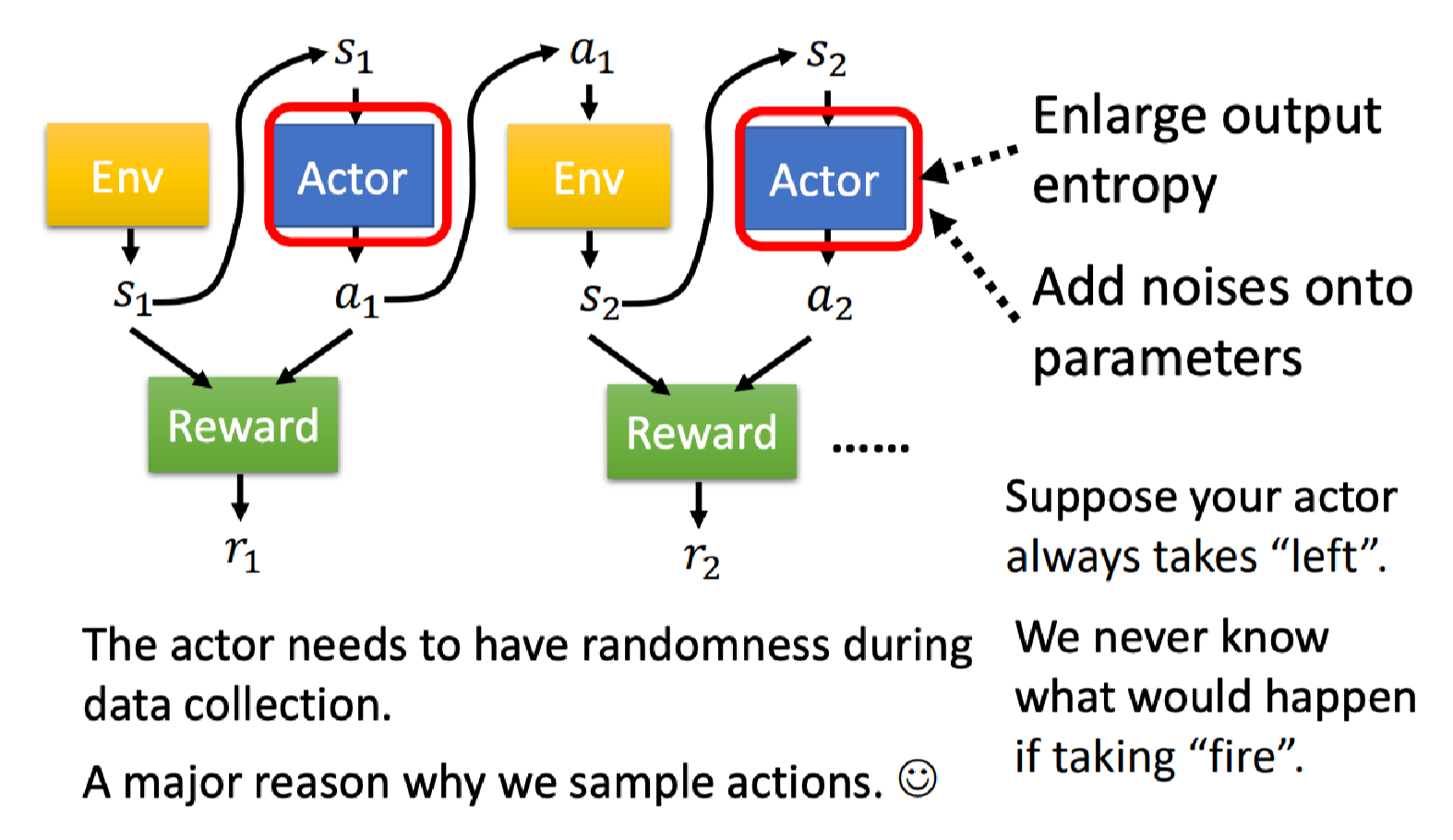
强化学习有一个重要的概念是探索(Exploration)，我们上面说采取行为的时候是需要一些随机性的，这个随机性非常重要。

假设你初始的Actor只会向右移动，永远不知道开火后会发生什么。只有某个Actor执行了开火动作，它才会知道原来开火可以得到更大的奖励，甚至才可以实现最终赢得游戏。

因此在训练时和环境互动的Actor本身的随机性非常重要，甚至此时的随机性要大一点我们才可以收集到比较丰富的数据。才不会有一些状态-动作的奖励从来都不知道。