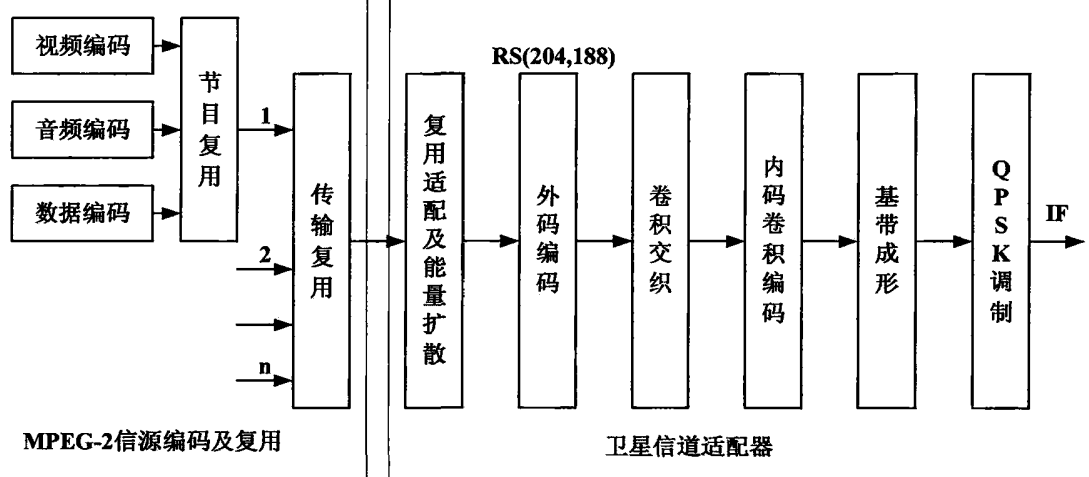
DVB-S系统用于卫星电视信号传输,发送端框图如下所示
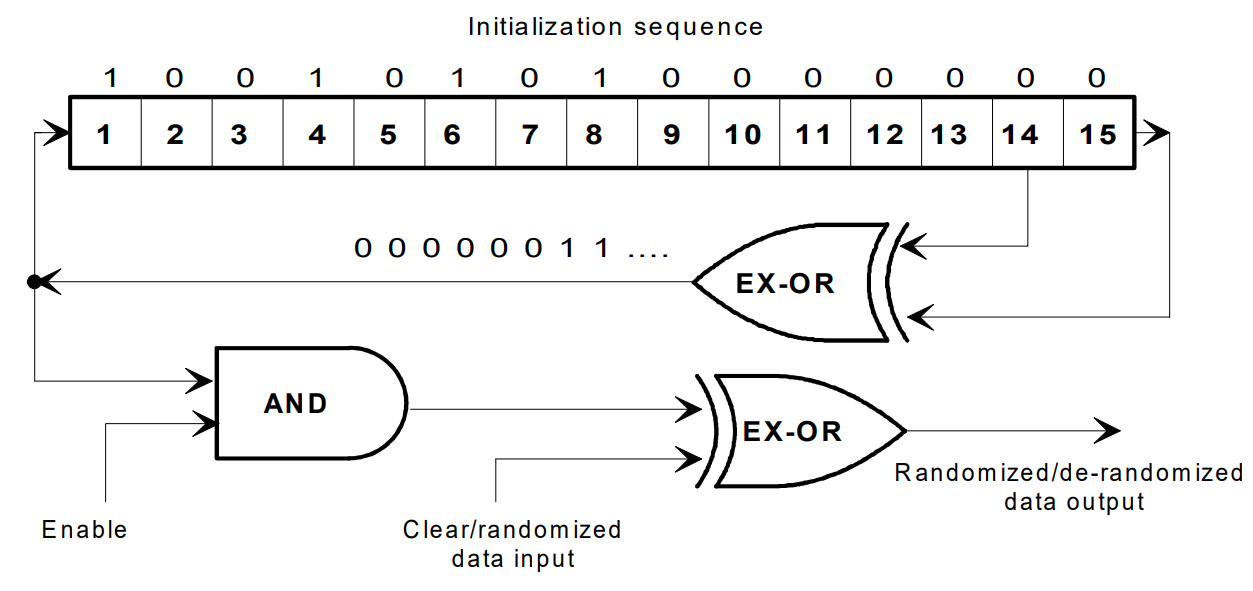
扰码
实际数字通信中,载荷数据的码元会出现长连0或长连1的情况,不利于接收端提取时钟信号,同时会使得数据流中含有大量的低频分量,使得QPSK调制器的相位长时间不变,使得信号易受干扰。因此要对载荷数据进行随机化扰码处理
DVB-S标准中规定扰码的生成多项式为
p ( x ) = x 15 + x 14 + 1 p(x)=x^{15}+x^{14}+1 p(x)=x15+x14+1
同时移位寄存器的初始状态为"1001_0101_0000_000”
Matlab代码仿真
n=500;
% origin_data=randi([0 1],n,1);
origin_cnt_1=nnz(origin_data==1)
scrambling = comm.Scrambler("CalculationBase",2,"InitialConditions",[1 0 0 1 0 1 0 1 0 0 0 0 0 0 0], ...
"Polynomial",[1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1]);
scrambling_data=step(scrambling,origin_data);
scrambling_data_cnt_1=nnz(scrambling_data==1)
运行结果如下图所示

可以看出初始的500点长度的数据包中有403个“1”,经过扰码处理后“1”的个数接近数据总量的一半
外码纠错编码(RS编码)
RS码定义:
G F ( q ) 上( q ≠ 2 , 通常 q = 2 m ),码长 n = q − 1 的本原 B C H 码 GF(q)上(q \neq 2, 通常q=2^m),码长n=q-1的本原BCH码 GF(q)上(q=2,通常q=2m),码长n=q−1的本原BCH码
能纠正 t 个错误的RS码的参数为
- 分组长度n=q-1
- 校验符号数n-k=2t
- 码的最小距离dmin=2t+1
DVB-S系统中使用的RS(188,204)是由RS(239,255)截断而来的,可以纠正8个字节的错误
Matlab仿真
m=8; %bit per symbol
n=204;
k=188;
data_test=randi([0,n],1,k);
data_gf=gf(data_test,m);
data_rs_enc=rsenc(data_gf,n,k);
data_enc=data_rs_enc.x;
data_rs_dec=rsdec(data_rs_enc,n,k);
data_dec=data_rs_dec.x;
subplot(3,1,1);
stem(data_test);
subplot(3,1,2);
stem(data_enc);
subplot(3,1,3);
stem(data_dec);
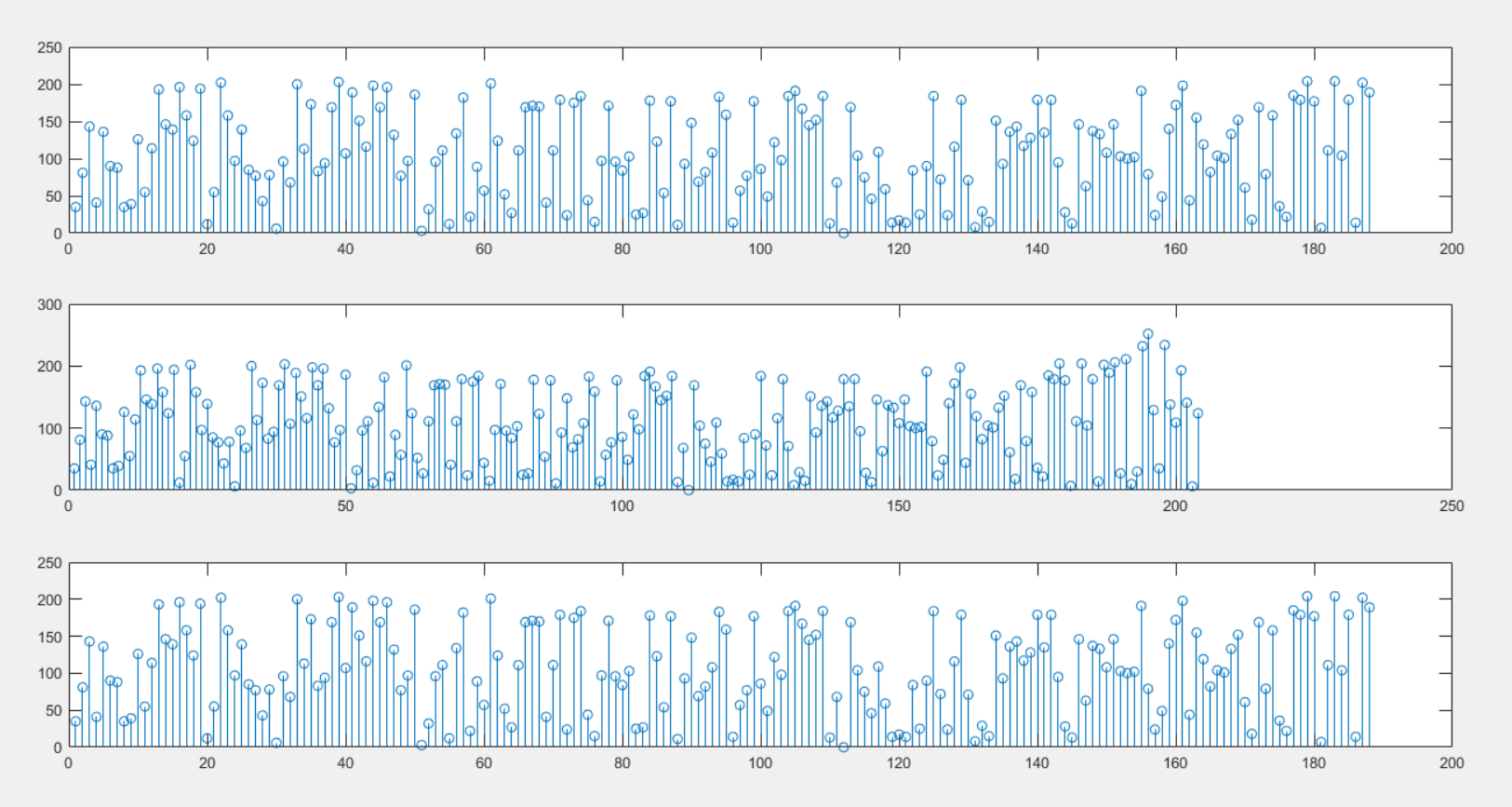
首先生成一个长度为188的序列,将其转换到伽罗华域后,使用rsenc函数进行RS编码,再进行译码,根据对比可以看出译码后的比特和译码前的完全一样
卷积交织
在实际的传输过程中,由于脉冲干扰、多径效应等因素会带来持续一定时间的突发错误,虽然RS码对突发错误有较好的纠错能力,但是当其持续时间较长时,就会超出RS码的纠错能力,因此在编码过程中引入了卷积交织,将数据的传输顺序按照一定的规律分散开,就可以使得错误的码元也被分散开
DVB-S中交织深度为12,总共17个FIFO,数据按行写入寄存器,按列读出
交织后最大可纠错长度为12*8=96
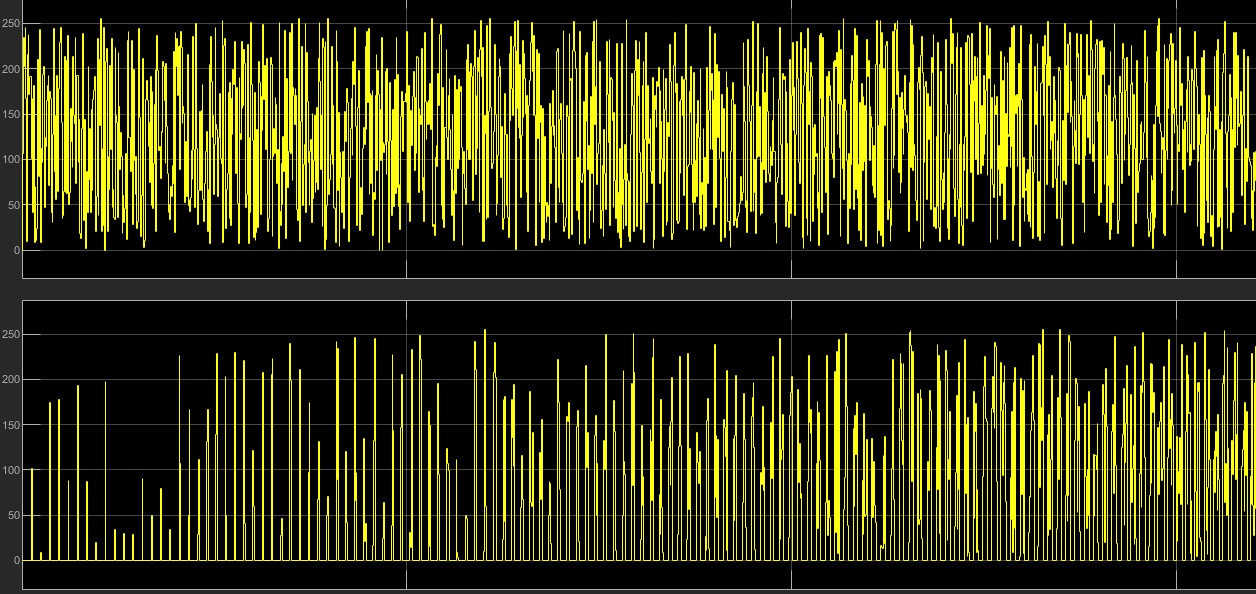
可以看出前一段时间读取到了很多0,说明下面的移位寄存器中的数据还没有移动到末端
卷积编码
卷积码是一种有效的前向纠错码记作 ( n , k , m ) (n,k,m) (n,k,m),将k个信息比特编为n个比特,m为编码存储长度,N=m+1为约束长度,即卷积码的当前码元不仅与当前输入的k的信息码元有关,还与前面m个时刻输入的信息码元有关
clc;
close all;
n=500;
tre1=[1 1 1 1 0 0 1]; %oct 171
tre2=[1 0 1 1 0 1 1]; %oct 133
trellis = poly2trellis(7,[171 133]);
convData=convenc(scrambling_data,trellis);
decData=vitdec(convData,trellis,499,"trunc","hard");
subplot(3,1,1);
stem(scrambling_data);
subplot(3,1,2);
stem(convData);
subplot(3,1,3);
stem(decData);
biterr(scrambling_data,decData)
使用poly2trellis将卷积编码多项式转换为网格描述
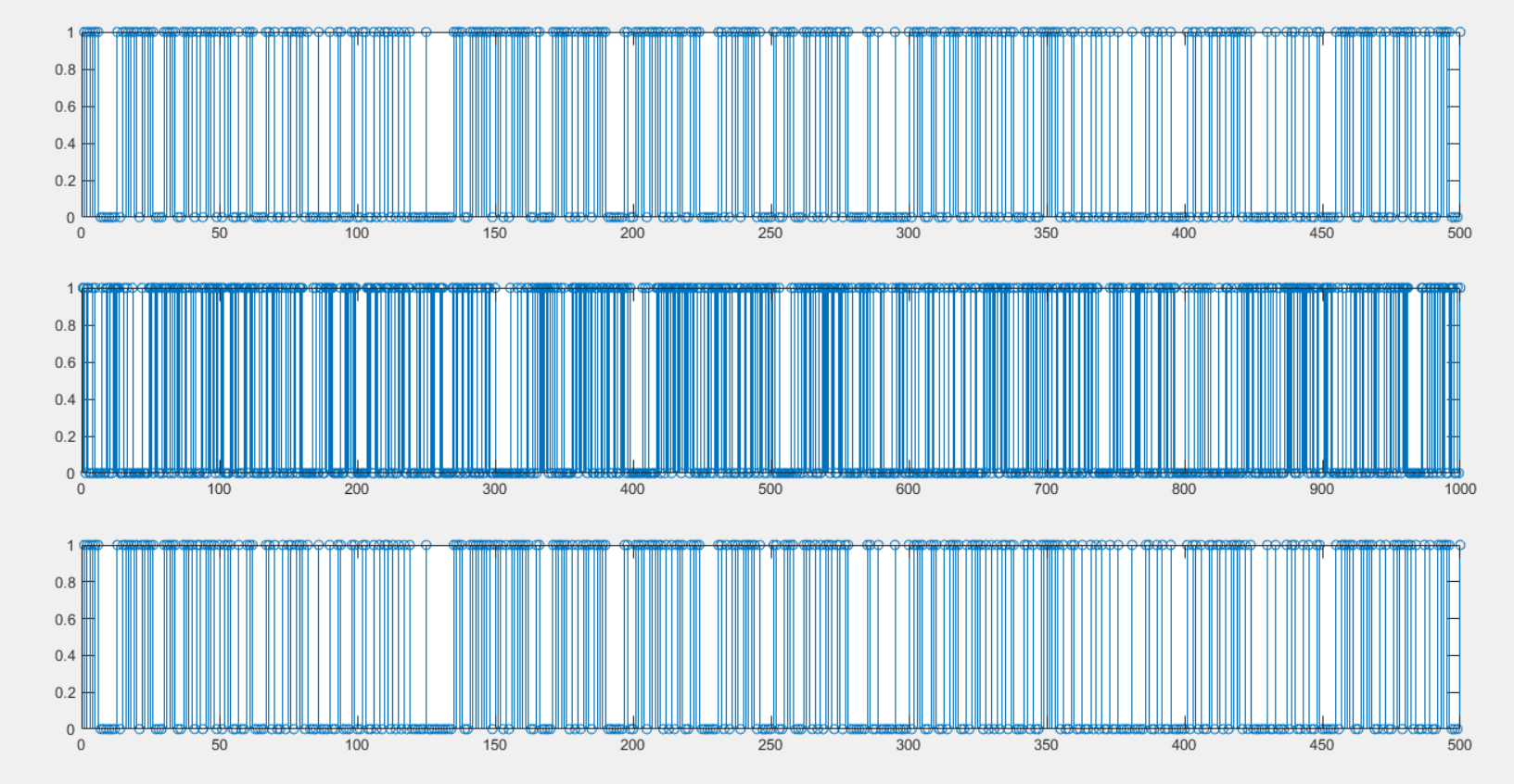
比对后可以看到解码出的数据和原数据完全相同