一维前缀和[模板]

一、题目描述

OJ题目链接：【模板】前缀和_牛客题霸_牛客网

二、思路解析

三、代码

#include <iostream>
using namespace std;
const int N = 100010;
long long arr[N], dp[N];
int n, q;
int main()
{
    cin >> n >> q;
    // 读取数据
    for(int i = 1; i <= n; i++) cin >> arr[i];
    // 处理前缀和数组
    for(int i = 1; i <= n; i++) dp[i] = dp[i - 1] + arr[i];
    while(q--)
    {
        int l, r;
        cin >> l >> r;
        // 计算区间和
        cout << dp[r] - dp[l - 1] << endl;
    }
    return 0;
}

二维前缀和[模板]

一、题目描述

OJ题目链接：【模板】二维前缀和_牛客题霸_牛客网

二、思路解析

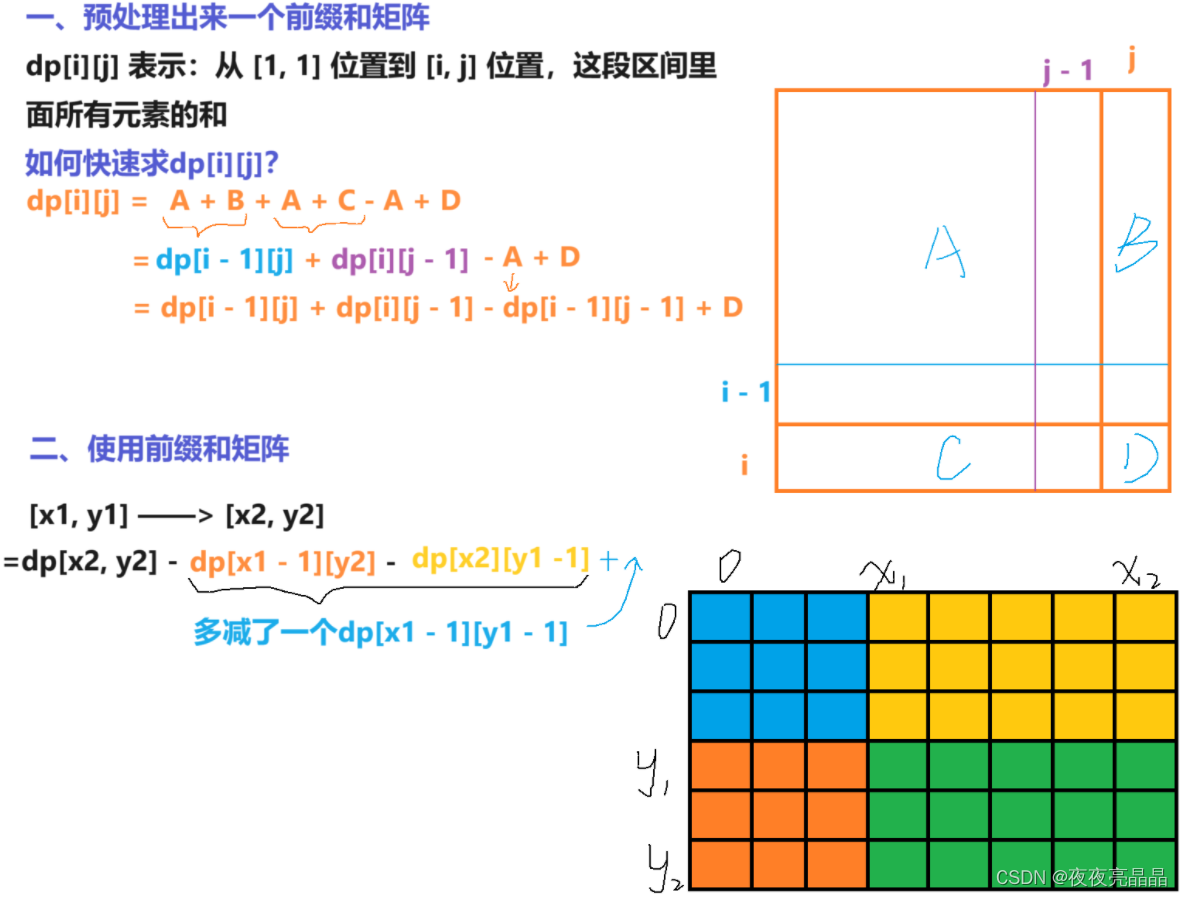
三、代码

#include <iostream>
#include<vector>
using namespace std;
int main() 
{
    int n = 0, m = 0, q = 0;
    cin >> n >> m >> q;
    vector<vector<int>> arr(n + 1, vector<int>(m + 1));
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m ; j++) {
            cin >> arr[i][j];
        }
    }

    vector<vector<long long>> dp(n + 1, vector<long long>(m + 1));
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m ; j++) {
            dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + arr[i][j];
        }
    }

    int x1 = 0, y1 = 0, x2 = 0, y2 = 0;
    while(q--)
    {
        cin >> x1 >> y1 >> x2 >> y2;
        cout << dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1] << endl;
    }
    return 0;
}

724.寻找数组的中心下标

一、题目描述

OJ题目链接：力扣（LeetCode）

二、思路解析

三、代码

class Solution {
public:
    int pivotIndex(vector<int>& nums) 
    {
        int n = nums.size();
        vector<int> dp(n + 1);
        for(int i = 1; i <= n; i++)
        {
            dp[i] = dp[i - 1] + nums[i - 1];
        }
        for(int m = 1; m <= n; m++)
        {
            if(dp[m - 1] == dp[n] - dp[m]) return m - 1;
        }
        return -1;
    }
};

238.除自身以外数组的乘积

一、题目描述

OJ题目链接：力扣（LeetCode）

二、思路解析

三、代码

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) 
    {
        int n = nums.size();
        vector<int> f(n);
        vector<int> g(n);
        vector<int> answer(n);
        f[n - 1] = 1, g[0] = 1;
        for(int i = n - 2; i >= 0; i--)
            f[i] = f[i + 1] * nums[i + 1];
        for(int i = 1; i < n; i++)
            g[i] = g[i - 1] * nums[i - 1];
        for(int i = 0; i < n; i++)
            answer[i] = f[i] * g[i];
        return answer;
    }
};