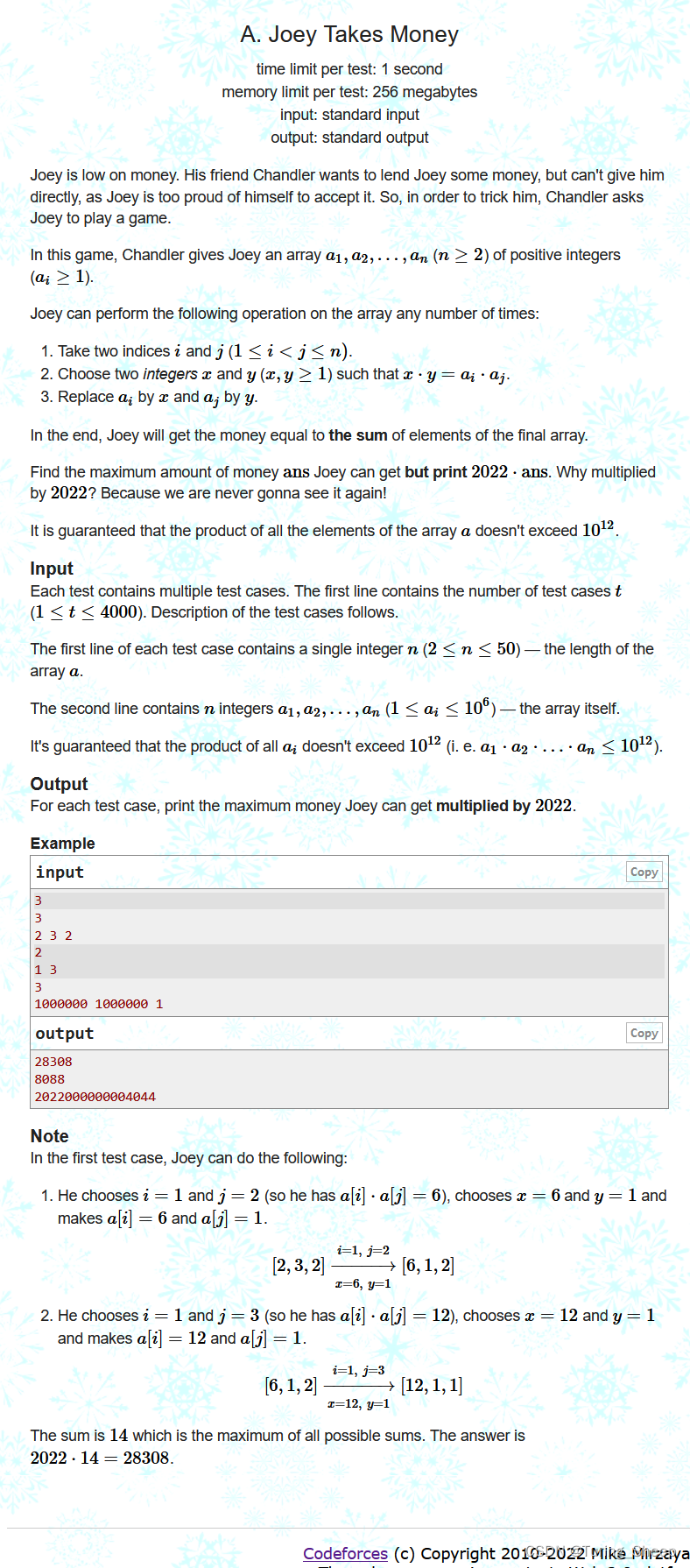
A、 Joey Takes Money

1、题目

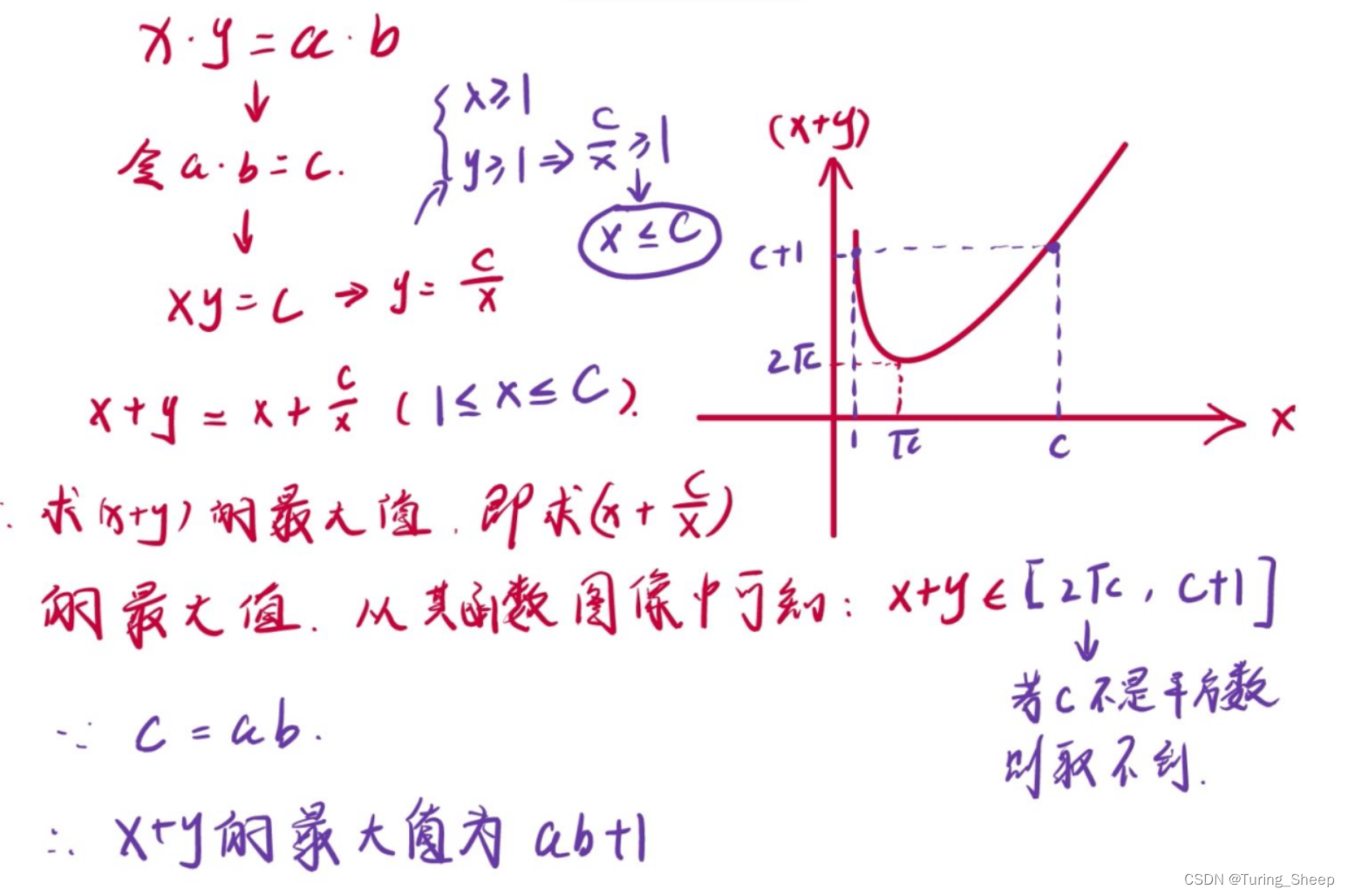
在这里插入图片描述

2、思路

在这里插入图片描述

3、代码

    #include<iostream>
    #include<algorithm>
    #include<cstring>
    using namespace std;
    typedef unsigned long long ll;
    int main()
    {
        ll t;
        cin>>t;
        while(t--)
        {
            int n;
            cin>>n;
            ll sum=1;
            for(int i=0;i<n;i++)
            {
                ll a;
                cin>>a;
                sum*=a;
            }
            ll ans=(sum+(n-1))*2022;
            cout<<ans<<endl;
        }
        return 0;
    }

B、Kill Demodogs

1、题目

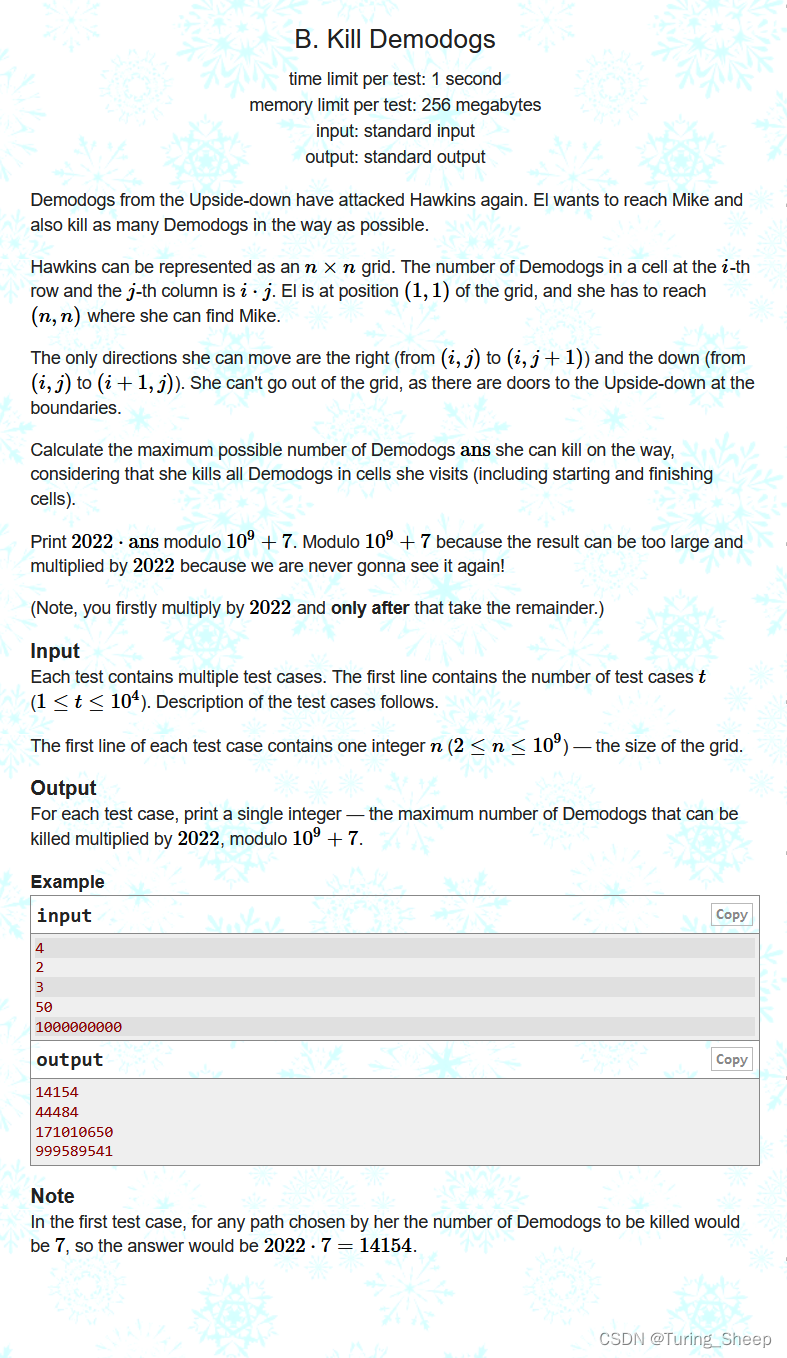
在这里插入图片描述

2、思路（数列、费马小定理、快速幂）

在这里插入图片描述

3、代码

    #include<iostream>
    #include<algorithm>
    #include<cstring>
    using namespace std;
    const int mod=1e9+7;
    typedef unsigned long long ll;
    ll qmi(ll a,ll b,ll p)
    {
        ll res=1;
        while(b)
        {
            if(b%2)res=res*a%p;
            a=a*a%p;
            b/=2;
        }
        return res%p;
    }                                          
    int main()
    {
        int t;
        cin>>t;
        while(t--)
        {
            ll n;
            cin>>n;
            ll sum=0;
            sum=(ll)n*(n+1)%mod*(4*n-1)%mod*qmi(6,mod-2,mod)%mod*2022%mod;
            cout<<sum<<endl;
        }
        return 0;
    }

C、Even Subarrays

1、题目

在这里插入图片描述

2、思路（前缀异或和）

首先对于异或的性质我们要有个了解。如果A异或B等于C的话，那么必定满足B^C等于A，A异或C等于B。

涉及到区间问题，我们这里使用前缀异或和。

这道题中所提到的因子个数是奇数，那么必定是一个完全平方数。所以我们只需要找到异或区间内所有数字异或的结果是完全平方数的即可。然后我们利用总的数目减去不符合条件的数目。
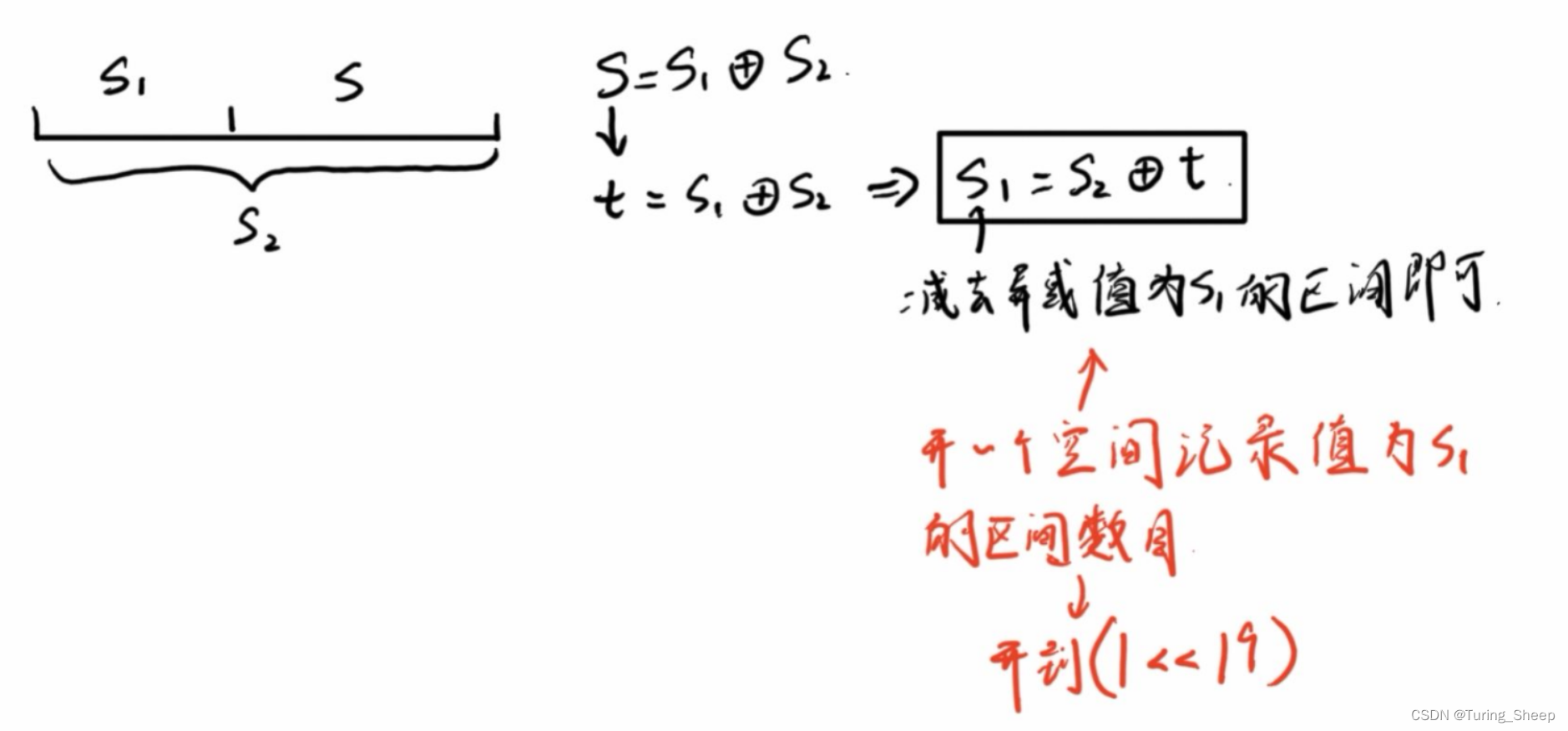
在这里插入图片描述

现在的问题有两个，我们如何计算总的数目？我们如何排除不符合条件的情况？
我们看下面的推导：
异或区间总数目：
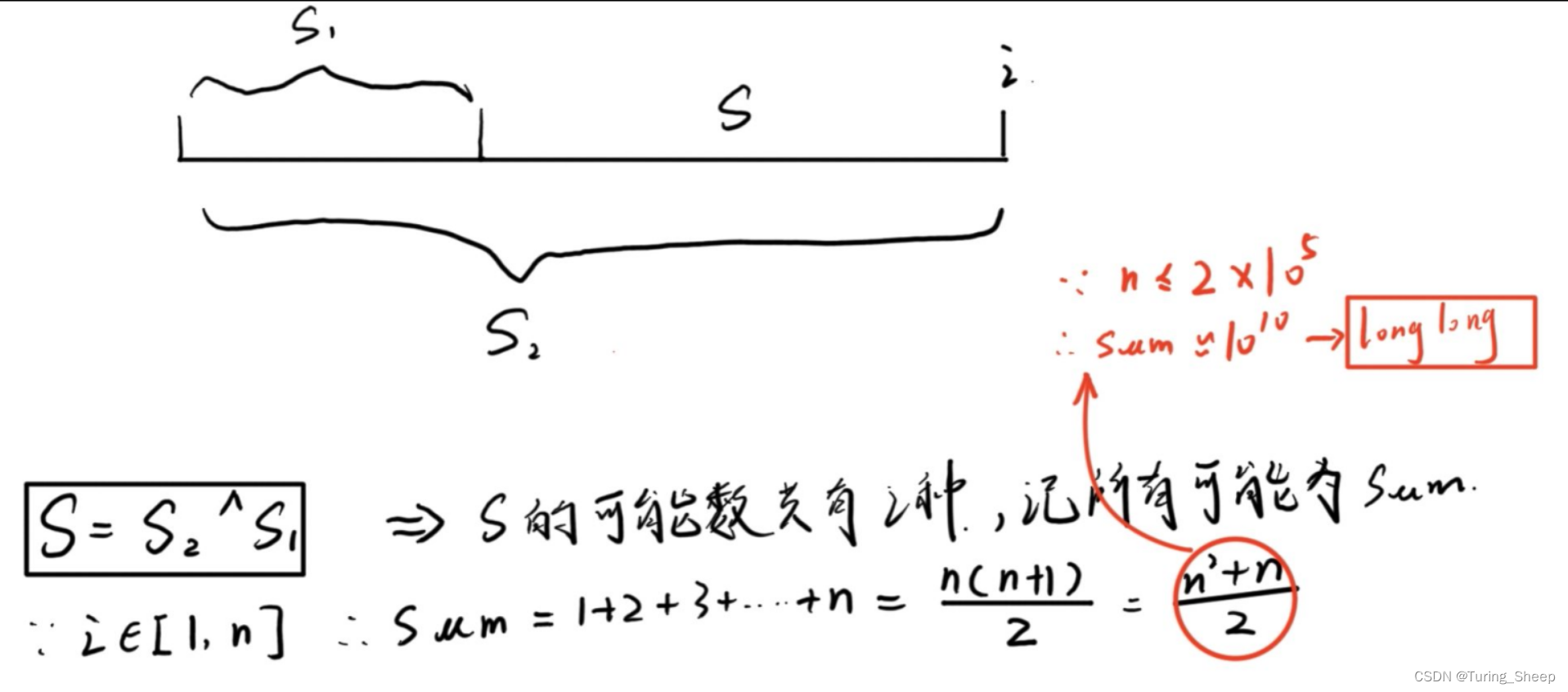
在这里插入图片描述
平方数记作 $t$ (不是题干中的t)，下面推导这个平方数的所在范围。

知道了这个t的范围之后，我们只需要去枚举他的开方情况即可。这样可以降低时间复杂度。

那么总的思路如下图：
在这里插入图片描述枚举所有的S2，然后枚举平方数t，计算出S1，减去所有等于S1的情况。

那么总的时间复杂度就是 $O(n\sqrt{n})$

3、代码

    #include<iostream>
    #include<cstring>
    #include<algorithm>
    using namespace std;
    const int N=4e6+10;
    typedef long long ll;
    int a[N],cnt[N];
    int t,n;
    int main()
    {
        cin>>t;
        while(t--)
        {
            cin>>n;
            int ma=2*n;
            for(int i=1;i<=n;i++)
            {
                scanf("%d",a+i);
                a[i]^=a[i-1];
            }
            ll ans=0;
            cnt[a[0]]++;
            for(int i=1;i<=n;i++)
            {
                ans+=i;
                for(int j=0;j*j<=ma;j++)
                {
                    ans-=cnt[a[i]^(j*j)];
                }
                cnt[a[i]]++;
            }
            for(int i=1;i<=ma;i++)
                cnt[a[i]]=0;
            cout<<ans<<endl;        
        }
        return 0;
    }

D、Valiant’s New Map

1、题目

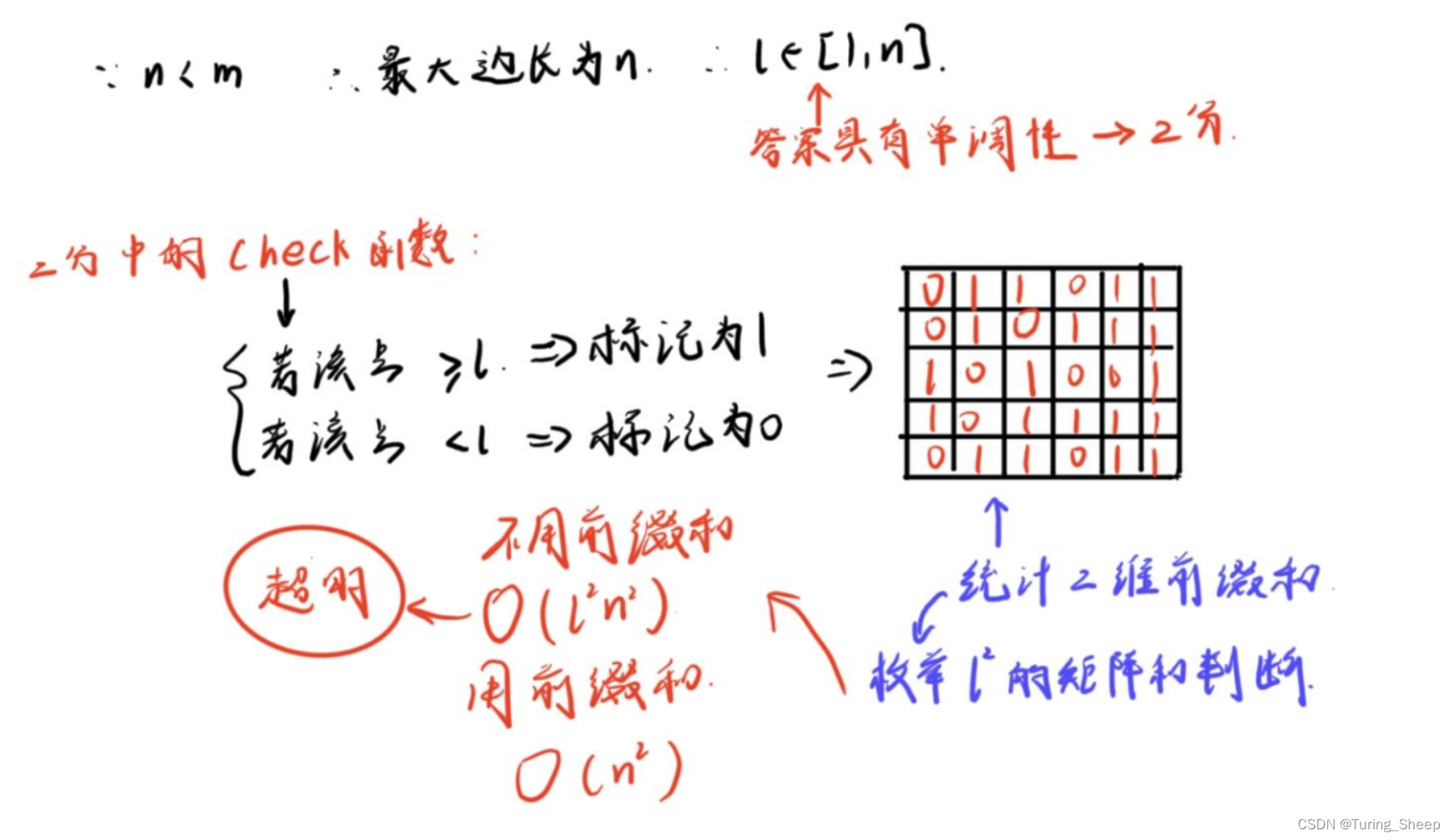
在这里插入图片描述

2、思路（二分、二维前缀和）

思路很简单，二分找答案，前缀和判断。
在这里插入图片描述

3、代码

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
const int N=1e6+10;
int n,m;
bool check(int x,vector<vector<int>>&a,vector<vector<int>>&g)
{
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            a[i][j]=a[i-1][j]+a[i][j-1]-a[i-1][j-1]+(int)(g[i][j]>=x);
    for(int i=x;i<=n;i++)
    {
        for(int j=x;j<=m;j++)
        {
            int res=a[i][j]-a[i-x][j]-a[i][j-x]+a[i-x][j-x];
            if(res==x*x)return true;
        }
    }
    return false;
}
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        cin>>n>>m;
        vector<vector<int>>a(n+1,vector<int>(m+1));
        vector<vector<int>>g(n+1,vector<int>(m+1));
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
                scanf("%d",&g[i][j]);
        int l=1,r=n;
        while(l<r)
        {
            int mid=l+r+1>>1;
            if(check(mid,a,g))l=mid;
            else r=mid-1;
        }
        cout<<l<<endl;
    }
    return 0;
}