1. 范数的意义
范数可以简单的理解为“距离”。由于向量是既有大小又有方向的量,所以向量是不能直接比较大小的,但是范数提供了一种方法,可以将所有的向量转化为一个实数,然后就可以比较向量的大小了。(注:本文我们只讨论向量范数,向量范数表征向量空间中向量的大小,另一种叫矩阵范数,表征矩阵引起变化的大小。本文地址:https://blog.csdn.net/bluishglc/article/details/128642156,转载请注明出处)
2. 范数的计算方法
范数并不是一个数,而是一组数,我们先了解一下最常用的L-2范数范数,它的计算方法是:将向量的每一个分量平方后再求和,然后对和开平方,得到的就是这个向量的L-2范数范数了,使用公式描述就是:
- L-2范数

其中x1到xn是向量中的每一个分量。L-2范数范数度量的是向量到原点的距离,这个距离正是向量的“模”(Magnitude)(“模”指的就是向量的长度)。我们将在后面深入介绍L-2范数及其应用。
- L-1范数
L1型范数的就是所有元素的绝对值之和。对于L-1范数的应用我们留待以后介绍。

- L-P范数
前面说过:范数并不是一个数,而是一组数,这取决于对每一个分量求的是几次方和对和开的几次方根,通用的范数公式是这样:

当P取2时,上述公式就是L-2范数,当P取1时,上述公式就是L-1范数。
3. “两个向量间的”L-2范数
我们说范数度量的是两个向量之间的距离,即:度量的是它们之间的相似程度或者说差异程度,但是从L-2范数的计算公式上可以看出,它只用了一个向量,这个怎么解释呢?其实L-2范数计算的是:向量到原点的距离。我们来看下面这个公式:

这是L-P范数的另一种表述形式,它计算的是两个向量(ax, ay, …, az)和(bx, by, …, bz)之间的距离。为了便于区分,我们把前面的L-2范数公式称为:(单向量)L-2范数公式,前后对比一下就会发现:当P=2,B=(0, 0, …, 0)时,就会“退化”成(单向量)L-2范数公式。所以说:(单向量)L-2范数计算的向前向量和0向量(原点)之间的距离,由于原点处的向量各分量均为0,减与不减没有分别别,所以才看上去只有一个向量参与计算。此外,当P=2时,上述公式计算出的“两个向量间的”距离就是欧式距离!
利用这个可以直接计算两向量间距离的L-2范数公式,我们用一个例子看一下如何计算两个向量间的欧式距离。假设二维平面上有A(2,3)和B(3,1)两个点,如图所示:

A,B同时也是两个向量,套用L-2范数范数计算公式,可以计算出向量A(2,3)的L-2范数范数约为:3.6,这个值也是向量A的模,也就是A点到原点的距离。同理,向量B(3,1)的L-2范数范数约为:3.16。我们现在可以说:向量A(2,3)到0向量(0,0)的距离是3.6,向量B(3,1)到0向量(0,0)的距离是3.16。那向量A到向量B的距离怎么算呢?套用上面的公式,可得结果约为2.236, 计算过程如下:

备注:目前互联网上的文章对标准L-2范数公式没有定论,有的使用是公式1(单向量版本),有的使用的是公式1(两向量差版本),虽然两个公式其实是统一的,但是从NumPy的计算方式来看,计算L-2范数使用的是公式1。
4. 使用NumPy计算范数
虽然范数的计算规则并不复杂,但是对于元素数量较多的向量来说,计算起来还是很麻烦的,为此,NumPy提供了专门用于计算各型范数的函数:numpy.linalg.norm(),官方文档:https://numpy.org/doc/stable/reference/generated/numpy.linalg.norm.html#numpy.linalg.norm,下图解释了该函数3个核心参数的意义:
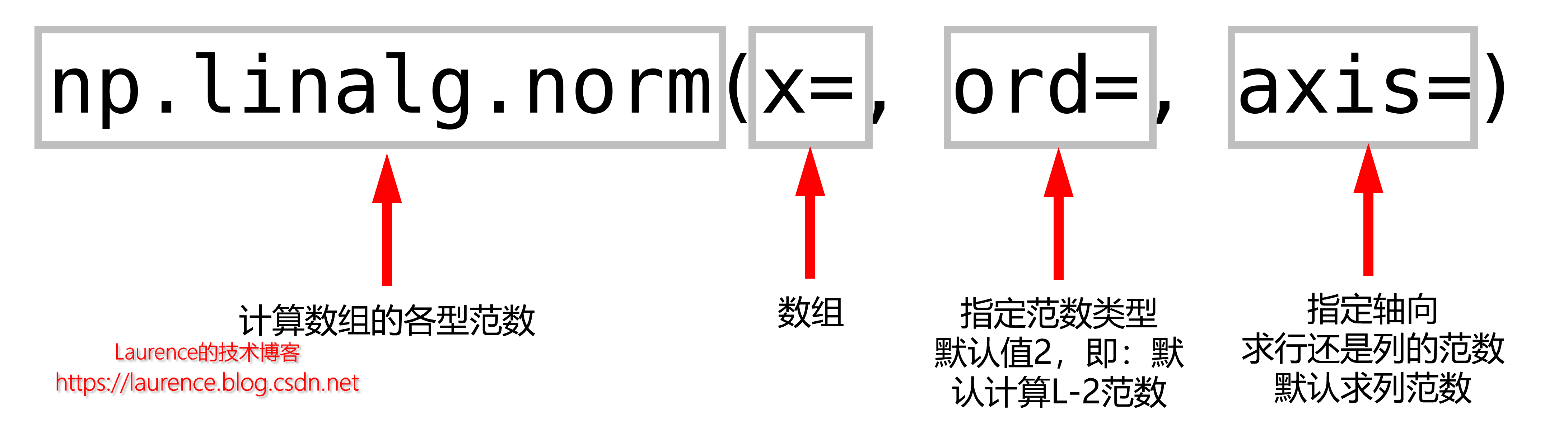
5. 计算(单向量)范数
现在我们就用NumPy的norm函数去计算一个二维数组的L-2范数。在下面的示例代码中,我们没有显式设定ord参数,所以求的是L-2范数。对于axis参数的设置符合NumPy的默认惯例:
- 不设置axis参数是求整个数组(所有元素)的范数
- 显式设置axis=0是求列向量的范数
- 显式设置axis=1是求行向量的范数
import numpy as np
# author: https://laurence.blog.csdn.net/
samples=[[-1, 1, 3],
[-1, 3, 2]]
# 计算列向量的L2范数
samples_norms = np.linalg.norm(samples, axis=0)
print(f"samples norms by column: \n{samples_norms}")
# 计算行向量的L2范数
samples_norms = np.linalg.norm(samples, axis=1)
print(f"samples norms by row: \n{samples_norms}")
# 计算整个二维数组(即所有元素)的L2范数
samples_norms = np.linalg.norm(samples)
print(f"samples norm: \n{samples_norms}")
程序输出:
samples norms by column:
[1.41421356 3.16227766 3.60555128]
samples norms by row:
[3.31662479 3.74165739]
samples norm:
5.0
计算(两向量间的)范数(相似度)
下面我们从单一向量拓展到计算两个向量间的范数。我们就直接借用图1所示的案例,计算向量A(2,3)和B(3,1)间的距离。NumPy并没有直接提供相应的函数,但是这个计算只需拆解为两步就能完成,所以还是非常简单的。首先,向量A(2,3)和B(3,1)间的距离其实就是向量B减去向量A得到的一个差值向量,它的“长度”就是AB间的距离。所以我们只需要求出向量B减去向量A的差值向量,然后用norm函数算出它的l-2范数就可以了。NumPy也为我们直接提供了向量的减法支持,以下是实际代码:
import numpy as np
# author: https://laurence.blog.csdn.net/
A = np.array([2,3])
B = np.array([3,1])
# 使用NumPy数组减法直接求得差向量
AB = B-A
print(f"AB = {AB}")
# 计算差向量的大小(L-2范数),结果就是向量A到向量B的“距离”
# 也就是度量向量A到向量B相似程度的一个数值!
ab_norm = np.linalg.norm(AB)
print(f"Distance between A and B: {ab_norm}")
程序输出:
AB = [ 1 -2]
Distance between A and B: 2.23606797749979
参考:
Normalization using NumPy norm
Vector Norms: quick explanation