动归专题——斐波纳契模型和路径问题

前提

本专题开始，注重整理与动态规划相关的题目，从简单的动归开始切入，慢慢掌握和练习动态规划这一重要的算法思想，部分相对复杂的题目会结合画图和代码分析去解释

一、第N个泰波纳契数列

1.链接

1137. 第 N 个泰波那契数 - 力扣（LeetCode）

2.描述

3.思路

关于动态规划的题目，往后都是按照五步走的统一思路去进行分析

（1）状态表示

状态表示我们通常是根据经验加对具体题目的判断去设置的，通常的设置思路有：

以第i个位置为底，结合题目条件...

以第i个位置开始，结合题目条件...

...

本题状态表示：f（i）表示以i位置为底，泰波那契数列的值

（2）状态转移方程

状态方程的判断一般需要我们根据具体的题目条件去进行推导，这题目的方程式就是状态转移方程

f（i） = f（i-1）+ f(i-2) + f(i-3)

（3）初始化

初始化是为了确定边界条件，确定起始位置

f（0）= 0，f（1）= 1，f（2） = 1；

（4）填表顺序

写代码时，我们需要一个dp表，我们需要根据状态方程去判断填表顺序是从如何推导，本题的推导顺序很明显是从头往后推导记录

（5）返回值

确定返回的值，这个返回值根据题目不同，可能返回的不同，本题是返回dp[ n ]

4.参考代码

class Solution {
public:
    int tribonacci(int n) 
    {
        if(n == 0) return 0;
        if(n == 1 || n == 2) return 1;//考虑边界情况

        vector<int> dp(n+1);//创建dp表
        dp[0] = 0; dp[1] = 1; dp[2] = 1;//确定初始状态

        for(int i = 3;i<=n;i++)
        {
            dp[i] = dp[i-1] + dp[i-2] + dp[i-3];
        }
        return dp[n];
    }
};

二、三步走问题

1.链接

面试题 08.01. 三步问题 - 力扣（LeetCode）

2.描述

3.思路

（1）状态表示

以第n个台阶为底（一共有n个台阶），小孩一共有多少种走法

（2）状态转移方程

dp[ n ] = dp[n - 1] + dp[n - 2] + dp[n - 3]

（3）初始化

dp[1] = 1; dp[2] = 2; dp[3] = 4

（4）填表顺序

从左到右

（5）返回值

dp[ n ]

4.参考代码

class Solution {
public:
    const int num = 1e9+7;
    int waysToStep(int n) 
    {
        if(n == 1 || n == 2) return n;
        if(n == 3) return 4;
        vector<int> dp(n+1);
        dp[1] = 1; dp[2] = 2; dp[3] = 4;
        for(int i = 4;i <= n;i++)
        {
            dp[i] = ((dp[i-1] + dp[i-2])%num + dp[i-3])%num;
        }
        return dp[n];
    }
};

三、使用最小花费爬楼梯

1.链接

746. 使用最小花费爬楼梯 - 力扣（LeetCode）

2.描述

3.思路

（1）状态表示

思路一：以i为结束，...

f（i）表示爬到第i层，花费最少的费用

思路二：以i为开始，...

f（i）表示从第i层开始，到楼顶需要花费最少的费用

（2）状态表示方程

思路一： f（i）= min ( f(i -1)+cost[i-1] ，f(i-2)+cost[i-2] ）

思路二： f（i）= min( f(i+1) , f(i+2) ) + cost [ i ]

（3）初始化

思路一：f（0）= 0 ; f( 1 ) = 0

思路二：f（n）= cost[ n ] ; f（n-1）= cost[n-1]

（4）填表顺序

思路一：从左到右

思路二：从右到左

（5）返回值

思路一：dp[n]

思路二：dp[0]

4.参考代码

思路一：

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) 
    {
        vector<int> dp(cost.size()+1);
        dp[0] = 0;
        dp[1] = 0;

        for(int i = 2;i<=cost.size();i++)
        {
            dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
        }
        return dp[cost.size()];
    }
};

思路二：

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) 
    {
        int n = cost.size()-1;
        vector<int> dp(n+1);
        dp[n] = cost[n];
        dp[n-1] = cost[n-1];

        for(int i = n-2;i>=0;i--)
        {
            dp[i] = min(dp[i+1],dp[i+2])+cost[i];
        }
        return min(dp[0],dp[1]);
    }
};

四、解码方法

1.链接

. - 力扣（LeetCode）

2.描述

3.思路

4.参考代码

class Solution 
{
public:
    int numDecodings(string s) 
    {
        int n = s.size();
        //由于dp[0]要作为辅助位置，因此映射关系整体向后移
        //也可以认为此刻dp[i]对应的就是从1开始往后数的第i个字母
        vector<int> dp(n+1,0);
        dp[0] = 1;
        dp[1] = s[0] != '0';
        for(int i = 2;i<=n;i++)
        {
            if(s[i-1]!='0')//i位置的数字单独解码成功
                dp[i]+=dp[i-1];

            int second = (s[i-2]-'0')*10+(s[i-1]-'0');
            if(second>=10 && second<=26)//第二种情况解码成功
                dp[i]+=dp[i-2];
        }
        return dp[n];
    }
};

五、不同路径

1.链接

62. 不同路径 - 力扣（LeetCode）

2.描述

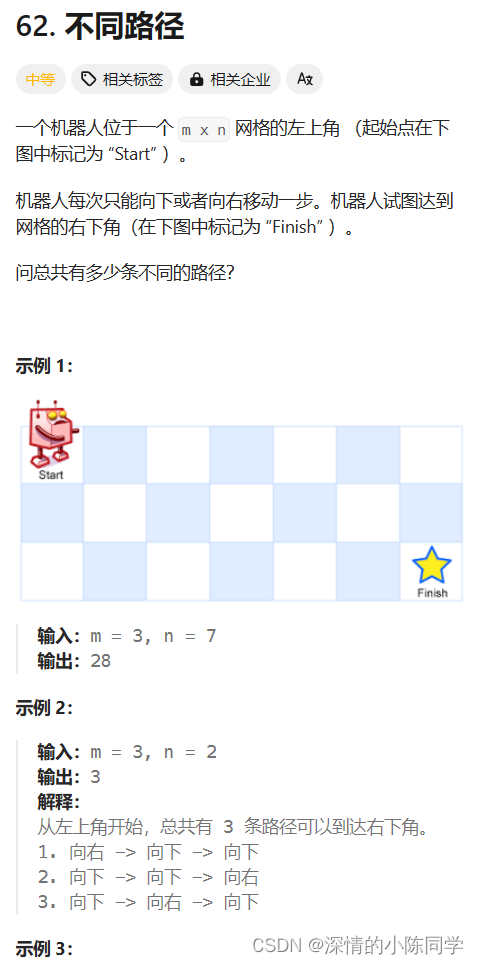
3.思路

（1）状态表示

从左上角出发，走到[ i , j ]位置时一共有dp（i，j）种办法

（以[i,j]为结束，...）

（2）状态表示方程

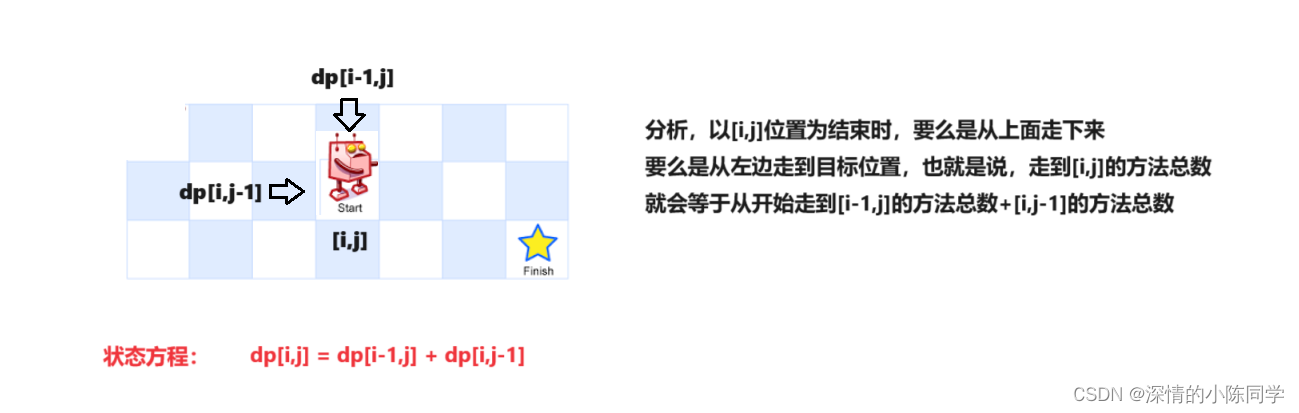
（3）初始化

初始化需要考虑边界问题，通常我们会选择给路径多加上一层边框，然后对边框进行合理的赋值

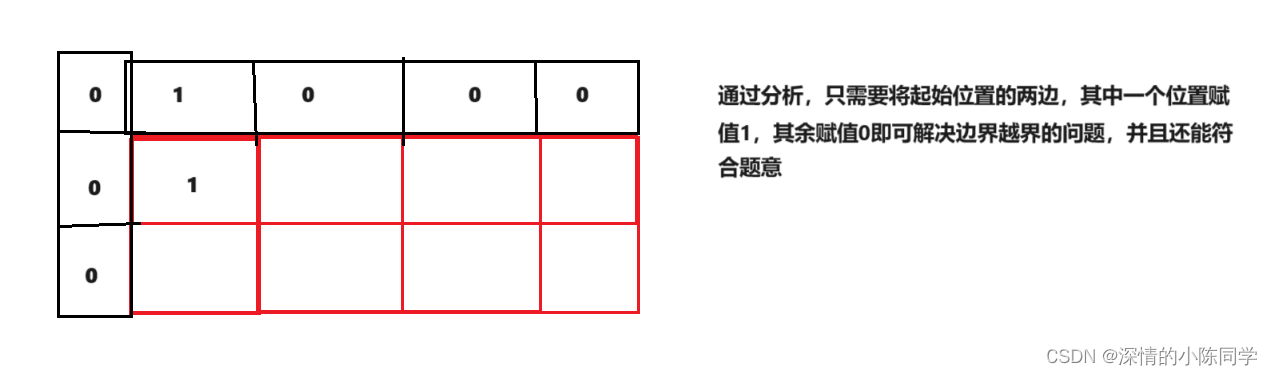
（4）填表顺序

从左到右，从上到下，就是遍历二维数组的顺序

（5）返回值

dp[m,n]

4.参考代码

class Solution {
public:
    int uniquePaths(int m, int n) 
    {
        vector<vector<int>> dp(m+1,vector(n+1,0));
        dp[0][1] = 1;
        for(int i =1;i<=m;++i)
        {
            for(int j = 1; j<=n;++j)
            {
                dp[i][j] = dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[m][n];
    }
};

六、不同路径||

1.链接

63. 不同路径 II - 力扣（LeetCode）

2.描述

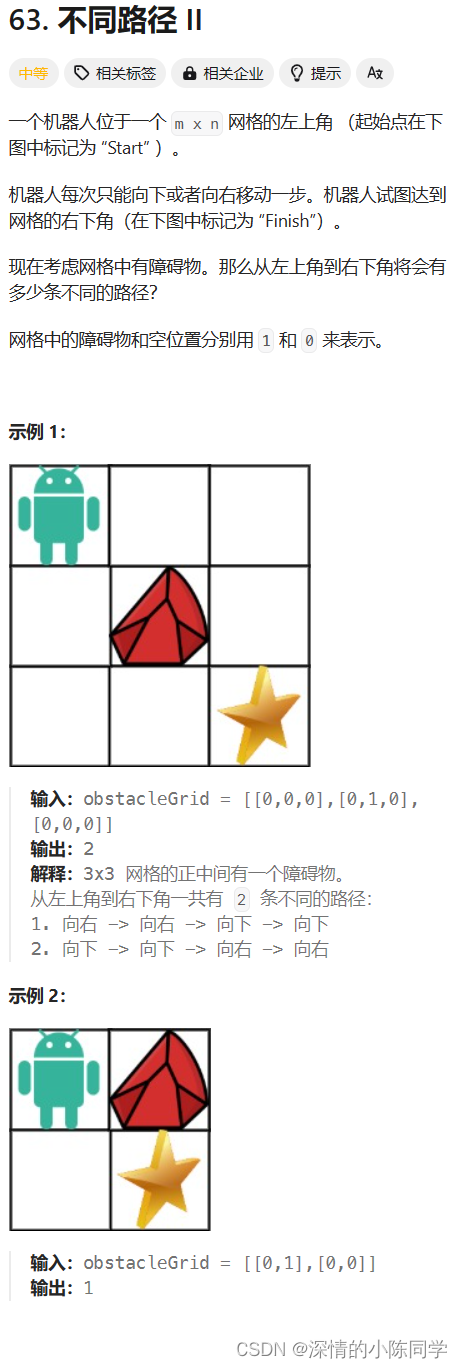
3.思路

（1）状态表示

dp[i,j] : 以[i,j]位置结束，一共有dp[i,j]种路线

（2）状态表示方程

（3）初始化

和上题的初始化一样，不过这里就需要注意映射关系了，在题目给的障碍表格中要注意映射关系

（4）填表顺序

从左上角到右下角

（5）返回值

dp[m,n]

4.参考代码

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) 
    {
        int m = obstacleGrid.size();
        int n = obstacleGrid[0].size();
        vector<vector<int>> dp(m+1,vector(n+1,0));
        dp[0][1] = 1;
        for(int i = 1;i<=m;i++)
        {
            for(int j = 1;j<=n;j++)
            {
                if(obstacleGrid[i-1][j-1] != 1)
                {
                    dp[i][j] = dp[i-1][j] + dp[i][j-1];
                }
            }
        }
        return dp[m][n];
    }
};

七、珠宝的最高价值

1.链接

LCR 166. 珠宝的最高价值 - 力扣（LeetCode）

2.描述

3.思路

（1）状态表示

dp[i,j] 表示以[i,j]位置结束，所获得的最大珠宝价值

（2）状态表示方程

有了上面两题的经验，不难分析出，[i,j]位置获得的最大珠宝价值，会等于当前位置的珠宝价值加上max（dp[i-1,j]，dp[i,j-1]）

dp[i,j] = max（dp[i-1,j]，dp[i,j-1]）+frame[ i ][ j ] （实际代码中要注意具体映射位置）

（3）初始化

和前两题一样的初始化方式，但是本题中不需要对第一个位置进行赋值为1，因为此时dp记录的是珠宝的价值，因此起始是不需要赋值的，全部初始化为0即可

（4）填表顺序

从左上角到右下角

（5）返回值

return dp[m][n]

4.参考代码

class Solution {
public:
    int jewelleryValue(vector<vector<int>>& frame) 
    {
        int m = frame.size();
        int n = frame[0].size();
        vector<vector<int>> dp(m+1,vector(n+1,0));
        for(int i = 1;i<=m;i++)
        {
            for(int j = 1;j<=n;j++)
            {
                dp[i][j] = max(dp[i-1][j],dp[i][j-1])+frame[i-1][j-1];
            }
        }
        return dp[m][n];
    }
};

八、下降路径最小和

1.链接

931. 下降路径最小和 - 力扣（LeetCode）

2.描述

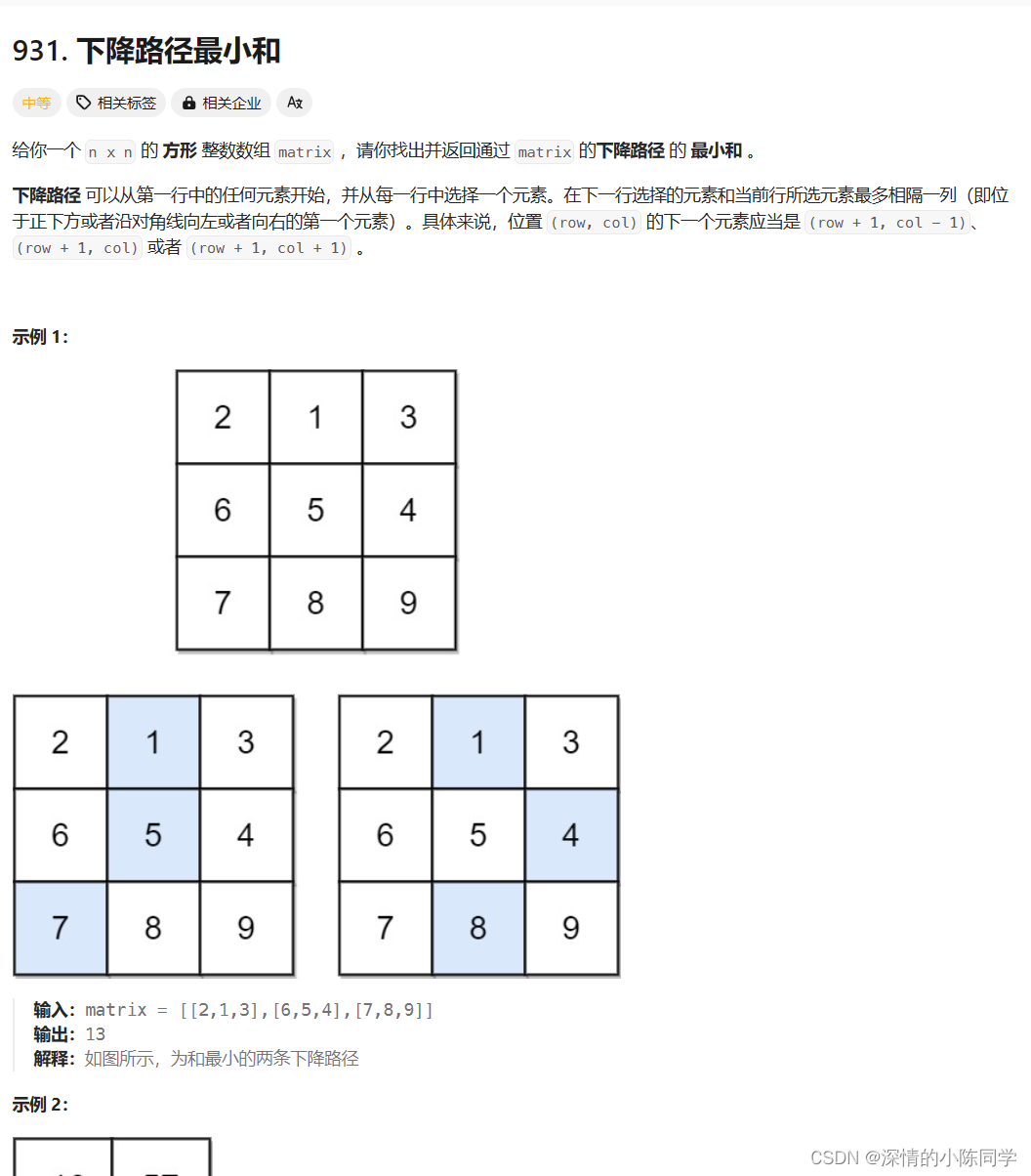
3.思路

（1）状态表示

这次我们换一个思路，“以i位置开始，...”

以当前位置[ i ][ j ] 开始，走到最底下的最小路径和为dp[ i ][ j ]

（2）状态表示方程

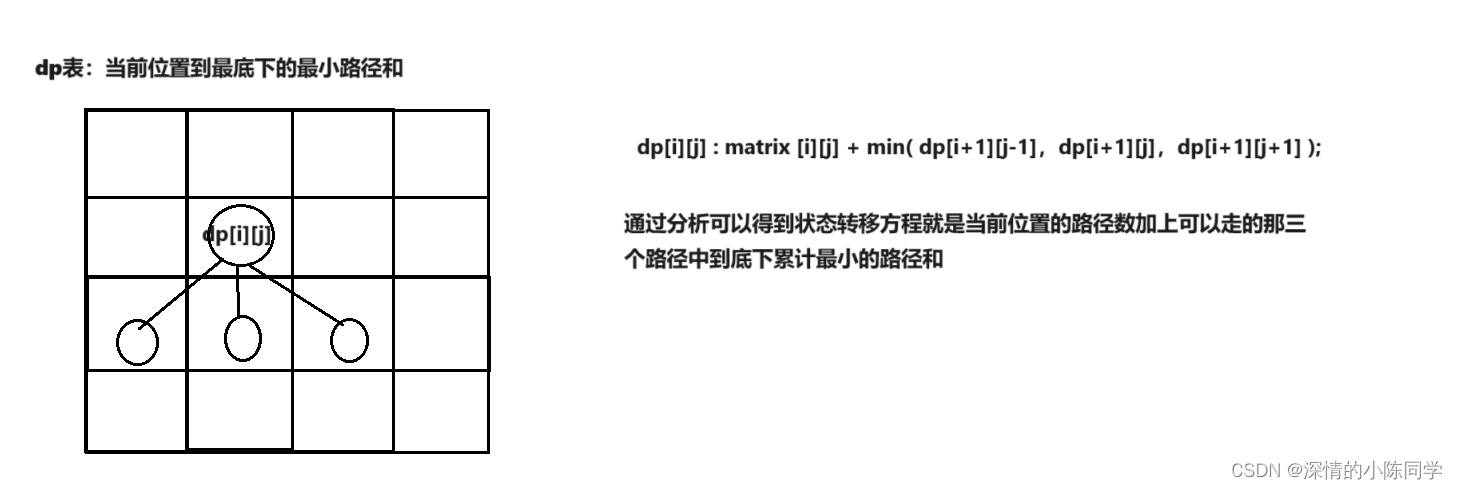
（3）初始化

我们通过题目可以看到，每次dp遍历选择时，最左边那一列和最右边那一列存在越界的问题，因此我们可以给左右两边各加上一列去解决边界越界的问题，同时由于题目计算的是最小路径和，辅助列相当于非法路径，我们可以给其赋值为最大值，即可保证dp不会选择非法路径，再往最后一行添加一行辅助行，实现最后一列dp的赋值

（4）填表顺序

从最后一行往上填表,从下到上，从左往右

（5）返回值

取第一行中最小值返回

4.参考代码

这种思路到这来在映射关系上会比较复杂，需要画图，这题是为了练习另一种思路，推荐使用：

以[i][j]位置结束，所需的最小路径和为dp[i][j]的思路会更好写代码

class Solution {
public:
    int minFallingPathSum(vector<vector<int>>& matrix) 
    {
        int m = matrix.size();
        int n = matrix[0].size();
        vector<vector<int>> dp(m+1,vector<int>(n+2,INT_MAX));
        //初始化
        for(int i = 0;i<=n+1;i++)
        {
            dp[m][i] = 0;
        }
        for(int i = m-1;i>=0;i--)
        {
            for(int j = 1;j<=n;j++)
            {
                dp[i][j] = min(min(dp[i+1][j-1],dp[i+1][j]),dp[i+1][j+1]) + matrix[i][j-1];
            }
        }
        int ret = dp[0][1];
        for(int i = 2;i<=n;i++)
        {
            ret = min(ret,dp[0][i]);
        }
        return ret;
    }
};

九、最小路径和

1.链接

64. 最小路径和 - 力扣（LeetCode）

2.描述

3.思路

（1）状态表示

以[i][j]位置为结束，最小的路径和为dp[i][j]

（2）状态表示方程

dp[i][j] = min(dp[i-1][j],dp[i][j-1]) + grid[i][j]

（3）初始化

多加一行和一列的辅助行和辅助列，初始化为最大值，然后让dp[0][1] = 0,确保第一个左上角位置的路径值是正确的，最大值则是保证其他路径不会选择非法路径

（4）填表顺序

从左上角到右下角

（5）返回值

dp[m][n]

4.参考代码

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) 
    {
        int m = grid.size();
        int n = grid[0].size();
        vector<vector<int>> dp(m+1,vector<int>(n+1,INT_MAX));
        dp[0][1] = 0;
        for(int i = 1;i<=m;++i)
        {
            for(int j = 1;j<=n;j++)
            {
                dp[i][j] = min(dp[i-1][j],dp[i][j-1]) + grid[i-1][j-1];
            }
        }
        return dp[m][n];
    }
};

十、地下城游戏

1.链接

174. 地下城游戏 - 力扣（LeetCode）

2.描述

3.思路

（1）状态表示

根据题意，这里若是使用以[i][j]位置结束的思路，则不能保证后续路程可以走完，要采用另一种思路

dp[i][j] : 以[ i ][ j ]位置开始，走到最后所需要消耗的最小健康值

（2）状态表示方程

dp[i][j] = min( dp[i+1][j],dp[i][j+1] ) - dungeon[ i ][ j ]

我们可以认为，某个位置的点数如果是正数则就是回血，可以减少消耗，若是负数则加上增加了消耗，并且，还要考虑到消耗不能为负数，负数意味着有一个大血包，但勇士不能从0血以下开始走，当遇到大血包时，我们认为该点走到结尾的消耗为0

（3）初始化

我们需要辅助层去保证不越界的问题，dp起始位置是在末尾（右下角），为了不越界，我们需要给辅助层初始化为最大值，而为了让第一个dp填对，我们要让其相邻的其中一个为0（dp[i+1][j] =0）

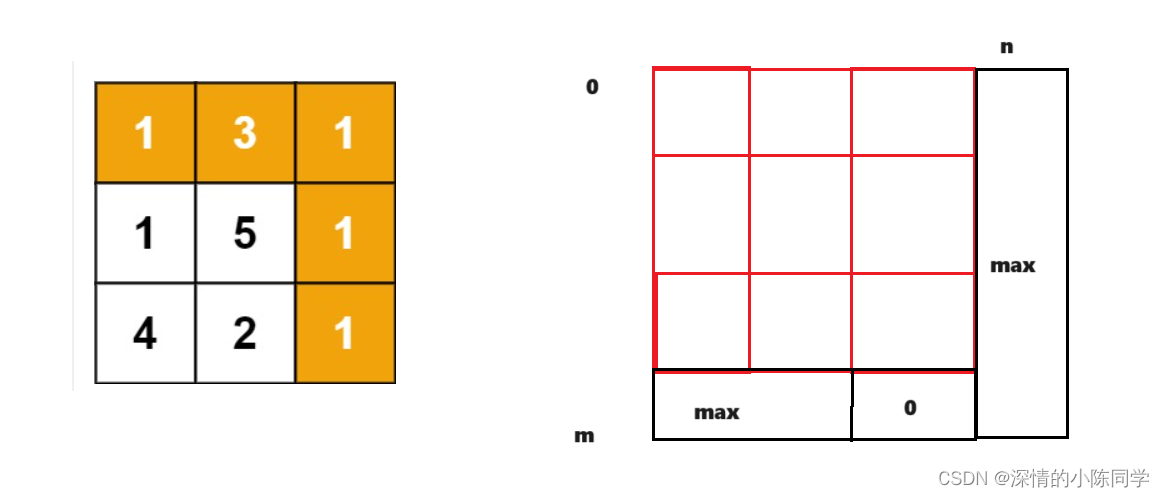
（4）填表顺序

从右下角开始，从右往左，从下往上

（5）返回值

return dp[0][0]+1;

4.参考代码

class Solution {
public:
    int calculateMinimumHP(vector<vector<int>>& dungeon) 
    {
        int m = dungeon.size();
        int n = dungeon[0].size();
        vector<vector<int>> dp(m+1,vector<int>(n+1,INT_MAX));
        dp[m][n-1] = 0;

        for(int i = m-1;i>=0;--i)
        {
            for(int j = n-1;j>=0;--j)
            {
                dp[i][j] = min(dp[i+1][j],dp[i][j+1]) - dungeon[i][j];
                dp[i][j] = max(0,dp[i][j]);
            }
        }
        return dp[0][0] + 1;
    }
};

总结

本篇总结了关于动态规划的一些题目，斐波那契数列类型的和路径问题相关的动态规划经典题目