题目链接
Leetcode.60 排列序列
题目描述
给出集合 [1,2,3,...,n],其所有元素共有
n
!
n!
n! 种排列。
按大小顺序列出所有排列情况,并一一标记,当 n = 3 n = 3 n=3 时, 所有排列如下:
"123"
"132"
"213"
"231"
"312"
"321"
给定 n 和 k,返回第 k 个排列。
示例 1:
输入:n = 3, k = 3
输出:“213”
示例 2:
输入:n = 4, k = 9
输出:“2314”
示例 3:
输入:n = 3, k = 1
输出:“123”
提示:
1 < = n < = 9 1 <= n <= 9 1<=n<=9
1 < = k < = n ! 1 <= k <= n! 1<=k<=n!
分析:
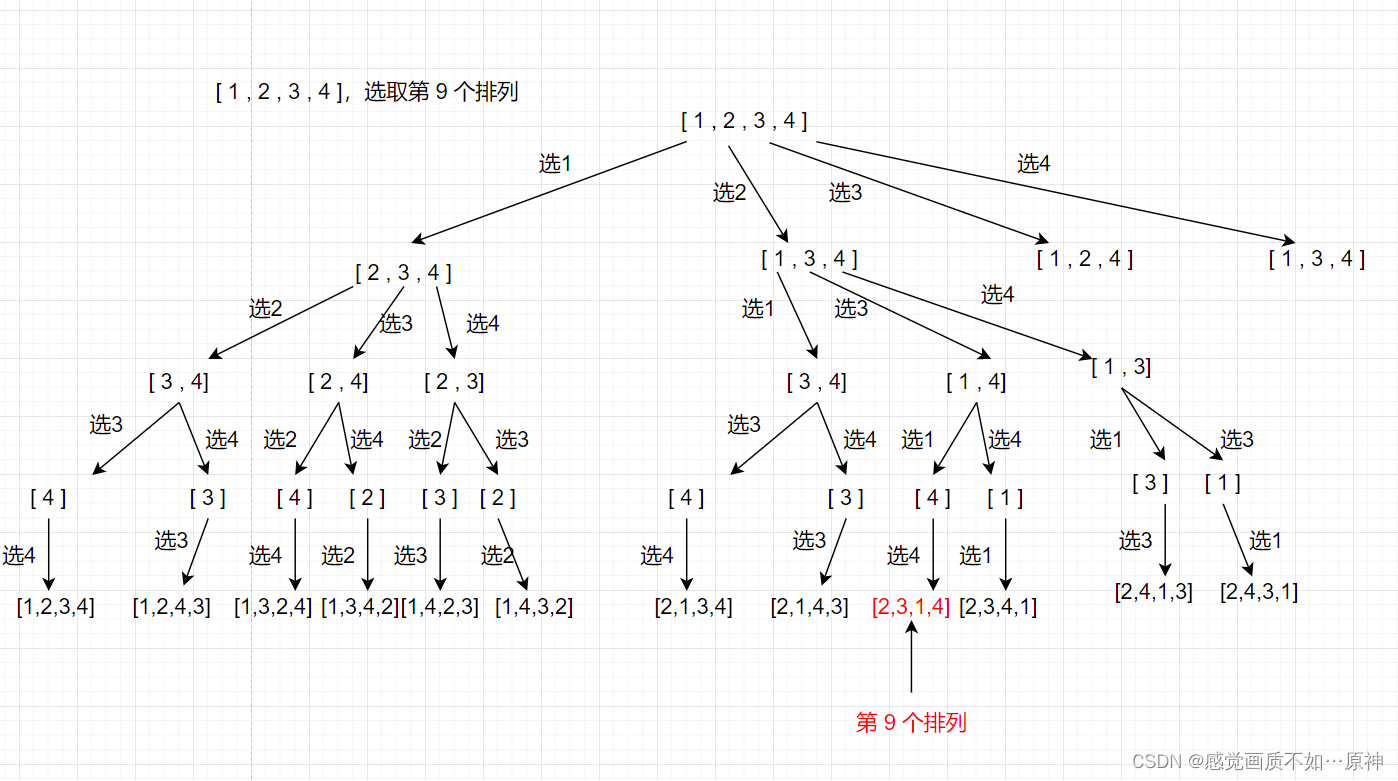
最容易想到的思路就是求出所有的排列,然后选取第 k 个排列返回即可,但是这个做法会超时,所以我们必须要剪枝。
剪枝的思路:当我们每次选取一个数时,可以用未选的数的个数 的阶乘
c
n
t
!
cnt!
cnt! 和 k 做判断。
- k < = c n t ! k <= cnt! k<=cnt! ,说明第 k 个排列就在这棵子树中,向下递归即可
- k > c n t ! k > cnt! k>cnt! , k − c n t ! k - cnt! k−cnt!, 说明第 k 个排列不在这棵子树中,我们就剪掉这棵子树(不向下递归了),即剪枝。
图示说明:
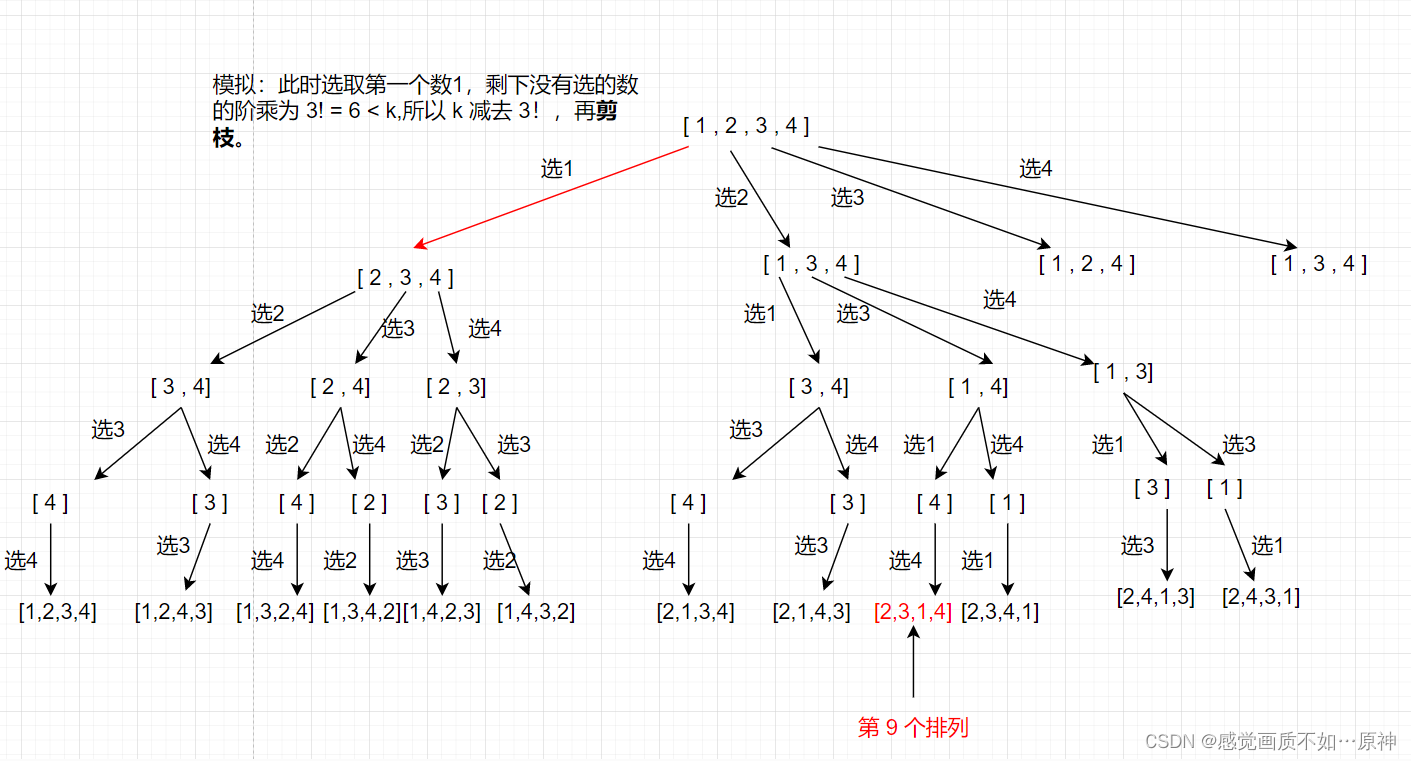
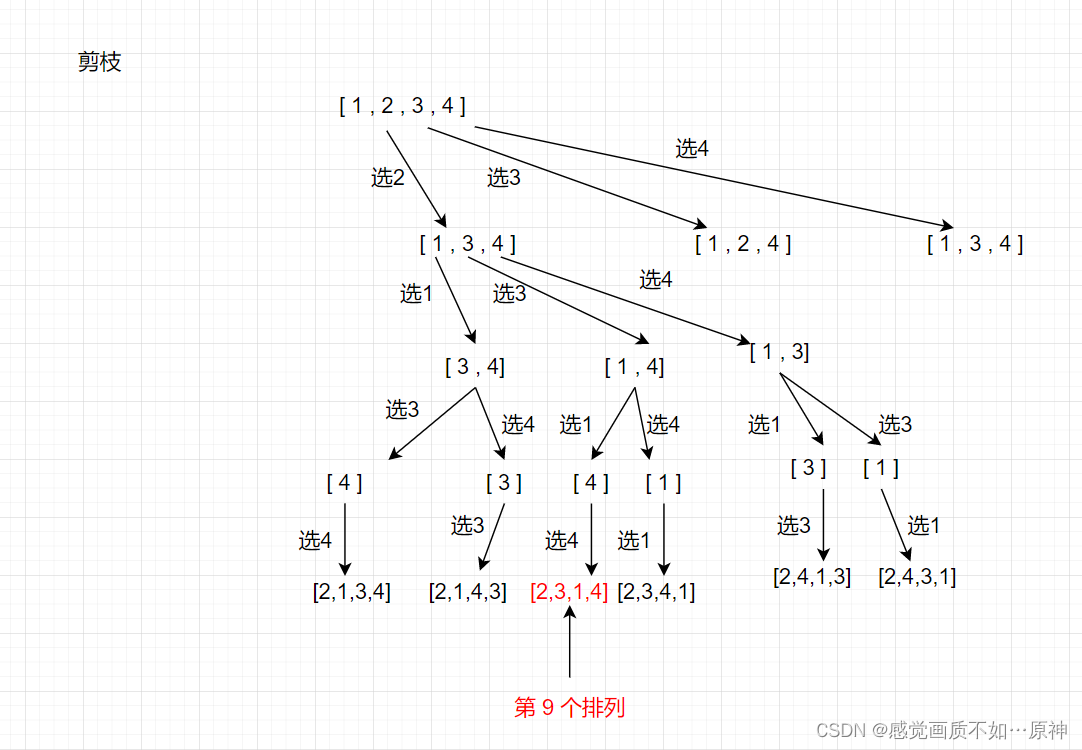
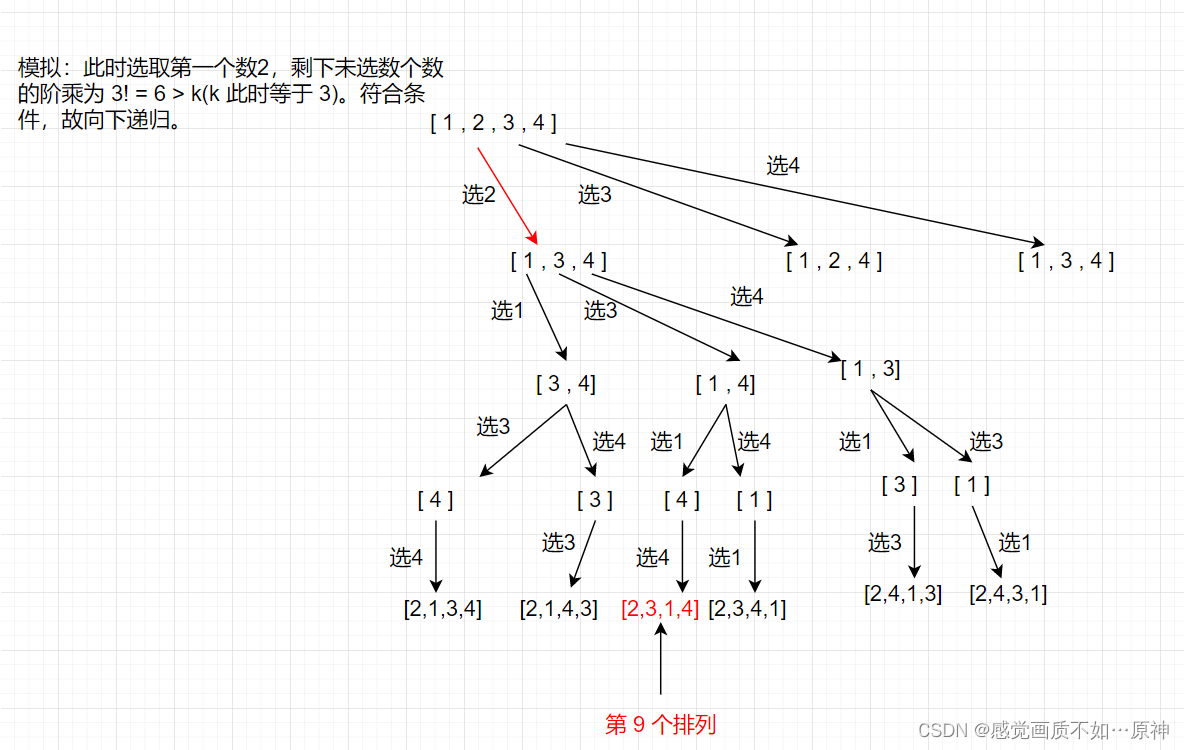
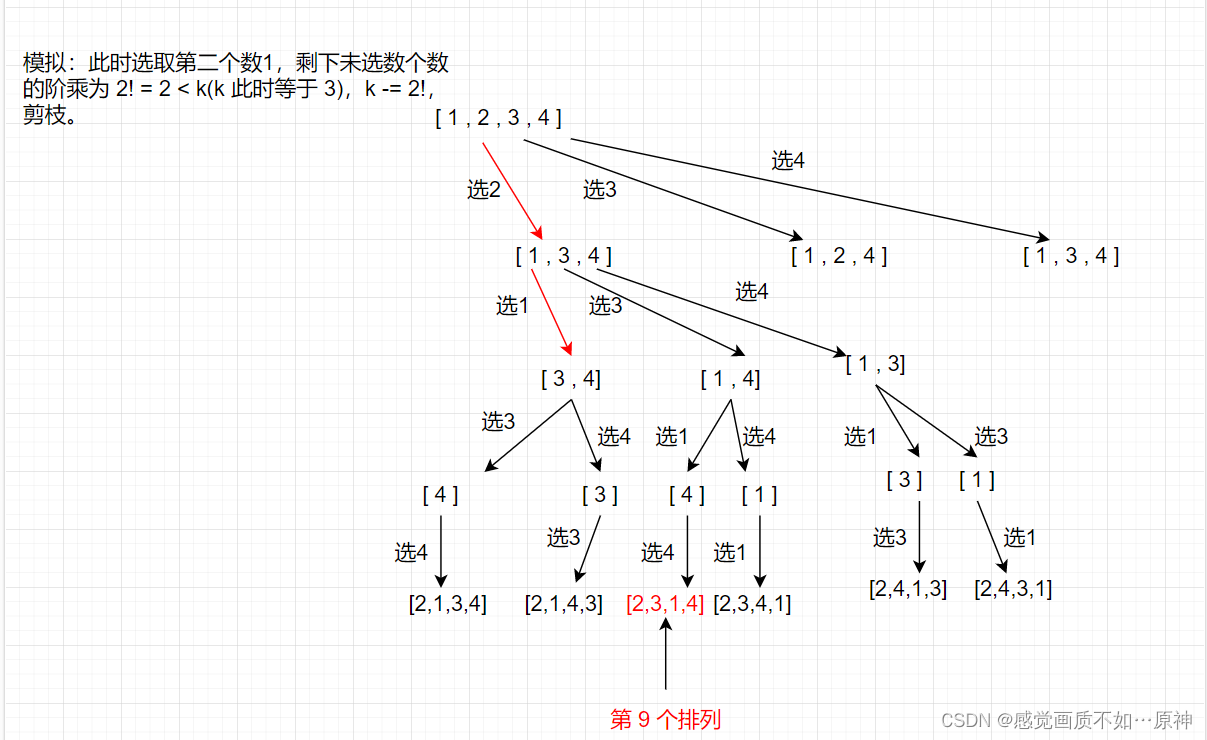
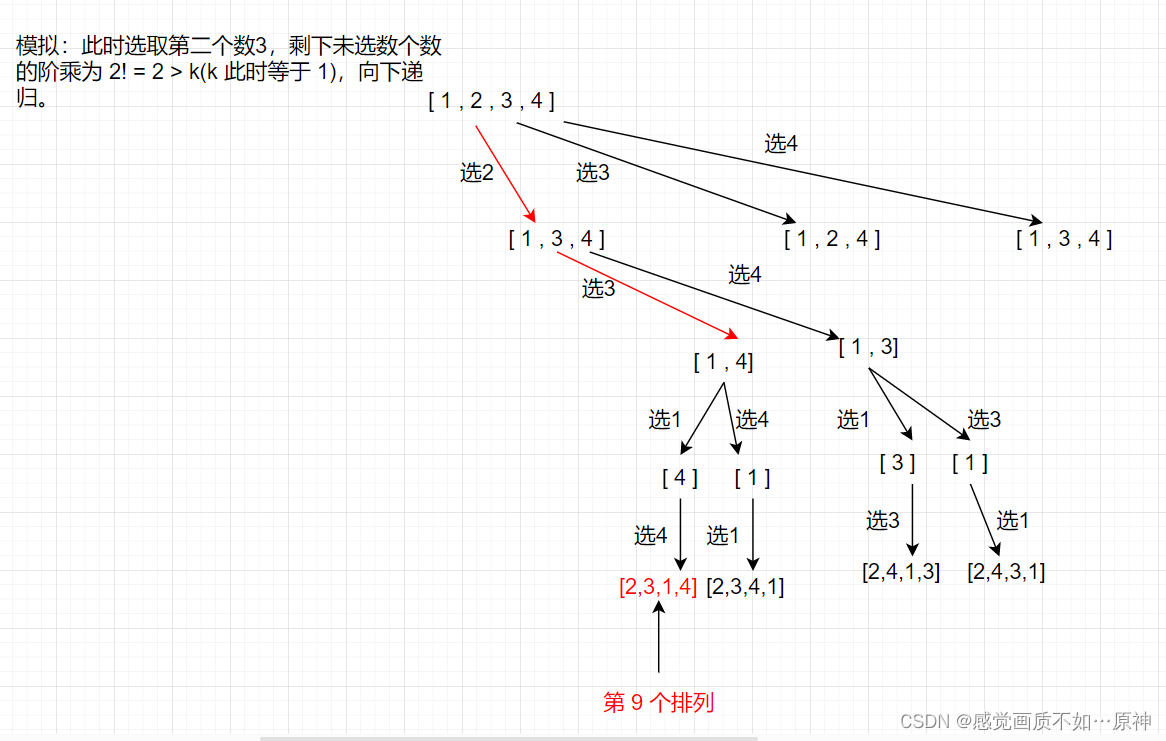
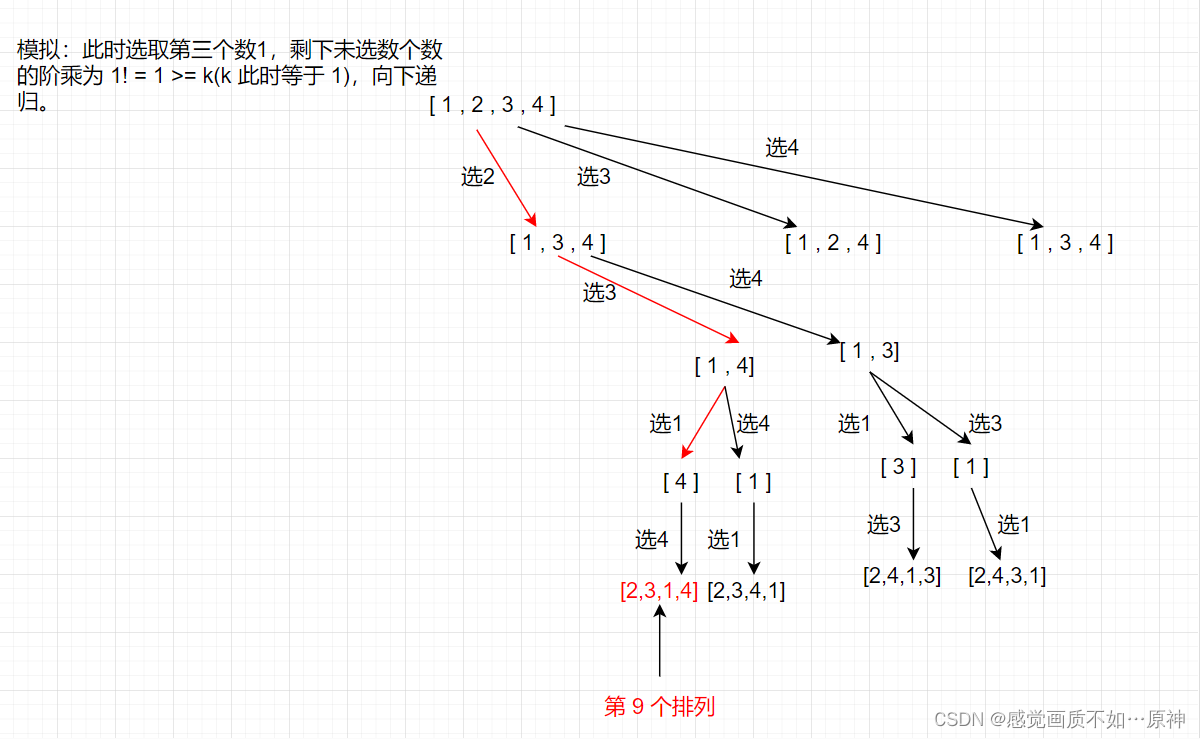
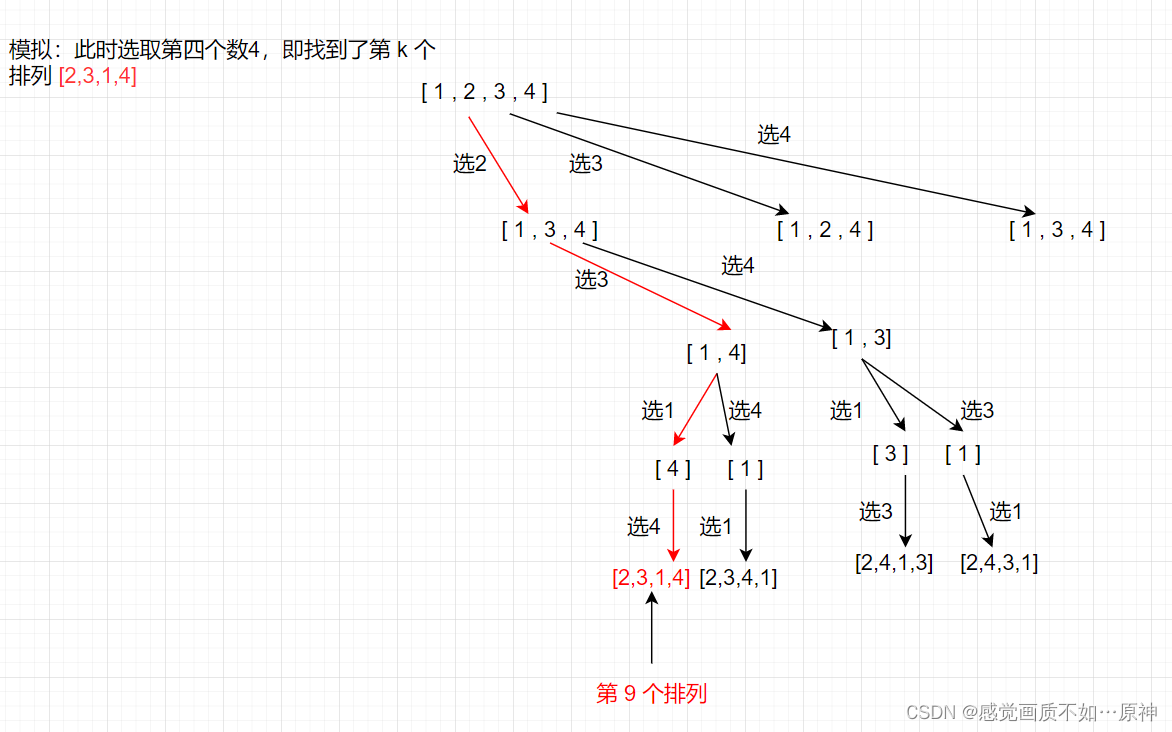
- 时间复杂度: O ( n 2 ) O(n^2) O(n2)
C++代码:
class Solution {
public:
int k,n;
int fun(int x){
int sum = 1;
while(x){
sum *= x;
x--;
}
return sum;
}
void permution(int u,string& s,vector<bool> vis){
if(u == n){
return;
}
int cnt = fun(n-u-1);
for(int i = 1;i <= n;i++){
if(vis[i]) continue;
if(cnt < k){
k -= cnt;
continue;
}
s += to_string(i);
vis[i] = true;
permution(u+1,s,vis);
return;
}
}
string getPermutation(int n, int k) {
vector<bool> vis(n+1);
this->k = k;
this->n = n;
string s = "";
permution(0,s,vis);
return s;
}
};
Java代码:
class Solution {
int n,k;
//阶乘数组 f[i] = i!
int[] f;
void fun(){
f[0] = 1;
for(int i = 1;i <= n;i++){
f[i] = i * f[i-1];
}
}
void dfs(int u,StringBuilder sb,boolean[] vis){
//当 u 等于 n时,说明已经找到了最终的第 k 个排列,直接返回即可
if(u == n) return;
//cnt 为剩下的没有被选的数 的个数的阶乘
int cnt = f[n - u - 1];
for(int i = 1;i <= n;i++){
//如果之前已经选了 i 这个数,就跳过本次循环
if(vis[i]) continue;
//如果 cnt < k 说明第 k 个排列不在这棵子树上,跳过本次循环,剪枝
if(cnt < k){
k -= cnt;
continue;
}
//由于我们要找的第 k 个排列是唯一的,所以不用回溯修改现场
vis[i] = true;
sb.append(i);
dfs(u+1,sb,vis);
//由于我们要找的路径只有一条,当回到本层循环的时候,说明已经找到了,此时再继续返回上一层就行
return;
}
}
public String getPermutation(int n, int k) {
this.n = n;
this.k = k;
this.f = new int[n+1];
fun();
StringBuilder sb = new StringBuilder();
boolean[] vis = new boolean[n+1];
dfs(0,sb,vis);
return sb.toString();
}
}