【题目来源】
https://www.acwing.com/problem/content/4612/

【题目描述】
给定 n 个火柴棍，你可以用它们摆出数字 0∼9。
摆出每个数字所需要的具体火柴棍数量如下图所示：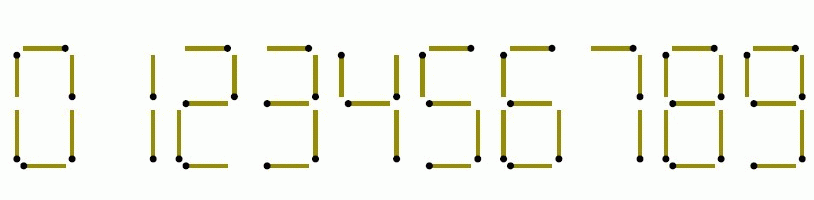

请你用这些火柴棍摆成若干个数字，并把这些数字排成一排组成一个整数，要求组成的整数尽可能大。
输出可以摆成的最大可能整数。

【输入格式】
第一行包含整数 T，表示共有 T 组测试数据。
每组数据占一行，包含一个整数 n。表示火柴根数。

【输出格式】
输出可以摆成的最大可能整数。

【数据范围】
前 3 个测试点满足 1≤t≤10。
所有测试点满足 1≤t≤100，2≤n≤10^5，同一测试点内所有 n 相加之和不超过 10^5。

【输入样例】
10
2
3
4
5
6
7
8
9
10
11

【输出样例】
1
7
11
71
111
711
1111
7111
11111
71111

【算法分析】
○ 给定的火柴棍数字中，凑出 1 需要 2 根火柴，凑出 7 需要 3 根火柴 ……
○ 位数越多的数，代表的数越大。
○ 而给定一个数，能凑出的最大位数为：
   若 n 为偶数，则最多能凑出 n/2 位，每位为 1；
   若 n 为奇数，依然能最多能凑出 n/2 位，其中最高位为 7，其他 n/2-1 位均为 1。

【算法代码】

#include <bits/stdc++.h>
using namespace std;

int main() {
    int T;
    cin>>T;
    while(T--) {
        int n;
        cin>>n;
        if(n%2==0) cout<<1;
        else cout<<7;

        for(int i=1; i<n/2; i++) cout<<1;
        cout<<endl;
    }
}


/*
in:
10
2
3
4
5
6
7
8
9
10
11

out:
1
7
11
71
111
711
1111
7111
11111
71111
*/

【参考文献】
https://www.acwing.com/video/4299/
https://www.acwing.com/solution/content/136165/