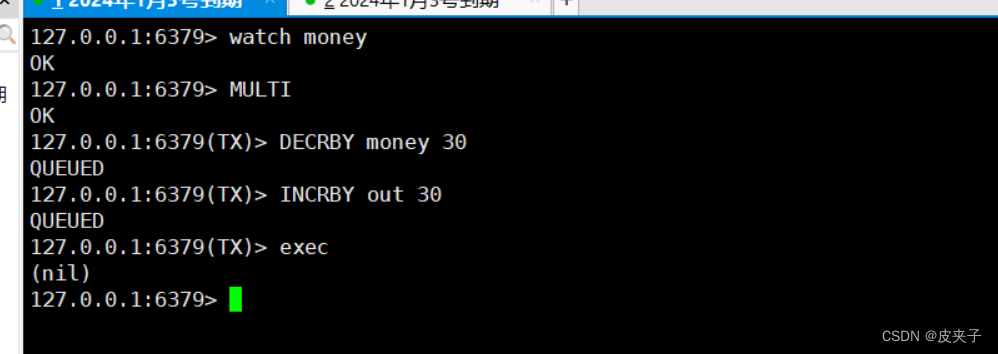
题意描述: 在算术表达式中,除了加、减、乘、除等运算外,往往还有括号。包括有大括号{},中括号[],小括号(),尖括号<>等。 对于每一对括号,必须先左边括号,然后右边括号;如果有多个括号,则每种类型的左括号和右括号的个数必须相等;对于多重括号的情形,按运算规则,从外到内的括号嵌套顺序为:大括号->中括号->小括号->尖括号。例如,{[()]},{()},{{}}为一个合法的表达式,而([{}]),{([])},[{<>}]都是非法的。
输入描述:
文件的第一行为一个整数n(1≤n≤100),接下来有n行仅由上述四类括号组成的括号表达式。第i+1行表示第i个表达式。每个括号表达式的长度不超过255。
输出描述:
在输出文件中有N行,其中第I行对应第I个表达式的合法性,合法输出YES,非法输出NO。
思路:1)运用栈来实现括号匹配,遍历字符串遇到括号就入栈,若匹配到右括号就将当前栈顶元素出栈,若右括号和当前栈顶元素不匹配或当前栈为空就返回错误。
2)每次进栈左括号前,检测栈是否为空,若不是,则判断当前栈顶元素括号是否优先级大于即将入栈元素,不是则返回错误
3)在遍历结束后,若栈为空,则匹配成功,括号合法。否则括号序列不匹配
#include <stdio.h>
#include <string.h>
//运用栈来实现括号匹配,遍历字符串遇到括号就入栈,若匹配到右括号就将当前栈顶元素出栈,若右括号和当前栈顶元素不匹配或当前栈为空就返回错误。
//每次进栈左括号前,检测栈是否为空,若不是,则判断当前栈顶元素括号是否优先级大于即将入栈元素,不是则返回错误
//在遍历结束后,若栈为空,则匹配成功,括号合法。否则括号序列不匹配
#define size 255
typedef struct stack{
char data[size];
int top;
}Stack;
//函数声明:
void init(Stack &a); //初始化栈顶指针
int push(Stack &a,int e); //入栈
int pop(Stack &a,char &e);//出栈
int is_empty(Stack a); //判断栈空
int judge(char s[],int length);
int judgeprior(char now,char before); //判断当前栈顶元素括号是否优先级大于即将入栈元素,优先级合法返回1,不合法返回0
int prior(char a);
int main(){
int n=0;
scanf("%d",&n);
getchar();
int result[255];
for(int i=0;i<n;i++)
{
char s[255];
gets(s);
int length=strlen(s);
int judgment=judge(s,length);
if(judgment==1)
result[i]=1;
else if(judgment==0)
result[i]=0;
}
for(int i=0;i<n;i++)
{
if(result[i])
printf("YES\n");
else printf("NO\n");
}
}
void init(Stack &a) //初始化栈顶指针
{
a.top=-1;
}
int push(Stack &a,int e) //入栈
{
if(a.top==size-1)
return -1;
a.top++;
a.data[a.top]=e;
return 1;
}
int pop(Stack &a,char &e){ //出栈
if(a.top==-1)
return -1;
e=a.data[a.top];
a.top--;
return 1;
}
int is_empty(Stack a) //判断栈空
{
if(a.top==-1)
return 1;
else return 0;
}
int judge(char s[],int length)
{
Stack a;
init(a);
for(int i=0;i<length;i++)
{
if(s[i]=='{'||s[i]=='['||s[i]=='('||s[i]=='<') //每次进栈左括号前,检测栈是否为空,若不是,则判断当前栈顶元素括号是否优先级大于即将入栈元素,不是则返回错误
{
if(is_empty(a))
push(a,s[i]);
else if(judgeprior(s[i],a.data[a.top]))
push(a,s[i]);
else return 0;
}
if(s[i]=='}'||s[i]==']'||s[i]==')'||s[i]=='>') //若匹配到右括号就将当前栈顶元素出栈,若右括号和当前栈顶元素不匹配或当前栈为空就返回错误。
{
if(is_empty(a))
return 0;
char e;
pop(a,e);
switch(s[i])
{
case '}':if(e=='{')
break;
else return 0;
case ']':if(e=='[')
break;
else return 0;
case ')':if(e=='(')
break;
else return 0;
case '>':if(e=='<')
break;
else return 0;
}
}
}
if(is_empty(a)) //在遍历结束后,若栈为空,则匹配成功,括号合法。否则括号序列不匹配
return 1;
else return 0;
}
int judgeprior(char now,char before){ //判断当前栈顶元素括号是否优先级大于即将入栈元素,优先级合法返回1,不合法返回0
int now_prior=prior(now);
int before_prior=prior(before);
if(now_prior<=before_prior)
return 1;
else return 0;
}
int prior(char a)
{
switch(a)
{
case '{': return 4;
case '[': return 3;
case '(': return 2;
case '<': return 1;
}
} 运行结果: