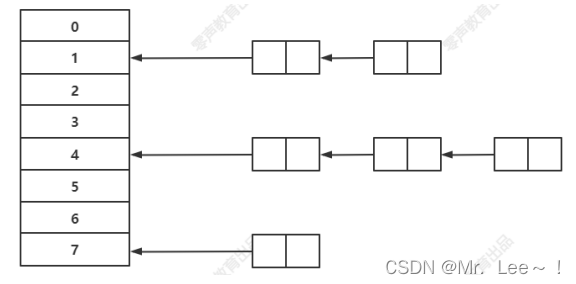
1. 散列表
- 根据 key 计算 key 在表中的位置的数据结构;是 key 和其所在存储地址的映射关系,即
hash(key) % size = index
struct node{
void *key;
void *value;
struct node *next;
};
2. hash函数
2.1 hash函数的特点
- 计算速度快
- 强随机分布性(等概率、均匀地分布在整个地址空间)
- 现有的hash函数:
- murmurhash1,murmurhash2,murmurhash3,其中1的速度最快但质量一般,3的质量最好但速度慢,2是两者均衡的也是使用最广泛的;
- siphash,在redis6.0当中使用,rust 等大多数语言都选用该hash算法来实现hashmap,主要解决字符串接近的强随机分布性;
- cityhash,与murmurhash是同一作者,也具备强随机分布性,是murmurhash的优化。
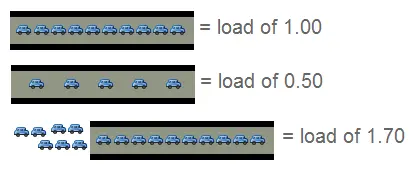
2.2 负载因子
- 负载因子 = 数组存储元素的个数 / 数组长度;
- 用来形容散列表的存储密度;负载因子越小,冲突概率越小,负载因子越大,冲突概率越大。
2.3 冲突处理
- 冲突处理的方法有两种不同的情况:一种情况是负载因子在合理范围内,即key的数量小于哈希数组的数量,这时候可以使用链表法或开放寻址法;另一种情况是负载因子不在合理范围内的情况
2.3.1 若负载因子在合理范围内
链表法
- 引用链表来处理哈希冲突;也就是将冲突元素用链表链接起来;
- 可能出现一种极端情况,冲突元素比较多,该冲突链表过长,这个时候可以将这个链表转换为红黑树、最小堆;由原来链表时间复杂度 O(n) 转换为红黑树时间复杂度 O(log n);
- 那么判断该链表过长的依据是多少?可以采用超过 256个节点的时候将链表结构转换为红黑树或堆结构(java hashmap);
开发寻址法
- 将所有的元素都存放在哈希表的数组中,不使用额外的数据结构;一般使用线性探查的思路解决;
- 步骤:
-
- 当插入新元素的时,使用哈希函数在哈希表中定位元素位置;
-
- 检查数组中该槽位索引是否存在元素。如果该槽位为空,则插入,否则进入步骤3;
-
- 在步骤2检测的槽位索引上加一定步长接着检查步骤2; 加一定步长分为以下几种:
- i+1, i+2, i+3, i+4, … , i+n
- i-1^2, i+2^2, i-3^2, i+4^2, …
- 这两种都会导致同类hash聚集;也就是近似值它的hash值也近似,那么它的数组槽位也靠近,形成 hash 聚集;第一种同类聚集冲突在前,第二种只是将聚集冲突延后; 另外还可以使用双重哈希来解决上面出现hash聚集现象:
-
2.3.2 负载因子不在合理范围内:
- 扩容:used > size 翻倍扩容
- 缩容:used < 0.1 * size
- rehash:由于size改变了,所以所有的key需要重新使用
hash(key) % size = index得到新的索引值
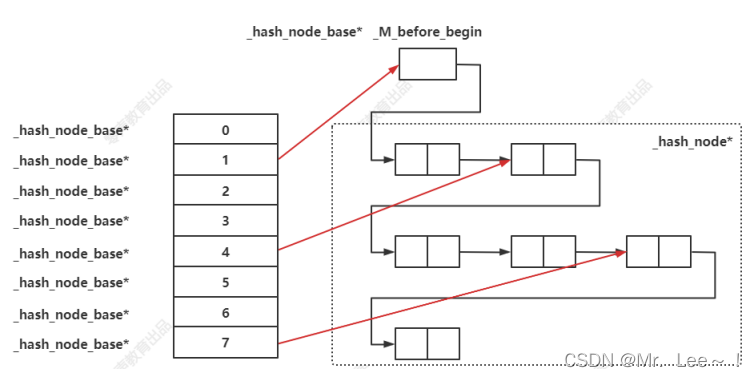
3. STL散列表实现
- unordered_set、unordered_map、unordered_multiset、unordered_multimap的底层实现都是使用hash
- 为了实现迭代器的顺序访问,将后面具体节点串成一个单链表
4. 布隆过滤器
-
背景:
- 布隆过滤器是一种概率型数据结构,它的特点是高效地插入和查询,能确定某个字符串一定不存在或者可能存在;
- 布隆过滤器不存储具体数据,所以占用空间小,查询结果存在误差,但是误差可控,同时不支持删除操作。
-
构成:
- 位图(BIT 数组)+ n 个 hash 函数
- m % 2^n = m & (2^n - 1)
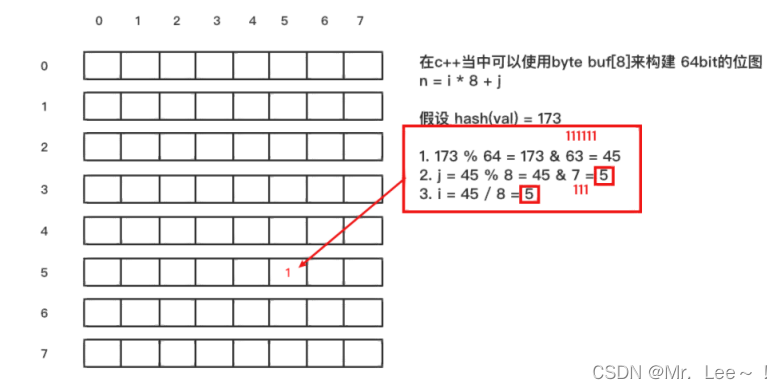
-
原理:
- 当一个元素加入位图时,通过 k 个 hash 函数将这个元素映射到位图的 k 个点,并把它们置为 1;当检索时,再通过 k 个 hash 函数运算检测位图的 k 个点是否都为 1;如果有不为 1 的点,那么认为该 key 不存在;如果全部为 1,则可能存在。
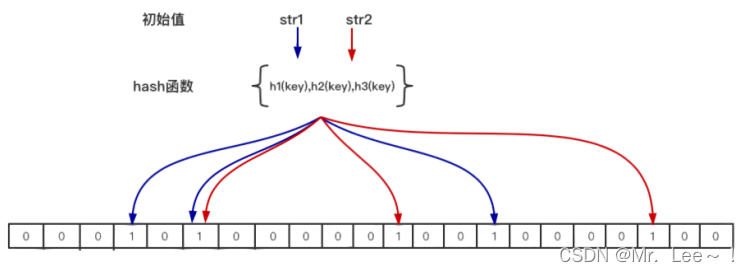
- 当一个元素加入位图时,通过 k 个 hash 函数将这个元素映射到位图的 k 个点,并把它们置为 1;当检索时,再通过 k 个 hash 函数运算检测位图的 k 个点是否都为 1;如果有不为 1 的点,那么认为该 key 不存在;如果全部为 1,则可能存在。
-
不支持删除操作:
- 在位图中每个槽位只有两种状态(0 或者 1),一个槽位被设置为 1 状态,但不确定它被设置了多少次;也就是不知道被多少个 key 哈希映射而来以及是被具体哪个 hash 函数映射而来。
-
根据n和p,算出m和k
- n: 预期布隆过滤器中元素的个数,如上图只有str1和str2 两个元素,那么 n=2
- p:假阳率,在0-1之间
- m:位图所占空间
- k:hash函数的个数
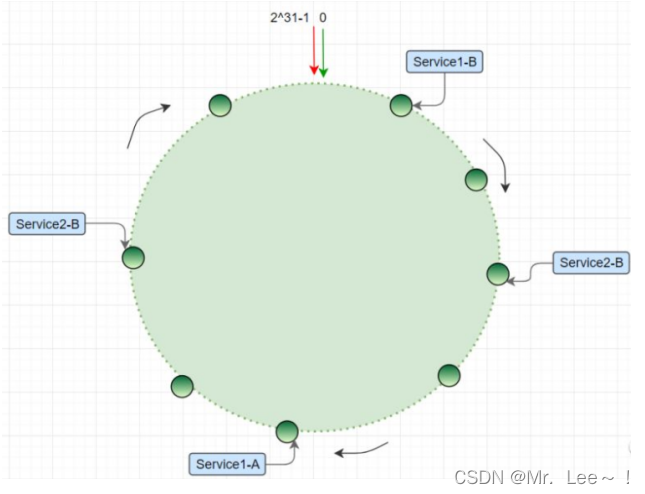
5. 分布式一致性hash
- 背景:
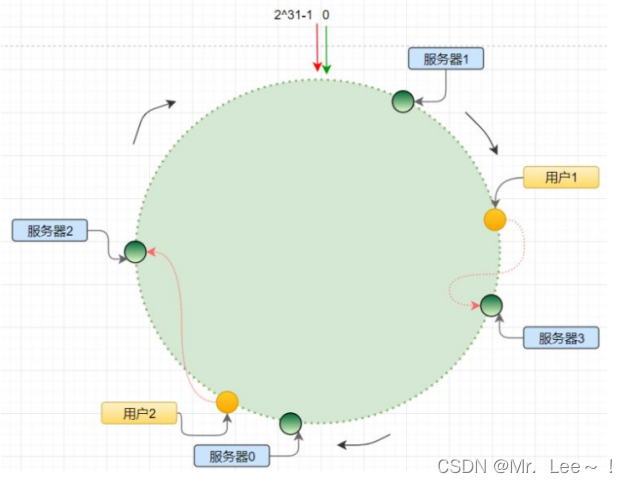
- 分布式一致性 hash 算法将哈希空间组织成一个虚拟的圆环,圆环的大小是 2^32;
hash(key) % bit_size = index- hash(ip) % 2^32,最终会得到一个 [0, 2^32 - 1] 之间的一个无符号整型,这个整数代表服务器的编号;多个服务器都通过这种方式在 hash 环上映射一个点来标识该服务器的位置;当用户操作某个 key,通过同样的算法生成一个值,沿环顺时针定位某个服务器,那么该 key 就在该服务器中。
- 解决了什么问题?
- 解决了分布式缓存扩容的问题
- 如何解决?
- 当服务器节点增加时,用户所存的服务器节点就会改变,这样就会导致全局缓冲失效
- 通过固定算法,即取余的值固定,为2^32,这样增加服务器节点时,全局缓存失效变成局部缓存失效,也就是增加节点的周围的用户缓存失效了
- 再通过数据迁移的方法,将失效用户的缓存迁移到正确的服务器节点,就可以避免局部缓存失效
- 通过加入虚拟节点,可以保证数据均衡