基础知识补充
完全二叉树:顺序存储(数组)
非根节点的父节点序号floor((i-1)/2)
序号i的左孩子节点序号2*i+1 右孩子节点序号2*i+2
一般二叉树:链式存储
结构:left指针指向左子节点,right指针指向右子节点,data存储数据项;
class TreeNode(object): def __init__(self, data, left=None, right=None): self.data = data self.left = left self.right= right平衡二叉树:左子树和右子树的高度之差的绝对值不超过1,且左子树和右子树也是平衡二叉树;
二叉搜索树:左子树上所有节点的值都小于根节点的值,右子树上所有节点的值都大于根节点的值,且左子树和右子树也是二叉搜索树
基础操作补充
1. 二叉树的插入
先判断父节点是否存在,再判断左子节点是否存在;构建右子节点后需要弹出父节点;
class BinTree(): def _init__(self): self.root = None self.ls =[] def add(self,data): node = TreeNode(data) if self.root == None: self.root = node self.ls.append(self.root) else: rootNode = self.ls[0] if rootNode.left == None: rootNode.left = node self.ls.append(rootNode.left) elif rootNode.right == None: rootNode.right = node self.ls.append(rootNode.right) self.ls.pop(0) #弹出子树已满的节点2. 二叉树的遍历
前序遍历(深度优先)当前节点-当前节点的左子树-当前节点的右子树 递归或栈实现
中序遍历(深度优先)当前节点的左子树-当前节点-当前节点的右子树 递归或栈实现
后序遍历(深度优先)当前节点的左子树-当前节点的右子树-当前节点 递归或栈实现
层序遍历(广度优先)各层级中从左到右的遍历 队列实现
已知两种二叉树遍历序列(其中需要包括中序遍历)可以唯一确定一棵二叉树;
#前序遍历的递归实现 def preOrderTraversal(self,root): if root == None: return print(root.data) self.preOrderTraversal(root.left) self.preOrderTraversal(root.right) #前序遍历的栈实现 def preOrderStack(self,root): if root == None:return stack =[] #存放节点 result =[] #存放节点值 node = root while node or stack: while node: result.append(node.data) stack.append(node) node = node.left node = stack.pop() node = node.right print(result) #中序遍历的递归实现 def inOrderTraversal(self,root): if root == None: return self.preOrderTraversal(root.left) print(root.data) self.preOrderTraversal(root.right) #中序遍历的栈实现 def inOrderStack(self,root): if root == None:return stack =[] #存放节点 result =[] #存放节点值 node = root while node or stack: while node: stack.append(node) node = node.left node = stack.pop() result.append(node.data) node = node.right print(result) #后序遍历的递归实现 def postOrderTraversal(self,root): if root == None: return self.preOrderTraversal(root.left) self.preOrderTraversal(root.right) print(root.data) #后序遍历的栈实现 def inOrderStack(self,root): if root == None:return stack =[] #存放节点 result =[] #存放节点值 seq = [] node = root while node or stack: #左-右-根视为根-右-左(前序的左右互换)的逆序 while node: seq.append(node.data) stack.append(node) node = node.right #内外层左右互换 node = stack.pop() node = node.left while seq: result.append(seq.pop()) #逆序 print(result) #层序遍历的队列实现 def levelOrder(seLf, root): if root == None:return queue =[] result =[] node = root queue.append(node) while queue: node = queue.pop(0) result.append(node.data) if node.left != None:queue.append(node.left) if node.right != None:queue.append(node.right) print(result)
题目
94 二叉树的中序遍历
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
方法一:递归实现
方法二:栈实现
class Solution(object): def inorderTraversal(self, root): """ :type root: TreeNode :rtype: List[int] """ if root == None: return stack = [] result = [] node = root while node or stack: while node: stack.append(node) node = node.left node = stack.pop() result.append(node.val) node = node.right return result方法三:颜色标记法:给每个节点一个访问状态,未访问为白,已访问为黑;
中序出栈顺序:左-中-右 对应的入栈顺序:右-中-左 栈:先进后出
class Solution(object): def inorderTraversal(self, root): """ :type root: TreeNode :rtype: List[int] """ white, black = 0, 1 result = [] stack = [(white, root)] while stack: color, node = stack.pop() if node is None:continue if color == white: stack.append((white, node.right)) stack.append((black, node)) stack.append((white, node.left)) # 适用于前中后序遍历,改变这里位置即可 else: result.append(node.val) return result方法四:莫里斯遍历
思路:如果左节点不为空,就将当前节点和右子树全部挂在左子树的最右子树下;
如果左节点为空,打印节点,并向右遍历;
class Solution(object): def inorderTraversal(self, root): """ :type root: TreeNode :rtype: List[int] """ res = [] pre = None while root: # 如果左节点不为空,就将当前节点连带右子树全部挂到左节点的最右子树下面 if root.left: pre = root.left while pre.right: pre = pre.right pre.right = root tmp = root root = root.left # 切换到左子树的父节点 tmp.left = None # 取消当前节点到左子树的链接 # 左子树为空,则打印这个节点,并向右边遍历 else: res.append(root.val) root = root.right return res
104 二叉树的最大深度
给定一个二叉树 root ,返回其最大深度。
方法一:二叉树最大深度 = max(左子树高度, 右子树高度)+1
class Solution(object): def maxDepth(self, root): """ :type root: TreeNode :rtype: int """ if root is None: return 0 else: left_height = self.maxDepth(root.left) right_height = self.maxDepth(root.right) return max(left_height, right_height) + 1方法二:用临时队列维护每层节点,一层结束后将深度+1
class Solution: def maxDepth(self, root): if not root: return 0 queue, res = [root], 0 while queue: tmp = [] for node in queue: if node.left: tmp.append(node.left) if node.right: tmp.append(node.right) queue = tmp res += 1 return res
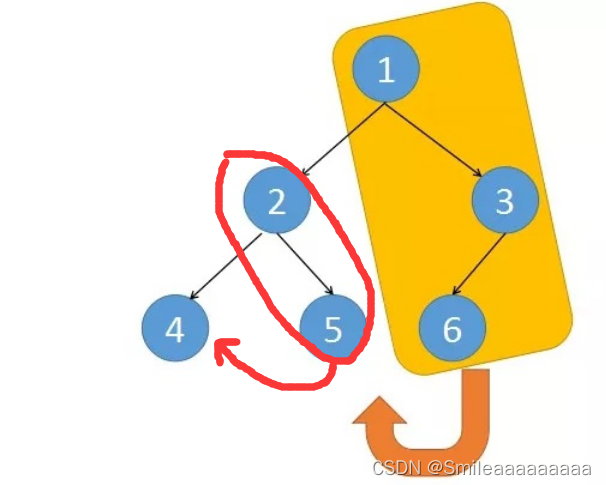
226 翻转二叉树
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
方法一:用栈做中序遍历:
class Solution(object): def invertTree(self, root): """ :type root: TreeNode :rtype: TreeNode """ stack = [] node = root while node or stack: while node: stack.append(node) node = node.left node = stack.pop() node.left, node.right = node.right, node.left node = node.left return root方法二:用队列做层级遍历
class Solution(object): def invertTree(self, root): """ :type root: TreeNode :rtype: TreeNode """ if root is None:return queue = [root] while queue: tmp = queue.pop(0) tmp.left,tmp.right = tmp.right,tmp.left if tmp.left:queue.append(tmp.left) if tmp.right:queue.append(tmp.right) return root方法三:递归实现
class Solution(object): def invertTree(self, root): """ :type root: TreeNode :rtype: TreeNode """ if root is None: return root.left,root.right = root.right,root.left self.invertTree(root.left) self.invertTree(root.right) return root
101 对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。
方法一:用队列做层级遍历,判断每层节点是否对称
class Solution(object): def invertTree(self, root): """ :type root: TreeNode :rtype: TreeNode """ quece = [root] while quece: tmp = [] val = [] for node in quece: if node.left: tmp.append(node.left) val.append(node.left.val) else:val.append(101) # 101是节点值范围之外的数 if node.right: tmp.append(node.right) val.append(node.right.val) else:val.append(101) if val != val[::-1]:return False # 耗时 quece = tmp return True # 不用滚动队列的话就一次性考虑两个节点,并在放置时将需要比较的节点相邻放置 class Solution(object): def isSymmetric(self, root): """ :type root: TreeNode :rtype: bool """ if not root or not (root.left or root.right):return True queue = [root.left,root.right] while queue: left = queue.pop(0) right = queue.pop(0) if not (left or right): # 两个节点都为空 continue if not (left and right): # 两个节点中有一个为空 return False if left.val!=right.val: # 两个节点的值不相等 return False queue.append(left.left) queue.append(right.right) queue.append(left.right) queue.append(right.left) return True方法二:递归实现
class Solution(object): def isSymmetric(self, root): """ :type root: TreeNode :rtype: bool """ if not root: return True def dfs(left,right): if not (left or right): # 两个节点都为空 return True if not (left and right): # 两个节点中有一个为空 return False if left.val!=right.val: # 两个节点的值不相等 return False return dfs(left.left,right.right) and dfs(left.right,right.left) return dfs(root.left,root.right)
543 二叉树的直径
给你一棵二叉树的根节点,返回该树的 直径 。二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。两节点之间路径的 长度 由它们之间边数表示。
分析:直径 = 左子树到父节点的最长路径 + 右子树到父节点的最长路径
左/右子树到父节点的最长路径 = 左/右子树深度
子树深度不用重复计算:height = max(左子树深度, 右子树深度)+1
方法一:使用全局变量
class Solution(object): def diameterOfBinaryTree(self, root): """ :type root: TreeNode :rtype: int """ global maxx maxx = 0 def depth(root): if root is None:return 0 left = depth(root.left) right = depth(root.right) global maxx maxx = max(maxx, left+right) return max(left, right)+1 depth(root) return maxx方法二:不使用全局变量
class Solution(object): def diameterOfBinaryTree(self, root): """ :type root: TreeNode :rtype: int """ depth, length = self.depth(root) return length def depth(self, root): if root is None:return (0, 0) left_depth, left_length = self.depth(root.left) right_depth, right_length = self.depth(root.right) depth = max(left_depth, right_depth) + 1 length = max(left_length, right_length, left_depth + right_depth) return depth, length
102 层序遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
方法一:两个数组实现
class Solution(object): def levelOrder(self, root): """ :type root: TreeNode :rtype: List[List[int]] """ if root is None:return [] quece, result = [root], [] while quece: tmp_res, tmp_que = [], [] while quece: node = quece.pop(0) tmp_res.append(node.val) if node.left:tmp_que.append(node.left) if node.right:tmp_que.append(node.right) result.append(tmp_res) quece = tmp_que return result方法二:一个数组实现,用变量确定每层需要处理的子节点数即可正常插入数组;
class Solution(object): def levelOrder(self, root): """ :type root: TreeNode :rtype: List[List[int]] """ if root is None:return [] quece, result = [root], [] while quece: length = len(quece) tmp_res = [] for i in range(length): node = quece.pop(0) tmp_res.append(node.val) if node.left:quece.append(node.left) if node.right:quece.append(node.right) result.append(tmp_res) return result
108 将有序数组转换为二叉搜索树
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵平衡二叉搜索树。
针对平衡,同时添加左子树和右子树;针对搜索,将数组确定父节点后进行二分;
递归实现
class Solution(object): def sortedArrayToBST(self, nums): """ :type nums: List[int] :rtype: TreeNode """ def balanceTree(left, right): if left > right: return None mid = (left+right)//2 root = TreeNode(nums[mid]) root.left = balanceTree(left, mid-1) root.right = balanceTree(mid+1, right) left, right = 0, len(nums)-1 return balanceTree(left, right)
98 验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
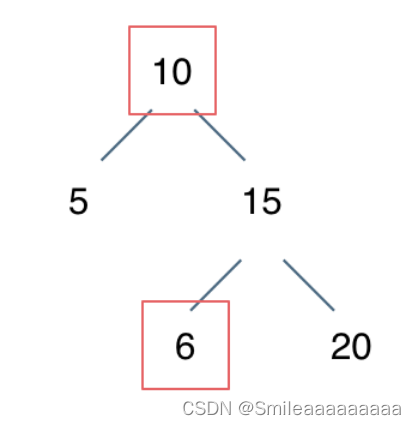
方法一:验证:左子节点值<父节点值<右子节点值 不够准确
在验证10的右子树时,首先所有值要大于10,即需要记录左右子树的不同边界值(左子树-上界 右子树-下界)
对于节点6来说,先在右子树确定下界为10,再在左子树确定上界为15,而6不属于这个区间;
class Solution(object): def isValidBST(self, root): """ :type root: TreeNode :rtype: bool """ def isBST(node, low, up): if node is None:return True if node.val<=low or node.val>=up: return False return isBST(node.left,low,node.val) and isBST(node.right,node.val,up) return isBST(root, -2**31-1, 2**31) # 题目范围的边界值方法二:利用"二叉搜索树的中序遍历一定升序排列"性质;
在构建中序遍历数组的同时可以进行升序比较;
230 二叉搜索树中第K小的元素
给定一个二叉搜索树的根节点 root ,和一个整数 k ,请你设计一个算法查找其中第 k 个最小元素(从 1 开始计数)。
利用"二叉搜索树的中序遍历一定升序排列"性质;构建中序遍历数组后直接取出第k个值即可;不构建中序遍历数组的话也可以选择对k处理(在需要插入值的位置将k减一,k归零时对应输出);
class Solution(object): def kthSmallest(self, root, k): """ :type root: TreeNode :type k: int :rtype: int """ stack = [] result = [] while root or stack: while root: stack.append(root) root = root.left root = stack.pop() result.append(root.val) root = root.right return result[k-1] class Solution: def kthSmallest(self, root, k): stack = [] while root or stack: while root: stack.append(root) root = root.left root = stack.pop() k -= 1 if k == 0: return root.val root = root.right
199 二叉树的右视图
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
返回层序遍历数组每层的最后一个值;
class Solution(object): def levelOrder(self, root): """ :type root: TreeNode :rtype: List[List[int]] """ if root is None:return [] quece, result = [root], [] while quece: length = len(quece) tmp_res = [] for i in range(length): node = quece.pop(0) tmp_res.append(node.val) # if i == length-1: result.append(node.val) if node.left:quece.append(node.left) if node.right:quece.append(node.right) result.append(tmp_res[-1]) return result
114. 二叉树展开为链表
给你二叉树的根结点 root ,请你将它展开为一个单链表:
- 展开后的单链表应该同样使用
TreeNode,其中right子指针指向链表中下一个结点,而左子指针始终为null。 - 展开后的单链表应该与二叉树 先序遍历 顺序相同。
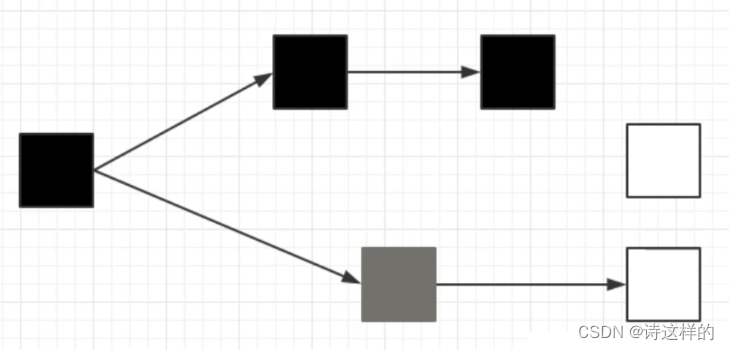
方法一:颜色标记法:出栈要求中-前-后,入栈则是右-前-中
需要创建虚拟链表头结点;
class Solution(object): def flatten(self, root): """ :type root: TreeNode :rtype: None Do not return anything, modify root in-place instead. """ white, black = 0, 1 stack = [(white, root)] head = TreeNode(0) pre_node = head while stack: color, node = stack.pop() if color == white: if node.right:stack.append((white, node.right)) if node.left:stack.append((white, node.left)) stack.append((black, node)) else: node.left = None pre_node.right = node pre_node = node return head.right方法二:找到链表的前置节点
对于当前节点,需要将其左子树的根节点移到右侧才能满足链表要求,而其右子树的根节点在链表中需要接在左子树最右结点之后。
class Solution(object): def flatten(self, root): """ :type root: TreeNode :rtype: None Do not return anything, modify root in-place instead. """ node = root while node: if node.left: left_node = left_last_node = node.left while left_last_node.right: left_last_node = left_last_node.right left_last_node.right = node.right node.left = None node.right = left_node node = node.right return root
105 从前序与中序遍历序列构造二叉树
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
前序遍历:中-左-右
中序遍历:左-中-右
前序遍历的第一个元素为根节点,在中序遍历序列找到根节点后就能将元素二分为左子树元素和右子树元素,再在前序遍历序列中找到左子树的根节点和右子树的根节点,...
class Solution(object): def buildTree(self, preorder, inorder): """ :type preorder: List[int] :type inorder: List[int] :rtype: TreeNode """ def bulidThree(preorder, inorder): if preorder: root = TreeNode(preorder[0]) idx = inorder.index(preorder[0]) inorder_left = inorder[:idx] inorder_right = inorder[idx+1:] preorder_left = preorder[1:idx+1] preorder_right = preorder[idx+1:] root.left = bulidThree(preorder_left, inorder_left) root.right = bulidThree(preorder_right, inorder_right) return root else:return return bulidThree(preorder, inorder)每次查找根节点坐标会造成时间浪费,可以用hashmap存储(空间换时间)
437 路径总和III
给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
统计从根节点出发到每个子节点的数值和,用不同节点的数值和做差得到截选的路径(类似前缀和想法)
需要在退出当前节点时更新前缀和(保证路径方向向下)
class Solution(object): def pathSum(self, root, targetSum): """ :type root: TreeNode :type targetSum: int :rtype: int """ global out cur_sum, out = 0, 0 hash = {0:1} # 初始化,不然根节点与目标值相等时只能插入hash def partSum(root, targetSum, hash, cur_sum): if root is None: return 0 global out cur_sum += root.val if targetSum - cur_sum in hash: out += hash[targetSum-cur_sum] if cur_sum in hash:hash[cur_sum] += 1 # 有正有负,会出现重复的前缀和 else:hash[cur_sum] = 1 partSum(root.left, targetSum, hash, cur_sum) partSum(root.right, targetSum, hash, cur_sum) hash[cur_sum] -= 1 cur_sum -= root.val partSum(root, targetSum, hash, cur_sum) return out
236 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
对于当前节点,若能从其左子树中找到p/q并从其右子树中找到q/p,则该节点为最近公共祖先节点;
若左侧无p/q,则pq均在右子树,将当前节点切换到当前右子节点;
终止条件:切换到叶子节点或找到p/q;
class Solution(object): def lowestCommonAncestor(self, root, p, q): """ :type root: TreeNode :type p: TreeNode :type q: TreeNode :rtype: TreeNode """ if root==p or root==q or root==None: return root left=self.lowestCommonAncestor(root.left,p,q) right=self.lowestCommonAncestor(root.right,p,q) if left and right:return root if left and right==None:return left if right and left==None:return right
124 二叉树的最大路径和
二叉树中的 路径 被定义为一条节点序列,序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。路径和 是路径中各节点值的总和。给你一个二叉树的根节点 root ,返回其 最大路径和 。
和543相似的思路,只是不再记录深度而是路径和;
class Solution(object): def maxPathSum(self, root): """ :type root: TreeNode :rtype: int """ global max_sum max_sum = -1001 # 题目给出的节点的值的下界 def partPathSum(root): if root is None:return 0 left = partPathSum(root.left) left = max(left, 0) # 除去负值 right = partPathSum(root.right) right = max(right, 0) global max_sum max_sum = max(max_sum, root.val+left+right) return root.val+max(left, right) partPathSum(root) return max_sum