labuladong回溯
回溯算法秒杀所有排列-组合-子集问题

回溯

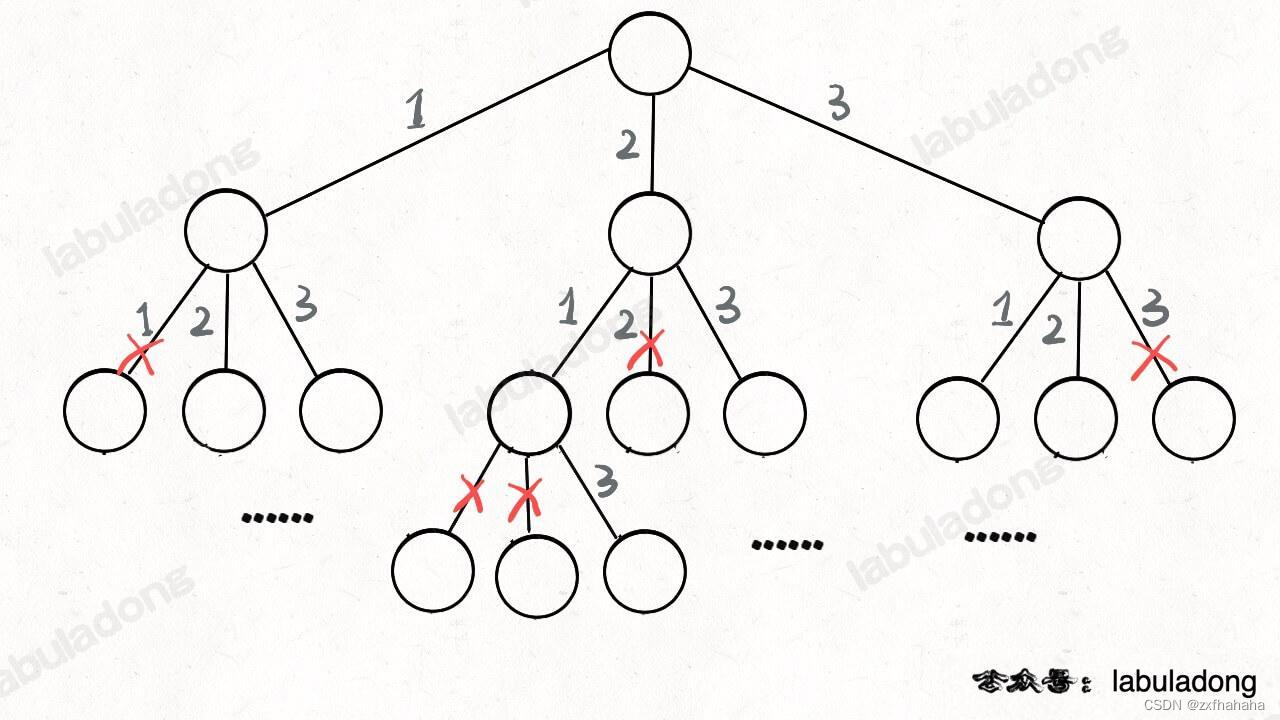
一个回溯问题，实际上就是遍历一棵决策树的过程，树的每个叶子节点存放着一个合法答案。你把整棵树遍历一遍，把叶子节点上的答案都收集起来，就能得到所有的合法答案。
站在回溯树的一个节点上，你只需要思考 3 个问题：
1、路径：也就是已经做出的选择。
2、选择列表：也就是你当前可以做的选择。
主要就是在选择前先把不能选的排除调，比如全排列是要排除掉已经选了的数字，n皇后是要把当前列，左上角斜线和右上角斜线 有皇后的排除掉。
3、结束条件：也就是到达决策树底层，无法再做选择的条件。
这里add到res的时候要new 一个新的list

模板

写 backtrack 函数时，需要维护走过的「路径」和当前可以做的「选择列表」，当触发「结束条件」时，将「路径」记入结果集。

回溯就是核心就是 for 循环里面的递归，在递归调用之前「做选择」，在递归调用之后「撤销选择」.

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return
    
    for 选择 in 选择列表:
    	1. 排除不合法选择
        2. 做选择
        3. backtrack(路径, 选择列表)
        4. 撤销选择

例题

46.全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2：
输入：nums = [0,1]
输出：[[0,1],[1,0]]
示例 3：
输入：nums = [1]
输出：[[1]]
提示：

1 <= nums.length <= 6
-10 <= nums[i] <= 10
nums 中的所有整数 互不相同

---

选择列表其实就是 nums除去已经选过的数，所以我们可以用int[] used 记录被选的数

class Solution {

    List<List<Integer>> res = new LinkedList<>();

    public List<List<Integer>> permute(int[] nums) {

        LinkedList<Integer> track = new LinkedList<>();
        // 初始值都是false
        boolean[] used = new boolean[nums.length];
        backtrack(nums, track, used);
        return res;
    }

    private void backtrack(int[] nums, LinkedList<Integer> track, boolean[] used){
        // 到叶子节点
        if (track.size()==nums.length){
            res.add(new LinkedList(track));
            return ;
        }
        for (int i=0;i<nums.length;i++){
            // 排除不合法选择
            if (used[i]){
                continue;
            }
            // 做出选择
            track.add(nums[i]);
            used[i] = true;
            // 下一层决策树
            backtrack(nums, track, used);
            // 撤回选择
            track.removeLast();
            used[i] = false;
        }
    }
}

51. n皇后

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
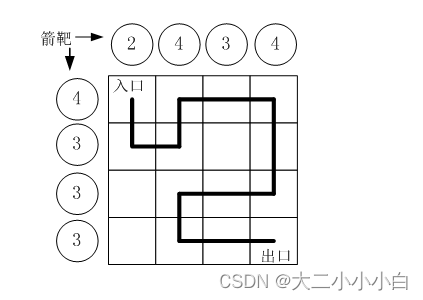
输入：n = 4
输出：[[“.Q…”,“…Q”,“Q…”,“…Q.”],[“…Q.”,“Q…”,“…Q”,“.Q…”]]
解释：如上图所示，4 皇后问题存在两个不同的解法。
示例 2：

输入：n = 1
输出：[[“Q”]]

---

这道题其实就是遍历棋盘上的每一行，当所有行都遍历完了 就是放遍历到的路径的时候。
做选择的时候要把当前位置不能放皇后的排除掉，排除的方法就是看当前列，左上角斜线，右上角斜线有没有皇后。

class Solution {
    List<List<String>> res = new LinkedList<>();
    public List<List<String>> solveNQueens(int n) {
        // 初始化棋盘
        List<String> board = new LinkedList<>();
        for (int i=0;i<n;i++){
            StringBuilder sb = new StringBuilder();
            for (int j=0;j<n;j++){
                sb.append(".");
            }
            board.add(sb.toString());
        }
        backtrack(board, 0);
        return res;
    }

    // 一行的选择其实就是 决策树的一层

    private void backtrack(List<String> board, int row){
        // 结束条件 最后一行遍历完是board.size()-1，最后一行的下一行就应该结束了
        if (board.size()==row){
            res.add(new LinkedList(board));
            return ;
        }

        int n = board.get(row).length();
        for (int col=0;col<n;col++){
            // 排除不合法选择
            if (!isValid(board, row, col)){
                continue;
            }
            // 做出选择：也就是把皇后Q放到当前col
            StringBuilder sb = new StringBuilder(board.get(row));
            sb.setCharAt(col, 'Q');
            board.set(row, sb.toString());

            // 去遍历下一层
            backtrack(board, row+1);
            // 撤销选择
            sb.setCharAt(col, '.');
            board.set(row, sb.toString());

        }
    }

    private boolean isValid(List<String> board, int row, int col){
        int n = board.size();
        // 看每一行的当前列 是否有皇后
        for (int i = 0; i < n; i++) {
            if (board.get(i).charAt(col)=='Q'){
                return false;
            }
        }
        // 看左上方 斜线是否有皇后
        for (int i=row-1,j=col-1;i>=0&& j>=0;i--,j--){
            if (board.get(i).charAt(j)=='Q'){
                return false;
            }
        }

        /* 检查右上方是否有皇后互相冲突 */
        for (int i = row - 1, j = col + 1;
             i >= 0 && j < n; i--, j++) {
            if (board.get(i).charAt(j) == 'Q') {
                return false;
            }
        }
        return true;
    }
}

52. n皇后 ②

n 皇后问题 研究的是如何将 n 个皇后放置在 n × n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回 n 皇后问题 不同的解决方案的数量。

---

和51其实一样，只是存结果的时候不用存了，只用加数量即可

	int res = 0;

    private void backtrack(List<String> board, int row){
        // 结束条件 最后一行遍历完是board.size()-1，最后一行的下一行就应该结束了
        if (board.size()==row){
            res++;
            return ;
        }